一种基于有限域乘群中循环子群生成元的LDPC码构造方法与流程

本发明涉及LDPC码构造技术领域，更具体涉及一种基于有限域乘群中循环子群生成元的LDPC码构造方法。

背景技术：

在20世纪50年代后期、60年代初，有限域成功用来构造线性分组码，这些码对于硬判决译码算法具有较大的最小码间距离，其中的代表如BCH码、RS码。2001年，林舒教授将有限域构造引入到LDPC码的构造中，产生了一类新的具有大的最小距离、良好收敛特性和低差错平底的一类LDPC码。

LDPC码由其稀疏的奇偶校验矩阵H唯一确定。若H具有恒定的列重γ，行重ρ，则其对应的LDPC码称为规则LDPC码，否则，称为不规则LDPC码。一个设计良好的LDPC码结合基于置信度传播的迭代译码算法在AWGN信道条件下误比特率曲线能够十分接近香农限。而研究表明，校验矩阵中的短环，特别是长度为4的环，在置信度传播的过程中破坏了信息间的独立性，阻止迭代译码算法的收敛，会导致较差的误比特率性能和较高的差错平底，因此，几乎在所有的码构造中，下面的约束总是被提及：校验矩阵中的任意两行不存在两个或更多的位置同时存在非零元，这条约束被称作行列约束。若校验矩阵满足此约束，且其最小列重为γmin，则其最小码间距离为γmin+1，该下界在γmin较大时比较紧。

若校验矩阵为稀疏的分块循环矩阵，则其零空间给出一个准循环LDPC码。准循环LDPC码的优势体现在硬件实现中，编码可以通过循环移位寄存器实现，实现复杂度与码字长度或校验位长度呈线性关系；在译码器的硬件实现中，准循环的LDPC码在布线中具有优势，而且准循环结构可以采用准并行的架构，这在译码器的速度和复杂度间提供了折中。由此可见，准循环的LDPC码是LDPC码中重要的一类。

与此相对的随机或伪随机LDPC码由于校验矩阵在结构上不具有如循环或准循环的特性，使得编码和译码实现变得十分复杂。

技术实现要素：

(一)要解决的技术问题

本发明要解决的技术问题是如何构造一种性能优异的LDPC码，兼有准循环LDPC码或循环LDPC码在编译码实现中的优势与随机或伪随机LDPC码的优异的误码性能。

(二)技术方案

为了解决上述技术问题，本发明提供了一种基于有限域乘群中循环子群生成元的LDPC码构造方法，所述方法包括以下步骤：

S1、确定码参数，即码长L和码率R的范围，根据所述码参数确定码构造的有限域GF(q)，所述有限域GF(q)所能构造的码字最大长度大于所述码长L，其中q表示所述有限域中元素的数量；q-1不是质数，并分解为互质的两个因子的乘积，即q-1＝c×n；

S2、确定所述有限域上乘群的两个循环子群，即和其中δ＝αⁿ、β＝α^c，则δ和β分别具有阶数c和n，并且满足α为所述有限域GF(q)的本原元；

S3、确定所述两个循环子群的全部生成元；具体为：

对于所述循环子群如果有1≤a＜c，并且a与c的最大公约数为1，则δ的a次方为的生成元；根据上述方法求取循环子群的全部生成元，所述生成元的数量为Kc，所述循环子群的全部生成元表示为其中v0＝0；

对于所述循环子群如果有1≤b＜c，并且b与n的最大公约数为1，则β的b次方为的生成元，根据上述方法求取循环子群的全部生成元，所述生成元的数量为Kn，所述循环子群设的全部生成元表示为其中u0＝0；

S4、根据所述步骤S3得到的全部生成元，构造(Kc+1)×(Kc+1)分块的基矩阵W，如公式(1)，每个子矩阵为(Kn+1)×(Kn+1)的矩阵，如公式(2)：

所述子矩阵Wi，j，0≤i≤Kc，0≤j≤Kc为：

所述基矩阵W的第i行分块第j列分块中的第s行第t列的元素等于所述循环子群中的第j个生成元除以第i个生成元乘上循环子群中的第t个生成元除以第s个生成元，然后减一，其中0≤i，j≤Kc、0≤s，t≤Kn，且循环子群和循环子群的第0个生成元均为1；

S5、根据步骤S4得到的基矩阵，将其的非零元扩展成(q-1)×(q-1)的循环置换矩阵，或广义循环置换矩阵，将所述基矩阵的零元扩展成(q-1)×(q-1)的零矩阵；得到如公式(3)形式的(Kc+1)(Kn+1)×(Kc+1)(Kn+1)的分块矩阵，即扩展矩阵H：

S6、选取所述扩展矩阵H的子矩阵H(γ，ρ)做校验矩阵，H(γ，ρ)的零空间给出所要构造的准循环LDPC码，具体为：

根据所述码长和码率的范围确定子矩阵的行分块数γ和列分块数ρ，其中所述列分块数ρ的取值使ρ(q-1)的值接近或等于要码长L；所述行分块数γ的取值使所要构造的校验矩阵的秩K接近或等于(1-R)ρ(q-1)的值；

从所述扩张矩阵H中选择连续的或者不连续的γ个行分块、ρ个列分块作为校验矩阵；若进一步要求校验矩阵中不含有全零子矩阵时，校验矩阵H(γ，ρ)选取要避开所述矩阵H中的零矩阵，即在主分块对角线上方或下方取值。

优选地，所述步骤S5具体为：

如果进行二元LDPC码的构造，则将所述基矩阵W中的非零元扩展成为二元的(q-1)×(q-1)循环置换矩阵，将所述基矩阵W中的零元扩展成为(q-1)×(q-1)零矩阵，得到一个二元的(q-1)×(q-1)分块校验矩阵H，其子矩阵为(q-1)×(q-1)的循环置换矩阵和零矩阵；

如果进行多元LDPC码的构造，即二元以上LDPC码的构建，则将所述基矩阵W中的非零元扩展成为多元的(q-1)×(q-1)的广义循环置换矩阵，将W中的零元扩展成为(q-1)×(q-1)零矩阵，得到一个多元的(q-1)×(q-1)分块校验矩阵H，其子矩阵为(q-1)×(q-1)的广义循环置换矩阵和零矩阵。

优选地，所述二元LDPC码的构造，非零元与扩展后的二元循环置换矩阵存在如下对应关系：

W中的所有非零元均表示为本原元α的幂次方的形式，即αⁱ，0≤i＜q-1；与元素αⁱ对应的循环置换矩阵为i次循环右移后的q-1维标准阵。

优选地，所述多元LDPC码的构造，非零元与扩展后的广义循环置换矩阵存在如下对应关系：

W中的所有非零元均表示为本原元α的幂次方的形式，即αⁱ，0≤i＜q-1；定义q-1维广义标准矩阵为主对角线上的元素为(α⁰，α¹，...，α^q-2)，其余元素均为0；与元素αⁱ对应的广义循环置换矩阵为q-1维广义标准矩阵i次循环右移后所有元素乘以αⁱ的q-1维广义标准阵，其中，α的幂取模q-1。

(三)有益效果

本发明提供了一种基于有限域乘群中循环子群生成元的LDPC码构造方法，该方法能够实现兼具有优异的误码性能和线性编译码复杂度的LDPC码的构造。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明的一种基于有限域乘群中循环子群生成元的LDPC码构造方法的流程图；

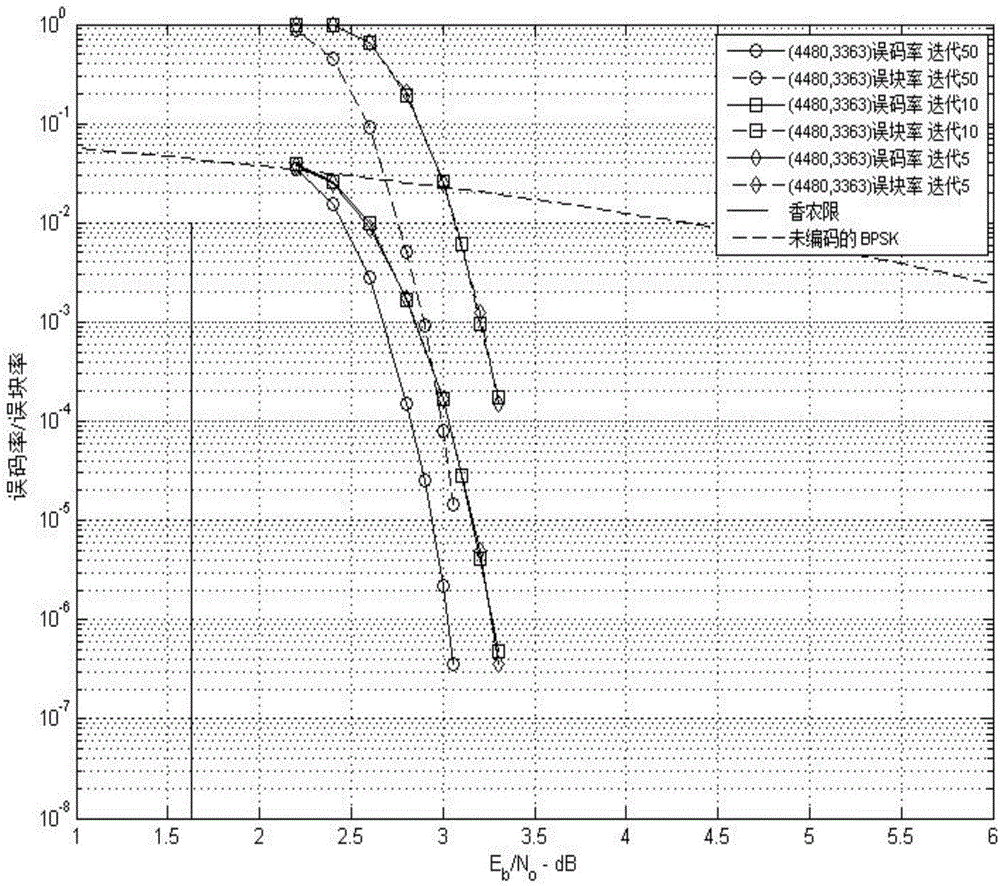
图2为利用本发明的方法所构造的两个(4080,3363)QC-LDPC码在AWGN信道条件下分别利用50次、10次、5次最大迭代次数的迭代译码算法得到的误码性能示意图。

具体实施方式

下面结合附图和实施例对本发明作进一步详细描述。以下实施例用于说明本发明，但不能用来限制本发明的范围。

图1为本发明的一种基于有限域乘群中循环子群生成元的LDPC码构造方法的流程图；一所述方法包括以下步骤：

S1、确定码参数，即码长L和码率R的范围，根据所述码参数确定码构造的有限域GF(q)，所述有限域GF(q)所能构造的码字最大长度大于所述码长L，其中q表示所述有限域中元素的数量；q-1不是质数，并分解为互质的两个因子的乘积，即q-1＝c×n；

所述有限域所构造出的LDPC码的最长的码长(Kc+1)(Kn+1)(q-1)大于所要构造码字的长度，即码长L，如果进一步要求构造的校验矩阵中不存在全零矩阵，则要使Mc+Nc≤(Kc+1)(Kn+1)，其中，Mc是分块校验矩阵的行分块数，Nc是分块校验矩阵的列分块数；

S2、确定所述有限域上乘群的两个循环子群，即和其中δ＝αⁿ、β＝α^c，则δ和β分别具有阶数c和n，并且满足α为所述有限域GF(q)的本原元；

S3、确定所述两个循环子群的全部生成元；具体为：

对于所述循环子群如果有1≤a＜c，并且a与c的最大公约数为1，则δ的a次方为的生成元；根据上述方法求取循环子群的全部生成元，所述生成元的数量为Kc，所述循环子群的全部生成元表示为其中v0＝0；

对于所述循环子群如果有1≤b＜c，并且b与n的最大公约数为1，则β的b次方为的生成元，根据上述方法求取循环子群的全部生成元，所述生成元的数量为Kn，所述循环子群的全部生成元表示为其中u0＝0；

S4、根据所述步骤S3得到的全部生成元，构造(Kc+1)×(Kc+1)分块的基矩阵W，如公式(1)，每个子矩阵为(Kn+1)×(Kn+1)的矩阵，如公式(2)：

所述子矩阵Wi，j，0≤i≤Kc，0≤j≤Kc为：

所述基矩阵W的第i行分块第j列分块中的第s行第t列的元素等于所述循环子群中的第j个生成元除以第i个生成元乘上循环子群中的第t个生成元除以第s个生成元，然后减一，其中0≤i，j≤Kc、0≤s，t≤Kn，且循环子群和循环子群的第0个生成元均为1；

我们可以看出或证明所述基矩阵W拥有如下的特性：1)W每一行(列)中的所有元素都不相同；2)W中的任意两行在所有的(Kc+1)×(Kn+1)个位置均不相同；3)W中的每一行(列)有且仅有一个零元素；4)所有的零元素均在W的主对角线上，由上述的性质，我们可以证明W满足α幂次乘积的行距约束。

S5、根据步骤S4得到的基矩阵，将其的非零元扩展成(q-1)×(q-1)的循环置换矩阵，或广义循环置换矩阵，将所述基矩阵的零元扩展成(q-1)×(q-1)的零矩阵；得到如公式(3)形式的(Kc+1)(Kn+1)×(Kc+1)(Kn+1)的分块矩阵，即扩展矩阵H：

如果进行二元LDPC码的构造，则将所述基矩阵W中的非零元扩展成为二元的(q-1)×(q-1)循环置换矩阵，将所述基矩阵W中的零元扩展成为(q-1)×(q-1)零矩阵，得到一个二元的(q-1)×(q-1)分块校验矩阵H，其子矩阵为(q-1)×(q-1)的循环置换矩阵和零矩阵；所述非零元与扩展后的二元循环置换矩阵存在如下对应关系：W中的所有非零元均表示为本原元α的幂次方的形式，即α^e,0≤e＜q-1；与元素α^e对应的循环置换矩阵为e次循环右移后的q-1维标准阵；

如果进行多元LDPC码的构造，即二元以上LDPC码的构建，则将所述基矩阵W中的非零元扩展成为多元的(q-1)×(q-1)的广义循环置换矩阵，将W中的零元扩展成为(q-1)×(q-1)零矩阵，得到一个多元的(q-1)×(q-1)分块校验矩阵H，其子矩阵为(q-1)×(q-1)的广义循环置换矩阵和零矩阵；非零元与扩展后的广义循环置换矩阵存在如下对应关系：W中的所有非零元均表示为本原元α的幂次方的形式，即α^e,0≤e＜q-1；定义q-1维广义标准矩阵为主对角线上的元素为(α⁰，α¹，...，α^q-2)，其余元素均为0；与元素α^e对应的广义循环置换矩阵为q-1维广义标准矩阵e次循环右移后所有元素乘以αⁱ的q-1维广义标准阵，其中，α的幂取模q-1。

S6、选取所述扩展矩阵H的子矩阵H(γ，ρ)做校验矩阵，H(γ，ρ)的零空间给出所要构造的准循环LDPC码，具体为：

根据所述码长和码率的范围确定子矩阵的行分块数γ和列分块数ρ，其中所述列分块数ρ的取值使ρ(q-1)的值接近或等于要码长L；所述行分块数γ的取值使所要构造的校验矩阵的秩K接近或等于(1-R)ρ(q-1)的值；

从所述扩张矩阵H中选择连续的或者不连续的γ个行分块、ρ个列分块作为校验矩阵；若进一步要求校验矩阵中不含有全零子矩阵时，校验矩阵H(γ，ρ)选取要避开所述矩阵H中的零矩阵，即在主分块对角线上方或下方取值。

校验矩阵H(γ，ρ)的零空间给出了一个码长为ρ(q-1)、码率为1-K/ρ(q-1)，最小码距为γ的准循环LDPC码。若在H(γ，ρ)的选取中，要求避开H中的零子矩阵，则H(γ，ρ)的零空间给出一规则的循环LDPC码，若γ为奇数，则该码的最小码距为γ+1，若γ为偶数，则该码的最小码距为γ+2。

构造GF(q)上的二元LDPC码

1)参数设计：

选取q＝281做为码构造域。

2)有限域乘群中循环子群的确定：

q-1可以分解为281-1＝280＝8×35，取c＝8，n＝35。

3)基于循环子群的基矩阵的设计：

根据上述步骤S3的计算过程，计算两个循环子群的生成元，并根据所述生成元进行基矩阵的构造，我们得到一125×125的基矩阵，基矩阵中的每个元素均属于GF(2⁸)。

4)基矩阵的扩展：

对所取得基矩阵进行二元域上的扩展，得到125×125的分块校验矩阵，子矩阵为280×280的循环置换矩阵和零矩阵。

5)取扩展矩阵中的分块子矩阵作为校验矩阵：

此处取γ＝4，ρ＝16，避开主对角线上的零子矩阵，得到一4×16的分块子矩阵，子矩阵为280×280的循环置换矩阵，用此分块子矩阵作为校验矩阵。此矩阵的零空间给出一个(4480,3363)的准循环LDPC码，码率为0.751，其基于不同最大迭代次数(50次、10次、5次)的误比特性能曲线和对应的香农限如图2所示。

该码对应的基矩阵元素本原元的指数如下：

235 66 138 152 81 100 163 9 230 88 248 58 32 195 128 265

145 235 192 138 152 81 254 163 9 11888 95 240 32 195 128

52 145 221 192 138 152 236 254 163 230 118248 58 240 32 195

97 52 66 221 192 138 100 236 254 9 230 88 95 58 240 32

应用本发明的方法，有效简化了构造LDPC码的复杂度，并且该码保证了迭代译码中的良好收敛特性和低差错平底特性，够进行线性复杂度的编码，从而降低了信道编码对硬件的要求。

以上实施方式仅用于说明本发明，而非对本发明的限制。尽管参照实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，对本发明的技术方案进行各种组合、修改或者等同替换，都不脱离本发明技术方案的精神和范围，均应涵盖在本发明的权利要求范围当中。