一种基于楔石形变换的多分量实数线性调频信号变换技术的制作方法

本发明属于信号处理中时频分析领域，具体涉及一种基于楔石形变换的多分量实数线性调频信号变换技术。

背景技术：

在无线信号接收端处理时，为了估计和检测线性调频(LFM)信号，通常要求所使用技术具备高信号能量聚集性，同时要求交叉项足够低，防止干扰自项。而针对实数信号，还要求所用技术为实数域变换，防止虚数域干扰项出现。现有技术主要有傅里叶余弦变换类如离散余弦变换、时频余弦变换类如分数余弦变换。但由于它们均为线性变换，对LFM信号的能量聚集性均较差。双线性变换的信号自项能量聚集性优于线性变换，如维纳-威利分布(WVD)，可达到理论上最高聚集度。但WVD存在两个问题，一是会产生强交叉项，进而干扰信号自项的估计与检测；二是WVD为复数变换，不适用于实数信号。WVD的多种改进变换如平滑伪WVD等，因其受窗函数效应影响，均无法完美兼顾自项能量聚集性与交叉项问题。表1总结了现有技术的特点，由此可见当前缺乏同时满足三种要求的技术，即高信号自项能量聚集性、无交叉项、实数域变换。

表1现有技术针对多分量实数LFM信号处理特点

技术实现要素：

针对上述存在问题或不足，为同时满足高信号自项能量聚集性、无交叉项、实数域变换这三种要求，本发明提供了一种基于楔石形变换(keystone transform)的多分量实数线性调频LFM信号变换技术。

该基于楔石形变换的多分量实数LFM信号变换技术，具体技术方案包括如下步骤。

步骤1、对输入信号进行参数自相关计算；

输入信号为多分量实数LFM信号，表示为：

$s\left(t\right)=\underset{n=1}{\overset{N}{\Σ}}{A}_{n}cos(2{\mathrm{\πf}}_{n}t+{\mathrm{\π\γ}}_n{t}^2),---\left(1\right)$

其中N为该信号分量总数，A_n、f_n及γ_n分别表示第n个分量的幅值、中心频率及调频率；基于维纳-威利分布WVD思想，对式(1)进行参数自相关函数计算，其结果为：

$R_s=s(t+\frac{\mathrm{\τ}+1}{2})s(t-\frac{\mathrm{\τ}+1}{2})=U+Q+R_c=\frac{1}{2}\underset{n=1}{\overset{N}{\Σ}}{A}_n^{2}cos\left(2{\mathrm{\πf}}_n\right(\mathrm{\τ}+1)+2{\mathrm{\π\γ}}_n(\mathrm{\τ}+1\left)t\right)+Q+R_c,---\left(2\right)$

其中τ为延迟量，U为信号自相关项中的常项即自项常项，Q为自相关项中的高阶项，R_c为不同分量之间的交叉项。

步骤2、基于楔石形变换思想，将式(2)中U的相位中的时间量与延迟量解缠绕，对参数自相关函数R_s进行时间维伸缩变换：

设t_s为尺度时间即伸缩变换后的时间量，令t_s＝(τ+1)t，参数自相关函数R_s变为：

${\stackrel{\‾}{R}}_s=\frac{1}{2}\underset{n=1}{\overset{N}{\Σ}}{A}_n^{2}cos\left(2{\mathrm{\πf}}_n\right(\mathrm{\τ}+1)+2{\mathrm{\π\γ}}_n{t}_s)+\stackrel{\‾}{Q}+{\stackrel{\‾}{R}}_c,---\left(3\right)$

其中为尺度参数自相关函数；从式(3)第一项可见，相位中的时间量与延迟量已经解缠绕；

所述对参数自相关函数R_s进行时间维伸缩变换通过：针对时间维t的插值方法，离散傅里叶变换-傅里叶逆变换或尺度傅里叶变换-傅里叶逆变换来完成。

步骤3、进行两次傅里叶余弦变换，并求绝对值：

傅里叶余弦变换(FCT)定义为：

$S_{FCT}\left(f\right)={\∫}_0^{\mathrm{\∞}}s\left(t\right)cos\left(2\mathrm{\π}ft\right)dt.---\left(4\right)$

对尺度参数自相关函数即式(3)依次沿τ维、沿t_s维进行傅里叶余弦变换，并求绝对值，得最终结果：

$F_s(f,\mathrm{\γ})=|\frac{1}{8}cos\left(2\mathrm{\π}f\right)\underset{n=1}{\overset{N}{\Σ}}{A}_n^2\mathrm{\δ}(f-f_n)\mathrm{\δ}(\mathrm{\γ}-{\mathrm{\γ}}_n)+C_{t_s}\{C_{\mathrm{\τ}}\{\stackrel{\‾}{Q}+{\stackrel{\‾}{R}}_c\}\left\}\right|,---\left(5\right)$

其中C_τ{·}、分别表示沿τ维、沿t_s维傅里叶余弦变换；式(5)第一项表示信号各分量能量以δ函数形式聚集在频率-调频率平面的(f_n,γ_n)点上；第二项为自项高阶项及交叉项的运算结果。

对式(5)第二项进行计算，因在步骤2时间维伸缩过后，自项高阶项及交叉项的相位均不具备相干性，无法由傅里叶余弦变换进行相干累积，与第一项相比，第二项足够小；忽略第二项，式(5)进一步表示为：

$F_s(f,\mathrm{\γ})\≈\underset{n=1}{\overset{N}{\Σ}}{F}_{s_n}(f,\mathrm{\γ})\≈\frac{1}{8}\left|cos\left(2\mathrm{\π}f\right)\right|\underset{n=1}{\overset{N}{\Σ}}{A}_n^2\mathrm{\δ}(f-f_n)\mathrm{\δ}(\mathrm{\γ}-{\mathrm{\γ}}_n).---\left(6\right)$

本发明针对多分量实数LFM信号进行变换。运用楔石形变换的思想改进WVD变换，对信号自相关函数的时间量进行时间维伸缩变换，使其与延迟量二者解缠绕，从而达到信号自相关项可相干积累(提高自项能量聚集性)、交叉项无法相干积累(抑制交叉项)的目的。本发明对多分量实数LFM信号的变换结果为一个中心频率-调频率联合平面，信号自项能量在此平面上分布为尖峰。该尖峰幅值对应于时域幅值，该尖峰所在平面坐标对应于中心频率及调频率，由此获得信号的各分量参数值。基于式(6)可见本发明具有渐进线性。

本发明第一步基于WVD思想，属双线性变换。但最终结果近似为无交叉项，即同时具备线性变换的优点。因此在针对多分量实数LFM信号的处理上，兼具有双线性变换和线性变换的优点。由于本发明具备高信号自项能量聚集性与近似无交叉项的优点，可应用在强噪声中估计及检测信号，特别适用于负信噪比环境。

综上所述，本发明同时实现了信号自项能量聚集性高(近似达到WVD理论最高聚集度)、无明显交叉项(足够小可忽略，又称渐进线性)和实数域变换。

附图说明

图1为实施例具体技术方案流程图；

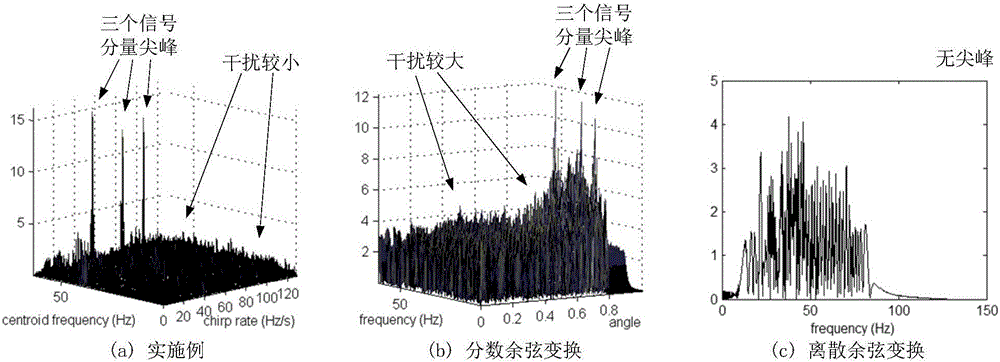
图2(a)、(b)、(c)分别为实施例、分数余弦变换和离散余弦变换对包含三个分量的实数LFM信号进行变换后的分布图；

图3(a)、(b)分别为实施例和分数余弦变换对受到高斯白噪声污染的信号进行变换后的分布图(SNR＝-2dB)。

具体实施方式

下面结合附图及具体实施方式对本发明作进一步的描述。

在计算机MATLAB环境下，根据式(1)产生仿真信号为：分量个数N＝3；幅值A_n均为1；中心频率为f₁＝47.5Hz、f₂＝27Hz、f₃＝26Hz；调频率为γ₁＝25Hz/s、γ₂＝14Hz/s、γ₃＝32Hz/s；采样频率f_s＝256Hz，信号采样点数N_s＝512。步骤2中对参数自相关函数R_s进行时间维伸缩变换通过：尺度傅里叶变换-傅里叶逆变换完成，如图1中第二个虚线框。

图2(a)、(b)、(c)分别表示本实施例、分数余弦变换、离散余弦变换对此信号进行变换后的分布。由此图可见：1)离散余弦变换无法对信号参数进行估计，因为该信号为LFM信号，离散余弦变换不适用于这种频率随时间变化的信号；2)分数余弦变换将信号三个分量均聚集为尖峰，并从尖峰坐标获得各自的频率及调频率，但尖峰点之外的干扰点较强；3)本发明同样将三个分量均聚集为尖峰，从尖峰坐标获得频率及调频率，且聚集性能高于分数余弦变换(尖峰点之外的干扰点均较弱)。因为本发明具有双线性变换的优点——聚集性高，而分数余弦变换是线性变换——聚集度中等。

图3(a)、(b)分别表示本实施例、分数余弦变换对受到高斯白噪声污染的信号进行变换后的分布，其输入信噪比SNR＝-2dB，SNR定义为10log₁₀(信号功率/噪声功率)，此时信号功率小于噪声功率。由图可见：1)在强噪声下(负信噪比，即噪声功率大于信号功率)，分数余弦变换无法检测到信号尖峰；2)本发明仍然能够检测到该信号的所有分量尖峰。

综上可见：通过仿真结果对比，对多分量实数LFM信号进行处理，本发明在信号能量聚集性方面优于分数余弦变换及离散余弦变换，且无明显交叉项。在强噪声下对信号进行检测时，本发明抗噪能力优于分数余弦变换。