螺旋型血管机器人姿轨一体化自适应滑模跟踪控制方法与流程

本发明属于控制技术领域。

背景技术：

近年来，在科技蓬勃发展的同时，不规律的生活习惯使越来越多的人们被心脑血管疾病所困扰。由于传统的手术治疗具有辐射伤害大、术后创口大且恢复缓慢的缺点，而微创手术独有的特点使其可以克服传统手术治疗的不足，从而成为了医学界关注的热点。将微创手术与机器人技术结合起来已经是医学界的主流发展趋势，有着广阔的发展前景。

血管机器人是针对心脑血管疾病问题尝试的一种新方法，血管机器人是指工作在血管环境中且可通过外部控制器实现工作要求的一种微型机器人。在生活中，不仅可以用血管机器人对癌变组织进行靶向治疗，在病患处精准投放药物；血管机器人还可以用来定时清除胆固醇和脂肪等血液沉积物，预防心脑血管疾病。同时血管机器人还具有相应的检测功能，可对人体的各个器官与组织进行诊断与检测。医生可以基于血管机器人的检测数据采取合理的治疗办法，最终大幅度地减少手术操作并减轻对患者的手术伤害。另外血管机器人还具有清除寄生虫和细菌，清洁伤口，粉碎结石等功能，既可以高效的解决患者的疾病问题，又能方便人们的生活。在血管机器人的辅助下可以大量减少传统手术带来的伤害，因而对血管机器人的研究逐渐演变为医学界的重要研究方向。

螺旋结构的血管机器人由磁性材料头部和螺旋型的尾部组成，由外部的三维旋转磁场提供动力。由于机器人螺旋运动产生的动压润滑效应可以有效地避免机器人与血管壁接触保护血管，经过综合考虑安全性和能源供给方式的稳定性与可实现性，外部旋转磁场驱动的具有螺旋结构的血管机器人具有较高的学术研究价值与广阔的医疗应用前景。因此本发明针对的对象即为螺旋型血管机器人。传统上，研究人员采用分别对血管机器人的运动轨迹和姿态进行建模，但血管机器人运动实际是会受到姿态轨迹耦合的影响。根据血管机器人的工作要求，必须保证血管机器人不会损伤人体血管壁。但在实际工作过程中，由于竖直方向重力-浮力的影响，血管机器人往往会发生相对于期望运动轨迹而下沉偏移的现象。而且传统控制方法对血管机器人的控制效果不佳。为了避免上述问题，在进行血管机器人的建模和控制时，应将上述实际情况考虑在内，因此，找到一种可以充分考虑血管机器人的姿轨耦合影响的建模解决方案，和可以考虑重力-浮力补偿的控制方案，对血管机器人在微创手术中的应用具有很大的意义。

技术实现要素：

本发明的目的是充分考虑血管机器人的姿轨耦合和重力-浮力的影响，且提高控制精度的螺旋型血管机器人姿轨一体化自适应滑模跟踪控制方法。

本发明步骤是：

步骤一：采用对偶四元数对螺旋型血管机器人的姿态和轨迹运动同时进行描述，建立螺旋型血管机器人的姿轨一体化运动学和动力学模型；

步骤二：针对螺旋型血管机器人在血液中运动时，会受到重力-浮力的影响，导致实际运动轨迹下沉偏移，而脱离期望轨迹，设计重力-浮力补偿器，对竖直方向重力-浮力的下沉作用进行补偿；

步骤三：基于步骤一建立的螺旋型血管机器人模型和步骤二设计的重力-浮力补偿器，设计基于重力-浮力补偿的滑模控制器；

步骤四：基于步骤三设计的滑模控制器，设计自适应滑模控制；

步骤一所述的姿轨一体化运动学和动力学模型建立的具体过程为：

单位对偶四元数描述的血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差为：

其中，和分别为利用单位对偶四元数表示的血管机器人期望坐标系odxdydzd和本体坐标系obxbybzb分别相对于惯性坐标系oxyz的姿轨，“*”表示对偶四元数的乘法，表示对偶四元数的共轭；

血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的速度旋量误差在坐标系obxbybzb下表示为：

其中，为血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的速度旋量在机器人本体坐标系obxbybzb中的表示，为血管机器人期望坐标系odxdydzd相对于惯性坐标系oxyz的速度旋量在期望坐标系odxdydzd中的表示，(·)^*表示对偶四元数的共轭；

进而通过推导可以得到基于的姿轨一体化运动学及动力学方程：

其中，m^b为对偶质量特性惯性矩阵，表示坐标系obxbybzb中作用点为血管机器人质心的对偶力旋量，“×”表示对偶四元数的叉乘运算，表示矩阵和对偶四元数的一种运算，对于对偶四元数定义的运算为ε表示对偶单位；定义的运算为为任一对偶四元数；

步骤二所述的重力-浮力补偿器具体设计过程为：

当血管机器人在血液中运动时，定义血管机器人的期望运动速度为在血液中的血管机器人主要受到总驱动力机器人的重力-浮力流体阻力的作用；

总驱动力的表达式为：

其中，表示在三维旋转磁场作用下血管机器人螺旋尾部旋转产生的驱动力，为磁梯度产生的磁拉力，n为血管机器人螺旋尾部的旋转圈数，d为血管机器人磁性球形头部直径，α1为血管机器人尾部螺旋升角，为血管机器人旋转角速度，v为血管机器人体积，m为磁化强度，为磁场梯度，ζ⊥为垂直于螺旋尾部的轴向阻力系数，且ζ11为平行于螺旋尾部的轴向阻力系数，且η为血液粘度系数，κ为血管机器人螺旋尾部直径；

流体阻力由血管机器人头部和螺旋尾部受血流冲击所产生的流体阻力组成，表示为：

机器人重力-浮力是重力g和浮力作用在竖直方向上的合力，其表达式为：

其中，ρ为血管机器人的密度，ρf为血液的密度，为重力加速度；

抵消重力-浮力对血管机器人的作用效果，需要流体阻力和总驱动力的共同作用，即：

其中为设计重力-浮力补偿器，建立血管机器人的姿态坐标系p，坐标系的原点op位于血管机器人重心，坐标系xp轴与血管机器人实际指向相重合，zp轴垂直于血管机器人实际指向为血管机器人为抵消重力-浮力影响的运动速度，

根据式(8)得：

将血管机器人期望运动速度分解为水平分量和竖直分量可知血管机器人期望运动速度的水平分量与的水平分量相等，即有血管机器人旋转角速度和三维旋转磁场的旋转角速度ω1有如下关系：

根据上述分析可得：

其中，为单位矢量；

当时，根据式(9)和(10)可得：

当时，将分解为两个力，即平行于xp轴的分量与垂直于xp轴的分量f⊥p在方向没有分量，又由于磁场梯度方向的不确定性和多变性，假设作用xpzp平面上且方向与血管机器人期望运动速度关于xp轴对称，则类似于的受力分析，可以分解为平行于xp轴的分量与垂直于xp轴的分量f⊥p_1在方向没有分量，则有：

其中，和分别表示在zp轴与xp轴投影的数量值，和在zp轴与xp轴投影的数量值，分别表示zp轴方向与xp轴方向的单位向量；将式(10)和(13)代入到式(9)，可得：

由于定义血管机器人期望俯仰角为将速度投影到xp轴，zp轴方向，并根据式(14)可得：

通过分析血管机器人姿态坐标系p的力学几何关系可得：

其中，β为血管机器人期望俯仰角向上倾斜的角度；

类似于式(16)中对于的分析，同样可得到以下关系：

根据式(15)，式(16)和式(17)，得到：

根据cos(θ+β)＝cos(θ)cos(β)-sin(θ)sin(β)，则由式(18)可得重力-浮力补偿器输出的血管机器人相比于理想俯仰角向上倾斜的角度β为：

通过式(15)，式(16)和式(17)可得，重力-浮力补偿器输出的三维旋转磁场的旋转角速度ω1为：

步骤三所述的基于重力-浮力补偿的滑模控制器为：

记血管机器人期望运动轨迹为[xd(t),yd(t),zd(t)]^t，设机器人初始滚转角速度则血管机器人期望偏航角ψ与期望俯仰角θ分别为：

假设血管机器人的滚转角速度与三维旋转磁场旋转角速度ω1一致，则在重力-浮力补偿器作用下血管机器人的偏航角ψ^s、俯仰角θ^s、滚转角速度为：

最后将上述血管机器人期望运动轨迹[xd(t),yd(t),zd(t)]^t与血管机器人经过重力-浮力补偿后的姿态角进行对偶四元数变换，得到对偶四元数框架下的运动描述从而将血管机器人期望坐标系的对偶四元数运动作为控制系统的输入；

血管机器人的控制目标为：通过控制血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差使血管机器人的实际运动状态渐进收敛到期望坐标系下的运动状态

基于步骤一中建立的血管机器人姿轨一体化运动学和动力学方程式(3)和式(4)，设计如下滑模面：

其中，为对偶数的积运算，为控制器参数，且ksi＞0，设计滑模控制律为：

其中，为滑模变量，sgn(·)为符号函数，且为控制器参数，且kεi＞0，为控制器参数，且kui＞0，为对偶矢量的一种积运算，为对偶干扰力；

步骤四所述的自适应滑模控制器为：

为便于设计自适应滑模控制器，将式(27)中带有m^b的项用下式表示：

其中，为对偶质量特性惯性矩阵m^b的另一种表达方式；且π∈r3×1，通过对偶极子运算的特殊性质ε²＝0可以进一步得到为三维对偶向量；由于对偶质量特性惯性矩阵m^b的特殊性可知π易得，而关于的计算，可由式(29)-(31)推导得出：对于任意x∈r3×1,y∈r3×1，有：

其中，δ(x,y)＝δ1(x)+δ2(y)，且δ1(x)，δ2(y)的计算方式如下：

由于血管机器人复杂的工作环境及多变的工作内容，在血管机器人建模过程中，其质量与惯量往往具有不确定性与多变性，因此为对偶质量特性惯性矩阵和对偶干扰力的估计值设计参数自适应律如下：

其中，为控制器参数，为控制器参数，且：

将式(32)和式(33)带入式(27)的滑模控制律，则可得到自适应滑模控制律为：

本发明针对血管机器人的建模和跟踪控制问题，建立了基于对偶四元数理论的血管机器人姿轨一体化动力学和运动学模型，解决了血管机器人在实际操作中姿态轨迹相互耦合从而影响血管机器人使用的问题。考虑到血管机器人在竖直方向受到重力-浮力的作用有下沉偏移运动的现象，设计重力-浮力补偿器来抵消下沉作用。基于建立的模型和构造的重力-浮力补偿器，设计带有重力-浮力补偿的自适应滑模控制。最后通过仿真分析，证明了设计的自适应滑模控制器相比于滑模控制器，不仅具有较好的快速性，而且可以更好的抑制滑模控制的抖动现象，提高姿态轨迹跟踪控制精度。对血管机器人在微创手术中得以应用具有很大的实际价值和理论意义。

附图说明

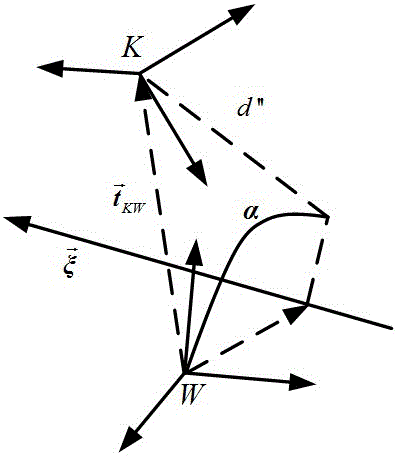
图1是对偶四元数表示的坐标系变换示意图；

图2是血管机器人由于重力-浮力影响进行下沉偏移及进行重力-浮力补偿后的示意图；

图3是血管机器人的物理结构及参数示意图；

图4是血管机器人重力-浮力补偿的受力分析图；

图5是血管机器人的滑模控制器框图；

图6是血管机器人跟踪直线型参考轨迹的运动轨迹跟踪曲线图；

图7是血管机器人跟踪直线型参考轨迹的运动轨迹误差曲线图；

图8是血管机器人跟踪直线型参考轨迹的偏航角跟踪曲线图；

图9是血管机器人跟踪直线型参考轨迹的偏航角跟踪误差图；

图10是血管机器人跟踪直线型参考轨迹的俯仰角跟踪曲线图；

图11是血管机器人跟踪直线型参考轨迹的俯仰角跟踪误差图；

图12是血管机器人跟踪直线型参考轨迹的滚转角速度跟踪曲线图；

图13是血管机器人跟踪直线型参考轨迹的滚转角速度跟踪误差图；

图14是血管机器人跟踪曲线型参考轨迹的运动轨迹跟踪曲线图；

图15是血管机器人跟踪曲线型参考轨迹的运动轨迹误差曲线图；

图16是血管机器人跟踪曲线型参考轨迹的偏航角跟踪曲线图；

图17是血管机器人跟踪曲线型参考轨迹的偏航角跟踪误差图；

图18是血管机器人跟踪曲线型参考轨迹的俯仰角跟踪曲线图；

图19是血管机器人跟踪曲线型参考轨迹的俯仰角跟踪误差图；

图20是血管机器人跟踪曲线型参考轨迹的滚转角速度跟踪曲线图；

图21是血管机器人跟踪曲线型参考轨迹的滚转角速度跟踪误差图。

具体实施方式

本发明本发明的步骤是：

步骤一：利用对偶四元数建立血管机器人的姿轨一体化动力学和运动学模型；

步骤二：由于血管机器人在实际运动中会受到重力-浮力影响而下沉偏移，设计重力-浮力补偿器来进行补偿；

步骤三：基于步骤一建立的血管机器人模型和步骤二设计的重力-浮力补偿器，设计基于重力-浮力补偿的滑模控制器；

步骤四：基于步骤三设计的滑模控制器，设计自适应滑模控制器。

步骤一的具体过程如下：

单位对偶四元数描述的血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差为：

其中，和分别为利用单位对偶四元数表示的血管机器人期望坐标系odxdydzd和本体坐标系obxbybzb分别相对于惯性坐标系oxyz的姿轨。“*”表示对偶四元数的乘法，表示对偶四元数的共轭。

血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的速度旋量误差在坐标系obxbybzb下表示为：

其中，为血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的速度旋量在机器人本体坐标系obxbybzb中的表示。为血管机器人期望坐标系odxdydzd相对于惯性坐标系oxyz的速度旋量在期望坐标系odxdydzd中的表示。(·)^*表示对偶四元数的共轭。

进而通过推导可以得到基于的姿轨一体化运动学及动力学方程：

其中，m^b为对偶质量特性惯性矩阵。表示坐标系obxbybzb中作用点为血管机器人质心的对偶力旋量。“×”表示对偶四元数的叉乘运算，表示矩阵和对偶四元数的一种运算。对于对偶四元数定义的运算为ε表示对偶单位；定义的运算为为任一对偶四元数。

步骤二的具体过程如下：

当血管机器人在血液中运动时，定义血管机器人的期望运动速度为在血液中的血管机器人主要受到总驱动力机器人的重力-浮力流体阻力的作用。在竖直方向重力和浮力的作用下，血管机器人往往相对于期望运动速度下沉偏移，因此设计重力-浮力补偿器，使血管机器人实现期望运动效果。此补偿器的输入为血管机器人的期望运动速度，输出为机器人相比于理想俯仰角向上倾斜的角度与三维旋转磁场的旋转角速度。

总驱动力的表达式为：

其中，表示在三维旋转磁场作用下血管机器人螺旋尾部旋转产生的驱动力，为磁梯度产生的磁拉力。n为血管机器人螺旋尾部的旋转圈数，d为血管机器人磁性球形头部直径，α1为血管机器人尾部螺旋升角，为血管机器人旋转角速度，v为血管机器人体积，m为磁化强度，为磁场梯度。ζ⊥为垂直于螺旋尾部的轴向阻力系数，且ζ11为平行于螺旋尾部的轴向阻力系数，且η为血液粘度系数，κ为血管机器人螺旋尾部直径。

流体阻力由血管机器人头部和螺旋尾部受血流冲击所产生的流体阻力组成，可表示为：

机器人重力-浮力是重力g和浮力作用在竖直方向上的合力，其表达式为：

其中，ρ为血管机器人的密度，ρf为血液的密度，为重力加速度。

通过对血管机器人的受力分析可知，如果要抵消重力-浮力对血管机器人的作用效果(下沉)，需要流体阻力和总驱动力的共同作用，即：

其中，

为设计重力-浮力补偿器，建立血管机器人的姿态坐标系p。坐标系的原点op位于血管机器人重心，坐标系xp轴与血管机器人实际指向相重合，zp轴垂直于血管机器人实际指向为血管机器人为抵消重力-浮力影响的运动速度。

根据式(8)可得：

将血管机器人期望运动速度分解为水平分量和竖直分量可知血管机器人期望运动速度的水平分量与的水平分量相等，即有

血管机器人旋转角速度和三维旋转磁场的旋转角速度ω1有如下关系：

根据上述分析可得：

其中，为单位矢量。

当时，根据式(9)和(10)可得：

当时，将分解为两个力，即平行于xp轴的分量与垂直于xp轴的分量(f⊥p在方向没有分量)。又由于磁场梯度方向的不确定性和多变性，假设作用xpzp平面上且方向与血管机器人期望运动速度关于xp轴对称。则类似于的受力分析，可以分解为平行于xp轴的分量与垂直于xp轴的分量(f⊥p_1在方向没有分量)，则有：

其中，和分别表示在zp轴与xp轴投影的数量值，和在zp轴与xp轴投影的数量值。分别表示zp轴方向与xp轴方向的单位向量。

将式(10)和(13)代入到式(9)，可得：

由于定义血管机器人期望俯仰角为将速度投影到xp轴，zp轴方向，并根据式(14)可得：

通过分析血管机器人姿态坐标系p的力学几何关系可得：

其中，β为血管机器人期望俯仰角向上倾斜的角度。

类似于式(16)中对于的分析，同样可得到以下关系：

根据式(15)，式(16)和式(17)，可以得到：

根据cos(θ+β)＝cos(θ)cos(β)-sin(θ)sin(β)，则由式(18)可得重力-浮力补偿器输出的血管机器人相比于理想俯仰角向上倾斜的角度β为：

通过式(15)，式(16)和式(17)可得，重力-浮力补偿器输出的三维旋转磁场的旋转角速度ω1为：

步骤三的具体过程如下：

记血管机器人期望运动轨迹为[xd(t),yd(t),zd(t)]^t，设机器人初始滚转角速度则血管机器人期望偏航角ψ与期望俯仰角θ分别为：

假设血管机器人的滚转角速度与三维旋转磁场旋转角速度ω1一致，则在重力-浮力补偿器作用下血管机器人的偏航角ψ^s、俯仰角θ^s、滚转角速度为：

最后将上述血管机器人期望运动轨迹[xd(t),yd(t),zd(t)]^t与血管机器人经过重力-浮力补偿后的姿态角进行对偶四元数变换，得到对偶四元数框架下的运动描述从而将血管机器人期望坐标系的对偶四元数运动作为控制系统的输入。

血管机器人的的控制目标为：通过控制血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差使血管机器人的实际运动状态渐进收敛到期望坐标系下的运动状态

基于步骤1中建立的血管机器人姿轨一体化运动学和动力学方程式(3)和式(4)，设计如下滑模面：

其中，为对偶数的积运算。为控制器参数，且ksi＞0，

设计滑模控制律为：

其中，为滑模变量，sgn(·)为符号函数，且为控制器参数，且kεi＞0，为控制器参数，且kui＞0，为对偶矢量的一种积运算。为对偶干扰力。

步骤四的具体过程如下：

步骤三设计的滑模控制器存在抖动现象，并且血管机器人在临床医疗应用过程中，常常需要面临具有差别性的工作任务与工作环境，所以血管机器人的模型参数具有无法估计的变化特性及不确定性，(主要体现在血管机器人中对偶质量特性惯性矩阵m^b的不准确性及对偶干扰力的不确定性)，因此为了解决模型参数不确定与不准确问题并抑制滑模控制器中的抖动问题，设计自适应滑模控制器以提高血管机器人系统的控制性能及控制精度。

为便于设计自适应滑模控制器，将式(27)中带有m^b的项用下式表示：

其中，为对偶质量特性惯性矩阵m^b的另一种表达方式；且π∈r3×1，通过对偶极子运算的特殊性质ε²＝0可以进一步得到为三维对偶向量；由于对偶质量特性惯性矩阵m^b的特殊性可知π易得，而关于的计算，可由式(29)-(31)推导得出：对于任意x∈r3×1,y∈r3×1，有：

其中，δ(x,y)＝δ1(x)+δ2(y)，且δ1(x)，δ2(y)的计算方式如下：

由于血管机器人复杂的工作环境及多变的工作内容，在血管机器人建模过程中，其质量与惯量往往具有不确定性与多变性，因此为对偶质量特性惯性矩阵和对偶干扰力的估计值设计参数自适应律如下：

其中，为控制器参数，为控制器参数，且：

将式(32)和式(33)带入式(27)的滑模控制律，则可得到自适应滑模控制律为：

下面结合附图对本发明做进一步的详细说明

首先对四元数和对偶四元数做出基本的说明

四元数

四元数是hamilton在1843年提出的一种数学理论，它的形式为：

其中，l0为实数，表示四元数的标量部分；表示四元数的矢量部分；lv1、lv2、lv3为实数，均为正交向量，且

四元数的基本运算法则有：

其中，l1、l2表示四元数；λ为一实数；l^*表示四元数l的共轭；||l||表示四元数l的模，且定义模为1的四元数为单位四元数；l^-1表示四元数l的逆；vec(l)表示对四元数l进行向量转换的运算，即l的第一个元素取为0，使l成为向量。

为方便计算，将矩阵和四元数的运算定义为：

其中，为四阶矩阵。

“*”表示四元数的乘法，具体计算为：

其中，e3表示三阶单位阵，且为叉乘矩阵。

通过推导可得：

特别地，在及条件下，分别定义如下计算：

定义四元数的“×”运算为：

对偶数

对偶数由数学家clifford提出，并将其定义为：

其中，a，为实数且分别为实数部分与对偶部分；ε表示对偶单位，ε²＝0且ε≠0。

对偶数有如下运算：

其中，均为对偶数；μ为一实数。

为了方便计算，定义对偶数的运算为：

对偶矢量

当对偶数的实数部分与对偶部分均为三维矢量时，此对偶数定义为对偶矢量，即其中当对偶矢量中的实数部分是自由矢量而对偶部分是定位矢量时(即实数部分的矢量与选取的参考点无关，而对偶部分的矢量与选取的参考点有关)，此对偶矢量叫做旋量。对偶矢量的基本运算如下：

定义关于对偶矢量取绝对值的运算“<>”：

由式(1012)的表达可知：“<>”代表各项元素均为正的对偶矢量。

定义为对偶矢量的一种积运算，其具体计算为：

进而通过计算可以得到：

由式(1014)可知，经过运算所得到的结果为一个新的对偶矢量。

定义对偶向量的内积运算，符号为“||·||”，具体计算见下式：

由上式可知，对偶矢量的内积运算结果为一实数。

对偶动量

定义当刚体质心ec为对偶动量的参考点时，刚体的对偶动量可表示为：

其中，m为刚体质量，为刚体速度，表示以质心ec为参考点的刚体线动量，λe表示在本体坐标系下的质心ec的转动惯量矩阵，为刚体角速度，表示将质心ec视为参考点的刚体角动量。

对式(1016)进行求导，则得参考点ec在质心时的newton-euler刚体动力学方程：

其中，为对偶力旋量，与分别为质心作用点上的外力和力矩。

对偶四元数

对偶四元数是各元素皆为对偶数的四元数或由四元数作为实数部分与对偶部分的对偶数，定义为：

其中，l和代表任一四元数；表示对偶数，表示对偶向量；

根据对偶四元数的定义可知，对偶四元数和四元数的基本运算法则是类似的，此处不再赘述。

为便于后面分析理解，此处将矩阵和对偶四元数运算定义为如下形式：

其中，为八阶矩阵。

为便于后面分析理解，类似于四元数中式(1006)和(1007)定义的运算，对偶四元数中也类似的定义了和的运算。

利用对偶四元数建立血管机器人的姿轨一体化动力学和运动学模型：

定义血管机器人本体坐标系为obxbybzb，惯性坐标系为oxyz，期望坐标系为odxdydzd。

基于单位四元数的血管机器人姿态运动学方程：首先用单位四元数描述血管机器人的三维旋转运动。

由euler定理可得，当一个刚体绕定点作旋转运动时可理解为该刚体绕通过定点的某一直线轴旋转一定角度，进而可得用四元数表示坐标系n绕轴旋转α角得坐标系m的运动描述：

其中，故lmn为单位四元数。且

由于惯性坐标系oxyz为血管机器人运动过程中的参考定坐标系，则利用单位四元数表示的血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的姿态运动学方程为：

其中，分别为血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的角速度在机器人本体坐标系obxbybzb和惯性坐标系oxyz中的表示。

同理可得用单位四元数表示期望坐标系odxdydzd相对于惯性坐标系oxyz的姿态运动学方程为：

其中，分别为血管机器人期望坐标系odxdydzd相对于惯性坐标系oxyz的角速度在期望坐标系odxdydzd和惯性坐标系oxyz中的表示。

由于单位四元数具有乘性误差性质，则血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿态误差le为：

血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的角速度即角速度误差在坐标系obxbybzb下表示为：

其中，

对式(1)进行微分运算并代入式(1021)、(1022)和式(1024)可得，血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿态误差运动学方程为：

其中，为血管机器人本体坐标系obxbybzb相对于期望作标系odxdydzd的误差角速度在坐标系odxdydzd下的表示。

基于对偶四元数的血管机器人姿轨一体化运动学方程：上述的单位四元数只描述了血管机器人的三维旋转运动(即姿态运动)，而对偶四元数可以将旋转和平移运动在同一个数学表达式中进行表示，因此采用对偶四元数描述血管机器人的三维旋转和平移运动(即姿轨一体化运动)。

由chasles定理可知，螺旋运动可以用来描述刚体的一般性运动，而刚体本体坐标系的空间六自由度转动运动以及平移运动可以使用对偶四元数同时进行描述。图1是描述w坐标系先绕旋转轴旋转α角再沿线的方向平移d”距离到k坐标系的过程。此过程用单位对偶四元数表示为：

其中，

设空间中有一直线，在w坐标系与k坐标系中分别表示为与根据式(6)可得进一步得到：

其中，为k坐标系相对于w坐标系的位置在k坐标系中的表示。则k坐标系相对于w坐标系的运动可描述为：

其中，为k坐标系相对于w坐标系的位置在w坐标系中的表示。

结合式(1025)，并对式(1028)进行求导，可以得到利用对偶四元数理论描述的姿轨一体化运动学方程：

其中，为k坐标系相对于w坐标系的速度旋量在k坐标系中的表示，为k坐标系相对于w坐标系的速度旋量在w坐标系中的表示。

结合式(1021)和式(1029)可得，基于单位对偶四元数的血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的运动学方程即惯性坐标系下血管机器人的姿轨一体化运动学方程为：

其中，分别为血管机器人本体坐标系obxbybzb相对于惯性坐标系oxyz的速度旋量在机器人本体坐标系obxbybzb和惯性坐标系oxyz中的表示。

同样结合式(1022)和式(1029)可得，对偶四元数理论中描述血管机器人惯性坐标系oxyz相对于期望坐标系odxdydzd的姿轨一体化运动学方程为：

其中，分别为血管机器人期望坐标系odxdydzd相对于惯性坐标系oxyz的速度旋量在期望坐标系odxdydzd和惯性坐标系oxyz中的表示。

单位对偶四元数具有和单位四元数类似的乘性误差性质，则血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差为：

根据式(1025)和式(1029)可得对偶四元数框架下的血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨一体化运动学方程为：

其中，和为血管机器人本体坐标系obxbybzb相对于期望作标系odxdydzd的速度旋量误差在坐标系obxbybzb和坐标系odxdydzd下的表示。

基于对偶四元数的血管机器人姿轨一体化动力学方程：

为了便于分析，假设血管机器人为刚体，根据式(1017)，可得以质心为参考点的血管机器人动力学方程：

其中，表示坐标系obxbybzb中作用点为血管机器人质心的对偶力旋量，表示在坐标系obxbybzb下的作用点在血管机器人质心上的合力，其中表示总驱动力，表示机器人的重力-浮力，表示流体阻力，表示对偶干扰力。

表示在坐标系obxbybzb中作用在血管机器人质心上的合力矩，其中分别表示驱动力矩，机器人的重力-浮力矩，流体阻力矩和对偶干扰力矩。为以血管机器人质心为参考点的对偶动量。

定义对偶质量特性惯性矩阵为：

其中，λb为本体坐标系obxbybzb下的血管机器人转动惯量矩阵，m为血管机器人质量。

定义并结合式(1016)与式(1019)，则有：

根据式(1036)对式(1034)进行推导，可得：

基于式(1024)中用四元数表示的角速度误差，可得用对偶四元数表示的坐标系obxbybzb下的血管机器人本体坐标系obxbybzb相对于血管机器人期望坐标系odxdydzd的速度旋量误差为：

对式(1038)求导，进而由式(1027)、式(1033)可推导出：

将式(1037)代入式(1039)中，经过进一步推导可得基于对偶四元数理论的血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨一体化动力学方程为：

综上，基于对偶四元数建立的血管机器人姿轨一体化运动学和动力学方程为：

设计血管机器人的重力-浮力补偿器：

当血管机器人在血液中运动时，为满足血管机器人可以在血管中往复运动的工作要求，假设血管机器人逆血液流速运动，即血管机器人的期望运动速度与血液流速方向相反，为血管机器人实际运动速度。在血液中的血管机器人主要受到以下几个力的作用：总驱动力机器人的重力-浮力流体阻力(由于血管机器人受到的静电力与范德华力非常小，此处忽略不计)。在竖直方向的重力-浮力作用下，血管机器人往往会出现相对于期望运动速度下沉偏移的现象，因此设计重力-浮力补偿器，输入为血管机器人的期望运动速度，输出为机器人相比于理想俯仰角向上倾斜的角度与三维旋转磁场的旋转角速度。即在传统控制策略的基础上，使血管机器人配合磁场旋转角速度在不同期望运动轨迹要求下相对于传统期望姿态向上倾斜补偿一定角度，使血管机器人实现期望运动效果。机器人下沉偏移及进行重力-浮力补偿后的示意图如图2所示。

总驱动力的表达式为：

其中，表示在三维旋转磁场作用下血管机器人螺旋尾部旋转产生的驱动力，为磁梯度产生的磁拉力。n为血管机器人螺旋尾部的旋转圈数，d为血管机器人磁性球形头部直径，α1为血管机器人尾部螺旋升角，ζ⊥为垂直于螺旋尾部的轴向阻力系数，ζ11为平行于螺旋尾部的轴向阻力系数。为血管机器人旋转角速度，v为血管机器人体积，m为磁化强度，为磁场梯度。

总驱动力的计算需要求取ζ⊥和ζ11这两个参数的值，二者分别为：

其中，η为血液粘度系数，κ为血管机器人螺旋尾部直径。血管机器人物理结构及参数示意图如图3所示。

流体阻力由血管机器人头部和螺旋尾部受血流冲击所产生的流体阻力组成，可表示为：

机器人重力-浮力是重力g和浮力作用在竖直方向上的合力，其表达式为：

其中，ρ为血管机器人的密度，ρf为血液的密度，为重力加速度。

通过图2对血管机器人的受力分析可知，如果要抵消重力-浮力对血管机器人的作用效果(下沉)，需要流体阻力和总驱动力的共同作用，即：

其中，

为设计重力-浮力补偿器，建立血管机器人的姿态坐标系p，如图4所示。坐标系的原点op位于血管机器人重心，坐标系xp轴与血管机器人实际指向相重合，zp轴垂直于血管机器人实际指向为血管机器人期望运动速度，为血管机器人为抵消重力-浮力影响的运动速度。

根据式(1048)可得：

由图4可知，将血管机器人期望运动速度分解为水平分量和竖直分量易知血管机器人期望运动速度的水平分量与的水平分量相等，即有

血管机器人旋转角速度和三维旋转磁场的旋转角速度ω1有如下关系：

则由图4可得：

其中，为单位矢量。

当时，根据图4和式(49)，式(50)可得：

当时，将分解为两个力，即平行于xp轴的分量与垂直于xp轴的分量易知f⊥p在方向没有分量，则有：

其中，分别表示在zp轴与xp轴投影的数量值；分别表示zp轴方向与xp轴方向的单位向量。

由于磁场梯度方向的不确定性和多变性，假设作用xpzp平面上且方向与血管机器人期望运动速度关于xp轴对称，则类似于的受力分析，可以分解为平行于轴xp轴的分量与垂直于xp轴的分量易知f⊥p_1在方向没有分量，则有：

其中，分别表示在zp轴与xp轴投影的数量值。

将式(1050)，式(1053)和式(1054)带入到式(1049)，可得：

由于定义图4中血管机器人期望俯仰角为将速度投影到xp轴，zp轴方向，并根据式(55)得到：

通过分析图4的力学几何关系可得：

其中，β为血管机器人期望俯仰角向上倾斜角度。

类似于图4和式(1057)中对于的分析，同样可得到以下关系：

根据式(1056)，式(1057)，式(1058)，可得：

由于cos(θ+β)＝cos(θ)cos(β)-sin(θ)sin(β)，则由式(1059)可得重力-浮力补偿器输出的血管机器人相比于理想俯仰角向上倾斜的角度β为：

通过式(1056)，式(1057)，式(1058)可得：重力-浮力补偿器输出的三维旋转磁场的旋转角速度ω1为：

设计血管机器人的基于重力-浮力补偿的滑模控制器：

血管机器人的滑模控制框图如图5所示。

记血管机器人期望运动轨迹为[xd(t),yd(t),zd(t)]^t，设机器人初始滚转角速度则血管机器人期望偏航角ψ与期望俯仰角θ分别为：

假设血管机器人的滚转角速度与三维旋转磁场旋转角速度ω1一致，则在重力-浮力补偿器作用下血管机器人的偏航角ψ^s、俯仰角θ^s、滚转角速度为：

最后将上述血管机器人期望运动轨迹[xd(t),yd(t),zd(t)]^t与血管机器人经过重力-浮力补偿后的姿态角进行对偶四元数变换，得到对偶四元数框架下的运动描述从而将血管机器人期望坐标系的对偶四元数运动作为控制系统的输入。

血管机器人的的控制目标为：通过控制血管机器人本体坐标系obxbybzb相对于期望坐标系odxdydzd的姿轨误差使血管机器人的实际运动状态渐进收敛到期望坐标系下的运动状态

基于步骤1中建立的血管机器人姿轨一体化运动学和动力学方程式(1041)和式(1042)，设计如下滑模面：

其中，的运算见式(1011)。为控制器参数，且ksi＞0，

设计滑模控制律为：

其中，为滑模变量，sgn(·)为符号函数，且为控制器参数，且kεi＞0，为控制器参数，且kui＞0，且关于的运算见式(1013)。

滑模控制器稳定性证明

对于血管机器人这个非线性系统，滑模控制器的稳定性证明主要有两步：首先证明控制系统在任何初始状态下都能收敛至再进一步证明闭环控制系统在滑模面上的稳定性。

以下是具体证明过程：

第一步：证明控制系统在任何初始状态下都能收敛至设计如下lyapunov函数：

其中，“||·||”的计算见式(1015)。

由于m^b为正定对称阵，则有v1≥0，并且当且仅当时有v1＝0；对上式求导并将式(67)带入，可得：

其中，

将血管机器人姿轨一体化动力学方程式(1042)代入式(1070)，可得：

将式(1068)代入式(1071)可以得到：

其中，<·>的具体计算见式(1012)。

第二步：证明闭环控制系统在滑模面上的稳定性。

定义如下lyapunov函数：

易知v2≥0，仅当时有v2＝0；对式(1073)求导：

进而经过计算有：

经过对式(1075)中的这一项进行推导,可得：

将(1076)继续推导可得：

同理，对式(1075)中的另外两项，推导过程类似式(1076)和式(1077)，此处不再赘述。

根据对式(1076)、式(1077)推导过程的分析，可以将式(1075)写成：

当时，可得代入式(1078)，可得：

故而得证。

步骤4：设计血管机器人的自适应滑模控制器：

步骤3设计的滑模控制器存在抖动现象，并且血管机器人在临床医疗应用过程中，常常需要面临具有差别性的工作任务与工作环境，所以血管机器人的模型参数具有无法估计的变化特性及不确定性，(主要体现在血管机器人中对偶质量特性惯性矩阵m^b的不准确性及对偶干扰力的不确定性)，因此为了解决模型参数不确定与不准确问题并抑制滑模控制器中的抖动问题，设计自适应滑模控制器以提高血管机器人系统的控制性能及控制精度。

为便于设计自适应滑模控制器，将式(68)中带有m^b的项用下式表示：

其中，为对偶质量特性惯性矩阵m^b的另一种表达方式；且π∈r3×1，通过对偶极子运算的特殊性质ε²＝0可以进一步得到为三维对偶向量；由于对偶质量特性惯性矩阵m^b的特殊性可知π易得，而关于的计算，可由式(1081)-(1083)推导得出：对于任意x∈r3×1,y∈r3×1，有：

其中，δ(x,y)＝δ1(x)+δ2(y)，且δ1(x)，δ2(y)的计算方式如下：

由于血管机器人复杂的工作环境及多变的工作内容，在血管机器人建模过程中，其质量与惯量往往具有不确定性与多变性，因此为对偶质量特性惯性矩阵和对偶干扰力的估计值设计参数自适应律如下：

其中，为控制器参数，为控制器参数，且：

将式(1084)和(1085)带入式(1068)的滑模控制律，则可得到自适应滑模控制律为：

自适应滑模控制器稳定性证明

由于步骤3已证明血管机器人的滑模控制器在上的稳定性，因此本步骤中只需证明控制系统能在自适应律的作用下收敛于滑模面。定义如下lyapunov函数：

其中，且有为估计误差，并定义故对任意有va≥0，并且当且仅当时有va＝0。

对上述lyapunov函数求关于时间t的导数，有：

根据步骤3中的式(70)，式(71)可知：

将血管机器人姿轨一体化动力学方程式(1042)入式(1090)可得：

进而将自适应滑模控制律式(1087)代入式(1091)，可得：

将上式带入式(1089)中，可得：

管机器人的各个质量系数及所受扰动变化比较缓慢，则有：进而可以得到：

对式(1093)中的这一项进行推导可得：

结合式(1086)，式(1087)与式(1096)，代入式1093)可得：

故而得证。

采用下列具体实施例来验证本发明的有益效果。

实施例一：用步骤4设计的自适应滑模控制器对血管机器人的直线型运动轨迹进行跟踪，并与步骤3设计的滑模控制器做对比，来验证自适应滑模控制器的控制效果。

血管机器人仿真参数设置：

表1血管机器人仿真参数

选取血管机器人起点为坐标原点，设计如下直线型参考轨迹曲线：

利用重力-浮力补偿器进行姿态补偿，并通过自适应滑模控制方法进行仿真，控制器参数为：

通过仿真，得到血管机器人在滑模控制器和自适应滑模控制器作用下跟踪直线型运动轨迹的仿真结果，如图6-13所示。由图6，图7可知在滑模控制与自适应滑模控制作用下，血管机器人轨迹控制都有较好的跟踪精度，而且自适应滑模控制显然要优于滑模控制，主要表现为自适应滑模控制可以满足更高的控制精度要求；并且相较于滑模控制，自适应滑模控制在血管机器人轨迹控制中节约了大部分的误差收敛调节时间，有较高的系统响应快速性。图8-13是血管机器人的姿态控制结果，从图中可知，相比于滑模控制，自适应滑模控制具有更高的姿态跟踪控制精度，并且调节时间短。另外，由姿态角的误差图9、图11、图13可知，自适应滑模控制相较于滑模控制具有更好的抗抖动性能，有助于提高控制系统稳定性。

实施例二：用步骤4设计的自适应滑模控制器对血管机器人的曲线型运动轨迹进行跟踪，并与步骤3设计的滑模控制器做对比，来验证自适应滑模控制器的控制效果。

机器人仿真参数的设置同实施例一。

为了验证自适应滑模控制器针对不同工况下的有效性，应对多变的工作条件，本实施例中对曲线型运动轨迹进行跟踪。

令血管机器人起点为坐标原点，设计血管机器人运动轨迹曲线：

利用重力-浮力补偿器进行姿态补偿，并通过自适应滑模控制方法进行仿真，控制器参数设置为：

通过仿真，得到血管机器人在滑模控制器和自适应滑模控制器作用下跟踪曲线型运动轨迹的仿真结果，如图14-21所示。图14-15是血管机器人在滑模控制器和自适应滑模控制器作用下的运动轨迹结果图。由图可知，与滑模控制相比，自适应滑模控制在血管机器人轨迹控制中节约了大部分的误差收敛调节时间，并且系统响应速度较快。图16-21是血管机器人的姿态控制结果，从图中可知，自适应滑模控制的姿态跟踪误差比滑模控制的姿态跟踪误差要小很多，并且调节时间短。验证了提出的自适应滑模控制方法具有更高的姿态跟踪控制精度。另外，由姿态角的误差图17、图19和图21可知，自适应滑模控制相较于滑模控制具有更好的抗抖动性能，提高了控制系统稳定性。