一种柔性关节机械臂控制方法与流程

本发明涉及一种柔性关节机械臂控制方法。

背景技术：

近三十年来，柔性关节机械臂以其小巧的执行机构、高精度、低能耗的特点引起了人们的广泛关注。与刚性机械臂相比，柔性关节机械臂具有灵活性强、安全性高、损伤率低等优点。柔性关节机械臂由于其固有的高度耦合、非线性和模型不确定性，在建模和控制中存在着严重的问题。因此，这提高了控制器设计的难度，使得大量的研究使用先进的控制理论来设计更合适的控制器。

目前，已有一些对于柔性关节机械臂的控制方法。自适应控制已广泛应用于柔性关节机械臂的控制器设计，研究成果比较成熟。针对机械臂系统的不匹配问题，自适应反演控制器不需要由控制律推导的不确定参数的界限。然而，许多现有的控制技术在一些温和的假设下才被应用到柔性关节机械臂上。事实上，机器人的运动是一个复杂的非线性过程，很难将其建模看成线性参数过程。函数逼近技术在解决这一问题上具有很大的优势，它不需要精确地知道系统动力学。神经网络、自递归小波神经网络和模糊系统确实在逼近各种非线性函数时具有较明显的优势。二型模糊系统能够有效地提高系统处理不确定性和逼近不确定未知函数的能力。然而，在柔性关节机械手的跟踪控制上，利用二型模糊逼近器设计自适应控制器的研究较少。

技术实现要素：

本发明的目的是提供一种柔性关节机械臂控制方法，能够满足柔性关节机械臂对鲁棒控制技术的高精度要求，显著提高了柔性关节机械手的控制稳定性。

一种柔性关节机械臂控制方法，其特别之处在于，包括如下步骤：

步骤一：建立柔性关节机械臂系统动力学模型；

步骤二：将柔性关节机械臂期望的关节和电机的位移、角速度作为基于模糊神经网络逼近器的自适应反演控制器的参考输入，将电动机提供转矩的外部输入作为自适应反演控制器的实际输入，如果自适应反演控制器的实际输出值和预设的期望值产生跟踪误差，该跟踪误差通过自适应反演控制器的迭代计算趋近于零。

步骤一中动力学模型如下：

其中q1∈rⁿ和q2∈rⁿ分别是柔性关节连杆角位移和电机位移，和分别是柔性关节连杆角加速度和电机加速度，g是重力加速度，k是关节的弹簧刚度，u∈rⁿ是由电动机提供转矩的外部输入，i和j分别是柔性关节连杆与电机的转动惯量，m是柔性关节连杆的重量，l是机械臂重心与柔性关节之间的长度。

步骤二中迭代计算具体如下：

步骤1：定义e1＝x1-x1d并且令x1d＝yd；

其中e1是误差，x1＝q1即柔性关节连杆角位移，x1d是虚拟控制器，yd是期望值；

定义e2＝x2-x2d以及虚拟控制器

其中e2是误差，即柔性关节连杆角速度，x2d是虚拟控制器，是x1d的时间导数，其中k1是一个非负的常数；

步骤2：定义e3＝x3-x3d以及虚拟控制器

其中e3是误差，x3＝q2即电机位移，x3d是虚拟控制器，是x2d的时间导数，k2是一个非负常数，是g的估计值，g是未知非线性函数；

此时运用区间二型模糊神经网络逼近器，得到g的逼近值

其中是αg的估计值，αg是自适应因子，是的估计值，是二型模糊集的上后件值，是θg的估计值，θg是二型模糊集的下后件值，ξg是下基函数的向量，是上基函数的向量；

其中ξ(x)和的计算如下：

其中和分别是上下隶属函数，具体选择为高斯函数；i＝1,2,3,4为状态数，k为模糊规则数；

其中和而和的更新自适应律如下：

其中是的迭代更新值，是的迭代更新值，γg、λg、和是常数；

步骤3：定义e4＝x4-x4d以及虚拟控制器

其中e4是误差，即电机速度，x4d是虚拟控制器，是不含模型信息的已知部分，k3是一个非负常数，是d的估计值，d是未知非线性函数；

此时运用区间二型模糊神经网络逼近器，得到d的逼近值

其中是αd的估计值，αd是自适应因子，是的估计值，是二型模糊集的上后件值，是θd的估计值，θd是二型模糊集的下后件值，ξd是下基函数的向量，是上基函数的向量；

其中ξ(x)和的计算如下：

其中和分别是上下隶属函数，具体选择为高斯函数。i＝1,2,3,4为状态数和k为模糊规则数；

其中和而和的更新自适应律如下：

其中是的迭代更新值，是的迭代更新值，γd、λd、和是常数；

步骤4：选择如下控制律：

其中是h的估计值、是m的估计值以及k4是非负常数；

其中是不含模型信息的已知部分，k4是一个非负常数，是h的估计值，h是未知非线性函数，是m的估计值，m是未知非线性函数；

将的自适应律选为非线性函数可表示为：

其中满足如下不等式是初始值，m是常数。是的迭代更新值，γm是常数；

此时运用区间二型模糊神经网络逼近器，得到h的逼近值

其中是αh的估计值，αh是自适应因子，是的估计值，是二型模糊集的上后件值，是θh的估计值，θh是二型模糊集的下后件值，ξh是下基函数的向量，是上基函数的向量；

其中ξ(x)和的计算如下：

其中和分别是上下隶属函数，具体选择为高斯函数；i＝1,2,3,4为状态数和k为模糊规则数；

其中和而和的更新自适应律如下：

其中是的迭代更新值，是的迭代更新值，γh、λh、和是常数；

步骤5：将控制律u作为柔性关节机械臂系统的控制输入，产生实际的关节位移，即y＝x1；

步骤6：实际的关节位移y和期望值yd产生跟踪误差e1；

步骤7：回到步骤1，通过迭代计算直至e1、e2、e3、e4小于0.001。

本发明方法提出了一种基于it2fnn逼近器的柔性关节机械臂自适应反演控制方法，该方法利用李雅普诺夫稳定性理论，保证闭环系统中的所有信号最终都是有界的，与现有方法相比，该方法不要求未知参数为线性可参数化，从而使跟踪误差可减小到任意小值。该控制方法减小了超调量，快速实现跟踪，并且具有一定的抗干扰能力，显著提高了柔性关节机械手的控制稳定性。

附图说明

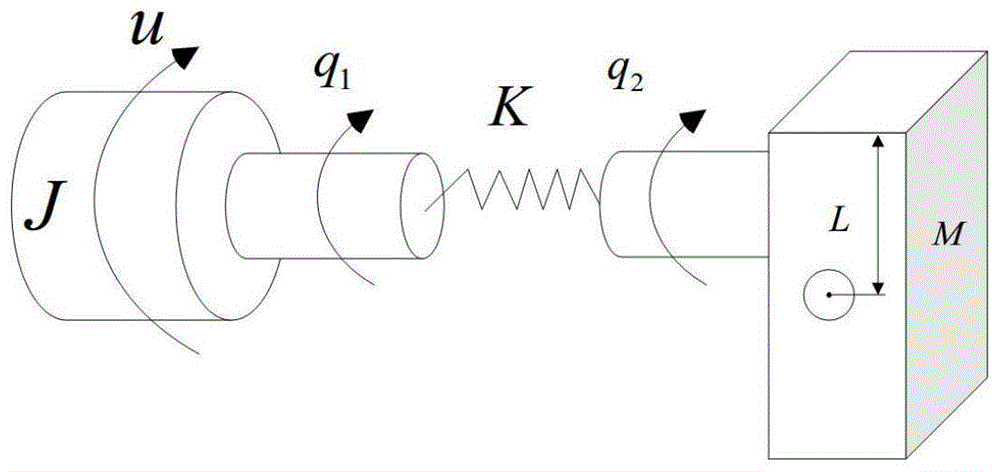
附图1为柔性关节机械臂模型示意图；

附图2为it2fnn逼近器的结构示意图。

具体实施方式

本发明提出了一种基于it2fnn逼近器的柔性关节机械臂自适应反演控制方法。利用李雅普诺夫稳定性理论，保证闭环系统中的所有信号最终都是有界的。与现有方法相比，该方法不要求未知参数为线性可参数化，跟踪误差可减小到任意小值。本文的主要贡献如下:1)针对具有不匹配不确定性的柔性关节机械臂，提出了一种基于it2fnn逼近器的自适应反演控制器。2)该控制器不仅能保证机械手系统的稳定性，而且能保证闭环系统中所有信号的有界性。3)通过与t1fnn和神经网络逼近器的比较，证明了该控制器对不确定柔性关节机械臂的期望轨迹跟踪的优越性。

本发明技术可以用以满足柔性关节机械臂对鲁棒控制技术的高精度要求。针对不确定非线性系统的具有模糊逼近器的自适应控制，近年来引起了研究人员的广泛关注。随着zadeh(1965)提出的模糊集理论的出现，模糊系统被证明是研究一类复杂非线性控制问题的有效方法。kayacan等人提出了基于最优滑模控制理论的算法对隶属函数进行优化的t1fnn和t2fnn。在许多应用中，t2fnn被证明具有比t1fnn和神经网络更好的处理不确定性的能力。然而，t2fnn降型中的迭代k-m算法计算量大、耗时长，难以应用于实际应用。还提出了用α平面的来表示的中心降型，这种方法有效地用于广义二型模糊集。这种改进的方法被应用于直接/间接自适应控制设计了一类不确定非线性系统。然后bibi等提出了用自适应因子α连接区间二型模糊系统中的yl和yr，以此取代km算法。自适应因子提高了算法的实用性。因此，在本文中，自适应因子α给了我们一个巨大的灵感,应用于具有不匹配不确定性的柔性关节机械手的基于it2fnn逼近器的自适应反演控制。

实施例1：

步骤一：建立柔性关节机械臂系统动力学模型：

图1中展示了单连杆柔性关节机械臂的简单模型。我们作如下假设。它的关节只能在关节旋转方向的垂直平面内，由于旋转产生变形。柔性关节机械臂的工作机理是电机轴和刚性连杆分别由电机和弹簧驱动来驱动。同时假设粘滞阻尼可忽略以及状态可测，它的动力方程可写成：

其中q1∈rⁿ和q2∈rⁿ分别是柔性关节连杆角位移和电机位移，和分别是柔性关节连杆角加速度和电机加速度，g是重力加速度，k是关节的弹簧刚度，u∈rⁿ是由电动机提供转矩的外部输入，i和j分别是柔性关节连杆与电机的转动惯量，m是柔性关节连杆的重量，l是机械臂重心与柔性关节之间的长度。

我们定义x1＝q1，x3＝q2和则公式(1)可写成如下状态空间表达式：

其中xi∈rⁿ,i＝1,2,3,4是状态变量，x1＝q1是连杆角位移，是连杆角速度，x3＝q2是电机位移，是电机速度，y＝x1是连杆角位移。考虑一个具有不匹配不确定性的单连杆柔性关节机械臂，以上模型无法使用。由于机器人基本上是由电机通过扭簧驱动的连杆，我们可以将其表示为两个子系统的级联:连杆动力学和电机动力学。控制输入在描述电机动力学的子系统中，其输出通过弹簧和连杆动力学耦合到另一个子系统中。因此，我们可以将公式(1)写成如下简化等式：

显然，g(x)＝-x3-mglsin(x1)/i-k(x1-x3)/i，f(x)＝k(x1-x3)/j，m＝1/j。我们假设g(x)、f(x)和m是未知的，但是m的下界是已知并满足m≥m和m＞0。

参见如下文献：huang,a.c,chen,etal.adaptiveslidingcontrolforsingle-linkflexible-jointrobotwithmismatcheduncertainties[j].controlsystemstechnologyieeetransactionson,2004,12(5):770-775。

区间二型模糊神经网络逼近器：

以下为一个高精度和鲁棒性的it2fnn逼近器。图2展示了it2fnn的结构。通过利用上下隶属函数，it2fnn在解决不确定性和逼近未知非线性函数有着明显的优势。it2fnn可以看成由两部分组成：一部分是包括if-then规则，另一部分是模糊推理机。

在it2fnn逼近器中，每条规则是以下形式：

其中x1,x2,…,xn是输入变量和y是输出变量。n是模糊规则总数。是区间二型模糊前件。代表二型模糊集的上下单值后件。每个数学函数符号描述如下。

对于一个输入向量x＝[x1,x2,…,xn]，利用单值解模糊，第k条规则的激活区间的上下界如下：

其中：

其中和分别是上下隶属函数。降型将区间类型2模糊集转换为区间集。最后，解模糊器将区间集转换为清晰的输出。

现在有很多种关于区间二型模糊集降型的方法。最常用的方法是中心降型法，具体形式如下：

其中yl和yr的计算如下：

其中θ＝[θ1,θ2,…,θn]和是二型模糊集的上下单值后件，ξ(x)＝[ξ¹,ξ²,…,ξ^k]和是基函数的向量，计算如下：

k-m和eiasc迭代算法可以确定一些用于连接上输出yr和下输出yl的交叉点。但是这种迭代计算过程将会耗费很多时间。自适应因子α在yr和yl中建立自适应调节过程，可以解决这样迭代计算中耗时多和精度低的问题[56]。

解模糊后的的计算如下：

将公式(8)和(9)代入(11)中，可得：

步骤二：将柔性关节机械臂期望的关节和电机的位移、角速度作为基于模糊神经网络逼近器的自适应反演控制器的参考输入，将电动机提供转矩的外部输入作为自适应反演控制器的实际输入，如果自适应反演控制器的实际输出值和预设期望值产生跟踪误差，该跟踪误差通过自适应反演控制器的迭代计算趋近于零。

在反演过程中，虚拟控制器x1d,i＝2,…,m在每一步的递推中是使得ei-1＝xi-1-x(i-1)d尽可能小。实际控制器u中包括最后的虚拟控制器x1d。实际控制器u是尽可减小xi和xid的误差。控制器的设计被分为以下几步。

步骤1：定义e1＝x1-x1d并且x1d＝yd，可得：

定义e2＝x2-x2d以及虚拟控制器x2d：

其中k1是一个非负的常数。

则公式(13)可写成：

选择如下李雅普诺夫函数：

对v1时间求导可得：

若e2＝0，则

步骤2：对e2＝x2-x2d时间求导，可得：

定义e3＝x3-x3d和虚拟控制器x3d：

其中k2是一个非负常数以及是g的估计值。

从公式(14)可得，对x2d求导可得：

从公式(18)以及(19)，对求导可得：

选择如下李雅普诺夫函数：

对v2时间求导可得：

如果e3＝0并且则

步骤3：对e3＝x3-x3d求导可得：

从公式(18)，(19)，(20)以及(22)，对x3d求导可得：

我们将分成两部分。是不含模型信息的已知部分和是包含模型信息的未知部分。则公式(25)可写成以下形式：

其中：

定义e4＝x4-x4d，以及虚拟控制器x4d。选择非负正数k3，可得：

将公式(26)-(29)代入公式(24)中，可得：

选择如下李雅普诺夫函数：

对v3时间求导可得：

如果e4＝0，以及则

步骤4：为了进行控制系统的稳定系分析，我们将在这步中构造实际控制器。对e4＝x4-x4d求导可得：

从公式(24)、(26)、(27)以及(29)，对x4d求导可得：

我们将分成两部分。是不含模型信息的已知部分和是包含模型信息的未知部分。则公式(34)可写成以下形式：

其中：

定义则公式(33)可写成：

其中是m的估计值。

选择如下控制律：

其中是h的估计值以及k4是非负常数。

将公式(39)代入(38)中，可得:

选择如下李雅普诺夫函数:

对v4时间求导可得:

如果以及则

自适应模糊控制部分：

我们用所提出的逼近器来逼近未知非线性函数g(x)、d(x)和h(x)，其中和是它们的估计值。

将所提出的自适应因子代入g(x)、d(x)和h(x)，可得:

其中εg(x)和εd(x)和以及εh(x)和是逼近误差；ξg(x)和ξd(x)和以及ξh(x)和分别是下隶属函数和上隶属函数；和和以及和分别是g(x)、d(x)和h(x)的下最优逼近参数和上最优逼近参数；αg、αd和αh是自适应因子。

根据所提出的逼近器，非线性函数和可以表示成

从公式(43)到(48)，可得:

其中和

将自适应律选为非线性函数可表示为：

其中初始值

自适应参数的自适应变化律选作以下形式：

其中是非负的自适应增益。

稳定性证明部分：

这时候，可以将我们主要的结果概括在以下理论中，在其中说明了所设计的控制器不仅保证了闭环系统的有界性和稳定性。

定理1：考虑公式(3)所示的柔性关节机械臂系统，公式(39)中的控制输入u和公式(52)到(58)中的基于it2fnn的自适应律保证了所有信号在闭环系统中是有界的。而且，对于给定的衰减系数ρ＞0，跟踪性能指标满足：

定理1的证明：

为了使证明过程更简洁，我们定义m(x)、g(x)、d(x)和h(x)为f1(x)、f2(x)、f3(x)和f4(x)。显然，m(x)、g(x)、d(x)和h(x)的逼近值分别是和

选择如下李雅普诺夫函数：

对v求导可得：

将公式(52)代入，可得：

将公式(49)-(51)代入，可写成：

令代入公式(53)-(58)，则可得：

假定可得：

因为可得：

因为以及可得:

因为我们可以得出则李雅普诺夫函数v的时间导数为：

为了满足我们定义ci,i＝1,…,4为非负常数以及则李雅普诺夫函数v的时间导数可写成：

进行如下定义：

则可得：

对上式在[0,t]内进行积分，有：

定义紧集ω0＝{x|v(x)≤c0}，其中则闭环系统所有信号有界。

定义则公式(68)可写成：

其中

对公式(73)在[0,t]内进行积分，可得：

因为有：

因为可得：

对于给定的衰减系数ρ＞0，跟踪效果的精度取决于逼近误差的上界。至此，证明完毕。

仿真结果表明，采用本发明方法的该控制器的跟踪误差可减小到任意小值，跟踪性能优于基于1型模糊神经网络(t1fnn)逼近器和神经网络(nn)逼近器的自适应反演控制器。

在这节中，我们将证明所提用于柔性关节机械臂的控制方法的有效性。

在公式(3)中动态方程的参数实际值为m＝0.2kg、l＝0.02m、i＝1.35×10^-3kg·m²、k＝7.47n·m/rad以及j＝2.16×10^-1kg·m²。三个it2fnn用于逼近未知函数g(x)、d(x)和h(x)。x＝[x1,x2,x3,x4]是输入向量。对于每个输入xi，选择如下二型高斯隶属函数：

其中i＝1,2,3,4、j＝1,2,3、c＝[c1,c2,c3]＝[1.25,0,-1.25]、σ＝[σ1,σ2,σ3]＝[0.6,0.6,0.6]和a＝0.8。

其他参数的选择如下：m＝1、和

相关初始值设置为：x(0)＝[x1(0),x2(0),x3(0),x4(0)]＝[0,0,0,0]、和期望跟踪轨迹为yd＝0.2sin(t)。控制目标是，即使在外部干扰d(t)＝0.05cos(2t)下，系统输出也能跟踪上期望轨迹。

在外部干扰d(t)＝0.05cos(2t)下的仿真结果证明了即使在外部干扰下，采用本发明方法的控制器有着更好的跟踪性能和更高的逼近精度。

为了评估不同逼近器(t1fnn,nn,it2fnn)的控制器的跟踪性能，我们用以下性能指标：误差平方的积分(ise)、误差绝对值的积分(iae)和误差绝对值与时间乘积的积分(itae)，具体公式如下：

表格i性能指标

表格i列举了所有控制器的ise、iae和itae的值。从中可发现，相比于tifnn和nn逼近器的控制器，采用本发明方法的控制器在参考轨迹跟踪上有着更好的性能。