基于四元数的冗余机械臂抗推绕姿态控制方法与流程

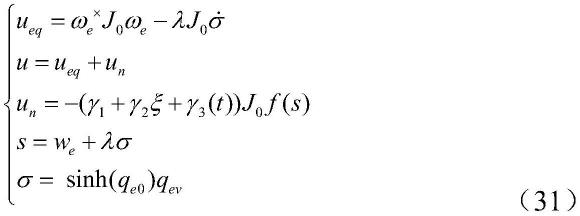
1.本发明属于机械臂控制技术领域，涉及基于四元数的冗余机械臂抗推绕姿态控制方法。


背景技术：

2.由于指向精度高、快速响应、鲁棒性强等机械臂控制任务的要求越来越具有挑战性，机械臂控制器设计已成为研究热点。多自由度为冗余操纵器创造了核心优势，以实现比非冗余操纵器更复杂的任务。由于这种冗余性，冗余机械手得到了广泛的研究，包括避障、重复运动产生和合作运动产生等方面的深入研究。冗余机械手的许多成就和功能已经实现并应用于服务和制造业。冗余机械手的冗余分析相当于一个优化问题，因为对于一个给定的任务来说，冗余分析具有无限的解决属性。
3.优化问题的建模方法和解决策略直接决定了机械手的功能和效率。现有的文章针对机械臂控制问题，提出了各种控制方案，如比例积分微分(pid)控制律、线性参数变化(lpv)增益调度控制器、模糊控制方法等。尽管有了这些成效，冗余机械臂的姿态机动控制仍然具有挑战性。滑动模式控制(smc)是一种非线性控制技术，它通过应用不连续控制律(或更严格地说，是集值控制信号)来改变非线性系统的动力学，该控制律迫使系统沿着系统正常行为的横截面滑动。这种控制技术首次被提出用于可变结构系统。随后，由于其较强的鲁棒性，它在处理机械臂控制方面引起了广泛的关注。由于不连续符号函数的存在，传统的smc控制器存在颤振问题。为了减轻这种不良的性能，符号函数被近似为饱和函数。在已有文章中，引入了一个边界层来解决抖振问题，将不连续符号函数引入到控制输入的一阶导数中，然后给出了一个无颤振的高阶积分smc。此外，smc技术还与其他控制方法相结合，可以提高自适应控制方法等机械臂姿态控制系统的性能。
4.上述方法的一个典型特征是，当用四元数描述机械臂姿态时，其优点是无奇异，无超越函数运算，可用于连续旋转表示，但是缺点为存在一个冗余，存在退绕现象，不直观。四元数具有双覆盖性质，因此对于刚体的给定物理姿态有两种数学表示。因此，存在两个平衡点[1 0 0 0]
t
和[-1 0 0 0]
t
。然而，在传统的控制律设计中，只考虑了一个平衡点。在这种情况下，系统状态必须移动到所考虑的平衡点，即使它们非常接近另一个平衡点。这被称为展开现象，当一个小角度机动足以达到控制目标时，它可能会导致机械臂进行不必要的大角度机动。据研究发现，关于机械臂展开问题的研究很少。在有关航天器的研究中，在滑动表面中引入sign(q0(0))以避免展开现象。将(1-|q0|)设计为姿态误差。在这种情况下，考虑了平衡点[1 0 0 0]
t
和[-1 0 0 0]
t
。但没有严格地证明所设计的控制器如何避免展开现象，也没有应用到机械臂上。


技术实现要素：

[0005]
为了克服上述现有技术的不足，本专利提出了一种基于四元数的冗余机械臂抗推绕姿态控制方法,进而保证机械臂闭环系统在边界层内的反展开性能和收敛性。
[0006]
本发明所采用的技术方案是：
[0007]
步骤1，利用四元数方法对电缆机械臂建立数学模型；
[0008]
步骤2，基于姿态动力学进行误差设计，获得误差四元数；
[0009]
步骤3，通过双曲正弦函数设计了一个新的基于误差四元数的开关函数，使开关面包含两个平衡点；
[0010]
步骤4，基于所提出的开关函数开发了一个滑动模式姿态机动控制器，以确保闭环系统对扰动和惯性不确定性的鲁棒性。
[0011]
进一步的，步骤1的具体实现方式如下；
[0012]
微分运动学给出了关节速度与相应的端效应器线速度和角速度之间的关系，机械臂的微分运动学方程可表示为：
[0013][0014]
其中表示车身帧fb相对于惯性帧fi的姿态，上面带
·
的表示求导数，q0为四元数的标量部分，qv为四元数的矢量部分，i3为3*3的单位矩阵，表示fb的角速度；为机械臂的惯性矩阵，u为作用于主体上的控制力矩，d为外部扰动；对于任何向量m＝[m1,m2,m3]
t
，m
×
表示一个偏对称矩阵，可以由公式(2)得出：
[0015][0016]
进一步的，步骤2的具体实现方式如下；
[0017]
姿态误差设计：设为期望帧fd相对于惯性帧fi的机械臂姿态，设为期望帧fd的机械臂角速度，姿态误差设由以下公式设计为
[0018][0019]
其中其中是是四元数乘法算子；此外，因为因此有
[0020][0021]
根据(4)，误差四元数qe的分量为：
[0022][0023][0024]
通过对(5)的导数，得到了以下姿态误差运动学：
[0025]
[0026]
其中，表示角速度误差，并由
[0027]
ωe＝ω-rωdꢀꢀꢀ
(7)
[0028]
其中r为从fd到fb的相对旋转矩阵，有
[0029][0030]
旋转矩阵r满足从(7)得出
[0031][0032]
姿态误差动力学：对于一个静止到静止的姿态机动控制问题，所期望的姿态速度满足ωd＝0,因此，它可以从(7)中得到ωe＝ω，考虑到这一点，通过将(7)和(9)代入(1)的第二个方程，可以得到以下姿态误差动态方程，
[0033][0034]
此外，考虑惯性不确定度，即j＝j0+δj，其中j0是表示标称部分的常数矩阵，δj为不确定度部分，(10)被转化为
[0035][0036][0037]
然后，通过(6)和(11)，设计相对姿态误差的姿态动力学方程为，
[0038][0039]
此外，误差四元数也可以写成：
[0040][0041]
其中，θ(t)∈[0,2π]为旋转角，为欧拉轴，然后，从(14)的第一个关系中可以推导出以下关系，
[0042]
θ(t)＝2arccos q
e0
ꢀꢀꢀ
(15)
[0043]
从(4)和(13)的第一个关系中可得出：
[0044][0045]
根据(3)，只要给出q的初始姿态q(0)和期望的姿态qd，就可以得到q
e0
(0)和q
ev
(0)；此外，θ(t)的初始值θ(0)可以通过上式得到，设计的姿态机动控制器的目的是驱动机械臂绕欧拉轴e旋转，使旋转角度θ(t)从初始值θ(0)收敛到平衡点。
[0046]
进一步的，步骤3中设计的开关函数如下；
[0047]
s＝we+λσ
ꢀꢀꢀ
(17)
[0048]
其中λ为正常数，并且
[0049]
σ＝sinh(q
e0
)q
ev
ꢀꢀꢀ
(18)
[0050]
函数cosh q
e0
和具有的性质：当q
e0
＝1和q
e0
＝-1时，可以得到函数cosh q
e0
的最大值，对于θ(t)∈(0,π]，有而对于θ(t)∈(π,2π)，有sinh cosθ(2t)＜0。
[0051]
进一步的，步骤5中需要构造一个控制律，即滑动模式姿态机动控制器，使其满足条件ss
t
＜0，这一条件保证了开关面s＝0将吸引所有的系统轨迹；
[0052]
根据机械臂的姿态误差动力学(13)的状态反馈控制，
[0053]
u＝u
eq
+unꢀꢀꢀ
(19)
[0054]
其中u
eq
为标称系统的等效控制，un用于补偿扰动和惯性不确定性，通过将un设置为0，可以从标称系统部分得到等效控制u
eq
，也就是说
[0055][0056]
其中，的表达式如下，
[0057][0058]
姿态误差动力学(13)的标称部分为：
[0059][0060]
控制项un的设计为：
[0061]
un＝-(γ1+γ2ξ+γ3(t))j0f(s)
ꢀꢀꢀ
(23)
[0062]
其中γ1和γ2为正数，ξ在(23)中给出，其中γ3(t)为正值函数，
[0063][0064]
然后，提出了以下抗推绕滑模姿态控制律：
[0065][0066]
其中λ、γ1和γ2为正数，则σ、ξ和f(s)已分别给出，而g＝sinh(q
e0
)||q
ev
||。
[0067]
与现有技术相比，本发明具有以下有益效果：
[0068]
本发明能避免退绕现象，并对扰动和惯性的不确定性进行了补偿，消除了震颤振问题，更适用于实际工程应用。本发明提出了一个包含两个平衡点的新的开关函数，通过选择一个由双曲余弦函数构造的李雅普诺夫函数，证明了系统状态在开关面上时的反展开性能。其次，设计了滑模控制律，保证系统轨迹被切换面吸引。此外，通过设计一个滑模控制律的动态参数，证明了当系统状态在开关面外时的反展开性能。第三，通过为开关表面引入边界层来避免颤振现象，如果选择所设计的开关面的参数来满足一定的条件，可以保证机械臂闭环系统在边界层内的反展开性能和收敛性。
具体实施方式
[0069]
下面结合具体实施步骤对本发明的技术方案做进一步详细的说明。
[0070]
步骤一，利用四元数对系统模型进行建模，以及用数学合理表达要解决的问题
[0071]
1.1系统模型
[0072]
微分运动学给出了关节速度与相应的端效应器线速度和角速度之间的关系，机械臂的微分运动学方程可表示为
[0073][0074]
其中表示体框架fb相对于惯性帧fi的姿态，表示fb的角速度；为机械臂的惯性矩阵(对称)，u为作用于主体上的控制力矩，d为外部扰动；
[0075]
此外，对于任何向量m＝[m1,m2,m3]
t
，m
×
表示一个偏对称矩阵，可以由公式(2)得出：
[0076][0077]
基于姿态动力学，下一节给出了自身框架fb和期望框架fd之间的相对姿态误差的运动学和动力学。
[0078]
姿态误差设计：设为期望帧fd相对于惯性帧fi的机械臂姿态。设为期望帧fd的机械臂角速度，姿态误差设由以下公式设计为
[0079][0080]
其中其中是是四元数乘法算子。此外，因为因此有
[0081][0082]
根据(4)，误差四元数qe的分量为：
[0083][0084][0085]
通过对(5)的导数，我们得到了以下姿态误差运动学
[0086][0087]
其中，表示角速度误差，并由
[0088]
ωe＝ω-rωdꢀꢀꢀ
(7)
[0089]
其中r为从fd到fb的相对旋转矩阵，由
[0090][0091]
旋转矩阵r满足从(7)得出
[0092][0093]
姿态误差动力学：对于一个静止到静止的姿态机动控制问题，所期望的姿态速度满足ωd＝0,因此，它可以从(7)中得到，ωe＝ω持有。考虑到这一点，通过将(7)和(9)代入(1)的第二个方程，可以得到以下姿态误差动态方程，
[0094][0095]
此外，本文考虑了惯性不确定度，即j＝j0+δj，其中j0是表示标称部分的常数矩阵，δj为不确定度部分。(10)被转化为
[0096][0097][0098]
然后，通过(6)和(11)，相对姿态误差的姿态动力学为，
[0099][0100]
此外，误差四元数也可以写成
[0101][0102]
其中，θ(t)∈[0,2π]为旋转角，为欧拉轴。然后，从(14)的第一个关系中可以推导出以下关系，
[0103]
θ(t)＝2arccos q
e0
ꢀꢀꢀ
(15)
[0104]
从(4)和(13)的第一个关系中可以得出
[0105][0106]
根据(3)，只要给出q的初始姿态q(0)和期望的姿态qd，就可以得到q
e0
(0)和q
ev
(0)。此外，θ(t)的初始值θ(0)可以通过上式得到。通过设计一种姿态机动控制器，驱动机械臂绕欧拉轴e旋转，使旋转角度θ(t)从初始值θ(0)收敛到平衡点。
[0107]
1.2退绕现象
[0108]
鉴于机械臂内部关系，有q
e0
|
θ(t)＝0
＝1和q
e0
|
λ(t)＝2π
＝-1两个平衡位置。在物理旋转空间中，θ(t)＝0和θ(t)＝2π表示相同的期望位置。因此，q
e0
＝1和q
e0
＝-1都是机械臂的姿态误差动力学的平衡点。然而，在大多数现有的控制器设计方法中，只有q
e0
＝1被认为是一个平衡点。在这种情况下，对于一个静止到静止的姿态机动控制问题，当初始值q
e0
小于0时，设计的控制器驱动q
e0
到0，最后驱动到1。这意味着刚性航天器需要旋转一个大于π的角度θ(t)。这就是“退绕现象”。然而，机械臂可以通过旋转一个小于π的角度来达到所需的姿态。
[0109]
1.3控制目标
[0110]
本工作的控制任务是设计一种抗退绕姿态控制器，以实现机械臂的静止-静止姿态操纵。通过采用设计的控制律，对于机械臂的闭环姿态机动误差动力学，实现以下关系：
[0111][0112][0113]
此外，在机械臂机动过程中，避免了退绕现象。
[0114]
步骤二，针对要解决的问题，设计合适的滑膜面和控制方案
[0115]
2.1开关滑膜面
[0116]
对于机械臂的姿态误差动力学，我们设计了以下开关函数
[0117]
s＝we+λσ
ꢀꢀꢀ
(18)
[0118]
其中λ为正常数并且
[0119]
σ＝sinh(q
e0
)q
ev
ꢀꢀꢀ
(19)
[0120]
然后，给出了一个定理，证明当系统状态限制在开关面s＝0时，实现了控制目标。在给定这个定理之前，我们应该给出函数cosh q
e0
和的一些性质。当q
e0
＝1和q
e0
＝-1时，可以得到函数cosh q
e0
的最大值。对于θ(t)∈(0,π]，有而对于θ(t)∈(π,2π)，有sinh cosθ(2t)＜0。
[0121]
理论2：如果姿态误差动力学的系统状态仅限于开关面s＝0，则可以得出以下结论。
[0122]
(i)角速度误差ωe收敛于0，q
e0
收敛于1或-1。
[0123]
(ii)避免了退绕现象。
[0124]
证明：首先，我们选择以下的李雅普诺夫函数。
[0125]v1
(t)＝2(κ-cosh q
e0
)
ꢀꢀꢀ
(20)
[0126]
其中κ＝max(cosh q
e0
)且q
e0
∈[-1,1]，通过取(20)的时间导数，并使用上述方程，条件s＝0，我们有
[0127][0128]
显然此外，从(20)和(21)可知，如果则存在q
e0
＝0或q
ev
＝0。将此与(4)结合起来，我们得到了
[0129][0130]
此外，还可以从(22)中得到：
[0131][0132]
此外，对于任何较小的正值ε，它可以从(23)得到从上述方程式中的关系可知，开关面的＝0包含两个平衡点q
e0
＝1或q
e0
＝-1，即或-1。另外，将q
ev
＝0代入(20)中，得到ωe＝0。因此，证明了结论(i)。
[0133]
接下来，证明了系统状态在开关表面s＝0上的姿态误差动力学的反展开性能。根据(15)，李亚普诺夫函数可以转化为
[0134][0135]
且可以得到
[0136]
这意味着当系统状态被限制在开关面s＝0时，避免了展开现象。
[0137]
2.2姿态控制律
[0138]
在本节中，我们需要构造一个控制律，使其满足条件ss
t
＜0。这一条件保证了开关面s＝0将吸引所有的系统轨迹。
[0139]
考虑一类针对刚性航天器的姿态误差动力学(13)的状态反馈控制，
[0140]
u＝u
eq
+un(25)
[0141]
其中u
eq
为标称系统的等效控制，un用于补偿扰动和惯性不确定性。通过将un设置为0，可以从标称系统部分得到等效控制u
eq
。也就是说
[0142][0143]
其中，可以得到如下，使用(21)和(13)的第一个关系，
[0144][0145]
姿态误差动力学(13)的标称部分为
[0146]
[0147]
控制项un的设计为
[0148]
un＝-(γ1+γ2ξ+γ3(t))j0f(s)
ꢀꢀꢀ
(29)
[0149]
其中γ1和γ2为正数，ξ在(29)中给出，γ3(t)是一个正值函数，
[0150][0151]
然后，提出了以下抗推绕滑模姿态机动控制定律
[0152][0153]
其中λ、γ1和γ2为正数，则σ、ξ和f(s)已分别给出，而g＝sinh(q
e0
)||q
ev
||。
[0154]
2.3收敛性分析
[0155]
在本节中，首先给出定理3，分析了闭环系统在定律下当系统状态在滑动面之外时的收敛性能和反展开特性。此外，通过在式中引入不连续函数f(s)的边界层，提出了具有连续控制体系结构的机械臂抗推绕姿态控制定律。此外，给出了定理4，说明了该系统在连续奥斯马克定律下，该系统在边界层内的无展开性和收敛性。
[0156]
定理3：考虑在假设下描述的机械臂和提出的ausmamc定律。我们得出了以下结论。
[0157]
(i)开关函数s在有限时间内收敛于0。
[0158]
(ii)如果选择提议的标准定律的参数γ3(t)为
[0159][0160]
其中g＝sinh(q
e0
)||q
ev
||以及然后，在系统状态达到开关面s＝0之前，避免了展开现象。
[0161]
证明：为了证明结论(i)，我们选择了以下李亚普诺夫函数
[0162][0163]
在上述帮助下，我们从(33)中可得
[0164][0165]
将奥斯曼克定律替换(34)，为
[0166][0167]
从(30)得出，||s||≠0时存在以下关系
[0168][0169]
通过将其与上述结合起来，很容易得到
[0170][0171]
显然，进一步地，根据引理1，s在有限时间内收敛于0。因此，(i)被证明。
[0172]
接下来，通过设计动态参数γ3(t)，保证了系统状态达到开关面s＝0之前的反展开性能。
[0173]
鉴于上式，可推导出
[0174][0175]
假设初始时间为t0＝0。然后，通过取(38)两边的积分，我们就得到了
[0176][0177]
直接计算给出
[0178][0179][0180]
从上述关系中可以得出
[0181][0182]
注意，是一个单位向量。然后，矩阵是一个幂等矩阵。因此，我们有从(42)中可以得出
[0183][0184]
结合上述，得出
[0185]
[0186]
此外，还可转化为
[0187][0188]
需要注意的是，本文考虑了静止到静止的姿态机动问题。因此，ωe(0)＝0。此外，它可以从(16)得到然后，可以得到(45)中的v(t)的初始值为
[0189]
v(0)＝λg(0)
ꢀꢀꢀ
(46)
[0190]
此外，在上述的帮助下，我们得到v2(0)的初始值为(ωe(0)＝0)
[0191][0192]
因此，可以从已知式子中得出以下关系
[0193][0194]
这可以进一步写成
[0195][0196]
假设t
s0
是系统状态到达滑动面s＝0的时间，即根据(47)中的v(t)＝0。为了证明t∈[0,t
s0
]的闭环系统的反展开特性，我们需要证明如果θ(0)∈(0,π]且时，t∈[0,t
s0
]成立；如果θ(0)∈(π,2π]时，t∈[0,t
s0
]为此目的，我们将考虑以下两种情况来完成证明。
[0197]
(a)当θ(0)∈(0,π]时，通过(14)的第一个方程，我们有q
e0
(0)＞0。然后，使用(51)，我们得到
[0198]
v(0)＝λsinh(q
e0
(0))||q
ev
(0)||＞0
ꢀꢀꢀ
(50)
[0199]
因此，对于t∈[0,t
s0
]，就有v(t)≥0。在这种情况下，它可以从(50)进一步得出
[0200][0201]
可以进一步转化为
[0202][0203]
如果那么它从(32)得出结合(52)，可得出
[0204][0205]
(b)当θ(0)∈(π,2π)时，通过已知方程，我们有q
e0
(0)＜0。通过推导可得到v(0)＝λsinh(q
e0
(0))||q
ev
(0)||＜0
ꢀꢀꢀ
(54)
[0206]
因此，对于t∈[0,t
s0
]，就有v(t)≤0。在这种情况下，(54)可以重写为
[0207][0208]
同理可得
[0209][0210]
可知这意味着在系统状态到达开关面＝0之前，在奥斯曼定律下，使用控制率成功地避免了展开现象。
[0211]
在定理3(ii)中，在系统状态到达开关面之前，已经证明了其反展开性能。在定理2(ii)中，当系统状态在开关表面上被收缩时，其反展开性能也得到了证明。这两个定理的结果表明，闭环系统(13)根据该定律(36)和(35)具有反展开的性能。
[0212]
备注2：所提出的机械臂抗推绕姿态控制的一个缺点是它对开关面的＝0是不连续的。这种特性可能会引起不希望出现的颤振现象。对于实际的实现，控制器必须被平滑处理。因此，为其中函数f(s)的s＝0引入了一个边界层ε，从而使
[0213][0214]
其中，ε是一个很小的正值。当ε趋近于零时，该边界层的性能可以任意地接近于原
始控制律的性能。
[0215]
因此，根据定理3，以下结论适用于ausmamc定律。
[0216]
(i)(20)中的开关函数s在有限时间内收敛于边界层||s||＞ε，其中λ是一个很小的正值。
[0217]
(ii)如果选择参数γ3(t)为(32)，则在开关函数s收敛到边界层||s||≤ε之前，避免了展开现象。下面给出了一个定理，分析了封闭环系统在控制器下的收敛性能和反展开特性。
[0218]
定理4：考虑||s||≤ε假设1下描述的机械臂，如果选择ausmamc定律的参数γ3(t)为(37)，且λ满足
[0219][0220]
其中ε和ε1为较小的正数，则避免了展开现象。此外，ωe和qev分别收敛于区域和区域，其中
[0221][0222][0223]
证明：根据(50)、(58)和||s||≤ε的关系，我们得到了
[0224][0225]
此外，考虑到(38)和(14)，我们有
[0226][0227]
然后考虑以下情况来完成证明。
[0228]
如果为θ(t)∈(0,π)，θ(t)∈(π,2π)因此，θ(t)增加到2π-ε1。可以得出结论，即和此外，使用上述式子得到
[0229][0230]
因此，所提出的机械臂抗推绕姿态控制能避免退绕现象，并对扰动和惯性的不确定性进行了补偿。此外，该方法消除了震颤振问题，更适用于实际工程应用。