基于线性回归算法的家用净水器可预测更换时间的方法与流程

本发明涉及人工智能技术领域，尤其涉及一种基于线性回归算法的家用净水器可预测更换时间的方法。

背景技术：

随着人们生活水平的提高，以及对环境污染的重视，家用净水器逐渐得到普及。在家用净水器得使用过程中，过滤滤芯起到至关重要的作用，净水器的滤芯能有效地清除市政供水中的重金属、水碱、杂质颗粒、细菌、抗生素、病毒、于氯等对人体有害的物质，使得经过净水器处理的的水质安全可靠。但是，净水器的滤芯是有使用寿命也就是处理水总量的，在正常的情况下，一旦净水器的滤芯达到使用寿命而不更换，经过其处理的水会携带大量的细菌等对人体有害的物质。目前，对于滤芯的更换，一般采用的的方法是使用年限或机械式监测提醒，但是，市政供水水质受当地水质和市政供水管网的影响特别大，采用传统的使用年限和机械式检测提醒方法不能及时监测滤芯是否已经超过使用寿命。

中国专利公开号cn105540901a公布了一种智能净水系统，该方案包括用于控制智能净水系统工作的主控制板、用于检测原水和通过活性炭单元后的水的余氯浓度的orp检测单元、用于检测水质的tds值检测单元、用于检测水流量的流量传感器单元、用于控制冲洗pvdf超滤膜的膜自动冲洗单元组成；主控制板上设置有orp检测控制模块、tds值检测模块、流量检测模块、膜自动冲洗控制模块、无线通讯模块和显示屏控制模块。该方案智能净水系统能显示滤材使用剩余状态及水质数据信息，便于用户了解清洗或更换滤材的情况。该方案虽然能实现滤芯更换的提醒，但都是以机械式方式实现的，因各地水质差异，所以滤芯更换提醒并不准确。

净水器是对水质进行深度过滤、净化处理的水处理设备。平时所讲的净水器，一般是指用作家庭使用的小型净化器。家中的自来水通常经过：自来水厂处理——管道输送——小区水箱——管道输送——入户。自来水入户后到饮用需经过：前置过滤器——中央净水机——末端净水器。大部分的家庭会安装末端净水器，其技术核心为滤芯装置中的过滤膜，目前主要技术来源于超滤膜、ro反渗透膜、纳滤膜三种。传统净水器一般有三级滤芯，用于过滤颗粒物等物质。净水器的内部管路设计滤芯前松后紧，由pp熔喷滤芯、颗粒碳、压缩碳、ro反渗透膜或超滤膜、后置活性炭等，三层滤芯依次首尾相连组成。过滤后剩余截留物沉积于滤芯内部，需要定期人工拆洗，以确保机器正常运作。普通家庭在喝饮用水的同时，最担心的问题就是不清楚净水机的滤芯是否干净，也不清楚什么时候需要更换，但是净水器滤芯的更换问题一直没有明确的标准。

鉴于上述问题，本发明公开了一种基于线性回归算法的家用净水器可预测更换时间的方法，建立一个不同水源，不同处理过程或过滤级别、不同的水温下的模型，用于精确提醒用户及时更换滤芯，保证用水健康。

技术实现要素：

本发明的主要目的就是针对以上存在的问题及限制，提供一种基于线性回归算法的家用净水器可预测更换时间的方法。

为了实现上述目的，本发明公开了一种基于线性回归算法的家用净水器可预测更换时间的方法，包括以下步骤；

步骤1，获取预定的测量对象进行测量，得到记录数据，包括：通过对测量对象的检测，获取净水器的设置参数以及环境的各项参数。其中所述测量对象包括：净水器开关时间、进水温度、进水流量、当地水质多项指标(cod、bod、toc、tod等)、使用时长等；

步骤2，从步骤1获得的数据中获取预定时间段的用户历史数据；

步骤3，对步骤2获得的数据进行预处理得到包含环境信息的用户使用数据。对所述操作数据和环境数据进行清洗，删除或修正问题数据和错误数据，得到清洗后的数据，将其整理为符合神经网络输入结构的预处理数据；

步骤4，将步骤3获得的数据输入到预定的神经网络中并进行深度训练学习，生成个性化深度学习模型；

步骤5，将步骤4得到个性化深度学习模型对包含环境的用户数据进行预测，得到个性化预测的用户使用习惯；

步骤6，将步骤5个性化预测的用户使用习惯为依据，计算出净水器滤芯可用时间并在用户智能家居终端显示，提示用户滤芯剩余使用时间；

步骤7，重复步骤1至步骤6，不断从用户行为中获取新的操作数据，将新数据再次输入至神经网络进行训练，更新用户个性化预测模型，在此过程中不断提高对用户习惯预测的精准度，计算出净水器滤芯可用时间并并在用户智能家居终端显示。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤1中获取预定的测量对象是净水器滤芯相关数据，获取净水器的设置参数以及相关环境的各项参数。所述的预定时间段内的操作数据包括：净水器开关状态、进水温度、累计流量、多个水质指标等。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤2中，通过算法自动获取净水器滤芯的历史数据

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤3中，对历史数据进行预处理，滤除重复数据、异常数据、垃圾数据。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤4中，将处理后的数据输入到线性回归模型中，并对历史数据进行训练学习，生成个性化深度学习模型。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的骤5中，利用步骤4生成的深度学习模型，使用包含环境的用户数据进行预测，预测出净水器剩余可用时间。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤6中，以上述模型为依据，计算出净水器滤芯剩余的可用时间并显示在手机app上。

上述的基于线性回归算法的家用净水器可预测更换时间的方法，其中，所述的步骤7中，用户在下一使用周期中，对所述净水器运行参数进行调整产生新的净水器参数，所产生新的净水器参数作为新的历史数据加入上述预定时间段的历史数据中。

本发明的基于线性回归算法的家用净水器可预测更换时间的方法由于采用了上述方案，使之与现有技术相比，具有以下的优点和积极的技术效果：

(1)本发明的基于线性回归算法的家用净水器可预测更换时间的方法通过人工智能深度学习获取的数据能及时判断水质的好坏，一旦水质变差，会及时提醒用户更换滤芯或耗材，避免已经失去功效的滤芯或耗材继续使用造成的二次生活用水污染；

(2)本发明的基于线性回归算法的家用净水器可预测更换时间的方法为用户提供安全可靠的净水饮用水，保证了用户家用水质的安全。

(3)本发明的基于线性回归算法的家用净水器可预测更换时间的方法通过建立一个不同水源、不同处理过程或过滤级别、不同的水温下的模型，用于精确提醒用户及时更换滤芯，保证用水健康。

附图说明

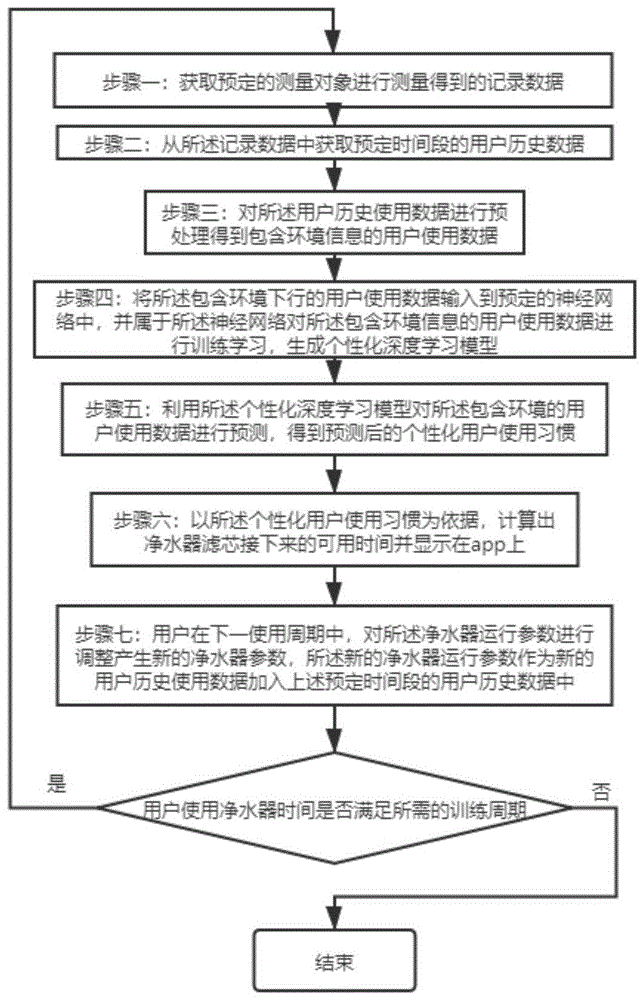
图1是本发明基于线性回归算法的家用净水器可预测更换时间的方法的工作流程图；

图2是本发明基于线性回归算法的家用净水器可预测更换时间的方法的梯度下降算法图；

图3是本发明基于线性回归算法的家用净水器可预测更换时间的方法的手机app端显示滤芯预计更换时间图。

具体实施方式

本发明的主要目的就是针对以上存在的问题及限制，提供一种基于线性回归算法的家用净水器可预测更换时间的方法。

请参见图1，本发明公开了一种基于线性回归算法的家用净水器可预测更换时间的方法，包括以下步骤；

步骤1，获取预定的测量对象进行测量，得到记录数据，包括：通过对测量对象的检测，获取净水器的设置参数以及环境的各项参数。其中所述测量对象包括：净水器开关时间、进水温度、进水流量、当地水质多项指标(cod、bod、toc、tod等)、使用时长等；

步骤2，从步骤1获得的数据中获取预定时间段的用户历史数据；

步骤3，对步骤2获得的数据进行预处理得到包含环境信息的用户使用数据。对所述操作数据和环境数据进行清洗，删除或修正问题数据和错误数据，得到清洗后的数据，将其整理为符合神经网络输入结构的预处理数据；

步骤4，将步骤3获得的数据输入到预定的神经网络中并进行深度训练学习，生成个性化深度学习模型；

步骤5，将步骤4得到个性化深度学习模型对包含环境的用户数据进行预测，得到个性化预测的用户使用习惯；

步骤6，将步骤5个性化预测的用户使用习惯为依据，计算出净水器滤芯可用时间并在用户智能家居终端显示，提示用户滤芯剩余使用时间；

步骤7，重复步骤1至步骤6，不断从用户行为中获取新的操作数据，将新数据再次输入至神经网络进行训练，更新用户个性化预测模型，在此过程中不断提高对用户习惯预测的精准度，计算出净水器滤芯可用时间并并在用户智能家居终端显示。

所述的步骤1中获取预定的测量对象是净水器滤芯相关数据，获取净水器的设置参数以及相关环境的各项参数。所述的预定时间段内的操作数据包括：净水器开关状态、进水温度、累计流量、多个水质指标等。

所述的步骤2中，通过算法自动获取净水器滤芯的历史数据

所述的步骤3中，对历史数据进行预处理，滤除重复数据、异常数据、垃圾数据。

所述的步骤4中，将处理后的数据输入到线性回归模型中，并对历史数据进行训练学习，生成个性化深度学习模型。

通过使用机器学习中的线性回归算法，通过累计流量、水温、多个水质指标等组成的训练集训练出的模型，将流速转换为天数，预测出当前用户所使用的末端净水器还有多长时间需要更换滤芯，并显示在用户界面上。

净水器滤芯剩余可用时间预测这个问题是一个回归问题，而这里影响的因素(变量)有多个，是一个多元回归问题。回归模型正是表示从输入变量到输出变量之间的映射的函数。回归问题分为两个过程，分别是学习和预测。

回归是基于已有数据对新的数据进行预测，线性回归就是能够用一个直线较为精确地描述数据之间的关系，这样当出现新的数据的时候，就能够预测出一个简单的值。利用已知的数据，(线性回归中需要找到一条直线)最大程度的拟合样本与输出标记，即产生拟合方程，从而对未知的数据进行预测。

首先是给定一个训练数据集：

t＝{(x⁽¹⁾，y⁽¹⁾，(x⁽²⁾，y⁽²⁾)，...，(x^(m)，y^(m))}

学习系统基于训练数据集构建一个模型(也叫预测函数)，即y＝f(x)，对新输入的x^(m+1)，预测系统过根据学习的模型y＝f(x)确定相应的输出y^(m+1)。

下面是我们约定的表示方式：

m代表训练集中样本的数量

x代表输入变量

y代表输出变量

(x,y)代表训练集中的样本

(x⁽ⁱ⁾，y⁽ⁱ⁾)代表第i个样本，如上述净水器中的一个数据，输入x(1)表示：(rooms：2，halls：1，size：50)，输出y(0)表示：price：170

代表第i个样本的第j个分量，举净水器流量数据为参考，表示第一个数据样本中的halls字段，即

净水器滤芯剩余可用时间预测实际上就是通过大量的训练数据来训练模型，最终得到预测函数y＝f(x)。然后我们将要预测的净水器的流量、水质等作为输入变量，然后通过学习得到的预测函数f(x)得到输出变量为结果。这里我们假设放假的预测函数为：hθ(x)＝θ0+θ1x1+θ2x2+θ3x3，x1、x2、x3分别代表输入变量，所以这里的问题就变成了求解θ0、θ1、θ2和θ3四个参数，找到符合的预测函数。

上面，我们假设了预测函数为：hθ(x)＝θ0+θ1x1+θ2x2+θ3x3。也就是说，我们要求解出θ0、θ1、θ2和θ3四个参数。但是得到参数解以后，我们怎么判定得到的参数是最合适的呢？这里就引用到代价函数的概念。我们知道通过预测函数得到的预测值f(x)和实际的值y是可能存在一定误差的，而我们要做的是就是缩小这些误差。下面我们构建一个代价函数，这个函数是所有建模误差的平方和，即：

其中hθ(x)＝θ0+θ1x1+θ2x2+θ3x3。所以，我们的目标就是找出使得代价函数最小的一系列参数变量θ0、θ1、θ2和θ3，代价函数返回的值越小，说明预测函数越拟合数据，当然也可能出现过拟合的情况。

梯度下降是一个用来求函数局部最小值的算法，相应地梯度上升算法是用来求函数局部最大值的算法。

请参见图2，该图是求通过梯度下降算法求j(θ0、θ1)的最小值，可以看到不同的初始值可能导致最终得到不同的局部最小值。

多元线性回归的批量梯度下降算法为：

在上式中α称为学习率，也叫步长，它决定了在梯度下降的迭代过程中，每一步沿梯度负方向前进的长度。以上图的例子，学习率就是这一步所在位置沿着最陡峭的最易下山的位置走的那一步的长度。学习率如果取值太小，会导致收敛变慢，迭代次数变多；取值太大，则会导致波动较大，导致无法收敛。同时，该算法要对所有的θ参数变量进行求导过程。

因此梯度下降算法主要内容如下：

预测函数：hθ(x)＝θ0+θ1x1+θ2x2+θ3x3

参数：θ0、θ1、θ2、θ3

代价函数：

目标：minimizej(θ0，θ1，θ2，θ3)

梯度下降：

线性回归模型有很好的可解释性，可以从权重w直接看出每个特征对结果的影响程度。线性回归适用于x和y之间存在线性关系的数据集，可以使用计算机辅助画出散点图来观察是否存在线性关系。我们尝试使用一条直线来拟合数据，使所有点到直线的距离之和最小。

线性回归中通常使用残差平方和，即点到直线的平行于y轴的距离而不用垂线距离，残差平方和除以样本量n就是均方误差。均方误差作为线性回归模型的损失函数(costfunction)。使所有点到直线的距离之和最小，就是使均方误差最小化，这个方法叫做最小二乘法。

损失函数公式：

因为h(x)＝w1x1+w2x2+w3x3+…+wnxn+b

推理出

通过分析净水器滤芯剩余可用时间问题，确定问题的损失函数或效用函数，通过最优化损失函数或者效用函数，获得机器学习的模型，这是参数学习算法的一般套路。求损失函数可转化为典型的最小二乘法或者梯度下级问题最小二乘法的思想就是要使得真实值与预测值间的距离的平方达到最小。即真实值与预测值越贴合就证明预测的准确。

那么用数学公式表达出来就是：

线性回归算法思想简单且蕴含机器学习中的重要思想，实现容易。建模迅速，对于小数据量、简单的关系很有效，是许多强大的非线性模型的基础。其模型十分容易理解，结果具有很好的可解释性，有利于决策分析。

在本专利净水器滤芯更换时间预测的问题上，采用线性回归算法，通过累计流量、水温、多个水质指标等组成的训练集训练出的模型，预测出当前用户所使用的末端净水器需要更换滤芯的天数。

所述的骤5中，利用步骤4生成的深度学习模型，使用包含环境的用户数据进行预测，预测出净水器剩余可用时间。

请参见图3，在所述的步骤6中，以上述模型为依据，计算出净水器滤芯剩余的可用时间并显示在手机app上。

所述的步骤7中，用户在下一使用周期中，对所述净水器运行参数进行调整产生新的净水器参数，所产生新的净水器参数作为新的历史数据加入上述预定时间段的历史数据中。

本发明的基于深度学习的线性回归算法的个性化净水器智能学习方法由于采用了上述方案，使之与现有技术相比，具有以下的优点和积极的技术效果：

(1)本发明的基于线性回归算法的家用净水器可预测更换时间的方法通过人工智能深度学习获取的数据能及时判断水质的好坏，一旦水质变差，会及时提醒用户更换滤芯或耗材，避免已经失去功效的滤芯或耗材继续使用造成的二次生活用水污染；

(2)本发明的基于线性回归算法的家用净水器可预测更换时间的方法为用户提供安全可靠的净水饮用水，保证了用户家用水质的安全。

(3)本发明的基于线性回归算法的家用净水器可预测更换时间的方法通过建立一个不同水源、不同处理过程或过滤级别、不同的水温下的模型，用于精确提醒用户及时更换滤芯，保证用水健康。

以上对本发明的具体实施例进行了详细描述，但本发明不限制于以上描述的具体实施例，其只是作为范例。对于本领域技术人员而言，任何对于该系统进行的等同修改和替代也都在本发明的范畴之中。因此，在不脱离本发明的精神和范围下所做出的均等变换和修改，都应涵盖在本发明的范围内。