一种延性材料单轴本构关系测试方法与流程

本发明涉及材料力学性能测试，具体涉及一种延性材料单轴本构关系测试方法。

背景技术：

延性材料单轴本构关系(即拉伸应力-应变关系)是采用连续介质力学方法进行结构分析并实现工程设计的基础物理关系，也是联系材料与力学的重要“纽带”，对工程构件的设计和安全评价起着关键作用；在传统的拉伸试验中，试样等直段的真实横截面积和标距在拉伸试验过程中不断发生变化，在试样出现颈缩后，颈缩位置的材料不再处于平面变形，标距段工程应力-应变曲线表现出工程应力随测试应变增长而大幅下降的趋势；事实上，虽然试样颈缩后响应载荷会发生下降，但材料在颈缩过程中却仍在不断硬化，真实的应力则不断增大，试样颈缩区横截面中心点已处于三轴应力状态；因此，依靠传统的等直试样测量方法无法真实获得材料颈缩后的应力-应变关系。

技术实现要素：

本发明提供一种简单的、能够获得真实材料颈缩后的应力-应变关系测试方法。

本发明采用的技术方案是：一种延性材料单轴本构关系测试方法，包括以下步骤：

获取材料试样的连续载荷P和位移V的关系，所述试样为长方形中心具有圆孔的板状结构，P-V曲线满足下述关系

式中：R试样圆孔半径，S为弹性刚度，P*为特征载荷，m为位移指数，V_y为试样屈服位移；

根据S、P*和m获取材料的本构关系参数，包括弹性模量E、名义屈服应力σ_y和应变硬化指数n，通过有限元模拟得到临界断裂应力σ_f和临界断裂应变ε_f，即可确定材料的单轴本构关系；

其中S、P*和m满足下述关系：

式中：v^*为特征能量密度，A*为特征面积，W为试样的宽度，T为试样的厚度，k₁～k₅为无量纲常数；

其中：v^*、A*满足下述关系：

v^*＝Eⁿσ_y^1-n/(1+n)

A*＝(2W-πR)T

E、σ_y、n满足下述关系：

式中：σ为真应力，ε为真应变，K为应变硬化系数，且满足K＝Eⁿσ_y^1-n。

进一步的，所述试样中心圆孔半径R和试样宽度W的比值满足0.2≤R/W≤0.4。

进一步的，所述连续载荷P和位移V的关系通过试样的准静态拉伸试验获取。

进一步的，所述S、P*和m由试验获取的数据回归得到。

进一步的，所述参数k₁-k₅通过有限元分析实现标定。

本发明的有益效果是：

(1)本发明相对于传统的等直试样，方法简便易行，所得本构关系范围更为广泛；

(2)本发明采用中心具有圆孔的板状试样，在拉伸试验过程中，圆孔边缘中心点材料单元因三轴度不变而处于单轴应力状态，相对于等直试样，可避免颈缩对试验结果的严重影响。

附图说明

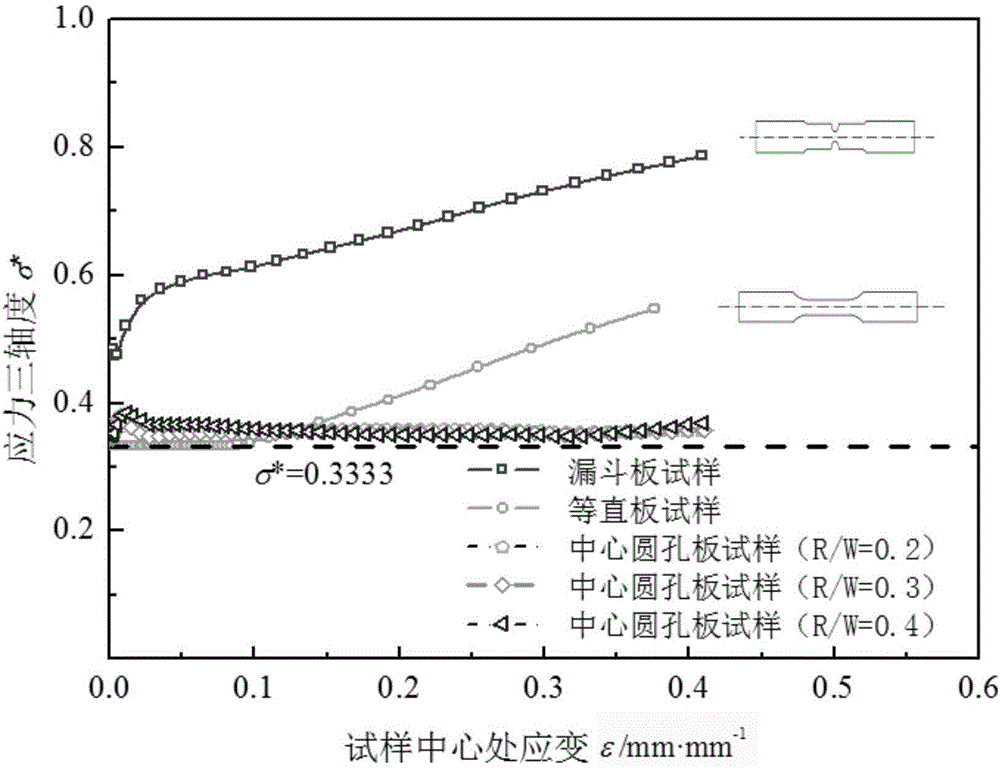
图1为试样在拉伸试验过程中的约束度变化曲线图。

图2为钛合金TA17中心圆孔板试样拉伸试验和本发明所得P-V曲线。

图3为本发明所得钛合金TA17的大变形单轴本构关系曲线图。

图4为本发明中试样结构示意图。

具体实施方式

下面结合附图和具体实施例对本发明做进一步说明。

一种延性材料单轴本构关系测试方法，包括以下步骤：

通过准静态拉伸试验，获取材料试样的连续载荷P和位移V的关系，所述试样为中心圆孔板试样，P-V曲线满足下述关系：

式中：R试样圆孔半径，S为弹性刚度，P*为特征载荷，m为位移指数，V_y为试样屈服位移；

根据S、P*和m获取材料的本构关系参数，包括弹性模量E、名义屈服应力σ_y和应变硬化指数n，通过有限元模拟得到临界断裂应力σ_f和临界断裂应变ε_f，即可确定材料的单轴本构关系；

其中S、P*和m满足下述关系：

式中：v^*为特征能量密度，A*为特征面积，W为试样的宽度，T为试样的厚度，k₁～k₅为无量纲常数；

其中：v^*、A*满足下述关系：

v^*＝Eⁿσ_y^1-n/(1+n)

A*＝(2W-πR)T

E、σ_y、n满足下述关系：

式中：：σ为真应力，ε为真应变，K为应变硬化系数，且满足K＝Eⁿσ_y^1-n，将材料的本构参数代入上式即可得到本材料的本构关系曲线。

试样中心圆孔半径R和试样宽度W的比值满足0.2≤R/W≤0.4；所述S、P*和m由试验获取的数据回归得到。

本发明采用的技术方案包括两部分，试样拉伸试验和试样的能量原理模型。

(1)中心圆孔板试样拉伸试验

由中心圆孔板试样拉伸试验获取准确的P-V曲线是本发明技术方案的首要条件；中心圆孔板试样的结构具有特殊性，即在拉伸试验过程中，圆孔边缘中心点材料单元因三轴度不变而处于单轴应力状态，即使在断裂前出现轻微的颈缩现象，但影响远小于等直试样，故采用该试样进行试验所得结果可以描述材料单轴应力状态下的大变形本构关系。

(2)能量原理模型

由理论和有限元分析可知，通过中心圆孔板试样拉伸试验所获取的P-V曲线包含了大量材料信息，通过P-V曲线确定弹性刚度S、特征载荷P*和位移指数m，代入下式：

即可获取被测材料的本构关系参数：弹性模量E，名义屈服应力σ_y和应变硬化指数n；如图1所示，中心圆孔板试样的圆孔边缘中心点材料单元在颈缩行为发生前处于单轴应力状态；根据拉伸试验所得的连续P-V曲线，标定得到弹性刚度S、特征载荷P*以及位移指数m，代入上式即可获得出材料的本构参数：名义屈服应力σ_y和应变硬化指数n，再通过有限元模拟得到临界断裂应力σ_f和临界断裂应变ε_f，进而确定材料大变形单轴本构关系。

下面通过具体实施例对本发明进一步说明：

对钛合金TA17中心圆孔板试样进行准静态拉伸试验并获取其大变形单轴本构关系曲线，其中试样宽度W为20mm，厚度T为3mm，中心圆孔半径R为7.5mm，即R/W＝0.375；试验设备为美国MTS 810 25KN电液伺服材料试验机、TestStraⅡ系统、TestWare/SX应用软件，采用632.12c-21(标距为25mm，轴向测量范围-10％～50％)应变引伸计测量室温下试样标距段的变形；轴向载荷由MTS810试验机测得。

数据处理过程：首先将试验所得P-V曲线进行零点修正，然后确定弹性刚度S、特征载荷P*和位移指数m，带入进行联立方程求解，即可获得材料的本构参数E、σ_y和n，再带入)即可得到材料的本构关系曲线；图2中将本发明所得P-V曲线与试验所得P-V曲线进行对比，两者十分接近；图3为本发明获取的钛合金TA17大变形单轴应力-应变曲线，从图中可以看出，通过本发明方案获取的大变形单轴应力-应变关系不仅包含了等直试样拉伸试验方法在试样颈缩以后不能获取的真实应力、应变，且相对于现有技术方案，本方案所得结果范围更为广泛，可行性更高，同时所得结果与现有技术方案具有良好的一致性，即现有技术方案进一步论证了本发明方案的有效性。

在实际应用中，依据情况，本发明使用范围可作适当修正拓宽；例如，对于不同厚度甚至满足平面应变条件的中心圆孔板试样模型，本发明同样适用，只需将参数k₁-k₅重新通过有限元分析实现标定，然后得到弹性刚度S、特征载荷P*和位移指数m，从而获取本构关系参数E、σ_y、n，再通过有限元模拟得到临界断裂应力σ_f和临界断裂应变ε_f，即可确定材料的大变形单轴本构关系。

表1为R/W数值不同时，通过有限元分析标定的参数k₁-k₅；

表1

蔡力勋、姚迪等人针对漏斗圆棒试样的拉伸试验通过迭代求解的有限元辅助分析方法，可以获得延性材料大变形真实应力-应变关系曲线；此方案为图3中的方案[1]；相对于传统的等直试样，其所获单轴应力-应变关系范围已大幅度增加；但在约束度的影响下，漏斗圆棒试样破坏时所得破断应变远小于本发明方案所得破断应变。

本发明适用于等向强化且本构关系符合幂律的延性材料；中心圆孔板试样的结构具有特殊性，即在拉伸试验过程中，试样的圆孔边缘中心点材料单元在颈缩发生前处于单轴应力状态，相对于等直试样，本发明更易于实行，所获得的单轴应力-应变关系范围更广，对工程结构设计和安全评估工作具有重要的意义。

参考文献

[1]蔡力勋，姚迪，包陈.材料拉伸真实本构曲线测试技术:中国，201210518207[P].2013-6-26.