一种非理想条件下高斯滤波替代框架组合导航方法与流程

本发明涉及一种非理想条件下高斯滤波替代框架组合导航方法，属于航天导航系统领域。

背景技术：

导航是引导飞行器、船舶或汽车等沿一定航线从一点运动到另一点的方法，其在军用领域和民用领域都有着广泛的应用。现代导航系统种类繁多，例如全球定位系统(GPS)、天文导航(CNS)、多普勒测速系统(Doppler)、惯性导航系统(INS)等[1]。由于GPS和INS两者之间具有较强的非相似性和互补性，将它们组合起来，便可以取长补短充分发挥各自的优势，同时克服GPS易受地形地物遮挡而导致定位中断和INS定位误差随时间而累计的缺陷。在GPS/INS组合导航系统中，由于系统本身元器件的不稳定性以及外部应用环境不确定因素的影响，导致系统噪声有时具有相关特性，比如当系统的输入源与传感器的输出且传感器测量值具有随机特性时，系统的过程噪声和量测噪声协方差将不为零。对于采用伪距的表达方式的紧耦合模型，并且由于实际应用中通信带宽的限制，使得组合导航系统可能同时具有非线性、时滞和噪声相关的特性，因此，设计更一般的算法是十分有必要。

下面简要介绍上述三类问题解决方案的发展现状并由此引出本文的算法。

针对常见的非线性系统，如制导或导航系统[2,3]，目标跟踪系统[1]等，在贝叶斯框架下依据概率密度非线性滤波算法可以分为两类。一类是高斯滤波算法[8]，如EKF[5]是以非线性函数的一阶泰勒展开形式来近似函数本身，对于强非线性函数近似能力较差，且存在计算Jacobi矩阵的问题，计算量大，不适合实时计算；UKF[6]算法是利用无迹变换来逼近状态后验概率密度函数，由于利用了样本点，因此不再需要计算Jacobi矩阵，但是在参数选择不当的时候容易造成状态误差协方差负定；Nrgaard M等提出的DDF算法[9]以斯特林多项式插值的方式去近似非线性函数，避免了陷入局部线性化的问题；CKF[7]算法是利用球径容积法则来实现对状态后验概率密度函数的近似，相比于UKF算法，减少了一个样本点但是数值稳定性却有了很大的提高。另一类是非高斯滤波算法，例如PF，但是计算量很大，不适合实时计算。

针对噪声相关问题，例如迎风航天器模型的过程噪声和量测噪声[10]，部分学者提出了解相关框架[11]，他们在状态方程中加入前一时刻的量测方程，将新构造出伪状态方程作为新系统的状态方程，通过选取合理的增益系数，达到新系统过程噪声和量测噪声解耦的目的，从而利用标准KF框架进行求解；另一部分学者采用两步预测代替一步预测的方式[12]，从而使得噪声之间相关性不再存在达到解决问题的目的；后来，经学者Guobin Chang指出这两种方法是等价的[13]。文章[14]通过将噪声看做是状态增量联和状态一起进行估计，给出了一种新颖的解决噪声相关问题的方法，并从理论上证明了其与前两种方法的等价性，仿真说明了此方法对解决线性系统且噪声相关问题的有效性。

针对量测量不能即时获取以及过程噪声和量测噪声相关的情况，研究主要从两方面展开，一类是确定性时滞，一类是随机时滞。针对确定性时滞问题目前主要的解决方法有重计算法、Alexander法和状态增量法等[15]；对于随机时滞问题，一般以满足Bernoulli分布的随机序列来构造新的量测数据，Hermoso-Corazo A等[16]针对一步随机时滞和两步随机时滞状态估计问题，给出了其在EFK算法和UKF算法框架下的处理方法。Wang X等[17]利用对状态后验概率密度估计的两步预测思想，融合状态增量的方法，解决了带有随机时滞和相关噪声的状态估计问题。

虽然针对这些非理想情况已有丰硕的研究成果，但是对于多种非理想条件共存的系统研究成果甚少，或者给出的算法形式不够简洁或统一，因此需要一种新的方法，从设计算法的角度，在新的框架下给出此类问题的解决方案。

技术实现要素：

本发明的目的是为了解决现有技术的替代框架下的高斯滤波算法将噪声和状态分开处理，导致估计精度不高，并且不具有一般性的缺点，而提出一种非理想条件下高斯滤波替代框架组合导航方法，所述方法基于非线性离散系统模型，并且满足如下条件：

k+1时刻的状态关于前k步量测值的一步后验概率密度函数是高斯的；

k+1时刻的实际量测值关于前k步量测值的一步后验预测概率密度函数是高斯的；

其特征在于，所述方法包括如下步骤：

步骤一：根据飞行器内的传感器测量值，获取飞行器在k时刻的状态值x_k；

步骤二：建立状态在k+1时刻的预测均值和协方差表达式：

其中，为k时刻对k+1时刻的预测估计值；是k+1时刻的n维状态向量的协方差矩阵；Q_k+1为k+1时刻的过程噪声ω_k+1的协方差矩阵；R_k+1为k+1时刻的量测噪声ν_k+1的协方差矩阵；S_k+1为k+1时刻的过程噪声和量测噪声的协方差矩阵，且S_k+1≠0；

步骤三：建立状态在k+1时刻的后验均值和协方差表达式：

其中，为增广后的状态向量的新息，其中为k+1时刻的新息n_k+1与k+1时刻的预测均值的互协方差；

步骤四：基于CKF滤波算法对步骤二和步骤三得到的表达式进行求解，得到修正后的均值和方差。

步骤五：根据所述修正后的均值和方差修正航向，实现导航。

本发明的有益效果为：本发明不同于以往噪声和状态分开处理的情况，本发明将过程噪声和量测噪声一起做为状态的一个扩张量进行滤波更新，将已知的噪声信息作为先验信息，在状态和量测的更新方程中用更新后的噪声的后验估计代替先验信息；通过仿真证明了其估计精度优于现有的滤波算法。同时，本发明提出的算法更具有一般性，选取合适的参数可以看出，一般高斯滤波算法是其在噪声不相关或不存在随机时滞情况的特例。

附图说明

图1为本发明的非理想条件下高斯滤波替代框架组合导航方法的流程图；

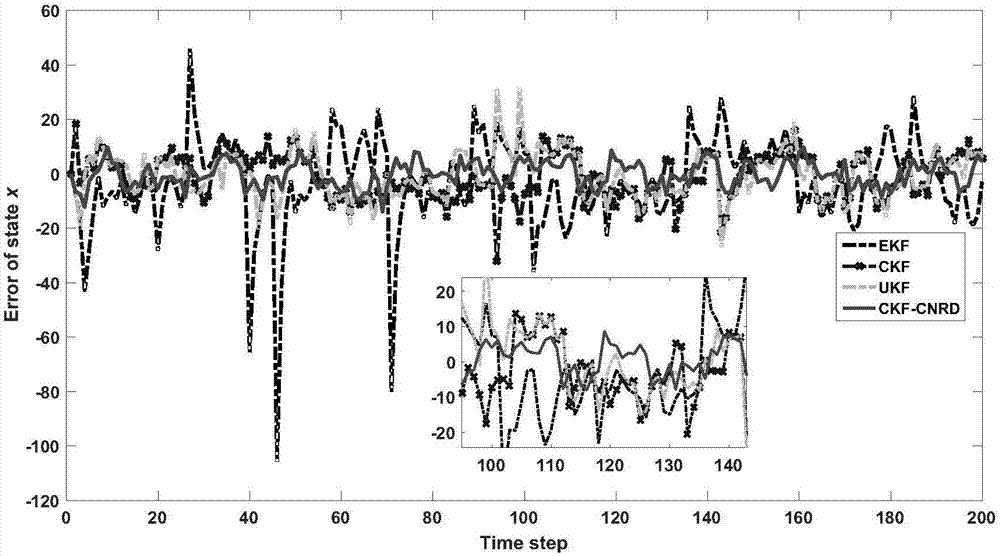
图2为EKF、CKF、UKF和CKF-CNRD的状态估计误差对比图；横坐标为时间，纵坐标为状态估计误差；

图3为EKF、CKF、UKF and CKF-CNRD的状态估计均方差对比图；横坐标为时间，纵坐标为状态估计均方差；

图4为CKF-CNRD的噪声估计均值效果图；横坐标为时间，纵坐标为噪声估计均值；

图5为CKF-CNRD噪声估计均方差效果图；横坐标为时间，纵坐标为噪声估计均方差；

图6为INS位置误差及KF算法、CKF-cnrd算法滤波误差对比图；

图7为INS速度误差及KF算法，CKF-cnrd算法滤波误差对比图；

图8为组合导航系统KF算法、CKF-cnrd算法位置误差对比图；

图9为组合导航系统KF算法、CKF-cnrd算法速度误差对比图。

具体实施方式

具体实施方式一：本实施方式的非理想条件下高斯滤波替代框架组合导航方法，是基于非线性离散系统模型的，非线性离散系统模型的表达式如下：

x_k＝f(x_k-1)+ω_k-1 (1)

z_k＝h(x_k)+ν_k (2)

这里x_k和z_k分别为k时刻的n维状态和m维观测向量，f(·)和h(·)分别为非线性函数，过程噪声ω_k-1和量测噪声ν_k分别为k-1时刻和k时刻的满足高斯分布的白噪声，其协方差阵满足

这里δ_kl为Kronecker delta函数；S_k≠0是过程噪声和量测噪声的协方差矩阵，并且这里假设初始状态x₀是高斯的，其均值为并且是独立于ω_k和ν_k。

假设实际量测值z_k在k＝1时的值总是可以获得的。然而，正如前面所讨论的，传感器的测量可能是随机延迟的。换句话说，实际测量输出y_k可能是当前输出z_k或者前面任意一个时刻的值，基于合理的假设，针对一步随机时滞的情况，我们以满足Bernoulli分布的随机序列来构造随机时滞量测数据，实际量测函数可以被表示为

这里，{γ_k；k＞1}表示一个独立的Bernoulli随机变量序列，取值为

p(γ_k＝1)＝E[γ_k]＝p_k (5)

我们的目标是对系统(1)、(2)、(4)在公式(3)、(5)及前面讨论的基础上设计替代框架算法，也就在最小均方误差意义下，利用前k时刻已知的量，通过计算状态的前两阶矩，得到一步预测和滤波估计后的状态值，即

注2.1:上标″∧″和″～″分别表示估计值及真值与估计值的差，″k+1|k″及″k+1|k+1″分别表示由k时刻预测k+1时刻及由k+1时刻修正k+1时刻，文章后面的部分均采用此定义，不再说明。

注2.2:由于本文考虑一步随机时滞的情况，预测值和修正值均是基于实际量测值Y_k的，这里Y_k＝{y₁,y₂,…,y_k}，而并非理论量测值z_k，不再赘述。

基于文章[18]，我们给出如下两个假设条件，这也是为了实现本发明需要的必要条件：假设2.1.状态x_k+1关于条件Y_k的一步后验概率密度函数是高斯的，即

假设2.2.关于实际测量值y_k+1在前k步测量值Y_k已知的条件下的一步后验预测概率密度函数依旧是高斯的，即

实际量测值的一步预测均值和协方差分别为

上述两个假设条件可以总结为：k+1时刻的状态关于前k步量测值的一步后验概率密度函数是高斯的；k+1时刻的实际量测值关于前k步量测值的一步后验预测概率密度函数是高斯的。

基于上面的假设，再将带有一步随机测量时滞和相关噪声的非线性系统替代框架，即：

将方程(2)代入(4)得到

将方程(1)和(11)代入公式(6)和(10)中一步预测均值的定义可得

显然，这里存在和即过程噪声和量测噪声相对于实际量测值的期望，由于Y_k中含有噪声项υ_k且本文中过程噪声和量测噪声相关，即Y_k与噪声ω_k及υ_k相关，故其期望均不为0，因此在一步随机量测时滞存在的情况下，不能利用传统的计算方法来直接得到状态和量测一步预测的估计值。本文采用替代框架的处理思想，将ω_k的均值0和协方差Q_k以及υ_k的均值0和协方差R_k看做ω_k和υ_k的一个先验信息，然后通过实际观测值y_k进行更新，我们假设更新后的均值和方差分别为及在滤波递推过程中，我们利用噪声的后验值而不是先验值进行计算。为了使得证明看起来更清晰，我们将证明过程中用到的前后估计的量都列写出来，以便形成一个完整的闭环。下面我们给出具体的计算步骤，分为两步来完成，即状态预测和状态修正。

本发明的方法包括如下步骤：

步骤一：根据飞行器内的传感器测量值，获取飞行器在k时刻的状态值x_k；

步骤二(即状态预测)：建立状态在k+1时刻的预测均值和协方差表达式：

这里

其中，为k时刻对k+1时刻的预测估计值；是k+1时刻的n维状态向量的协方差矩阵；Q_k+1为k+1时刻的过程噪声ω_k+1的协方差矩阵；R_k+1为k+1时刻的量测噪声ν_k+1的协方差矩阵；S_k+1为k+1时刻的过程噪声和量测噪声的协方差矩阵，且S_k+1≠0。

步骤三(即状态修正)：建立状态在k+1时刻的后验均值和协方差表达式：

其中，为增广后的状态向量的新息，其中为k+1时刻的新息n_k+1与k+1时刻的预测均值的互协方差。

步骤四：基于CKF滤波算法对步骤二和步骤三得到的表达式进行求解，得到修正后的均值和方差。

步骤五：根据所述修正后的均值和方差修正航向，实现导航。

具体实施方式二：本实施方式与具体实施方式一不同的是：

步骤二中建立状态在k+1时刻的预测均值和协方差表达式的具体过程为：

令带有噪声的增广状态向量为

则k+1时刻状态变量x的一步预测均值和协方差阵分别为

由于ω_k与x_k中所含的噪声ω_k-1不相关，故代入式(20)可得

这里和均为已知信息，通过简单的数学推导,可以得到一步预测均值和方差

由于ω_k+1和υ_k+1均与Y_k不相关，显然有

p(ω_k+1|Y_k)＝p(ω_k+1)＝N(ω_k+1；0,Q_k+1) (24)

p(υ_k+1|Y_k)＝p(υ_k+1)＝N(υ_k+1；0,R_k+1) (25)

故由公式(11)、(24)、(25)，根据高斯分布的计算规则[14]，在Y_k已知的条件下，其与y_k+1联和后验概率密度函数也是高斯的，即

由贝叶斯规则可知

重新整理公式(26)，可以得到

这里

进一步，p(l_k+1|Y_k+1)也是高斯的，可以依据公式(30)进行更新。

结合本文的假设及文献[18]，联和噪声的后验概率密度函数也是高斯的，满足：

以上即完成了对步骤二中公式(14)和(15)的证明。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是：

步骤三中，建立状态在k+1时刻的后验均值和协方差表达式的具体过程为：

考虑非线性系统(1)和(2)，并且假设k时刻的一步预测值已由步骤二给出，则k+1时刻的后验均值和协方差由下式给出：

这里定义如下：

同步骤二中的讨论，可得

这里和分别由公式(43)和(44)给定。

关于公式(43)和(44)中的各个变量的定义，由前面的定义，实际观测的一步预测均值为

由新息的定义及实际观测值y_k+1和其一步预测均值可得

状态和量测的一步预测协方差为

其中

其它步骤及参数与具体实施方式一或二相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是：

步骤四中，为了便于求解(例如使用matlab进行求解)，还需要一些步骤将步骤二和步骤三中的公式转化为可求解的形式，具体过程为：

①一步预测：

假设k+1时刻之前的所有信息已知，我们可以依据下列的数值格式进行迭代：

1)矩阵分解

2)容积点计算

这里ξ_i为容积点.

3)容积点传播

X_i,k+1|k＝f(X_i,k|k),i＝1,2,…,2n (47)

一步预测均值和协方差

②量测更新：

1)矩阵分解

2)容积点计算

这里n′＝2n+m，和分别表示状态，过程噪声和量测噪声分量。3)容积点传播

θ_i,k+1|k＝h(X_i,k+1|k),i＝1,2,…,2n (54)

可得

将式(56)-(60)代入(30)-(32),将所得公式代入修正表示式中，可以得到修正后的均值和方差。

具体实施方式五：本实施方式与具体实施方式一至四之一不同的是：

在步骤四执行完毕后，还包括数值仿真步骤，包括：

步骤A1：建立单变量非静态增长模型(UNGM)，来测试本发明的有效性，表达式为：

y_k＝(1-γ_k)z_k+γ_kz_k-1

其中ω_k和υ_k的协方差分别为Q_k＝10和R_k＝3，并且互协方差为S_k＝1。

步骤A2：对于所述单变量非静态增长模型，执行100次独立的蒙特卡罗仿真以计算均方根误差RMSE；其中，k时刻的均方根误差RMSE为：

和分别表示k时刻蒙特卡罗执行的真值和估计值。

步骤A3：根据步骤A2的计算结果得到统计结果。

图2和3表示EKF、CKF、UKF and CKF-CNRD之间的对比。一方面，因为EKF利用了一阶泰勒展开，其处理强非线性问题的能力很差，因此，我们可以看到EKF的估计值相当的差，相比来说，CKF和UKF的结果要更好一些。另一方面，由于测量值是随机延迟的，而EKF、CKF和UKF不具有处理延迟的能力，因此仿真中出现了许多尖点。从仿真图我们可以看到我们提出的CKF-CNRD算法完美解决了这两个问题。图4和5展示了ω_k和υ_k的最小均方误差估计。我们可以看到噪声的均值不再为0，因为8％的过程噪声超出了范围[-2,2]并且8.5％的量测噪声超出了范围[-0.8,0.8]，这意味着我们做这样的一个噪声估计是很有必要的。从仿真中可以看出，噪声估计值的尖点出现的时刻总是相同的，这与推导过程中的表达式是相符的，因为噪声的估计值总是相差一个倍数。

其它步骤及参数与具体实施方式一至四之一相同。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。

具体实施方式六：本实施方式与具体实施方式一至五之一不同的是：

在步骤四执行完毕后，还可以执行应用仿真步骤，具体如下：

利用伪距、伪距率的紧耦合表达方式对GPS/INS组合系统进行仿真，其中系统状态方程和量测方程如文献[19]所示，状态方程中的系数矩阵如文献[20]所示，系统方程中噪声矩阵惯导部分由陀螺仪马氏过程，陀螺仪白噪声和加速度计马氏过程组成，取值分别为(0.04/(57*3600))^2,(0.01/(57*3600))^2,(1e-3)^2，假设系统是一步随机时滞的，时滞概率取为0.3，利用Kalman滤波及本文提出的算法分别进行500s仿真，得到惯导系统及组合导航系统的位置误差和速度误差分别如图6至图9所示：

从仿真图6、7可以看出，单独的惯性导航系统存在一个误差越来越大的趋势，两种滤波算法均可减小误差且可得到较为精确的系统状态估计值。从图8、9可以看出，本文所提出的算法在KF算法性能较差的时候依然能够得到较为精确的目标位置和速度，反映出了本文提出算法在系统存在时滞情况的有效性。

综上，针对GPS/INS组合导航系统可能存在噪声相关和随机量测时滞的情况，本发明提出一种替代框架下的高斯滤波算法，不同于以往噪声和状态分开处理的情况，本发明将过程噪声和量测噪声一起作为状态的一个扩张量进行滤波更新，将已知的噪声信息作为先验信息，在状态和量测的更新方程中用更新后的噪声的后验估计代替先验信息，仿真证明了其估计精度优于现有的滤波算法。同时，本发明提出的方法更具有一般性，选取合适的参数可以看出，一般高斯滤波算法是其在噪声不相关或不存在随机时滞情况的特例。

<参考文献>

[1]黄晓瑞,崔平远,崔祜涛,GPS/INS组合导航系统自适应滤波算法与仿真研究，飞行力学19(2),2001,6,69-77.

[2]Seong Yun Cho,Byung Doo Kim,Adaptive IIR/FIR fusion filter and its application to the INS/GPS integrated system,Automatica 44(8)(2008)2040–2047.

[3]A.Noureldin,A.El-Shafie,M.Bayoumi,GPS/INS integration utilizing dynamic neural networks for vehicular navigation,Inf.Fusion 12(1)(2011)48–57.

[4]C.G.Park,S.Y.Cho,Y.Jin,H.W.Park,G.I.Jee,J.G.Lee,Analysis of measurement delay in INS/GPS integration with Kalman filtering,in:Proceedings of the 3rd ASCC,Shanghai,China,Jul.4–7,2000.

[5]Yaakov B S,Li X,Thiagalingam K.Estimation with Applications to Tracking and Navigation[M].New York:John Wiley and Sons,2001.

[6]Julier S J,Uhlmann J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE.2004,92(3):401-422.

[7]Arasaratnam I,Haykin S.Cubature Kalman Filters[J].IEEE Transactions on Automatic Control.2009,54(6):1254-1269.

[8]Ito,K.,Xiong,K.:‘Gaussian filters for nonlinear filtering problems’,IEEE Trans.Autom.Control,2000,45,(5),pp.910–927

[9]Nrgaard M,Poulsen N K,Ravn O.New Developments in State Estimation for Nonlinear Systems[J].Automatica.2000,36(11):1627-1638.

[10]Simon,D.:‘Optimal state estimation:Kalman,H∞,and nonlinear approaches’(Wiley-Interscience,2006)

[11]Feng,X.,Ge,Q.,Wen,C.:‘An optimal sequential filter for the linear system with correlated noises’.Control and Decision Conf.,CCDC’09,2009

[12]Wang,X.,Liang,Y.,Pan,Q.,&Yang,F.(2012).A Gaussian approximation recursive filter for nonlinear systems with correlated noises.Automatica,48,2290–2297.

[13]Chang,G.:‘Comment on“a Gaussian Approximation Recursive Filter for Nonlinear Systems with Correlated Noises”’,Automatica,2014,50,(2),pp.655–656

[14]Chang,G.:‘Alternative formulation of the Kalman filter for correlated process and observation noise’,IET Sci.Meas.Technol.,2014,8,(5),pp.310–318

[15]Gopalakrishnan A,Kaisare N S,Narasimhan S.Incorporating Delayed and Infrequent Measurements in Extended Kalman Filter Based Nonlinear State Estimation[J].Journal of Process Control.2011,21(1):119-129.

[16]Hermoso-Carazo A,Linares-Perez J.Extended and Unscented Filtering Algorithms Using One-Step Randomly Delayed Observations[J].Applied Mathematics and Computation.2007,190(2):1375-1393.

[17]Wang X,Liang Y,Pan Q,et al.Design and Implementation of Gaussian Filter for Nonlinear System with Randomly Delayed Measurements and Correlated Noises[J].Applied Mathematics and Computation.2014,232:1011-1024.

[18]X.X.Wang,Y.Liang,Q.Pan,Zhao Chunhui,Gaussian filter for nonlinear systems with one-step randomly delayed measure-ments,Automatica 49(4)(2013)976–986.

[19]Wang W,Liu Z,Xie R.Quadratic extended Kalman filter approach for GPS/INS integration[J].Aerospace science and technology,2006,10(8):709-713.

[20]袁信,俞济祥,陈哲.导航系统[M].北京航空工业出版社，1992。