一种基于L

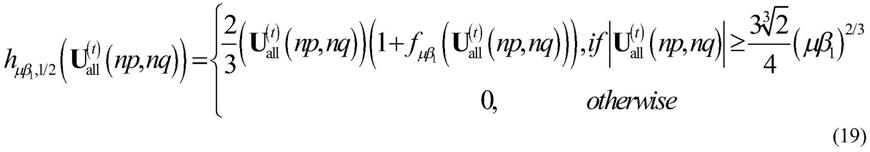
一种基于l
2,1/2
范数的无模糊稀疏sar成像方法
技术领域
1.本发明涉及一种基于l
2,1/2
范数的无模糊稀疏合成孔径雷达(synthetic aperture radar，简称sar)成像方法，属于稀疏信号处理和微波成像领域。


背景技术：

2.sar是现代高分辨率微波成像技术的一个主要研究方向。相比于传统光学成像，sar具有全天时、全天候的观测能力，因此被广泛应用于军事和民用领域。距离多普勒算法和chirp-scaling算法(简称csa)是常用的基于全采样数据的匹配滤波(matched filtering，简称mf)sar成像算法。然而，当采集到的数据是降采样时，mf算法恢复的图像具有严重的方位模糊，甚至导致重建失败。
3.稀疏sar成像技术是稀疏信号处理技术和sar成像的结合，通过解决lq(q＜0≤1)范数正则化问题可实现对观测区域的高分辨率稀疏重建。由于降采样信号不满足奈奎斯特采样定理，这使得传统mf算法不能用于场景恢复，而稀疏sar成像技术能够改善图像性能且能够基于降采样数据实现稀疏场景恢复。因此，为了解决数据降采样所引起的方位模糊问题，提出一种基于l
2,1/2
范数的无模糊稀疏合成孔径雷达成像方法。


技术实现要素：

4.本发明所要解决的技术问题是：提供一种基于l
2,1/2
范数的无模糊稀疏sar成像方法，基于稀疏信号处理技术开展降采样数据的处理工作，保证基于降采样数据的sar成像质量。
5.本发明为解决上述技术问题采用以下技术方案：
6.一种基于l
2,1/2
范数的无模糊稀疏sar成像方法，包括如下步骤：
7.步骤1，根据采集到的降采样数据，构建无模糊稀疏sar成像模型；
8.步骤2，基于无模糊稀疏sar成像模型，提出基于l
2,1/2
范数的正则化优化重构问题；
9.步骤3，通过阈值迭代恢复算法求解步骤2提出的基于l
2,1/2
范数的正则化优化重构问题，实现观测场景的稀疏重建。
10.本发明采用以上技术方案与现有技术相比，具有以下技术效果：
11.本发明基于降采样数据进行稀疏场景的精确重构，能够有效抑制方位模糊，获得高质量无模糊稀疏sar图像。
附图说明
12.图1是本发明一种基于l
2,1/2
范数的无模糊稀疏sar成像方法的实现流程图。
13.图2是本发明方法中的迭代恢复实现流程图。
14.图3(a)-图3(e)是本发明算法、l
2,1
范数、l1范数方法及csa对满采样和降采样仿真点目标的成像结果。其中，图3(a)是满采样时csa仿真结果；图3(b)是降采样时csa仿真结果；图3(c)是降采样时l1范数方法仿真结果；图3(d)是降采样时l
2,1
范数方法仿真结果；图3
(e)是降采样时本发明l
2,1/2
范数仿真结果。
具体实施方式
15.下面详细描述本发明的实施方式，所述实施方式的示例在附图中示出。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。
16.对于降采样数据，传统mf方法无法抑制方位模糊，会导致重建失败。因此本发明基于稀疏信号处理进行研究，以解决数据降采样所引起的方位模糊问题，并提出基于l
2,1/2
范数的无模糊稀疏sar成像方法，面向采集到的降采样数据，构建无模糊稀疏sar成像模型，提出基于l
2,1/2
范数的正则化优化重构问题，并通过阈值迭代恢复算法实现场景的高精度稀疏重建。
17.如图1所示，为本发明实施例基于l
2,1/2
范数的无模糊稀疏sar成像方法的实现流程图，具体实现步骤如下：
18.步骤s1：构建无模糊稀疏sar成像模型
19.令主多普勒频谱方位频率为f
η
，方位向周期采样导致的方位模糊区域的多普勒频率可以表示为：
20.fa＝f
η
+i
·
prf,i∈zandi≠0(1)
21.其中，prf是脉冲重复频率，i表示第i块方位模糊区域。
22.对于主多普勒区域，构建csa中的三个主要操作，即变标算子距离徙动校正及压缩算子和方位聚焦及相位校正算子和方位聚焦及相位校正算子和算子分别表示主多普勒区域和方位模糊区域的mf过程，和算子分别表示主多普勒区域和方位模糊区域的逆mf过程。fr和分别表示方位和距离向的傅里叶变换算子和逆傅里叶变换算子。基于所构建的算子，主多普勒区域mf过程和逆mf过程可以表示为：
[0023][0024][0025]
同理，利用方位模糊区域频率fa代替多普勒中心频率f
η
，即可得到方位模糊区域的csa算子及和相对应的mf过程及逆mf过程
[0026]
利用构建的算子可以表示基于近似观测的无模糊稀疏sar成像模型：
[0027][0028]
其中，y是二维降采样数据，ya是满采样数据，ξa和ξr分别表示方位向和距离向的降采样矩阵，n0是噪声矩阵，x和分别表示目标场景和方位模糊区域。
[0029]
步骤s2：基于l
2,1/2
范数的优化重构
[0030]
对于(4)中所构建的稀疏sar成像模型，可以通过解决如下的l
2,1/2
范数正则化问题来实现场景的重建：
[0031][0032]
其中，是重构的二维稀疏sar图像，β1是控制包含目标场景和方位模糊区域的总场景稀疏性的正则化参数，β2是控制目标场景稀疏性的正则化参数。x
all
表示包含了目标场景和方位模糊区域的总图像，表示为：
[0033][0034]
x
all
的范数可以表示为：
[0035][0036]
其中，x
np
和分别表示x和的第np行，np＝1,2,
…
,n
p
，n
p
是观测场景方位向总点数。
[0037]
步骤s3：迭代恢复
[0038]
针对(5)中的最优化问题，可以通过迭代恢复来实现观测场景的稀疏重建。阈值迭代算法输入采集的降采样回波数据y以及算子设稀疏重构的目标场景x
(0)
和方位模糊区域的初始化均为0，其对应的梯度值u
(0)
，和也均为0。迭代参数为μ，错误参数为ε，最大迭代步数为t
max
。当满足条件t≤t
max
且残差resi》ε时，如图2所示，执行下列步骤。
[0039]
步骤s31：估计残余数据值
[0040][0041]
步骤s32：更新梯度值
[0042][0043][0044]
其中，μ是控制算法收敛速度的参数，通常设置为常数。
[0045]
步骤s33：更新控制目标场景稀疏性的参数β2[0046][0047]
其中，|u
(t-1)
|
k+1
表示目标场景幅度值|u
(t-1)
|按降序排列的第k+1个最大分量。
[0048]
步骤s34：主成像区域的阈值收缩
[0049]
阈值算子为
[0050][0051][0052]
其中，阈值函数可以表示为
[0053][0054]
步骤s35：更新控制总场景稀疏性的参数β1[0055][0056]
其中，可以表示为
[0057][0058]
表示总场景幅度值按降序排列的第k+1个最大分量。
[0059]
步骤s36：总成像区域的阈值收缩
[0060][0061]
其中，阈值算子可以表示为
[0062][0063]
其中，阈值函数可以表示为
[0064][0065]
其中，
[0066][0067]
步骤s37：计算恢复图像的残差
[0068]
resi＝||x
(t)-x
(t-1)
||f(21)
[0069]
若满足条件t≤t
max
且resi》ε，则继续迭代，即t＝t+1，重复上述步骤。若不满足条件，则结束迭代，输出恢复的稀疏图像
[0070]
下面通过实验对本发明中提供的一种基于l
2,1/2
范数的无模糊稀疏sar成像方法进行验证。图3(a)-图3(e)均有五个仿真点，分别设为t1、t2、t3、t4和t5。其中，t1和t2之间、t2
和t3之间以及t3和t4之间的方位向间隔和距离向间隔均为100m，t4和t5之间的距离向间隔为100m，方位向间隔为10m。在该仿真中，采用满采样和降采样率为75％的数据。图3(a)为满采样时csa成像结果；图3(b)为降采样时csa成像结果；图3(c)为降采样时l1范数方法成像结果；图3(d)为降采样时l
2,1
范数方法成像结果；图3(e)为降采样时l
2,1/2
范数方法成像结果。可以看出，对于满采样数据，传统mf方法能够精确恢复，但不能区分方位向间隔较小的两个点目标，分辨率较低。对于降采样数据，传统mf方法无法抑制方位模糊和鬼影，也不能区分方位向间隔较小的两个点目标，导致重建失败。l1范数方法能够有效抑制鬼影，但由于靠近主瓣区域的鬼影和方位模糊能量较大，难以抑制。l
2,1
范数方法能够有效抑制方位模糊。而本发明所提出的l
2,1/2
范数算法不仅能抑制方位模糊，同时具有更高的分辨率，有效提高了成像性能。
[0071]
以上实施例仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明保护范围之内。