基于知识增强和重复学习的高效率自适应控制方法与流程

本发明涉及自适应控制领域，具体涉及一种基于知识增强和重复学习的高效率自适应控制方法。

背景技术：

迭代学习控制(ilc)(arimoto等人，1984)最初是从机器人领域提出的，因为工业机构通常用于执行重复性任务。在这种情况下，ilc方法可以根据先前操作的误差信息来改进控制性能，已经在广泛的实际应用中进行了探讨，例如在精确运动系统(tan等人，2001)、工业批量过程(lee和lee，2007)、高速交通控制(hou等人，2007；sun等人，2013)、列车轨迹跟踪(hou等人，2011)和不确定的机器人系统(tayebi，2004；choi和lee，2000)中均实现了较好的控制。

最初提出的ilc方法利用一类pid型算法(arimoto等人，1984；tan等人，2001；lee和lee，2007；hou等人，2007；sun等人，2013；hou等人)。pid-ilc方法可以直接应用于非线性不确定系统，因为它们需要很少的过程知识。在这个意义上，pid-ilc方法可以被称为“数据驱动控制”方法(hou和wang，2013)，由于难以在大规模和复杂的工业过程中获得精确的数学模型，这种方法已变得越来越具有吸引力(hou和wang，2013；hou和jin，2013；yin等，2014；xu等，2014)。

然而，典型的pid-ilc沿着迭代轴方向的系统瞬态性能通常较差，原因在于它没有完全使用可测量的状态和已知的过程信息。迄今为止所提出的ilc方案均要求在系统状态和相同的期望轨迹上具有相同的初始条件。否则，沿着迭代轴方向只实现有界收敛。

因此，如何利用已知的过程知识来提高系统的控制性能是当前的研究热点。最近，一些自适应ilc(ailc)方案(tayebi，2004；choi和lee，2000；frenchandrogers，2000；xu和wiswanathan，2000；qu和xu，2002；xu和xu，2004；rotariu，wang和chien，2013；yin等，2010)已经在ilc领域提出。针对控制对象是重复的线性时不变(lti)参数化系统，french和rogers(2000)首先将传统的参数适应规律引入到学习任务中，其中参数更新规律与连续时间自适应控制相同。唯一的区别是它通过使当前迭代的初始参数估计等于先前迭代的终端参数估计来在固定时间间隔上链接两个连续重复操作。

针对线性时变参数系统，有学者提出了基于复合能量函数(cef)的自适应ilc方法(xu和wiswanathan，2000；qu和xu，2002；xu和xu，2004；rotariuetal，2008；wangandchien，2013；yinetal2010)。因为未知的时变参数在可重复的控制环境下沿着迭代轴方向是不变的，因此时变参数沿着迭代轴(批到批)方向而不是时间轴方向更新。此外，当参数子集被称为时不变而其余是时变时，针对这种情况有学者也提出了具有混合参数更新定律的新的自适应ilc方法(xu和xu，2004)。混合参数更新法则分别包含用于时不变和时变参数的两个参数估计器。

注意，上述自适应ilc方法利用过程的已知知识，例如测量的系统状态、已知的系统结构、以及参数的已知的时变和/或时不变性质。它们能够确保沿着重复轴的跟踪误差的渐近收敛为零。同时，上述自适应ilc可以通过将目标轨迹的已知信息包括到控制律中来处理迭代变化的目标轨迹。因此，可以通过使用可用的过程知识来实现更期望的性能。然而，上述自适应ilc的开放性问题在于，为了保证收敛，需要所有迭代的初始系统状态相同。

与上述用于连续时间系统的自适应ilc方法相比，离散时间自适应ilc(dailc)方法(chi等人，2008)已经开始获得关注。几种dailc方法(chi等人，2008；chi等人，2007；li等人，2010；chi等人，2013)已经被提出用于时变参数系统。通过使用可测量的系统状态，已知模型结构和精确已知的参考轨迹，离散时间ailc方法渐近地实现理想的跟踪性能，而不需要在目标轨迹或相同的初始状态迭代上通过迭代的相同条件。然而，现有的离散时间ailc方法将所有未知的参数不确定性视为时变，即使参数不确定性是时不变的或者可以被精确地分离为时不变参数和时变参数，现有的离散时间ailc也将其视为时变参数，因此并未充分利用系统参数已知的有效信息(如全部时变，全部时不变，或部分时变部分时不变)，不能达到最好的控制效果。

技术实现要素：

本发明的目的是提出一种基于知识增强和重复学习的高效率自适应控制方法，该方法通过判断所研究对象的数学模型的系统参数的类型来建立自适应控制模式，能够增强对研究对象的控制性能。

为了实现上述目的，本发明专利采用如下技术方案，基于知识增强和重复学习的高效率自适应控制方法，包括以下步骤：

s1.建立实际电机系统的数学模型；

s2.判断所建立的数学模型的系统参数的类型；

s3.根据系统参数的类型对所研究的实际电机系统建立自适应控制模式；

s4.根据所建立的自适应控制模式对所研究的实际电机系统进行控制。

进一步地，在步骤s1中还包括如下步骤：如果所建立的数学模型是连续时间模型，需要将连续的时间模型进行离散化；如果所建立的数学模型如果是离散时间模型，则直接进行步骤s2。

进一步地，步骤s2中系统参数的类型包括时变系统参数模型、时不变系统参数模型和混合系统参数模型。

进一步地，步骤s3中对所研究的实际电机系统建立自适应控制过程时，先假设其通用数学模型为

其中xn(k)∈r和un(k)∈r分别表示实际电机系统的状态和输入；和表示已知的非线性函数；是未知的时变参数向量；是时不变的；m1、m2分别与实际电机系统的时变参数和常参数的数量相对应；b(k)是未知的时变输入增益；k∈{0,λ,t}，t是有限时间间隔的终点；n＝1,2,λ表示迭代次数；跟踪误差为en(k)＝xr,n(k)-xn(k)；

并且该数学模型满足以下假设：

(1)函数和满足线性增长条件，即，

其中，0<p1<∞，0<p2<∞；0<c1<∞，0<c1<∞。

(2)对所有k∈{0,λ,t}和迭代次数n，未知时变参数θ⁰(k)、目标轨迹xr,n(k)和初始状态值xn(0)均一致有界；

(3)对所有的k∈{0,1,λt}，b(k)是正的(或负的)、非奇异的和有界的，并且0＜bmin≤b(k)≤bmax，其中bmin和bmax分别是b(k)已知的上限和下限。

进一步地，对应步骤s2中的时变系统参数模型，通用数学模型简化为

xn(k+1)＝θ⁰(k)ξ⁰(xn(k))+b(k)un(k)

其中ξ⁰(xn(k))∈r^m表示已知的非线性函数；θ⁰(k)∈r^1×m是未知的时变参数向量；m表示实际电机系统的时变参数的数量。

则步骤s3中的自适应控制模式为：

其中，θ(k)＝[b^-1(k),b^-1(k)θ⁰(k)]，ξ(xn(k))＝[xr,n(k+1),-ξ⁰(xn(k))]^t，表示的θ(k)估计值且有界；c＞0，0＜|a|bmax＜2，a的符号与bmax的符号相同。

进一步地，对应步骤s2中的时不变系统参数模型，通用数学模型简化为

xn(k+1)＝θ⁰ξ⁰(xn(k))+bun(k)

其中θ⁰和b都是常数；

则步骤s3中的自适应控制模式为：

其中θ＝[b^-1,b^-1θ⁰],ξ(xn(k))＝[xr,n(k+1),-ξ⁰(xn(k))]^t，表示的θ估计值，并且是给定的且有界；c＞0，0＜abmax＜2，a的符号与bmax的符号相同。

根据权利要求4所述的基于知识增强和重复学习的高效率自适应控制方法，其特征在于，对应步骤s2中的混合参数模型，通用数学模型简化为

其中，存在两个非线性向量值函数和是时变的，是时不变的，输入增益b为常数；

则步骤s3中的自适应控制模式为：

其中，ξ2,n(k)＝[xr,n(k+1)-ξ2(xn(k))^t]^t，和分别用于估计θ1(k)和θ2；

对于时变θ1(k)，通过递归设计ide控制律，

对于时不变参数θ2，采用如下tde控制律

其中，q1和q2是正学习收益，q＝diag(q1,q2)、和的初始值和是给定且有界的。

本发明所提出的基于知识增强和重复学习的高效率自适应控制方法，通过判断所研究的实际电机系统的参数类型来建立自适应控制模式，所建立的控制模式不需要相同初始状态和相同参考轨迹的条件，并且能够充分利用测量的状态和已知的过程信息来增强对混合参数不确定性的实际电机系统的控制性能。

附图说明

图1是情形1的随机值m1(n)；

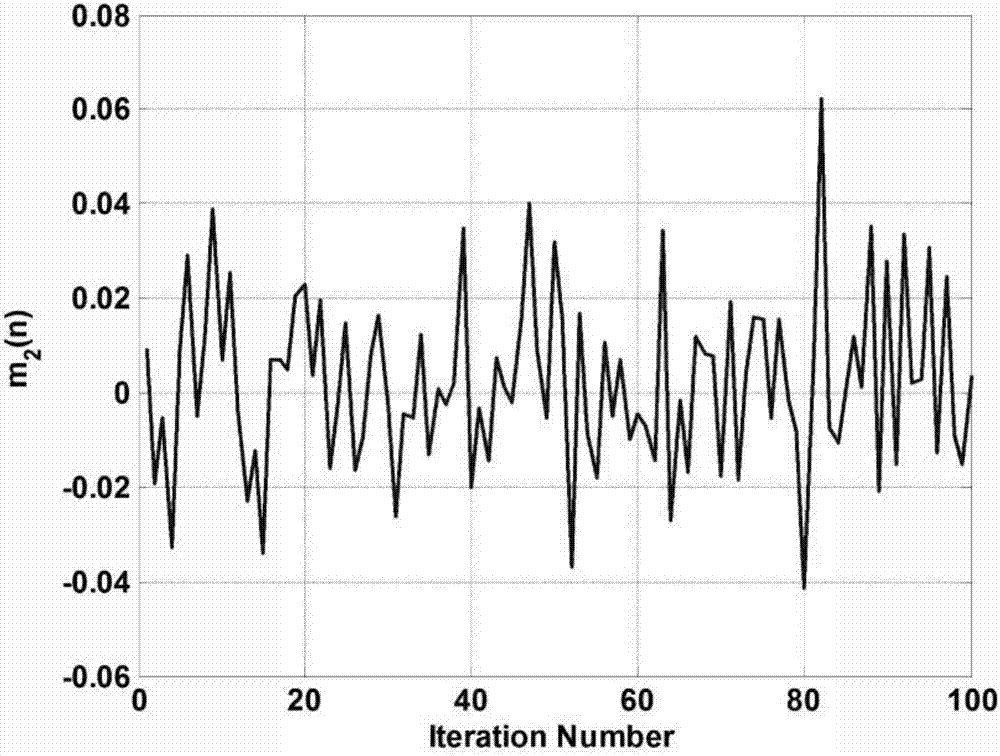
图2是情形1的随机值m2(n)；

图3是情形1的初始状态随机值；

图4是时不变参数不确定系统的跟踪误差；

图5是情形2的随机值m1(n)；

图6是情形2的随机值m2(n)；

图7是情形2中初始状态的随机值；

图8是时变参数不确定系统的跟踪误差；

图9是情形3的随机值m1(n)；

图10是情形3的随机值m2(n)；

图11是情形3中初始状态的随机值；

图12是混合参数不确定系统的跟踪误差。

具体实施方式

下面结合附图和实施例对本发明作进一步的说明。

基于知识增强和重复学习的高效率自适应控制方法，包括以下步骤：

s1.建立实际电机系统的数学模型；如果所建立的数学模型是连续时间模型，需要将连续的时间模型进行离散化；如果所建立的数学模型如果是离散时间模型，则直接进行步骤s2。

s2.判断所建立的数学模型的系统参数的类型；根据系统的参数类型可将系统分为时变系统参数模型、时不变系统参数模型和混合系统参数模型。

其中时变系统参数模型是指系统的参数的不确定性是随时间变化的；时不变系统参数模型是指系统的参数的不确定性是不随时间变化的；混合系统参数模型是指，系统的参数一组未知参数是不随时间变化的，其余的参数是随时间变化的。

s3.根据系统参数的类型对所研究的实际电机系统建立自适应控制模式。

s4.根据所建立的自适应控制模式对所研究的实际电机系统进行控制。

在本发明中，用于时变参数不确定系统的dailc方法，应用迭代差估计器来更新时变参数迭代，称为基于迭代差分估计的dailc方法(ide-dailc)。针对时不变参数不确定系统的dailc方法所提出的参数更新定律通过使用时间差估计算法沿着时间轴连续地估计参数，称为基于时间差估计器的dailc方法(tde-dailc)。用于混合参数不确定系统的所提出的dailc方法包括：时间差估计器，用于沿着时间轴连续地更新时不变参数；以及迭代差估计器，用于分别沿着迭代轴更新时变的参数。为简洁起见，将其表示为基于混合差分估计器的dailc方法(mde-ailc)。

假设研究对象的通用数学模型为：

其中xn(k)∈r和un(k)∈r分别表示实际电机系统的状态和输入；和表示已知的非线性函数；是未知的时变参数向量；是时不变的；m1、m2分别与实际电机系统的时变参数和常参数的数量相对应；b(k)是未知的时变输入增益；k∈{0,λ,t}，t是有限时间间隔的终点；n＝1,2,λ表示迭代次数；跟踪误差为en(k)＝xr,n(k)-xn(k)；

并且该数学模型满足以下假设：

(1)函数和满足线性增长条件，即，

其中，0<p1<∞，0<p2<∞；0<c1<∞，0<c2<∞。

(2)对所有k∈{0,λ,t}和迭代次数n，未知时变参数θ⁰(k)、目标轨迹xr,n(k)和初始状态值xn(0)均一致有界；

(3)对所有的k∈{0,1,λt}，b(k)是正的(或负的)、非奇异的和有界的，并且0＜bmin≤b(k)≤bmax，其中bmin和bmax分别是b(k)已知的上限和下限。

我们的控制目标是寻找一个合适的控制输入序列un(k)，k∈{0,λ,t-1}，使得实际电机系统输出xn(k)随着迭代次数的增加在整个间隔k∈{0,λ,t}上能够跟踪期望轨迹xr,n(k)。注意，假定系统输出xr,n(k)在迭代过程中是变化的。

定义en(k)＝xr,n(k)-xn(k)，可以将跟踪误差写为

en(k+1)＝xr,n(k+1)-θ⁰(k)ξ⁰(xn(k))-b(k)un(k)＝b(k)(b-¹(k)xr,n(k+1)-b-¹(k)θ⁰(k)ξ⁰(xn(k))-un(k))(3)

令θ(k)＝[b^-1(k),b^-1(k)θ⁰(k)]，ξ(xn(k))＝[xr,n(k+1),-ξ⁰(xn(k))]^t，可以将式(3)重新写为

en(k+1)＝b(k)(θ(k)ξ(xn(k))-un(k))(4)

针对时变系统参数模型：

通用数学模型简化为

xn(k+1)＝θ⁰(k)ξ⁰(xn(k))+b(k)un(k)

其中ξ⁰(xn(k))∈r^m表示已知的非线性函数；θ⁰(k)∈r^1×m是未知的时变参数向量；m表示实际电机系统的时变参数的数量。

则步骤s3中的自适应控制模式为：

其中，θ(k)＝[b^-1(k),b^-1(k)θ⁰(k)]，ξ(xn(k))＝[xr,n(k+1),-ξ⁰(xn(k))]^t，表示的θ(k)估计值且有界；c＞0，0＜|a|bmax＜2，a的符号与bmax的符号相同。

注1：注意，参数更新定律(6)是沿着迭代轴方向逐点进行的，并且未知的时变参数通过迭代更新进行迭代。

所提出的由式(5)-(6)给出的ide-dailc方法的收敛性如下所示。

定理1：对于满足假设1、2和3的系统(1)，由式(5)-(6)给出的ide-dilc方法保证①参数估计误差对于所有k∈{0,λ,t}和所有迭代是有界的和不增加的；②所有的跟踪误差，沿着迭代方向收敛。对系统(1)满足假设1、2和3，则控制律(5)及参数更新律(6)能够保证参数估计误差有界以及在整个有限区间k∈{0,λ,t}上非增，并且整个有限区间k∈{0,λ,t}的跟踪误差沿迭代轴渐近收敛。

针对时不变系统参数模型：

考虑离散时间定常系统，其在有限时间间隔内重复运行，则通用数学模型简化为

xn(k+1)＝θ⁰ξ⁰(xn(k))+bun(k),(7)

其中θ⁰和b都是常数。

令θ＝[b^-1,b^-1θ⁰],ξ(xn(k))＝[xr,n(k+1),-ξ⁰(xn(k))]^t。根据第2节中的步骤(4)，基于时间差估计器的离散时间自适应ilc方法(tde-dailc)可以被设计为：

其中表示的θ估计值，并且是给定的且有界；c＞0,0＜abmax＜2，a的符号与b的符号相同。

注2：与式(6)不同，提出的tde定律(9)沿时间轴方向更新，这与传统的离散时间自适应控制(goodwin和sin，1984)是相同的。然而，所提出的方法可以经由方程(10)链接两次连续的迭代以提高性能。

所提出的由式(8)-(10)给出的tde-dailc方法的收敛性如下。

定理2.考虑系统(7)满足假设4。应用由式(8)-(10)所给出的tde-dailc方法，可以保证①在固定时间间隔上的参数估计误差迭代地收敛到零；②所有连接的跟踪误差沿着迭代方向收敛为零。整个有限区间k∈{1,λ,t}的跟踪误差en(k)沿迭代轴渐近收敛。

针对混合系统参数模型：

通用数学模型简化为

其中，存在两个非线性向量值函数和是时变的，是时不变的，输入增益b为常数。

根据式(11)，误差方程为

其中，ξ2,n(k)＝[xr,n(k+1)-ξ2(xn(k))^t]^t。

学习控制律设计如下

其中，和分别用于估计θ1(k)和θ2。

由于和被称为系统(11)的时变和时不变不确定参数向量，式(11)的结构是先验已知的。因此，可以重写式(11)如下

其中，z1,n(k)和z2,n(k)是可测量的系统状态。

由于和是未知的参数向量，它们被估计的向量所代替，系统状态的估计值如下：

将状态估计误差定义为

对于时变θ1(k)，通过递归设计ide控制律，

对于时不变参数θ2，采用如下tde控制律

其中，q1和q2是正学习收益，q＝diag(q1,q2)、和的初始值和是给定且有界的。

因此，由式(13)和式(17)-(19)构造了一种用于混合参数系统(11)的新型made-dailc方法。

注3：注意，上述提出的控制律被简称为mde-dailc方法，因为其包含用于更新常数未知参数的时间差估计器(18)-(19)，以及迭代差估计器(17)变化的未知参数。因此，mde-dailc方法可以利用附加的过程信息来增强控制性能。

在进行收敛性分析之前，进行以下假设是为了进行严格的证明。

假设4函数和满足，

其中，0＜m1＜∞,0＜m2＜∞；0＜c1＜∞,0＜c2＜∞。

假设5未知参数和有界；参考轨迹和初始状态沿着迭代轴方向变化且有界；0＜bmin≤b(k)≤bmax，其中bmin和bmax分别是已知的上限和下限b(k)。

所提出的mde-dailc方法的收敛性如下所示。

定理3：对于满足假设5-6的系统(11)，由式(13)、(17)-(19)给出的ide-dilc方法保证①参数估计误差对于所有k∈{0,λ,t}和所有迭代是有界的和非增加的；②整个有限区间{1,λ,t}的跟踪误差en(k)沿迭代轴渐近收敛。

仿真研究：

考虑永磁直线电机如下(tan等人，1999)，

其中，v(t)是电动机速度(m/s)，m是移动的推力块(kg)，ffriction(t)是摩擦力(n)，fripple(t)是波动力(n)，fl是可测量的负载力(n)，沿着迭代轴进行模拟仿真，bv是粘性摩擦参数(n·s·m^-1)；fc是库仑摩擦的最小水平(n)，fs是静摩擦的水平(n)，vs是润滑油参数(m·s^-1)，x是电机位置，ar是表示振幅的常数fripple(t)。模拟时间t＝1s。永磁直线电机的参数认为是定值，如表i所示(tan等人，1999)。

表1.永磁直线电机的参数

在仿真中，线性电机(20)的重复连续时间模型离散化为

其中，h是采样周期，k表示采样时刻，n表示迭代次数；fl,n(k)被认为是系统的可测量扰动，其被假定为迭代变化。

目标轨迹表示为

vr,n(k)＝m1(n)sin(πk/1000),(22)

其中，m1(n)随n在间隔[0,0.01]中随机变化。因此，目标轨迹随着迭代而变化。

令，b＝h/m,则式(21)可改写成

根据式(1)-(4)的计算步骤，得到跟踪误差

en(k+1)＝vd,n(k+1)-vn(k+1)＝b(θξn(k)-un(k))(24)

其中，以及ide-dailc、tde-dailc和mde-dailc方法可以直接应用于线性电机系统(21)。

在仿真过程中，fl,n(k)＝m2(n)sin(πk/1000)和m2(n)沿着迭代轴方向随机变化。采样时间h＝0.001s，因此有限时间间隔的终端时刻为t＝1/h＝1000，即k∈{0,λ,1000}。

情形1.θ⁰和b都是常数。所有系统参数选择为常数，如表1所示。情形1的迭代随机变量m1(n)和m2(n)分别如图1和图2所示。初始状态vn(0)＝0.01×rand是随着迭代次数随机变化的，如图3所示。

通过选择a＝80，c＝0.1，应用由式(8)-(10)所给出的tde-ailc方法，得到最大跟踪误差如图3实线所示。显然，提出的tde-dailc方法对于时不变参数系统可取得满意效果。虽然初始系统状态和参考轨迹都通过迭代而改变随机改变的，但是跟踪误差的渐近收敛性是有保证的。

实际上，可以将定常参数向量视为时变的一种特殊情况。因此，以前提出的由式(5)-(6)所给出的ide-dailc方法也可以应用于情形i。为了比较，在相同的仿真条件下应用ide-dailc方法，a＝80，c＝0.1，对于有限区间内的所有离散时刻{0,λ,1000}，仿真结果如图4中的虚线所示。

可以看出，ide-dailc方法还可以实现时不变系统的渐近收敛。但是，参数估计值已经由时间差估计器在单次迭代内通过使用算法(9)更新(t-1)次。并且，迭代差估计器(6)每次迭代只更新一次。因此，对于时不变系统，tde-dailc方法实现了比ide-dailc更方法好的控制性能和更快的收敛。

情形2.θ⁰和b都是随时间变化的。时变因子被添加到如下所示的参数向量中，

其中，α(k)＝0.1sin(2πk/1000)。

对于这样的控制场景，池荣虎等(chi，hou，&sui，2007)提出ide-dailc方法，其随着迭代轴方向批量地估计时变参数，因为时变参数θ⁰(k)和b(k)相对于迭代是不变的。

在情形2的仿真研究中，m1(n)和m2(n)如图5和图6所示，它们都是迭代变化的。

情形2的迭代变化初始状态如图7所示。应用由式(5)-(6)所给出的ide-dailc方法，取a＝1000，c＝0.01，仿真结果如图8中的虚线所示。

如果时变参数被是定值，在相同的仿真条件下应用由式(8)-(10)所给出的tde-dailc方法，结果如图8中的红色实线所示。可以看出，ide-dailc方法很好地处理时变参数系统，并且能够在随机初始状态下渐进地跟踪迭代变化的目标轨迹。然而，由于使用时间差估计器，tde-dailc只能实现有界收敛，这仅对时不变不确定性有效。

情形3.假设参数θ⁰是定值，其余参数是随时间变化的，b是时不变的。也就是说，混合参数向量被假定为

注意，这种假设对于实际的线性电机应用是合理的，因为摩擦力通常随着电机速度而变化。而在实际的电机运行中，运动的推力块质量m、粘滞的摩擦参数bv和振幅ar通常是常数。

在情形3的仿真中，得到的m1(n)和m2(n)如图9和图10所示，并且图11中可以看出变化的初始状态。

选择q1＝100,q2＝10,将mde-dailc方法学习律(13)与参数估计算法(17)–(19)结合起来进行仿真研究，仿真结果如图12中的实线所示。

相比之下，对于这种控制场景，如果使用由式(8)-(10)所给出的tde-dailc方法将所有参数视为时间不变的，并使用由式(5)-(6)所给出的ide-dailc方法将参数视为时变参数，得到在相同仿真条件下的相应仿真结果如图12所示。

从图9-12可以看出，对于混合参数系统有如下结论，(a)所提出的mde-dailc方法在存在随机初始条件和迭代变量参考轨迹的情况下可以实现最佳收敛；(b)ide-dailc方法还通过将所有参数视为时变参数来实现渐近跟踪性能；然而其收敛速度慢于mde-dailc方法；(c)tde-dailc方法仅实现有界收敛。