一种固定时自适应神经网络无人机航迹角控制方法与流程

本发明涉及工业控制领域，特别涉及一种固定时自适应神经网络无人机航迹角控制方法。

背景技术：

无人机在许多方面展示出比传统飞机的优势，已经被用于执行许多复杂任务。自动飞行控制系统可以在无人机执行特殊任务时保证无人机性能。无人机执行任务的复杂性和特殊性对无人机控制时间、控制精度以及系统暂态和稳态性能提出了很高的要求。由于飞行环境的复杂多变，无人机系统是一个不确定的非线性系统，该系统具有非严格反馈结构，受到输入死区和输出限制的影响，这给设计控制器带来很大的困难。

由于神经网络具有很好的未知非线性函数逼近能力，神经网络控制是不确定非线性系统一种很好的控制方法。近些年来，在神经网络控制方面取得了很多研究成果。然而，这些研究成果仅针对带有严格反馈形式的非线性系统。非严格反馈系统是一种更为普遍的系统形式，严格反馈系统可以被认为是其特殊形式。由于非严格反馈系统中非线性函数包含整个状态变量，将既有的针对严格反馈系统设计的神经网络控制器用于控制非严格反馈系统会出现代数环问题。因此，需要将既有的神经网络控制方法扩展到非严格反馈非线性系统。

收敛速度是控制系统重要的性能指标，既有的神经网络控制方法仅能实现渐近稳定或有限时稳定。渐近稳定无法保证系统在有限时间实现稳定，无法用于对收敛时间要求严格的应用场合。有限时稳定的收敛时间取决于系统初值，然而，对于许多实际系统，其初始状态是难以获得的。此外，有限时稳定的收敛时间随初值的增长而无界增长，这限制了有限时稳定控制在初值非常大实际系统控制中的应用。为了克服上述不足，研究人员提出固定时稳定性。固定时稳定性的主要特征在于稳定时间边界是一个与初值无关的常数，这有助于收敛时间估计和控制器设计以满足收敛时间的要求。然而，目前还没有文献报道固定时自适应神经网络控制方法。

对于输入死区，既有文献采取神经网络和模糊逻辑估计和补偿死区非线性。然而，由于死区函数的非光滑特性，需要使用更多的节点、训练次数和模糊规则来逼近死区非线性，这增加了计算负担。自适应死区逆方法被用于解决死区问题。然而，未知死区参数的自适应律包含执行器输入u，而执行器输入u仅能在确定待估计的死区参数后才能获得，这使得该方法难以实际实施。另一种处理死区的方法是将死区建模为线性项和干扰项的组合形式，使用自适应方法或鲁棒方法来估计和补偿干扰。对于输出限制，既有文献采取凸优化方法，然而该方法依赖计算量大的算法。系统变换方法被证明能够很好的避免输出限制。最近，基于壁垒李雅普诺夫函数的设计方法被用于处理输出限制问题。然而，目前还没有文献报道带有死区和输出限制的系统固定时控制。

技术实现要素：

要解决的技术问题

为了避免现有技术的不足之处，本发明提出一种固定时自适应神经网络无人机航迹角控制方法，以满足无人机系统对跟踪时间、跟踪精度以及系统暂态和稳态跟踪性能的高要求，并考虑实际系统中普遍存在的控制死区和输出限制，使得无人机航迹角能够在固定时间内跟踪上理想轨迹。

技术方案

一种固定时自适应神经网络无人机航迹角控制方法，其特征在于步骤如下：

步骤1：建立无人机纵向系统航迹角动态数学模型：

式中，γ表示航迹角，α表示攻角，qb表示俯仰角速度，vt表示空速，ft表示发动机推力，δe表示升降舵偏角，m和iy表示质量和惯量，l(α,qb)和表示气动升力和俯仰力矩，且有如下表达式：

式中，s为参考翼面，ρ表示空气密度，表示平均弦长，cl和cm表示升力和俯仰力矩系数，可以写为：

其中，为由俯仰角速度对升力和俯仰力矩贡献的气动系数；为由攻角对升力和俯仰力矩贡献的气动系数；为由升降舵偏角对俯仰力矩贡献的气动系数；为零攻角和俯仰角速度下的升力系数；

将升降舵偏角δe＝u作为执行器输出，具有如下表达式：

式中，v表示待设计的执行器输入，mr和ml表示死区输入斜率，br和bl表示死区右断点和左断点；这里假设存在正常数使得

令x1＝γ，x2＝α，x3＝qb，则系统(1)可以表示为：

式中y为系统输出，g1(x1)＝1，由于实际系统中存在不确定参数，因此fi(x)和是未知函数，其中i＝1,2,3；这里假设的符号是已知的，如果的符号为正，可以找到常数使得如果的符号为负，可以找到常数使得假设非线性函数fi(x)满足lipschitz条件，即存在任意的实数x1,x2∈r^l使得|fi(x2)-fi(x1)|≤li||x2-x1||满足，其中li为lipschitz常数；

步骤2：确定理想输出值yd＝(10+2sin(0.5πt))°，输出限制为|y|≤kd，假设理想输出yd及其导数均有界，即可以找到正常数b0，b1使得|yd|≤b0，

步骤3：设计固定时自适应神经网络控制器、自适应参数更新律和固定时微分器，使系统输出能够在固定时间内跟踪上参考输出轨迹，同时保证所有状态变量有界，具体如下：

设计实际控制输入为：

式中

式中，χ3是正常数，辅助变量定义为：

式中λ3，θ3是正常数，r为隐层神经元数，m,n,p,q为满足m>n，p<q的正奇数，e3具有如下形式：

自适应参数的动态为：

λ3为正常数，ζ22为如下固定时微分器的状态：

式中μi＝iμ-(i-1)，μ∈(1,1+ι)，ι为充分小的正数，微分器增益l,m>0，k1，k2，σ1，σ2选择使得下述矩阵为hurwitz矩阵：

误差e3＝x3-α2，虚拟控制α2的表达式为：

式中，χ2为正常数，辅助变量定义为：

式中，kc＝kd-b0，λ2,θ2为正常数，e2为正常数，满足：

式中，ψ为正数，自适应参数的动态为：

式中，λ2为正常数，ζ21为如下固定时微分器的状态：

ζ11为固定时微分器；

误差e2＝x2-α1，虚拟控制α1定义为

式中，辅助变量定义为：

λ1和θ1为正常数，b1和e1定义为

式中ψ为正常数；

自适应参数的动态为：

式中，λ1为正常数；

步骤4：采用步骤3确定的控制参数对无人机实施控制，使航迹角能够在固定时间内跟踪上参考航迹角。

有益效果

本发明提出的一种固定时自适应神经网络无人机航迹角控制方法，相对于现有技术，本发明的创新性体现在以下四个方面：

(a)、本发明将固定时控制扩展到非严格反馈非线性系统。据我们所知，目前还没有文献报道针对非严格反馈非线性系统的固定时稳定控制方法。

(b)、本发明提出了简单有效的方法克服代数环问题。

(c)、本发明将反推设计，神经网络控制和固定时控制相结合，解决了复杂性爆炸问题，降低了自适应参数数目，实现了跟踪误差在固定时间内收敛到原点小邻域。

(d)、在固定时控制设计中考虑死区和输出限制，使得所设计的控制方案对于实际工程系统具有更为普遍的适用性。

本发明相对于现有技术，具有以下有益效果：

(a)、本发明所提出的固定时自适应神经网络控制方法，充分考虑了实际系统中存在的死区、系统不确定、输出限制等限制因素，适用于非严格反馈系统这样一种更为普遍的非线性系统，因而能够更好地应用于实际系统中。

(b)、所提出的控制方案降低了计算量，易于实施。使用固定时微分器估计虚拟控制的导数，避免了反推设计“计算复杂性爆炸”问题；与传统神经网络控制方法相比，所提出方法需要更新的自适应参数数量大为降低，而且自适应更新律设计也更为简单，这些都降低了控制算法的计算量；在实际控制器设计中，设计者无需在控制精度，计算负担和实时性能上折中，所提出的控制方案降低了对处理器计算性能的要求，因此降低了实施复杂性和困难性。

(c)、所提出的控制方案可以保证在固定时间内无人机航迹角跟踪上理想轨迹，适用于对收敛时间要求严格的任务场合。

附图说明

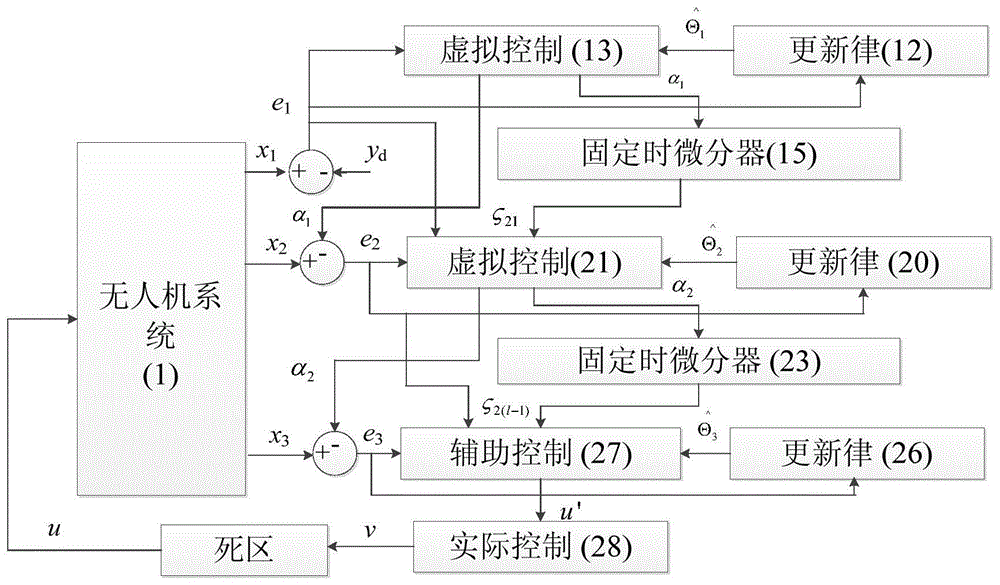
图1是本发明提供的一种固定时自适应神经网络控制方法的控制流程图

图2是本发明的实施例中航迹角及其参考轨迹的时间响应图

图3是本发明的实施例中攻角的时间响应图

图4是本发明的实施例中俯仰角速度的时间响应图

图5是本发明的实施例中死区控制输入时间曲线图

具体实施方式

现结合实施例、附图对本发明作进一步描述：

无人机在许多方面展示出比传统飞机的优势，已经被用于执行许多复杂任务。自动飞行控制系统可以在无人机执行特殊任务时保证无人机性能。无人机执行任务的复杂性和特殊性对无人机控制时间、控制精度以及系统暂态和稳态性能提出了很高的要求。由于飞行环境的复杂多变，无人机系统是一个不确定的非线性系统，该系统具有非严格反馈结构，受到输入死区和输出限制的影响，这给设计控制器带来很大的困难。

请参阅图1至图5所示，本发明提供一种固定时自适应神经网络控制方法，包括以下步骤：

步骤(1)中无人机纵向系统航迹角动态的数学模型为：

式中，γ表示航迹角，qb表示俯仰角速度，vt表示空速，ft表示发动机推力，δe表示升降舵偏角，m和iy表示质量和惯量，l(α,qb)和表示气动升力和俯仰力矩，且有如下表达式：

式中，s为参考翼面，ρ表示空气密度，表示平均弦长，cl和cm表示升力和俯仰力矩系数，可以写为：

其中，为由俯仰角速度对升力和俯仰力矩贡献的气动系数；为由攻角对升力和俯仰力矩贡献的气动系数；为由升降舵偏角对俯仰力矩贡献的气动系数；为零攻角和俯仰角速度下的升力系数。

升降舵偏角u＝δe常被当做执行器输出，具有如下表达式：

式中，v表示待设计的执行器输入，mr和ml表示死区输入斜率，br和bl表示死区右断点和左断点。

步骤(2)中参考输出为yd＝(10+2sin(0.5πt))°，输出限制为|y|≤kd。

步骤(3)设计固定时自适应神经网络控制律，实现控制目标。首先，将系统(1)写为控制系统的标准形式。令x1＝γ，x2＝α，x3＝qb，则系统(1)可以表示为：

式中y为系统输出，g1(x1)＝1，由于实际系统中存在不确定参数，因此fi(x)和(i＝1,2,3)是未知函数。

接下来，为控制系统(6)设计固定时自适应神经网络控制律。在控制器设计之前，对控制参数，控制增益和参考输出信号做如下假设：

假设1：死区(5)中的参数是未知的，但是其断点bl，br和斜率mr，ml是有界的，即存在正常数使得

假设2：的符号是已知的。如果的符号为正，可以找到常数使得如果的符号为负，可以找到常数使得

假设3：参考输出yd及其导数均有界,即可以找到正常数b0,b1使得|yd|≤b0，

假设4：非线性函数fi(x)满足lipschitz条件，即存在任意的实数x1,x2∈r^l使得|fi(x2)-fi(x1)|≤li||x2-x1||满足，其中li为lipschitz常数。

第一步：定义跟踪误差为e1＝x1-yd，其时间导数可以表示为：

径向基函数神经网络用于逼近未知非线性函数：

f1(x)＝w1^*ts1(x)+ε1(8)

式中w1^*,s1(x)和ε1分别表示径向基函数神经网络最优权值，高斯基函数和逼近误差。存在正常数使得

定义辅助变量：

式中λ1和θ1为正常数，r为隐层神经元数，m,n,p,q为满足m>n,p<q的奇数，b1和e1定义为：

式中ψ为正常数。

为自适应参数，其更新律为：

式中λ1为正数。

虚拟控制律可以设计为：

由于系统输出和参考输出受到限制|y|≤kd和|yd|≤b0,则有|e1|≤kc,式中kc+b0＝kd。

第二步：使用径向基函数神经网络逼近未知非线性函数f2(x),e2的时间导数为：

式中s2(x)和ε2分别表示径向基函数神经网络最优权值，高斯基函数和逼近误差，存在正常数使得

固定时微分器用于估计虚拟控制α1的导数：

式中ζ11,ζ21为固定时微分器状态变量，l,m>0,选择恰当的k1,k2,σ1,σ2使得(16)和(17)定义的矩阵是hurwitz矩阵，μi＝iμ-(i-1)且有μ∈(1,1+ι)，ι为充分小的正数，sig(·)^α＝|·|^αsign(·)。

设计辅助变量为：

式中λ2,θ2,χ2为正常数，e2具有如下形式：

为自适应参数，其自适应律为：

虚拟控制律设计为：

第三步：使用径向基函数神经网络逼近未知非线性函数f3(x)，则e3关于时间的导数可以表示为：

式中，w3^*,s3(x)和ε3为径向基神经网络最优权值，高斯径向基函数和逼近误差，可以找到正常数使得

固定时微分器用于获得虚拟控制α2的时间导数：

定义如下辅助变量：

式中λ3,θ3,χ3为正常数，e3具有如下的表达式：

为自适应参数，其更新律可以描述为：

辅助控制输入可以设计为：

执行器输入为：

进一步的，对控制系统进行稳定性分析，证明控制系统的固定时稳定性。首先，引入如下引理：

引理1:对于如下系统：

式中α>0,β>0,m,n,p,q为满足m>n,q>p的正常数。系统(29)将在以下式为上界的有限时间内到达原点：

引理2：对于z1∈r和χ1>0，则有：

引理3：对于任意c>0，a≥0，b>0，则有：

引理4：对于任意c>1，a≥0，b≤a，则有：

(a-b)^c≥b^c-a^c(33)

引理5：对于任意0<c≤1和xi≥0，则有：

引理6：对于任意c>1和xi≥0，则有：

引理7：对于微分器(15)，虚拟控制α1的时间导数可以在以下式为上界的有限时间内获得：

式中对称正定矩阵p1和q1满足：

矩阵a1如(16)式所示。

对称正定矩阵p和q满足：

pa+a^tp＝-q(38)

矩阵a如(17)式所示。

接下来，在第一步，考虑如下的李雅普诺夫函数：

式中

v1的时间导数为：

式中e2＝x2-α1。令则有：

式中

使用引理2，则有：

则，(40)变为：

使用引理3-4，可以得到：

类似的，可以得出：

将(45)和(46)代入(44)可以得到：

在第二步，构造如下李雅普诺夫函数：

式中

求取v2的导数：

令则有：

式中

使用引理2则有：

将(50)-(52)代入(49)则有：

当t≥td1，微分器可以给出虚拟控制导数的精确估计,即,则可以得到：

应用同第一步相似的方法，可以得到：

根据引理2可以得到：

将(55)-(57)代入(54)，可以得到：

第三步，控制输入误差可以表示为：

当由于u'的符号是由e3决定的，当e3>0，则有u'<0，并且当e3<0，则有u'>0。因此，我们有类似地，当我们也有

考虑如下的李雅普诺夫函数：

式中

v3的时间导数为：

令则有：

式中

使用引理2，则有：

将(62)-(64)代入(61)可得：

类似于第一步，我们有：

使用引理2，我们有：

当t≥td(l-1)时，微分器可以估计虚拟控制的导数，即将(66)-(68)代入(65)，(65)变为：

使用引理5-6，则有：

式中

由(70)，我们可以计算得到闭环系统最终边界：

在该边界外然而，难以给出方程(71)的解析解。闭环系统最终边界可以估计为：

v3的有界性意味着ei和的有界。由于θi是一个常数，我们有是有界的。由于e1和yd的有界，我们有系统输出y是有界的。考虑到e1,是有界的，χ1,λ1,θ1,r为常数，我们有和α1是有界的。由于e2和α1是有界的，我们有系统状态x2是有界的。由于和是连续函数具有有界定义域，我们有和ζ12是有界的。由(15)可知ζ11是有界的。由于ζ12,e1,e2，是有界的，且χ2，λ2，θ2，r为常数，则有和α2是有界的。由于e3和α2是有界的，则系统状态x3是有界的。类似的，可以证明xi,αi,ζ1i,ζ2i和v是有界的。因此，所有闭环信号是有界的。

假设系统输出y在时刻t＝t穿过输出限制，我们有李雅普诺夫函数v3将变为无穷，这与李雅普诺夫函数v3有界相悖，因此，系统输出将不会超过输出限制|y|≤kd。

我们可以找到一个常数使得则(70)变为：

令则(73)变为：

使用引理1，我们有v3将在以为上界的有限时间内收敛到区域

如果v3到达区域则有因此，跟踪误差将在以为上界的有限时间内到达紧致集合

(4)采用步骤(3)确定的控制律对无人机航迹角动态实施控制，使得无人机航迹角能够跟踪上理想的运动轨迹，并且保证系统输出不违反限制。

实施例：无人机航迹角动态

以无人机航迹角动态为例说明上述固定时自适应神经网络控制方法在实现无人机航迹角跟踪理想轨迹上的有效性。无人机航迹角动态可以表示为：

其中且有

系统参数选取为vt＝100m/s，ft＝8000n，m＝9295.44kg，s＝27.87m²，iy＝75673.6kg·m²，ρ＝1.7g/l，死区参数选为mr＝1，br＝0.6°，ml＝1.05，bl＝-0.8°。

本实施例的一种无人机航迹角动态固定时自适应神经网络控制方法，包括以下步骤：

(1)确定控制目标：参考输出信号选择为yd＝(10+2sin(0.5πt))°，输出限制为|y|≤22°。控制目标确定为系统输出可以在固定时间内跟踪上系统的参考输出，同时使得系统输出不超过限制。

(2)为实现控制目标，设计控制输入为：

式中u'具有如下的表述形式：

式中具有如下表述形式：

(3)根据李雅普诺夫函数稳定性分析，控制器和微分器参数选为λi＝θi＝10，r＝5，χi＝0.1，p＝5，q＝9,m＝9，n＝5，ψ＝0.05，λi＝5，k1＝5，k2＝10，σ1＝5，σ2＝10，l＝10，μ1＝1.2，μ2＝1.4，可以证明，这组控制参数满足李雅普诺夫稳定性。

(4)采用步骤(3)确定的控制参数对无人机航迹角动态实施控制，使得无人机航迹角能够跟踪上理想的运动轨迹，同时使得系统输出满足输出限制|y|≤22°。

所提供的一种固定时自适应神经网络控制方法的流程图示于图1。航迹角及其参考轨迹的时间响应示于图2。攻角的时间响应示于图3。俯仰角速度的时间响应示于图4。死区控制输入时间曲线示于图5。从这些图中可以看出，系统输出在固定时间内跟踪上参考轨迹，系统输出没有超过限制，其他状态变量和死区控制输入有界。