一种信息融合下的飞行器抗干扰控制方法与流程
本发明涉及一种飞行控制方法,特别是涉及一种信息融合下的飞行器抗干扰控制方法,属于信息融合控制方法领域。
背景技术:
飞行控制系统设计是保证飞机安全飞行的重要基础。反步法被广泛应用于飞控系统设计中,但是要求系统模型准确、外界环境无干扰,而且存在“复杂度爆炸”问题,为了解决这个问题,动态面设计以及指令滤波设计被应用于降低设计复杂度。目前,很多应用在飞控系统设计中的智能控制都是基于状态完全可测的,但在实际系统中,部分系统状态不易直接测量,或由于测量设备在经济上和使用性能上的限制,使得不可能获得系统的全部状态向量,从而影响飞行器的控制性能。
《hypersonicvehiclelongitudinalcontrolbasedonslidingmodeobserveranddynamicsurfacecontrol》(yuyanguo,shixingwang,binxu,etal,《ieeechinesecontrolconference》,2016年)采用滑模观测器来估计系统的迎角和航迹角,并基于反步法设计控制器,将滑模观测器得到的估计值作为控制器输入,该方法可以有效估计未知状态并实现跟踪控制。但是,当系统存在测量噪声以及模型不确定性和外界干扰时,噪声会导致系统状态估计不准确,而扰动会影响系统的控制性能,因而该方法可能达不到期望的控制效果。
技术实现要素:
要解决的技术问题
本发明的目的在于提供一种信息融合下的飞行器抗干扰控制方法,以解决飞行器部分状态不可测以及存在模型不确定性和外界干扰时的跟踪控制问题。
技术方案
一种信息融合下的飞行器抗干扰控制方法,其特征在于步骤如下:
步骤1:考虑含有未知时变干扰的飞行器纵向动力学模型为
其中,v、h、γ、α和q分别表示速度、高度、航迹角、迎角和俯仰角角速度;d、l和ma分别表示阻力、升力和俯仰力矩;m、iy和g分别表示飞行器质量、y轴的转动惯量和重力加速度;t表示推力;di,i=v,h,γ,α,q表示模型不确定性和外界扰动构成的集合干扰;
步骤2:选择x=[vhγαq]t为滤波状态量,根据动力学模型(1)-(5)建立系统状态方程
其中,噪声w(t)=[dv(t)dh(t)dγ(t)dα(t)dq(t)]t的统计特性是未知的;f(x,t)∈r5是根据(1)-(5)得到的非线性函数;
考虑状态α和γ不可测,引入惯导信息作为量测信息,建立量测方程
zins(t)=hx(t)+v(t)(7)其中,
状态方程(6)和观测方程(7)线性化离散化
其中,xk表示k时刻的状态;φk/k-1=i+f(tk-1)σt表示tk-1时刻至tk时刻的一步转移阵,其中σt为滤波采样时间,
根据离散型线性干扰方程(8)构建自适应kalman滤波器
其中,
定义
步骤3:定义xh=[x1x2x3x4]t,其中x1=h,x2=γ,x3=θ,x4=q,θ=α+γ;因为γ很小,取sinγ=γ;考虑到tsinα远小于l,在控制器设计过程中忽略;
根据动力学模型(2)-(5),高度子系统转换成以下严格反馈形式
根据动力学模型(1),速度子系统写成以下形式
其中,
步骤4:定义跟踪误差
其中,
设计一阶滤波器为
其中,τ2>0表示滤波器参数;
设计扰动观测器为
其中,
定义跟踪误差
其中,
设计一阶滤波器为
其中,τ3>0表示滤波器参数,由设计者给出;
其中,
定义跟踪误差
其中,
设计一阶滤波器为
其中,τ4>0表示滤波器参数,由设计者给出;
其中,
定义跟踪误差
其中,
其中,l4>0表示扰动观测器参数;
根据动力学模型(8),定义跟踪误差
其中,
设计扰动观测器为
其中,lv>0表示扰动观测器参数;
步骤5:根据得到控制信号u(t)和uv(t),返回到飞行器的动力学模型(1)-(5)中,对高度和速度进行跟踪控制。
步骤4中所述的vd=40m/s。
有益效果
本发明提出的一种信息融合下的飞行器抗干扰控制方法,该方法考虑飞行器部分状态不可测且存在未知系统噪声,通过设计自适应kalman滤波器融合飞控和惯导信息来实现状态估计;基于反步法框架,将自适应kalman滤波器得到的状态估计值用于设计控制器;利用扰动观测器来估计由飞行器模型不确定性和外界干扰形成的复合干扰;按照上述步骤得到飞行器的控制输入以实现高度和速度的跟踪控制。
与现有技术相比有益效果为:
(1)本发明考虑了飞行器存在模型不确定性和外界干扰,通过设计扰动观测器来实现对系统未知部分的估计,将飞行器控制器设计与惯导/飞控系统信息融合有机结合。
(2)本发明考虑了系统部分状态不可测,并通过设计自适应kalman滤波器融合惯导与飞控信息来实现状态估计,从而保证控制系统的控制性能。
(3)本发明考虑了系统噪声统计特性未知,并通过设计自适应kalman滤波器实现噪声统计特性的估计,并减小噪声对系统的影响。
附图说明
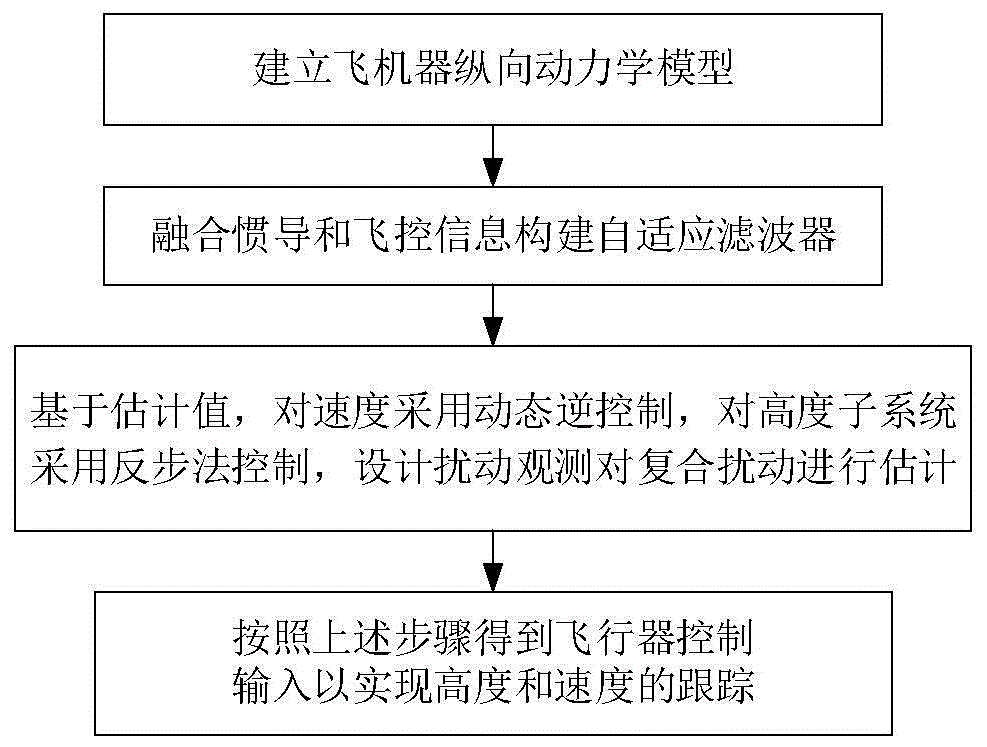
图1是本发明一种信息融合下的飞行器抗干扰控制方法流程图。
图2是本发明一种信息融合下的飞行器抗干扰控制方法原理图。
具体实施方式
现结合实施例、附图对本发明作进一步描述:
本发明的一种信息融合下的飞行器抗干扰控制方法流程图如图1所示,所发明内容用于改进飞行器存在未知时变扰动以及系统部分状态不可测时的跟踪控制问题,其具体实施步骤如下:
(a)考虑含有未知时变干扰的飞行器纵向动力学模型为
其中,v、h、γ、α和q分别表示速度、高度、航迹角、迎角和俯仰角角速率;d、l和ma分别表示阻力、升力和俯仰力矩;m、iy和g分别表示飞行器质量、y轴的转动惯量和重力加速度;t表示推力;di,i=v,h,γ,α,q表示模型不确定性和外界扰动构成的集合干扰;dh=5sin(2t),dγ=0.1sin(2t),dα=0.2cos(t),dq=0.2sin(t),dv=cos(2t);(1)中相关气动力和力矩的定义如下
其中,ρh表示空气密度;sw表示机翼面积;ca表示平均气动弦长;q表示动压;cl,cd和cm分别表示总的气动升力系数、阻力系数和俯仰力矩系数;cd0、cdα、
(b)根据图2,选择x=[vhγαq]t为滤波状态量,根据模型(1)-(5)建立系统状态方程
其中,w(t)=[dv(t)dh(t)dγ(t)dα(t)dq(t)]t;非线性函数f(x,t)为
考虑状态α和γ不可测,引入惯导信息作为量测信息,建立量测方程
zins(t)=hx(t)+v(t)(7)
其中,
状态方程(6)和观测方程(7)线性化离散化
其中,xk表示k时刻的状态;φk/k-1=i+f(tk-1)σt表示tk-1时刻至tk时刻的一步转移阵,其中σt为滤波采样时间,
根据离散型线性干扰方程(8)构建自适应kalman滤波器
其中,
(c)定义xh=[x1x2x3x4]t,其中x1=h,x2=γ,x3=θ,x4=q,θ=α+γ;因为γ很小,取sinγ=γ;考虑到tsinα远小于l,在控制器设计过程中忽略。
根据动力学模型(2)-(5),高度子系统转换成以下严格反馈形式
根据动力学模型(1),速度子系统写成以下形式
其中,
(d)定义跟踪误差
其中,
设计一阶滤波器为
其中,τ2>0表示滤波器参数,由设计者给出;
设计扰动观测器为
其中,
定义跟踪误差
其中,
设计一阶滤波器为
其中,τ3>0表示滤波器参数,由设计者给出;
设计扰动观测器为
其中,
定义跟踪误差
其中,
设计一阶滤波器为
其中,τ4>0表示滤波器参数,由设计者给出;
设计扰动观测器为
其中,
定义跟踪误差
其中,
设计扰动观测器为
其中,l4>0表示扰动观测器参数,由设计者给出。
根据动力学模型(8),定义跟踪误差
其中,
设计扰动观测器为
其中,lv>0表示扰动观测器参数,由设计者给出。
(e)根据得到的控制输入u和uv,返回到飞行器的动力学模型(1)-(5)中,对高度和速度进行跟踪控制。
- 还没有人留言评论。精彩留言会获得点赞!