一种两栖仿蟹多足机器人步行足抗饱和有限时间运动控制方法

本发明涉及多足机器人运动控制方法。属于控制技术领域。

背景技术：

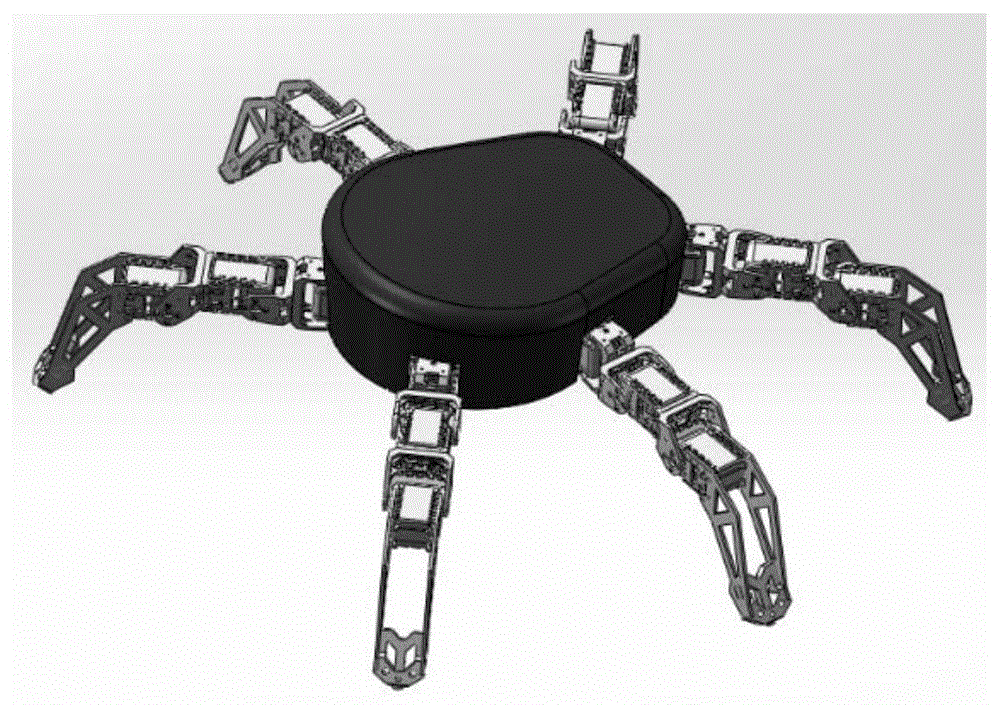
当今世界，科学技术迅猛发展，海洋资源开发需求日益扩大。针对近海海底、浅滩等复杂环境下海洋设施巡检、海洋资源勘探及数据采集、近海侦查、防御与救援等领域的诸多任务，需要研发一种两栖仿蟹多足机器人来完成以上作业任务需求。如图1所示。

两栖仿蟹多足机器人的设计研究交叉融合了多学科、多领域的技术，其爬行模式中的运动控制问题是两栖仿蟹多足机器人研究课题中的一项关键内容，同时也是机器人研究内容中的关键技术难点，其运动控制技术的可靠性决定了两栖仿蟹多足机器人的作业效率和智能化水平，也是保证机器人完成特定作业任务的重要前提。

两栖仿蟹多足机器人由于自身的多关节、非线性、多冗余度以及时变特性等特点，导致其运动学、动力学的运动模型具有高度不确定性。首先，机器人在运动过程中需要克服由于自身建模误差导致的模型不确定性以及在海底行走运动时海流的扰动等因素造成的影响；同时，实际控制过程中由于执行器系统非线性特性也会导致输入饱和问题，以上问题都对机器人步行足的控制精度以及响应速度提出了较高的要求。如何有效提高机器人步行足轨迹跟踪控制精度和速度，如何保证机器人在执行器饱和情况下实现稳定高精度快速控制，都是两栖仿蟹多足机器人运动控制研究中需要解决的关键性问题。

技术实现要素：

本发明是为了解决现有的仿蟹多足机器人的步行足轨迹跟踪控制存在精度差、速度慢的问题。

一种两栖仿蟹多足机器人步行足抗饱和有限时间运动控制方法，包括以下步骤：

s1、针对两栖仿蟹多足机器人建立机器人步行足动力学模型：

式中：为集总不确定性，θ∈r³、分别表示机器人步行足关节角度、关节角速度、关节角加速度矢量；其中m0(θ)、g0(θ)为模型已知标称部分，分别表示正定惯性矩阵、科氏力和离心力项、重力和浮力项产生的恢复力项，δm(θ)、δg(θ)对应为建模误差导致的不确定部分，fs(θ)为机器人受到的地面广义反力项，τd为海流扰动，τ为期望控制力/力矩输入，sat(·)为饱和函数；

s2、基于两栖仿蟹多足机器人步行足动力学模型，确定自适应有限时间干扰观测器：

滑动变量η∈r³为满足以下辅助动力学方程的变量；

式中：为d的估计值，为滑模项，为辅助动力学方程的增益；

定义为干扰估计误差，可得：

自适应有限时间干扰观测器如下：

式中：ξ为辅助变量，为α的估计值，为观测器增益；σ表示对时间t的积分变量；α集总不确定性d的导数边界值；

由式自适应有限时间干扰观测器和干扰误差可得：

自适应律为：

其中，γ、δ是正常数；

s3、利用辅助系统处理输入饱和的影响，辅助系统如下：

式中，ζ＝(ζ1,ζ2,ζ3)^t为辅助系统的状态向量，a＝diag{ai}3×3、b＝[b1,b2,b3]^t为参数矩阵及参数向量，其中ai＞0，bi＞0，i＝1,2,3；sgn(ζ)＝(sgn(ζ1),sgn(ζ2),sgn(ζ3))^t，sgn(·)为符号函数；p＝diag{||pi||}3×3，其中pi为控制增益矩阵m0^-1的第i行；

s4、利用基于输入饱和下基于自适应有限时间干扰观测器aftdo的快速终端滑模控制器对机器人步行足运动进行控制；

所述的基于输入饱和下基于自适应有限时间干扰观测器aftdo的快速终端滑模控制器如下：

τ＝τ0+τ1+τ2

τ2＝-m0(θ)(aζ+b+σ0psgn(ζ))

其中，τ0为等效控制项，τ1为干扰观测器的辅助控制项，τ2为饱和补偿项；e、分别为关节角位移跟踪误差和角速度跟踪误差；s为全局快速终端滑模面；λ＞0，μ＞0为正对角矩阵；p和q为奇数且p＜q；k1,k2＞0为控制参数。

进一步地，所述的关节角位移跟踪误差和角速度跟踪误差分别如下：

e＝θ-θd

其中，θd为机器人步行足关节期望角度。

进一步地，所述的全局快速终端滑模面为：

其中，(·)^p/q表示幂运算。

进一步地，辅助动力学方程的增益如下：

其中，c0、γ0、γ1、γ2、γ3、γ4均为正常数。

进一步地，所述观测器增益

进一步地，所述的机器人步行足动力学模型中的sat(τ)＝[sat(τ1),sat(τ2),sat(τ3)]^t，sat(·)为饱和函数：

其中，i＝1,2,3，τmax、τmin分别为最大控制力/力矩输入和最小控制力/力矩输入。

进一步地，所述针对两栖仿蟹多足机器人建立机器人步行足动力学模型的过程包括以下步骤：

首先构建机器人机械臂动力学模型：

式中，θ∈r³、分别表示机器人步行足关节角度、关节角速度、关节角加速度矢量；m(θ)＝m0(θ)+δm(θ)，g(θ)＝g0(θ)+δg(θ)；其中m0(θ)、g0(θ)为模型已知标称部分，δm(θ)、δg(θ)代表建模误差导致的不确定部分，fs(θ)为机器人受到的地面广义反力项，τd为海流扰动；

将集总不确定性引入机器人机械臂动力学模型，得到：

然后基于输入饱和确定机器人步行足动力学模型

有益效果：

本发明针对两栖仿蟹多足机器人步行足轨迹跟踪控制问题，综合考虑输入饱和情况下模型参数不确定性和海流扰动不确定性，提出了一种自适应有限时间干扰观测器(adaptivefinitetimedisturbanceobserver，aftdo)来解决海流干扰和建模误差产生的集总不确定性观测问题，并采用不依赖于精确动力学模型的控制方法，提出一种考虑输入饱和的基于自适应有限时间干扰观测器的全局快速终端滑模控制器，实现对两栖仿蟹多足机器人的步行足轨迹跟踪控制。

aftdo是将系统模型参数不确定性和海流扰动不确定性处理为集总不确定性，构造辅助动力学方程，设计自适应律，改进设计自适应有限时间干扰观测器，实现对集总不确定性的快速准确估计。

输入饱和下基于aftdo的全局快速终端滑模控制方法是在自适应有限时间干扰观测器的基础上，结合全局快速终端滑模控制快速且在有限时间内到达滑模面的优势，考虑输入饱和情况，构造输入饱和辅助系统，设计输入饱和下基于自适应有限时间干扰观测器的快速终端滑模控制器，提高机器人步行足轨迹跟踪控制精度和响应速度。

附图说明

图1为两栖仿蟹多足机器人示意图；

图2为两栖仿蟹多足机器人步行足模型；

图3为自适应有限时间干扰观测器性能曲线图，其中图3(a)为扰动d1估计性能，图3(b)为扰动d1估计误差；图3(c)为扰动d2估计性能，图3(d)为扰动d2估计误差；图3(e)为扰动d3估计性能，图3(f)为扰动d3估计误差；

图4机器人步行轨迹跟踪控制响应曲线，其中图4(a)为关节1轨迹跟踪性能，图4(b)为关节1轨迹跟踪误差；图4(c)为关节2轨迹跟踪性能，图4(d)为关节2轨迹跟踪误差；图4(e)为关节3轨迹跟踪性能，图4(f)为关节3轨迹跟踪误差。

具体实施方式

在说明具体实施方式之前，首先对本发明的参数定义进行一下说明：

m0(θ)——正定惯性矩阵；——科氏力和离心力项；g0(θ)——重力和浮力项产生的恢复力项；θ∈r³、——机器人步行足关节角度、关节角速度、关节角加速度矢量；e＝θ-θd——跟踪误差；τ——控制输入；τd——海流扰动；d——包括模型不确定性、地面广义力以及海流扰动的集总不确定性。

具体实施方式一：

本实施方式所述的一种两栖仿蟹多足机器人步行足抗饱和有限时间运动控制方法，包括以下步骤：

s1、基于两栖仿蟹多足机器人步行足动力学模型进行两栖仿蟹多足机器人步行足动力学模型变换：

两栖仿蟹多足机器人步行足运动模型如图2所示，对步行足建立坐标系，其中步行足的固定坐标系为o-x0y0z0，髋关节坐标系为o-x1y1z1，股关节坐标系为o-x2y2z2，胫关节坐标系为o-x3y3z3，步行足末端点坐标系为o-x4y4z4，其中步行足固定坐标系也是步行足与机器人机体连接处的坐标系。

两栖仿蟹多足机器人步行足动力学方程采用基于欧拉-拉格朗日方法推导的机器人机械臂动力学模型：

式中：θ∈r³、分别表示机器人步行足关节角度、关节角速度、关节角加速度矢量；m(θ)＝m0(θ)+δm(θ)，g(θ)＝g0(θ)+δg(θ)，fs(θ)＝ji^tfi。其中m0(θ)、g0(θ)为模型已知标称部分，δm(θ)、δg(θ)代表建模误差导致的不确定部分，fs(θ)为机器人受到的地面广义反力项，τd为海流扰动，ji^t为机器人第i条步行足的雅克比转置矩阵；fi＝[fix,fiy,fiz]^t为处于支撑相的第i条步行足受到的反力向量。

令为集总不确定性，代入式(1)得：

由于机器人步行足在摆动过程中不会受到地面力的作用，此外机器人在运动过程中由于建模误差会产生模型不确定性和海流扰动的影响，同时由于执行器系统存在输入饱和的非线性特性，将会导致系统控制器不能继续对系统误差信号产生响应，进一步使控制器不能正常发挥作用。所以本发明考虑机器人在海流干扰和建模误差产生的集总不确定性以及输入饱和的情况，建立机器人步行足动力学模型为：

式中：为集总不确定性，θ∈r³、分别表示机器人步行足关节角度、关节角速度、关节角加速度矢量；m(θ)＝m0(θ)+δm(θ)，g(θ)＝g0(θ)+δg(θ)，fs(θ)＝ji^tfi。其中m0(θ)、g0(θ)为模型已知标称部分，δm(θ)、δg(θ)代表建模误差导致的不确定部分，fs(θ)为机器人受到的地面广义反力项，τd为海流扰动，sat(τ)＝[sat(τ1),sat(τ2),sat(τ3)]^t，τ为设计的期望控制力/力矩输入，sat(·)为饱和函数：

s2、基于两栖仿蟹多足机器人步行足动力学模型，设计自适应有限时间干扰观测器：

定义滑动变量为并且η∈r³满足以下辅助动力学方程：

式中：为d的估计值，为滑模项，且标量为辅助动力学方程(5)的增益。

定义为干扰估计误差。则由式(2)和式(5)可得：

为了估计和补偿集总参数的不确定性，下面设计自适应有限时间干扰观测器：

式中：ξ为辅助变量，为α的估计值，为观测器增益。

由式(7)和干扰误差定义可得：

对于辅助动力学方程(5)和自适应有限时间观测器系统，选择下式为未知增益：

则自适应律设计为：

其中：γ，δ是正常数，则估计误差将在有限时间内收敛到包含平衡点在内的有界区域。

s3、设计输入饱和辅助系统：

系统(3)中考虑了系统输入饱和问题，对于实际控制系统，期望控制输入τ和实际控制输入sat(τ)之间的差值δτ要足够小，因为控制输入饱和时还要满足系统的能控性。由于扰动和系统状态有界，则所需的控制输入有界。为了满足这个假设，参数σ0可以较大。定义δτ并假设其满足条件：||δτ||＝||τ-sat(τ)||≤σ0，其中σ0为已知常数。

设计辅助系统来处理输入饱和的影响，设计辅助系统如下：

式中，ζ＝(ζ1,ζ2,ζ3)^t为辅助系统的状态量，a＝diag{ai}3×3和b＝[b1,b2,b3]^t为设计矩阵及设计向量，其中ai＞0，bi＞0，i＝1,2,3。此外，sgn(ζ)＝(sgn(ζ1),sgn(ζ2),sgn(ζ3))^t，sgn(·)为符号函数；p＝diag{||pi||}3×3，其中pi为控制增益矩阵m0^-1的第i行。辅助状态量在有限时间内收敛到零。

s4、基于机器人在海流干扰和建模误差产生的集总不确定性以及输入饱和的情况，设计输入饱和下基于自适应有限时间干扰观测器aftdo的快速终端滑模控制器为：

τ＝τ0+τ1+τ2(12)

τ2＝-m0(θ)(aζ+b+σ0psgn(ζ))(15)

其中τ0为等效控制项，τ1为干扰观测器的辅助控制项，τ2为饱和补偿项，k1,k2＞0为控制参数。

为了充分说明本发明创新性，现对本发明控制器的设计过程和原理进行如下说明：

p1：采用基于欧拉-拉格朗日方法推导的机器人机械臂动力学模型建立两栖仿蟹多足机器人步行足动力学方程：

式中：θ∈r³、分别表示机器人步行足关节角度、关节角速度、关节角加速度矢量；m(θ)＝m0(θ)+δm(θ)，g(θ)＝g0(θ)+δg(θ)，fs(θ)＝ji^tfi。其中m0(θ)、g0(θ)为模型已知标称部分，δm(θ)、δg(θ)代表建模误差导致的不确定部分，fs(θ)为机器人受到的地面广义反力项，τd为海流扰动，τ为控制输入。

令为包括模型不确定性、地面广义力以及海流扰动的集总不确定性，代入式(16)得：

其中：

ρ＝τd+fs(θ)(19)

上式具有以下性质：

性质1：矩阵为斜对称矩阵；

性质2：矩阵m0(θ)正定；

性质3：不等式||g0(θ)||≤g0成立，c0、g0为已知正常数。

引理1：系统模型不确定性未知但是满足以下有界条件：||δm(θ)||≤γ0、||δg(θ)||≤γ3；m^-1(θ)存在且有界，m^-1(θ)≤γ2。

假设1：ρ未知但有界，||ρ||≤γ4。

引理2：假设d的导数未知但有界，用未知常数α表示。

其中，γ0、γ1、γ2、γ3、γ4为已知正常数。

由以上性质、定理和假设可以得出：

其中：

引理3：考虑如下系统：f(0)＝0,x∈r,假设有李雅普诺夫函数v(x)，满足条件(1)v(x)为正定函数，(2)存在任意实数a>0，0＜b＜∞，以及原点的开放区域u0∈u，这样那么系统是有限时间稳定的，且有限收敛时间为

p2、自适应有限时间干扰观测器：

基于步行足动力学模型以上假设、性质条件，设计自适应有限时间干扰观测器，定义滑动变量为并且η∈r³满足以下辅助动力学方程：

式中：η为满足上述辅助方程的变量，为d的估计值，为滑模项，且标量为满足式(17)辅助动力学方程(22)的增益。

定义为干扰估计误差。则由式(17)和式(22)可得：

为了估计和补偿集总参数的不确定性，下面设计自适应有限时间干扰观测器：

式中：ξ为辅助变量，为α的估计值，为观测器增益。σ表示对时间的积分变量，表示在0到时间t的范围内对g0(θ)的积分；α集总不确定性d的导数边界值；

由式(24)和干扰误差定义可得：

对于辅助动力学方程(22)和自适应有限时间观测器系统，选择下式为未知增益：

则自适应律设计为：

其中：γ，δ是正常数，则估计误差将在有限时间内收敛到包含平衡点在内的有界区域。

证明如下：

第一步需要证明s＝0在有限时间内可达，将李雅普诺夫函数取为：

v1＝s^tm0(θ)s(28)

对上式关于时间求导得：

由性质1、3得：

由式(20)和(26)可得：

通过以上证明可以得出结论，滑动变量s可以在有限时间内收敛到零，其中v1(0)为v1的初始值，此后始终成立。基于等效变换，将等效为式(23)中的即

以上证明了在有限时间内到达s＝0的状态，接下来需要证明干扰误差有限时间稳定性，选取李雅普诺夫函数为：

定义根据式(25)，对v2关于时间求导：

将误差等效变换和自适应律(27)带入上式得：

由于下面不等式成立：

代入式(34)得：

由于：

则：

根据引理3李雅普诺夫有限时间稳定理论，干扰误差在有限时间内收敛到有界集合中，其中干扰误差的收敛时间为以上便完成了提出的自适应有限时间干扰观测器的稳定性证明。

p3、输入饱和下基于aftdo的全局快速终端滑模控制器设计：

考虑控制系统输入饱和，则式(17)可改写为：

假设2：定义δτ并假设其满足条件：||δτ||＝||τ-sat(τ)||≤σ0，其中σ0为已知常数。

首先设计一个辅助系统来处理假设2下输入饱和的影响，设计辅助系统如下：

定义此时关节角位移和角速度的跟踪误差为：

e＝θ-θd(41)

其中θ为机器人步行足关节实际角度；θd为机器人步行足关节期望角度。

采用的全局快速终端滑模面为：

其中(·)^p/q表示幂运算，其中λ＞0，μ＞0为设计的正对角矩阵，p和q为奇数且p＜q，使系统可以在有限时间内快速到达平衡点，并且在到达滑模面s＝0后，误差将在有限时间内收敛到平衡点e＝0，其收敛时间ts为：

对于定义的全局快速终端滑模面，当误差状态e远离平衡点时，线性项λe使系统快速趋向s＝0，当误差状态接近原点时，系统的收敛速度主要由非线性项μe^p/q实现，因此，系统状态可以迅速而精确的收敛到平衡点。

对定义的滑模面对时间求导得：

其中，

考虑设计辅助系统产生的信号，基于提出的自适应有限时间干扰观测器，根据干扰观测器式(24)、辅助系统式(40)、滑模面式(45)以及相关定理和假设，设计输入饱和下基于自适应有限时间干扰观测器的快速终端滑模控制器为：

τ＝τ0+τ1+τ2(46)

τ2＝-m0(θ)(aζ+b+σ0psgn(ζ))(49)

其中τ0为等效控制项，τ1为干扰观测器的辅助控制项，τ2为饱和补偿项。

引理4：给定以下一阶非线性不等式：其中v(x)表示关于状态x∈r，κ＞0，0＜η＜1的正李雅普诺夫函数，那么对于给定的任意初始条件v(x(0))＝v(0)，函数v(x)可以有限时间内收敛到原点，收敛时间为：

证明如下：

第一步先证明基于自适应有限时间干扰观测器的全局快速终端滑模控制器稳定。选择李雅普诺夫函数为：

将选取的李雅普诺夫函数对时间求导，并代入式(45)得：

将设计的控制律式(46)代入上式得：

其中，(||s^tsgn(s)||1)为1范数，与2范数(||s||)存在不等式关系，并且选取其中χ＞0为一个常数，为一个正常数使成立，得到：

根据引理4，系统能够在有限时间内收敛，收敛的有限时间为以上便完成了快速终端滑模控制器的有限时间稳定性证明。

然后证明考虑输入饱和后给出的辅助系统的有限时间收敛性。选择李雅普诺夫函数为：

根据式(40)，v4对时间的导数为：

根据引理4，设计的辅助系统(40)能在有限时间内收敛，且有限收敛时间为：

为了证明考虑输入饱和的基于自适应有限时间干扰观测器的全局快速终端滑模控制方法的有限时间收敛性能，即证明机器人控制器设计为式(47)-(49)时，包含观测器和输入饱和在内的整个系统的有限时间稳定性。

选择李雅普诺夫函数为：

对时间求导并根据式(38)、(53)、(55)可得：

其中

根据引理3，考虑输入饱和情况下基于自适应有限时间干扰观测器的全局快速终端滑模控制器能够在有限时间内收敛，收敛时间为以上便完成了整个系统的稳定性和有限时间收敛性能的证明。

实施例

为了验证以上关节控制器的控制性能，按照具体实施方式一的方案将对机器人步行足的动力学控制通过matlab进行仿真，验证进设计后的控制器(本发明)性能。自适应有限时间干扰观测器的参数分别为：c0＝50，θ0＝[60,100,120]^t，γ＝1，δ＝0.1；控制器的参数设置分别为：λ＝diag[5,5,5]，μ＝diag[0.1,0.1,0.1]，k1＝diag[5,5,5]，k2＝diag[0.01,0.01,0.01]，p＝3，q＝5；考虑输入饱和情况下设计的辅助系统参数为：a＝diag[5,3,5]，b＝[0.1,0.2,0.3]^t，p＝diag[0.01,0.01,0.02]，σ0＝100，设置输入饱和界限值为±50nm；模型参数不确定度为标称系统动力学参数的20％，定义集总不确定性为：d＝[1+0.3sin(0.3t)cos(0.2t),0.5+0.1sin(0.2t)cos(0.1t),0.1+0.1sin(0.2t)]。机器人步行足各关节的角度位置为[θ1,θ2,θ3]＝[30°,45°,90°]，步行足初始位置随机设定。对比分析改进观测器效果以及参考控制算法和改进提出的控制方法的控制性能。

改进观测器的观测效果以及观测误差仿真结果如下图3所示；图3为自适应有限时间干扰观测器性能曲线图，其中图3(a)为扰动d1估计性能，图3(b)为扰动d1估计误差；图3(c)为扰动d2估计性能，图3(d)为扰动d2估计误差；图3(e)为扰动d3估计性能，图3(f)为扰动d3估计误差。

由图3可知，参考观测器方法和改进的观测器方法均能较好的估计观测不确定扰动d，最后估计误差都能保持在零点附近振荡，且振荡范围很小；但是改进的观测器性能效果更优于参考观测器性能，改进观测器方法在估计速度和估计误差方面均比参考观测器方法效果更好，因此验证了改进自适应有限时间干扰观测器的有效性。

下面验证各关节按照期望轨迹运动时的跟踪控制性能。设置三个关节的位移曲线为正弦曲线，各关节的幅值大小不同，分别为θ1＝30sin(t)，θ2＝45sin(t)，θ3＝90sin(t)，仿真结果如4所示；图4机器人步行轨迹跟踪控制响应曲线，其中图4(a)为关节1轨迹跟踪性能，图4(b)为关节1轨迹跟踪误差；图4(c)为关节2轨迹跟踪性能，图4(d)为关节2轨迹跟踪误差；图4(e)为关节3轨迹跟踪性能，图4(f)为关节3轨迹跟踪误差。

根据图4仿真结果可知，两种控制器都有较好的跟踪控制性能，但在开始阶段，改进控制器具有较快的响应速度，收敛性能也优于参考控制器，并且跟踪误差也比较小，更能满足机器人步行足运动关节对快速性和精度的要求，验证了改进控制器的有效性。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。