一种土体正交异性本构模型的数值分析方法与流程

本发明涉及岩土工程计算机辅助设计技术领域，特别涉及一种土体正交异性本构模型的数值分析方法。

背景技术：

土作为一种非连续摩擦型散粒体工程材料，除表现为非线性非弹性、压硬性、剪胀性、应力-应变与应力历史和应力路径相关性等诸多特性外，在工程实践中，还特别表现出土体的各向异性。土之所以表现出各向异性是由于两种原因：一种是固有各向异性，主要是天然土颗粒在沉积过程中或人工土在填筑过程中水平方向以及垂直方向的排列不同而引起的力学性状和参数的不同；另外一种是应力诱发各向异性，主要是由于土体在各个方向上所受的应力不同，导致土颗粒在空间排列上不同，因而形成各向异性。由于土的成层特性，可以把土体视为正交异性，即平行于沉积面的各个方向的力学特性大致相同，而在垂直于沉积面的方向则表现出不同的特性。

已有研究表明，土体的各向异性对其破坏特性有显著影响，例如，在研究模型条形基础的承载力时，在加载方向和沉积面垂直时得到的最大承载力和在加载方向与沉积面平行时得到的最小承载力差别可以达到34％。对于黏土，强度的各向异性同样很明显。因此，对土体正交异性的合理描述具有重要的工程意义。现有的本构模型多把土体看作连续介质，以经典弹性、弹塑性理论为理论基础，一些大型通用有限元软件，如ANASYS和ABAQUS等，一般只有各向同性弹性、各向同性弹塑性各向异性弹性和各向异性弹塑性等简单的本构关系模型，无法准确反映考虑土体正交异性本构条件下的应力-应变特性。

技术实现要素：

发明目的：本发明针对现有研究的不足，提供了一种土体正交异性本构模型的数值分析方法。

技术方案：本发明提供了一种土体正交异性本构模型的数值分析方法，其特征在于：(1)土体是正交异性材料，其本构模型是基于摩尔-库伦屈服准则建立的；(2)土体正交异性本构模型包括弹性正交异性和塑性正交异性两个方面，并通过双曲线拟合对摩尔-库伦屈服方程进行了修正；(3)土体的正交异性本构模型是通过编译用户材料子程序UMAT，并嵌入到ABAQUS软件中，最终实现土体正交异性本构模拟的数值计算。

所述特征(1)具体为：土体为正交异性材料，即平行于沉积面的各个方向的力学特性大致相同，而在垂直于沉积面的方向则表现出不同的特性。本发明的土体正交异性本构模型是基于摩尔-库伦屈服准则而建立的；

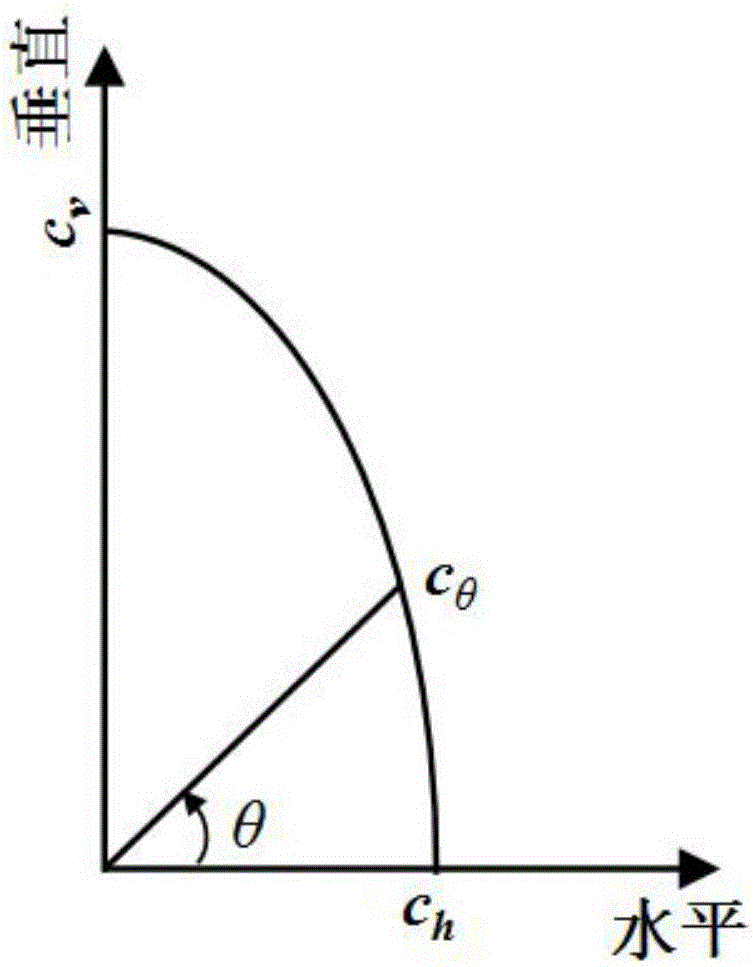
所述特征(2)具体为：土体正交异性模型同时考虑了弹性正交异性和塑性正交异性。弹性正交异性模型包含5个未知量，分别为沉积方向的弹性模量E_v和泊松比υ_vh、垂直于沉积方向的弹性模量E_h和泊松比υ_h、剪切模量G_vh，其他参数可由这5个未知量之间的相互关系得到。塑性本构模型中假定土体内摩擦角为常数，考虑土体粘聚力c存在各向异性效应，且沉积面和垂直于沉积面上的粘聚力c_v、c_h存在关联性，即：c_θ＝c_h+(c_v-c_h)sin²α。由于摩尔-库伦屈服准则在π平面存在六个棱角(奇异点)，使得计算变繁和收敛缓慢，本发明采用双曲线拟合对摩尔-库伦屈服面进行修正，在棱角处得到光滑连续的处理；

所述特征(3)具体为：取塑性势函数与屈服函数的表达式一致，采用隐式后退欧拉算法，对摩尔-库伦屈服函数一次求导、势函数一次求导、势函数二次求导，通过UMAT接口，将编写有土体正交异性本构模型的UMAT子程序嵌入到ABAQUS软件中实现土体正交异性本构模拟的数值计算。

有益效果：本发明克服了ABAQUS自带的摩尔-库伦屈服准则无法同时考虑材料弹性正交异性和塑性各向异性的缺陷，通过编译UMAT子程序将土体正交异性的本构模型嵌入到ABAQUS软件中，实现了土体正交异性本构模拟的数值计算。本发明所提供的数值分析方法能够全面反映土体沉积所引起的正交异性的特点，为合理描述土体正交异性的特性提供了参考，也对指导工程实际问题具有重要的科学价值。

附图说明:

图1为本发明的数值方法流程图；

图2为土体粘聚力随方向的各向异性；

图3为用双曲线近似拟合摩尔库伦屈服函数；

图4为p-q平面摩尔库伦准则的双曲线逼近。

图中，c_v、c_h分别为沉积面和垂直于沉积面上土体的粘聚力，c_θ表示土体在一个与沉积面成θ角的平面上的黏聚力；p为等效压应力；q为Mises等效应力。

具体实施方式

以下结合附图详细叙述本发明的具体实施方式。本发明的保护范围并不仅仅局限于本实施方式的描述。

一种土体正交异性本构模型的数值分析方法，如图1所示流程，具体步骤如下：

(1)根据问题的实际情况，提取结构几何参数，建立ABAQUS有限元模型；

(2)在输入文件中，使用关键词“USER MATERIAL”，表示定义用户材料属性，并根据地质勘测和室内试验结果，将材料参数输入到数值模型中；

(3)在ABAQUS的LOAD模块中，对模型的边界条件进行设置，并施加初始荷载；

(4)选取合适的单元类型划分网格，网格划分前应以划分均匀合格的有限元网格为准则对几何模型进行整理，并进行网格尺寸敏感性分析，以确定同时满足计算精度和计算效率的最优网格划分方式；

(5)编译UMAT用户子程序，并通过ABAQUS主程序接口嵌入到ABAQUS有限元模型中，提交模型并使其运算完成。

所述的一种土体正交异性本构模型的数值分析方法，其特征在于：(1)土体是正交异性材料，其本构模型是基于摩尔-库伦屈服准则建立的；(2)土体正交异性本构模型包括弹性正交异性和塑性正交异性两个方面，并通过双曲线拟合对摩尔-库伦屈服方程进行了修正；(3)土体的正交异性本构模型是通过编译用户材料子程序UMAT，并嵌入到ABAQUS软件中，最终实现土体正交异性本构模拟的数值计算。

所述特征(1)具体为：土体为正交异性材料，即平行于沉积面的各个方向的力学特性大致相同，而在垂直于沉积面的方向则表现出不同的特性。摩尔-库伦屈服准则是目前岩土工程领域应用最广的强度准则之一，并具有两个其他屈服准则无法比拟的优点：第一，它的所有参数都具有直接的物理意义；第二，所有参数均能够由常规的实验方法测得，因此摩尔库伦屈服准则的使用特别简单，本发明的土体正交异性本构模型是基于摩尔-库伦屈服准则而建立的；

所述特征(2)具体为：土体正交异性模型同时考虑了弹性正交异性和塑性正交异性。在弹性阶段，土体的应力-应变关系满足正交异性本构方程，如式(1)所示：

式中，E_v和E_h分别为沉积方向的垂直于沉积方向的弹性模量；υ_vh和υ_h分别为沉积方向的垂直于沉积方向的泊松比；G_h和G_vh分别为沉积方向的垂直于沉积方向的剪切模量。这些弹性参数之间存在一定的关系：

因此，弹性正交异性模型包含了5个未知量，其他的参数可由这5个未知量之间的相互关系得到。

在摩尔-库伦屈服准则中土的强度可以用c与两个参数表示，研究表明，相对于内摩擦角的各向异性，黏聚力c的各向异性效应往往更为显著，可以忽略内摩擦角对于主应力方向的依赖性，而认为黏聚力依赖于主应力方向。因此，这里假定内摩擦角为常数，而考虑c的非均质性与各向异性效应。如图2所示，正交异性土体在各个方向上的粘聚力表示为：

c_θ＝c_h+(c_v-c_h)sin²α (3)

式中，c_v、c_h分别为沉积面和垂直于沉积面上土体的粘聚力，c_θ表示土体在一个与沉积面成θ角的平面上的黏聚力。

若土体服从摩尔-库伦屈服准则，则其用应力不变量表示的正交异性摩尔-库伦屈服方程为：

在有限单元法分析中，由于摩尔库伦屈服准则在π平面上不是正六边形，在拐角处的不连续往往会在数值计算中产生许多问题。当应力状态在这些奇异点处时，由于拐点的存在，屈服函数或势函数存在不连续和梯度无法计算的情况，导致弹塑性应力应变矩阵无法求解。为了避免这种情况，本发明将以应力不变量表示的摩尔库伦准则采用双曲线近似模拟，如图3所示。以图中摩尔库伦准则线作为渐近线，画出在p-q平面上相应的曲线来修正摩尔-库伦准则，最终圆滑屈服面锥体顶点，消除奇异性与子午面拐点不可导的问题，极大地提高了在有限元分析中弹塑性计算的稳定性。图中所对应的参数l、d和h的物理意义分别为

修正后的正交异性摩尔库伦屈服函数的表达式为：

由上式可看出，通过调整参数A可以更好的模拟摩尔库伦屈服函数。在p-q面上，随着参数A的改变，双曲屈服函数与摩尔库伦屈服函数的逼近关系如图4所示。A的取值越小，双曲屈服函数的近似效果越好，当A＝1时，变回原摩尔库伦屈服函数，不再具有消去奇异性的作用。对应在子午面上，摩尔库伦屈服准则是六角锥体，锥体部分用双曲屈服曲线逼近，使锥体变圆滑，让程序在数值计算变得更加稳定。

所述特征(3)具体为：取塑性势函数与屈服函数的表达式一致，即

式中Ψ为土体剪胀角，K(θ)与屈服函数中的表达式相同，将摩擦角改写为Ψ。

在有限元分析中，需要对势函数和屈服函数求偏导，一是用于计算弹塑性应力应变关系，二是在应力迭代算法中用于将应力拉回屈服面。在UMAT子程序编写中，采用隐式后退欧拉算法，对摩尔-库伦屈服函数一次求导、势函数一次求导、势函数二次求导；通过UMAT接口，将编写有土体正交异性本构模型的UMAT子程序嵌入到ABAQUS软件中实现土体正交异性本构模拟的数值计算。