有效减少在量子硬件上模拟费米子哈密顿量所需资源的制作方法

本发明一般涉及量子计算，更具体地涉及有效减少用于在量子硬件上模拟费米子哈密顿量的资源。

背景技术：

在粒子物理学中，费米子是由费米-狄拉克统计表征的任何粒子。这些粒子遵循泡利不相容原则。费米子包括所有夸克和轻子，以及由奇数个这些构成的任何复合粒子，诸如所有重子和许多原子和原子核。费米子与玻色子不同，后者遵循玻色-爱因斯坦统计。费米子可以是基本粒子，例如电子；或者可以是复合粒子，例如质子。根据任何合理的相对论量子场理论中的自旋统计定理，具有整数自旋的粒子是玻色子，而具有半整数自旋的粒子是费米子。

费米子除自旋特性外，还具有守恒的重子或轻子量子数。因此，通常被称为自旋统计关系的，实际上是自旋统计-量子数关系。由于泡利不相容原则，在任何给定时间只有一个费米子可以占据特定的量子态。如果多个费米子具有相同的空间概率分布，则每个费米子的至少一个性质(例如其自旋)必定是不同的。费米子通常与物质有关，而玻色子通常是力载体粒子，尽管在粒子物理目前的状态中，这两个概念之间的区别尚不清楚。在极端条件下弱相互作用的费米子也可能显示出玻色子行为。在低温下，费米子显示出不带电粒子的超流性和带电粒子的超导性。复合费米子，如质子和中子，是日常物质的关键组成部分。

技术实现要素：

按照一个或多个实施例，提供一种计算机实现的减少量子计算机上所需的量子位数的方法。该方法包括根据哈密顿量表征费米系统，该费米系统包括费米子和费米模式，费米模式总数为2m。所述哈密顿量具有由自旋向上和自旋向下奇偶算子编码的奇偶对称性。该方法包括按所述哈密顿量对费米模式进行分类，使得所述2m个模式的前半部分对应于自旋向上，所述2m个模式的后半部分对应于自旋向下，以及使用费米子到量子位映射来变换所述哈密顿量和所述奇偶算子，其中所述费米子到量子位映射将所述奇偶算子变换为量子位m上的第一单量子位泡利算子和量子位2m上的第二单量子位泡利算子。该方法还包括去除已由所述第一单量子位泡利算子操作的所述量子位m和已由所述第二单量子位泡利算子操作的所述量子位2m。

按照一个或多个实施例，提供一种计算机实现的减少量子计算机上所需的量子位数的方法。该方法包括用哈密顿量表征费米系统。所述费米系统包括费米子和费米模式。该方法包括利用费米子到量子位映射转换所述哈密顿量，寻找所述哈密顿量的泡利对称算子，将所述泡利对称算子转换为单量子位泡利算子，以及去除所述单量子位泡利算子正在作用的每个量子位。

按照一个或多个实施例，提供了一种计算机实现的减少量子计算机上所需的量子位数的方法。该方法包括一种计算机实现的减少量子计算机上所需的量子位数的方法，该方法包括根据哈密顿量表征费米系统。所述费米系统包括费米子和费米模式，费米模式总数为2m，其中所述哈密顿量具有粒子数对称性和n个粒子。该方法包括利用从m个费米模式变换到m个量子位的费米子到量子位映射变换所述哈密顿量，其中所述m个量子位由一个计算基础中的m位串表示。该方法还包括将压缩映射应用于所述哈密顿量，使得具有m个量子位的所述哈密顿量被映射到具有q个量子位的变换的哈密顿量，其中q＜m，其中所述压缩映射把标记具有汉明权重n的所述计算基础中的m个量子位的所述m位串映射到q位串。

根据一个或多个实施例，提供了一种系统。该系统包括存储器，该存储器包括用于减少量子计算机上所需的量子位数的计算机可执行指令，以及执行计算机可执行指令的处理器。计算机可执行指令使处理器执行操作。这些操作包括根据哈密顿量表征费米系统，该费米系统包括费米子和费米模式，费米模式总数为2m，所述哈密顿量具有由自旋向上和自旋向下奇偶算子编码的奇偶对称性。这些操作包括按所述哈密顿量对费米模式进行分类，使得所述2m个模式的前半部分对应于自旋向上，所述2m个模式的后半部分对应于自旋向下。这些操作也包括使用费米子到量子位映射来变换所述哈密顿量和所述奇偶算子，其中所述费米子到量子位映射将所述奇偶算子变换为量子位m上的第一单量子位泡利算子和量子位2m上的第二单量子位泡利算子。这些操作还包括去除已由所述第一单量子位泡利算子操作的所述量子位m和已由所述第二单量子位泡利算子操作的所述量子位2m。

根据一个或多个实施例，提供了一种系统。该系统包括存储器，该存储器包括用于减少量子计算机上所需的量子位数的计算机可执行指令，以及执行计算机可执行指令的处理器。计算机可执行指令使处理器执行操作。这些操作包括用哈密顿量表征费米系统。所述费米系统包括费米子和费米模式。这些操作包括利用费米子到量子位映射转换所述哈密顿量，寻找所述哈密顿量的泡利对称算子，将所述泡利对称算子转换为单量子位泡利算子，以及去除所述单量子位泡利算子正在作用的每个量子位。

附图说明

现在将仅通过示例的方式参考附图描述本发明的实施例，其中：

图1是根据一个或多个实施例的约减方案1的流程图。

图2a示出了根据一个或多个实施例的约减方案2的流程图的一部分。

图2b示出了根据一个或多个实施例的约减方案2的流程图的另一部分。

图3a示出了根据一个或多个实施例的约减方案3的流程图的一部分。

图3b示出了根据一个或多个实施例的约减方案3的流程图的另一部分。

图4是示出根据一个或多个实施例的针对小m和n数值计算的q(m，n)的值的表。

图5描绘了根据一个或多个实施例的压缩jordan-wigner变换的曲线图，其具有作为填充分数v＝n/m的函数的量子位-模式比q/m的上限。

图6是根据一个或多个实施例的用于单量子位的二次跳跃项的测量电路。

图7是示出根据一个或多个实施例的从具有n＝3个粒子的m＝14个费米模式到q＝10个量子位的减少的曲线图。

图8是根据一个或多个实施例的被配置为执行约减方案1、2和/或3的计算机的示例。

图9是根据一个或多个实施例的被配置为执行约减方案1、2和/或3的输出的量子计算机的示例。

图10是根据一个或多个实施例的减少(约减方案1)量子计算机上所需的量子位数和/或在量子计算机上的模拟所需的量子位数的方法的流程图。

图11是根据一个或多个实施例的减少(约减方案2)量子计算机上所需的量子位数和/或在量子计算机上的模拟所需的量子位数的方法的流程图。

图12是根据一个或多个实施例的减少(约减方案3)量子计算机上所需的多个量子位数(和/或在量子计算机上的模拟所需的量子位数)的方法的流程图。

具体实施方式

在量子力学中，哈密顿量(hamiltonian)是大多数情况下对应于系统的总能量的算子。它通常用h表示，也用或表示。其频谱是在测量系统的总能量的可能的结果的集合。由于它与系统的时间演化密切相关，因此在量子理论的大多数公式中都具有根本的重要性。

量子信息处理承载解决特定计算问题的希望-对于传统的经典硬件来说这些问题被认为太具有挑战性。特别适用于量子计算机的计算任务是量子力学系统的模拟。这里的中心应用，是可以在例如量子化学、材料科学和核物理中发现的强相互作用的费米系统(fermionicsystems)的模拟。为了在量子计算机上表示费米度(fermionicdegrees)，需要将费米模式(fermionicmodes)映射到作为量子计算的基本逻辑单位的量子位(qubits)。

在现有技术中已知几种将费米自由度(fermionicdegreesoffreedom)映射到量子位自由度(qubitdegreesoffreedom)的变换。最突出的是jordan-wigner变换，其次是计算上更有效的广义jordanwigner变换(bravyi-kitaev映射)和奇偶性(parity)表示。

所有这些变换的共同点是将一个费米自由度(即，一个模式)精确地映射到一个量子位自由度(即，一个量子位)。因此，该映射中所需的量子位的数量等于模式(即，费米模式)的数量。

然而，已知物理费米系统总是服从宇称守恒(parityconservation)，并且，在某些情况下服从更强的粒子数守恒。由于这些对称性，并非所有的自由度在量子位模拟中都是必需的，实际上，一些量子位度(qubitdegrees)编码冗余的信息。一个开放的问题是如何精确地以计算上有效的方式消除这些自由度(即，过量量子位)，其直接转换为在模拟中去除冗余量子位自由度。模拟是在具有量子位的量子计算机上执行的。值得注意的是，量子位是量子计算机中的一个物理量子硬件，量子位是超导量子器件。在哈密顿量中，量子位用作表示物理量子位的术语。

一个或多个实施例提供了一种有效的方案，该方案总是为具有可忽略的自旋-轨道相互作用的任何化学哈密顿量去除两个量子位自由度。一个或多个实施例提供了用于找到隐蔽的对称性的方案，其中每个相互兼容的对称性允许去除哈密顿量中的单个量子位。一个或多个实施例提供压缩方案以减少依赖于粒子数守恒的量子位的数量，并且该压缩方案兼有执行效率和渐进最优。

在若干具体示例中，已经观察到可以在不丢失信息的情况下从模拟中去除各个量子位。这些观察局限于现有技术中非常特定模型的哈密顿量，例如氢分子的量子化学哈密顿量以及具有四个费米模式的费米-哈伯德模型(fermi-hubbardmodel)。在这些例子中，哈密顿量的精确块对角线结构需要是现有技术中已知的。这两种情况都不代表去除通用模型的量子位自由度的计算上有效的方法，因此使得这种消除不可扩展并且使量子位的去除局限于现有技术中考虑的特定模型系统。

然而，实施例讨论了用于在费米子量子模拟中去除量子位的计算上有效的方案，其用于可以在量子化学和材料科学中以及在核物理学的模拟中发现的通用费米量子多体哈密顿量。实施例利用不同的费米映射，例如标准jordan-wigner映射以及广义jordan-wigner映射，以便去除哈密顿量中的量子位自由度。通过去除哈密顿量中的量子位自由度，实施例在执行哈密顿量(在量子位上)期间去除量子计算机(也称为量子硬件、量子机器等)中所需的量子位的数量。对于量子计算机，量子位是一种有价值且昂贵的资源。量子模拟所需的量子位数的减少导致更有效地使用可用资源。这种减少使得能够用相同的量子计算资源模拟比不进行这种减少的情况下所能模拟的更复杂的系统。根据一个或多个实施例，为了在量子模拟中广泛应用，该减少过程需要是高效的，因为低效方案会减弱因使用量子计算机而获得的计算优势。

根据实施例，这些方案的输入是编码要被模拟的系统的哈密顿量。根据实施例，输出是具有减少的自由度(即，对应于需要更少的量子位)的哈密顿量。然后可以将该输出哈密顿量提供给量子算法，该量子算法然后在量子计算机上使用更少的资源。量子算法是发送到量子计算机以解决特定问题的逐步指令的有限序列。在这里，实验者有兴趣获得该输出哈密顿量的基态能量的估计。因此，该输出哈密顿量导致用于量子计算机上的量子模拟的一组输入数据。出于解释目的而非限制，提出了三种方案来消除量子位自由度(这导致量子计算机的硬件中所需的量子位更少)，并且根据实施例在不同的情况下每种方案都有其各自的优点并且工作良好。图8中的计算机800被编程和配置得执行约减方案1、2和3。一个或多个软件应用程序860被编程得具有相应约减方案1、2和3的计算机指令，使得处理器810可以执行它们。在执行相应的约减方案1、2和/或3之后，相应的约减方案1、2和/或3的输出(即，输出哈密顿量)作为需要比原始输入更少的量子位(即，需要比原始哈密顿量更少的量子位)的哈密顿量被施加到图9中的量子计算机900上并执行。应当理解，现有技术的量子计算机仅具有有限数量的在其上进行操作的量子位，例如8个量子位。因此，在8量子位的量子计算机上不能模拟/执行需要10个量子位的哈密顿量，因为量子硬件仅限于8个量子位。实施例被配置为执行缩减(例如，约减方案1、2和/或3)，使得减少的哈密顿量仅需要8个量子位而不是原始的10个量子位，从而创建现在可以在量子计算机的有限的8个量子位上模拟/执行的缩减哈密顿量。因此，实施例通过提供需要较少量子硬件(较少量子位)的技术来改善量子计算机本身的功能。在哈密顿量本来因为太大(即，需要更多量子位(即，量子硬件))而不能应用于量子计算机的有限资源的情况下，实施例通过允许哈密顿量在量子计算机上操作来改进技术。实施例允许缩减复杂的哈密顿量的规模，以便应用于量子计算机。此外，实施例解决了技术中一个根深蒂固的实际问题，即量子计算机具有有限数量的计算资源(即，有限数量的量子位)，而哈密顿量需要比可用的计算资源更多的计算资源。如果无法将哈密顿量缩减到使用较少量子位(量子硬件)的大小，就无法在量子计算机上模拟由哈密顿量表示的系统。

应注意，这里使用的标题和/或副标题，用于下面的解释的目的而非限制。

1)约减方案1：广义jordan-wigner变换中宇称守恒的量子位(parityconservingqubits)的去除。

现在提供约减方案1的高级描述，但是可以在下面找到约减方案1的详细描述。约减方案1保持局部性(locality)，即在广义jordan-wigner变换之后的哈密顿量中的泡利算子的权重，并且从任何保持电子的自旋宇称的任何费米子哈密顿量(fermionichamiltonian)中(精确地)消除两个量子位，从而消除了对量子计算机中的两个量子位的需要。这特别适用于没有自旋轨道耦合的电子结构问题的化学哈密顿量。约减方案1的工作原理如下：哈密顿量作用于自旋轨道的空间2m＝2k(k＝1，2，...)。实验者对轨道进行分类，使得在前的标记1至m都对应于自旋向上(spinup)，而剩余的标记m+1至2m对应于自旋向下(spindown)。现在可以表示前m个自旋向下轨道的奇偶算子(parityoperators)p1和剩余的m个自旋向上轨道的奇偶算子p2。通过用广义jordan-wigner变换将费米模式算子转换为自旋自由度，可以证明第一奇偶算子p1充当量子位m上的简单泡利z-矩阵，即p1＝zm，而第二算子p2是m处和2m处的两个泡利z矩阵的简单乘积，即p2＝zmz2m。由于实验者假设在哈密顿量的每个项中自旋宇称守恒，p1和p2都与变换后的哈密顿量中的每个项交换(commute)。这意味着这个位置(例如，位置m和/或2m)上的泡利算子在每个项中只能是单位矩阵(identitymatrix)或泡利z-矩阵，因为这些是唯一可能在这些位置与p1和p2交换的算子。哈密顿量中每个项的结构现在更简单，因为这些量子位在模拟中的作用是事先已知的(即，预定义的)。因此，由于实验者事先知道电子的自旋宇称(spinparity)，实验者可以去除这两个量子位，并根据宇称(parity)用特征值(+/-1)替换这些项。两个量子位仅在模拟中编码自旋宇称的值，这是在实验者开始模拟之前(即，预定义)已知的信息。去除量子位意味着量子硬件中需要更少的量子位，因此，这相当于直接去除冗余信息。

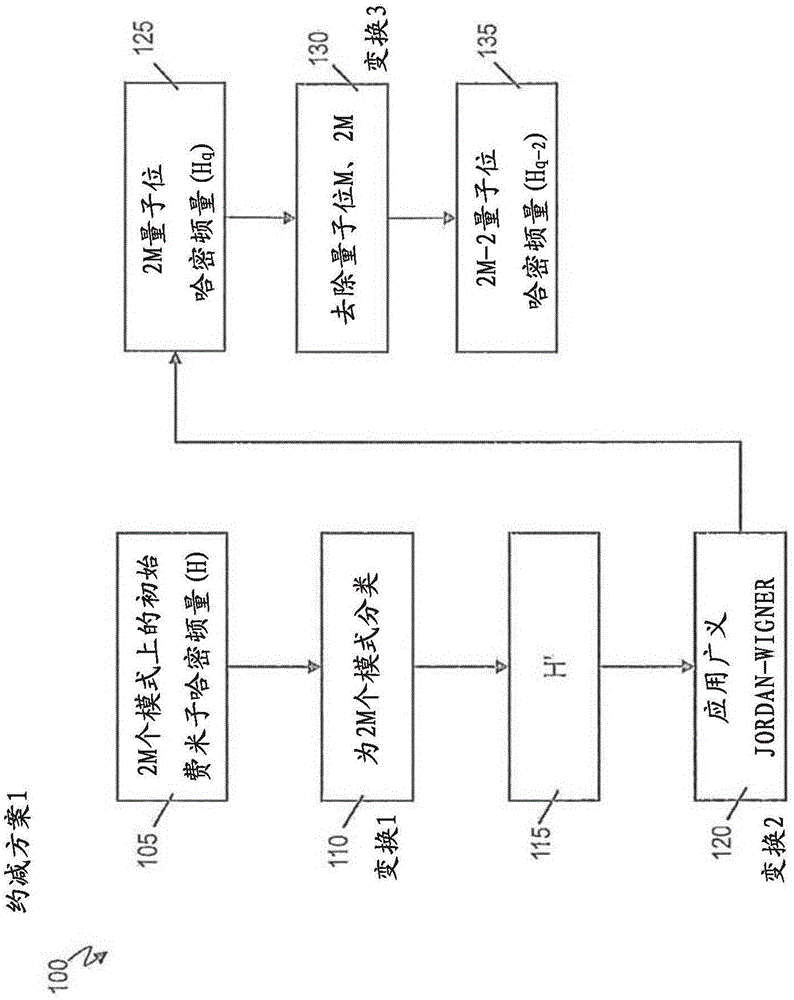
图1是根据一个或多个实施例的约减方案1的流程图100。约减方案1的技术可以(作为应用程序860)在计算机800上执行。给定2m个模式下的初始费米子哈密顿h，比较eq.(方程式)(1)，实验者应用一系列变换1至3将哈密顿量转换为量子位哈密顿量，用于2m-2个量子位的量子模拟。约减方案1在计算机800上执行，而量子模拟(通过减少的哈密顿量，其是需要较少量子位就能执行的哈密顿量)则在量子计算机900的量子硬件上执行。

在框105，计算机800上(通过应用806)的输入是2m费米自旋轨道哈密顿量h(eq.(1))。这是2m个模式下的费米子哈密顿量h。

在框110，计算机800被配置为通过对自旋轨道进行分类并将1...m标记为自旋向下轨道并将m+1...2m标记为自旋向下轨道来从哈密顿量h变换为哈密顿量h’(h→h’)。这是对2至m个费米模式进行分类，并在框115处产生哈密顿量h’。

在框120，计算机800被配置为通过应用广义jordan-wigner(bravyi-kitaev)变换将哈密顿量h’变换为hq(h’→hq)以获得2m量子位哈密顿量hq(在框125)。可以参考《电子结构量子计算的bravyi-kitaev变换》(“thebravyi-kitaevtransformationforquantumcomputationofelectronicstructure”，jacobtseeley，martinjrichard和peterjlove，thejournalofchemicalphysics，137(22)：224109，2012)，在此引用该文作为参考。

在框130，计算机800被配置为通过去除具有标签m的量子位并且去除哈密顿量hq的每个项中具有标签2m的量子位，并且在去除操作之后，将该项乘以适当的特征值+/-1，来将哈密顿量hq变换为hq，-2(hq→hq，-2)。该适当的特征值+/-1是已知的，因为该特征值仅编码自旋宇称的值，后者是在(预定义的)实验者开始模拟之前可用的数据。在框135处，输出是2m-2个量子位哈密顿量hq，-2(参见下面的eq.(6))，其被应用于量子计算机900。

2)约减方案2：通过构造非局部交换泡利矩阵(paulimatrices)来算法减少量子位自由度。

现在提供约减方案2的高级描述，但是可以在下面找到约减方案2的详细描述。约减方案2可以增加变换的哈密顿量的泡利算子的局部性。但是，约减方案2会使哈密顿不变量中被加数的总数减少。量子位哈密顿量被写为泡利矩阵的总和。减少不会改变总和的形式，也不会引入在转换后需要加总的新项。然而，它确实改变了各项的形式，并将泡利算子(paulioperators)映射到每个本身现在共同作用于更多的量子位的泡利算子。约减方案2可以应用于所有被考虑的费米子到量子位变换，特别是广义jordan-wigner变换以及标准jordan-wigner变换。约减方案2的工作原理如下：众所周知，n-量子位泡利群与2n+2个整数拷贝模2的直接群乘积同构。(在数学中，同构是允许反转的同态或态射(即数学映射)。)这种同构可用于将每个泡利(pauli)编码为2n位串，从而丢弃相位依赖性并因此丢弃2个比特。

在已经执行费米模式算子到泡利矩阵的映射之后，可以将该表示排列成二元矩阵。由此，可以通过交换块和转置来构造双奇偶校验矩阵，如在详细的约减方案2中所解释的那样。在有限的比特字段上的该奇偶校验矩阵的核对应于编码与哈密顿量中每个项交换的泡利矩阵的位串(当改变操作数的顺序的改变不会改变结果时，两个元素交换)。注意，内核是该矩阵的零空间，并且核是由矩阵映射到零的所有因子形成的集合。核可以通过简单高斯消元法确定，这是一种有效的约简，并且多项式级地缩减哈密顿量的模式和项的数量。一旦确定了核，就可以很容易地为核中每个线性独立的位串构造一个clifford组元素，以便将相应的非局部泡利算子映射到单量子位泡利矩阵。这个clifford群元素在详细的约减方案2中定义。这个单量子位泡利算子(即，非局部泡利算子)现在通过构造与哈密顿量中的所有项交换，因此实验者再次处于约减方案1的情形中。现在可以去除该量子位，并且可以用相应的(+/-1)特征值替换被去除的量子位，但是与约减方案1不同的是，需要通过模拟来确定特征值。在约减方案1中，可以在实验者通过计算每个自旋轨道中的粒子开始模拟之前计算该值。在目前的约减方案2中，实验者也可以发现事先未知的对称性，该数量是在完成模拟、以使总能量变得最小之后确定的。

图2a和2b描绘了根据一个或多个实施例的约减方案2的流程图200。可以在计算机800上(作为应用程序860)执行约减方案2的技术。给定2m个模式上的初始费米子哈密顿h(比较本文中的eq.(1))，实验者应用变换序列1、2和3来将哈密顿量转换为量子位哈密顿量，用于2m-k个量子位上的量子模拟，其中k由当前的z2对称性确定。如上所述，约减方案2在计算机800上执行，而量子模拟(通过减少的哈密顿量，其是需要较少量子位就能执行的输出哈密顿量)则在量子计算机900的量子硬件上执行。

在框205，计算机800上(通过应用806)的输入是2m费米自旋轨道哈密顿量h(参见本文的eq.(1))。这意味着2m个模式下的费米子哈密顿量h.

在框210，计算机800被配置为通过应用标准jordan-wigner或广义jordan-wigner变换从哈密顿函数h变换到hq(h→hq)，以获得2m量子位哈密顿量(在框215)。这是费米子到量子位的映射。尽管讨论的是标准jordan-wigner和/或广义jordan-wigner(bravyi-kitaev)变换，但应该理解，可以使用其它映射技术，例如，在奇偶基(paritybasis)或任何其它二元基(binarybasis)中作用的映射技术。

从框215分支，计算机800被配置为在框220处将hq中的泡利算子编码为f2奇偶校验矩阵e，并且确定e的核中的泡利算子{gj}的最大交换集合(在框225处)。如果已经找到k＞0个泡利算子，则流程进行到框225。如果没有找到泡利算子，则计算机800被配置为在框221处中止该约减方案。泡利算子{gj}是哈密顿量中的项的对称算子，用于构造一组算子以去除冗余的量子位。如果不能找到对称性，即k＝0，则该方案不能从哈密顿量中去除另外的量子位。

在框230处，计算机800被配置为为每个交换泡利向量{gj}构建clifford映射cj，其中j＝1...k，并且在框235处将clifford变换应用于hq以获得映射gj到位置ml...mk上的单量子位的泡利(paulis)的h’q。

在框235处，计算机800被配置为通过在哈密顿量中找到z2对称性并通过构造clifford变换而从哈密顿量hq变换到h’q(hq→hq’)。z2对称性是指哈密顿量中的对称性。

框235的结果是框240处的2m量子位哈密顿hq’。

在框245处，计算机800被配置以通过去除哈密顿量h’q的每个项中具有标签ml...mk的量子位并将该项乘以适当的特征值+/-1而从哈密顿量h’q变换到h’q，-k(h’q-→h’q，-k)。

在框250处，输出是2m-k量子位哈密顿量hq，-k(参见本文中的eq.(10))，其被应用于量子计算机900。

约减方案3：压缩的jordan-wigner转换，用于保持粒子数的费米子哈密顿量。

现在提供约减方案3的高级描述，但是可以在下面找到约减方案3的详细描述。约减方案3将保持粒子数量的局部费米子算子映射到非局部量子位算子，该算子可以表示为局部泡利算子和非局部对角线算子的乘积。约减方案3分别应用于哈密顿量中的每个项。假设要模拟的费米系统由n个电子占据的m轨道组成，则变换的哈密顿量描述了一个q量子位系统，其中q＜m是m和n的某个函数。实验者为小的m和n值以及详细的约减方案2中q的渐近上界提供了一个函数q(m，n)的值的表(图4中的表4)。特别是，实验者表明，约减方案3允许人们(在量子计算机900上)用小于m-2个量子位完成模拟。约减方案3通过组成标准jordan-wigner变换和线性内射压缩映射来工作，该映射将具有汉明权重n的m位串发送到q位串。实验者利用实用算法来计算压缩映射的逆。变换的哈密顿量具有上述的局部性质，描述压缩映射的二元矩阵是低密度奇偶校验(ldpc)码的奇偶校验矩阵，其将m-q个比特编码为具有最小距离2n+1的m个比特。因此，变换的哈密顿量具有已知的具有恒定编码率的ldpc码的构造和具有恒定分数q/m和n/m的恒定相对距离屈服压缩jordan-winger变换。最后，实验者展示了如何在基于变分方法的量子模拟算法中使用变换的哈密顿量，其中量子计算机(例如，量子计算机900)用于测量给定q-量子位变分状态的能量。

图3a和3b描绘了根据一个或多个实施例的约减方案3的流程图300。可以在计算机800上执行(作为应用程序860的)约减方案3的技术。如上所述，约减方案3在计算机800上执行，而量子模拟(通过减少的哈密顿量，即需要较少量子位的哈密顿量)则在量子计算机900的量子硬件上执行/模拟执行。

图3a描绘了根据一个或多个实施例的哈密顿压缩(第一部分)。在图3a中，在框305处，计算机800被配置为(通过应用程序806)接收具有n个占用费米子的初始m费米自旋-轨道哈密顿量h(参见本文中的eq.(11))的输入。这是具有m个模式和总共n个费米子的哈密顿量h。

在框310处，计算机800被配置为通过将标准jordan-wigner应用于h来将哈密顿函数h变换到hq(h→hq)，以获得m-量子位哈密顿量hq，从而在框315处产生具有n个费米子的hqm量子位旋转哈密顿量。

在框320处，计算机800被配置为将等距u应用于哈密顿量，其源自eq.(16)中的ldpc压缩。作为ldpc压缩的结果，计算机800被配置为在框325处从本文的eq.(13)输出q(m，n)量子位哈密顿量例如，在框325处，计算机800可以从图4的(例如存储在计算机800中和/或被计算机800访问的)表1中读取q(m，n)的值，其具有eq.(12)中的渐近比例(asymptoticscaling)，从而得到图3b中使用的压缩哈密顿量在这种情况下，压缩哈密顿量被用于用图3b中讨论的方案在量子计算机900上的模拟。

图3b描绘了根据一个或多个实施例的压缩测量方案(第二部分)。在量子计算机900上执行(框340的)测量方案以获得作为模拟的一部分的测量值。计算机800用于将获得的值添加到最终结果。不同于图1、2a、2b、3a，图3b在量子计算机900上执行模拟。

在图3b中，在框330处，计算机800被配置为接收压缩哈密顿量的输入，其中具有j＝1...r个项。计算机800设置j＝0且<h>＝0。实验者将<h>定义为从测量数据计算所需的期望值。该值最初设置为零，并作为方案的一部分计算。

在框335处，计算机800被配置为设置j＝j+1，并选择哈密顿项djpj。

量子计算机900被配置为测量(本文中的)eq.(14)中的期望值，然后返回要被应用到计算机800的<djpj>。经典计算机800为量子计算机900提供输入数据以执行模拟。量子计算机900对测量结果进行采样以估计期望值<djpj>。下面在详细的约减方案3中解释获得期望值的测量方案。在框345处，在量子计算机900上(在框340处)执行的这个输出测量数据被反馈到计算机800。

在框345处，计算机800被配置为添加到<h>，其中

在框350处，计算机800被配置为检查是否j＜r。如果是j＜r，过程返回到框335。如果不是，则计算机800被配置为以“否则j＝r”在框355处继续并输出估计<h>。输出是哈密顿量的能量估计<h>。

应当理解，上面已经讨论了对约减方案1、2和3的高级讨论，下面讨论缩减的进一步细节。首先，讨论约减方案1的进一步细节。

详细的约减方案1

实验者现在考虑去除在广义jordan-wigner变换之后保持自旋宇称的分子哈密顿量中的两个量子位的去除。可以参考s.bravyi和a.kitaev的《费米子量子计算》(“fermionicquantumcomputation”)(ann.ofphys.，298(1)：210-226，2002)，其通过引用并入本文。

在第二量化中考虑所涉及的分子哈密顿量的分子轨道。现在，考虑一下最普遍的非相对论费米子哈密顿量，它可以写成

其中是单电子和双电子费米子积分，它遵循有效分子哈密顿量的正确对称性，具有潜在的费米模式的反交换规则和这里的每个分子轨道α是双重自旋退化的，σ＝{↑，↓}标记自旋态，因此eq.(1)中的哈密顿量保持自旋总数。自旋宇称的保持对应于这样的事实，即算子

是哈密顿量的对称性，[p↓↑，h]＝0。为了在量子计算机(例如，量子计算机900)上模拟h，实验者采用广义jordan-wigner变换。该变换将费米子算子映射到中的泡利矩阵的低阶线性组合，其中xi，zi作为总共2m个量子位的第i个量子位上的单量子位泡利-x和泡利-z矩阵。在其原始公式中，该变换要求模式2m的总数是2的幂，即2m＝2^k，k＝1，2，...。实验者从现在开始作此假设。这种广义的jordan-wigner映射可以表述为

实验者选择了2m费米模式的顺序，使得以及关于量子位u(i)、p(i)和p(i)的更新、奇偶性和剩余子集的定义，参见《用于电子结构的量子计算的bravyi-kitaev变换》(thebravyi-kitaevtransformationforquantumcomputationofelectronicstructure)。这个变换将哈密顿函数h映射到hermitian泡利向量的总和，这样实验者就可以用量子位自由度来将h写成

其中和ha∈r可以从哈密顿系数hα，β，uαβγμ计算出，作为线性组合。可以验证，按照eq.(3)，对称算子p↓↑将变换到

p↑＝zm和p↓＝z2mzm.eq.(5)

由于实验者知道[p↓↑，h]＝0和p↑＝zm以及p↓p↑＝z2m是单量子位算子，它们与哈密顿量中的每个项交换，使得对于所有a，[p↓↑，σa]＝0。注意这些算子是单量子位算子、很大程度上取决于2m是2的幂的事实。然而，在某些情况下，可以为不再满足该标准的模式数量的执行广义jordan-wigner变换的一个版本。在这种情况下，p↓↑的泡利表示将变为非本地化的并包含更高权重的泡利算子。然而，在这种情况下，可以找到一个能将这些对称性再次映射到局部泡利的clifford变换，这将在下面针对约减方案2的段落中进行解释。返回到约减方案1，因为编码这种对称性的最终泡利算子在哪一种情形中都是单量子位泡利，实验者可以用它们的特征值代替这些算子，这只取决于自旋向上↑和自旋向下↓轨道中的电子数量n。实验者知道在没有自旋耦合的分子哈密顿量的情况下的这个数量，其中↑、↓状态中的总自旋自由度的数量是hq的对称性。p↑，p↓的特征值为±1，因此可以在每个泡利算子中进行求值并表示为这样就可以将2m量子位哈密顿量减少到2m-2个量子位上的hq，-2

这里的σa\{m，2m}，意思是量子位m、2m被从σ_a中去除。应该理解，eq.(6)是约减方案1中的方框135的最终结果。

现在，转至约减方案2，上面提供了对约减方案2的高级讨论，现在在下文提供约减方案2的进一步细节。

详细的约减方案2

该约减方案可视为约减方案1的概括。约减方案2可以应用于标准或广义jordanwigner变换。对标准jordan-wigner变换的引证可以在e.wigner和p.jordan的“daspaulische”(z.phys，47∶631，1928)中找到，其通过引用结合到本文中。虽然该文仅以德文发表，英文翻译是eugenep.wigner和p.jordan的“aboutthepauliexclusionprinciple“(关于泡利排除原则)，(z.phys47.631(1928)：14-75)。假设存在具有m个模式的费米子哈密顿量，以便实验者可以通过上述变换将其映射到

其中又是h_a∈r和σ_a∈p_m。实验者现在寻找k个哈密顿交换泡利算子它们构成哈密顿hq的子集对称性，使得和如果找到一些对称性gj，则实验者为它们中的每个(gj)构建一个clifford变换其将gj映射到位置j处的单量子位泡利矩阵。然后，对于每一个gj，实验者搜索作用于位置mj的单量子位泡利矩阵为使得且

对于每对实验者将clifford操作定义为

其中使得

实验者现在可以将哈密顿量h映射到

其现在有单量子位的泡利算子作为对称性。通过与约减方案1中相同的参数，可以从hq中去除在上支持的量子位，并将其替换为它们的特征值(±1)。

因此，最初定义为对m个量子位起作用的哈密顿量现在可以在m-k个量子位上表示。

也就是说，实验者可以写出

该约减方案2的方案包括约减方案1作为特例。然而，可能发生的是，clifford操作将从广义jordan-wigner变换获得的低权重哈密顿量映射到非本地算子，这取决于感兴趣的特定问题。应该认识到，框250中的2m-k量子位哈密顿量是如eq.(10)中的hq，-k所定义的。

算子gj可以从与泡利矩阵集相关联的奇偶校验矩阵e构造。之间众所周知的同构可用于构造(2m)×#{a∈hq}维二元码矩阵g＝[gz，gx]。该矩阵g＝[gz，gx]是列空间中所有σa的编码位串的集合。然后通过交换泡利算子{g_j}_(j＝1，...，k)跨越双奇偶校验矩阵的上的核。

最后，上文提供了对约减方案3的高级讨论，下文不提供约减方案3的进一步细节。

详细的约减方案3

这个减少适用于保持粒子总数的一般费米子哈密顿量。设m和n分别为费米子模数和粒子数(占有模式)。实验者考虑被基础状态|x1，x2，...，xm>跨越的fock空间的n-粒子扇区，其中x_α＝0，1是模式α的占有数，注意，m现在表示模式的总数(包括自旋在内)。我们的目标是模拟费米子哈密顿量

其中，每个项vj的形式为或≤m，并且hj是实系数。不失一般性，n≤m/2。否则，对所有交换粒子和孔的α执行变换这里，实验者描述压缩jordan-wigner变换，它将h映射到描述q＜m的量子位系统的新哈密顿量其中q＝q(m，n)是m和n的某个函数。的基态能量(groundstateenergy)与限制在n-粒子扇区(sector)的h的基态能量一致。图4示出针对小的m和n数值计算的q(m，n)的值。图4是代表压缩jordan-wigner变换的表1。表1表示，具有m模式和n个粒子的费米系统可以在具有q+1个量子位的量子计算机上模拟，其中q＝q(m，n)。应该记得q表示在压缩之后表示哈密顿量所需的量子位数。而m表示可以被总共n个费米子占据的或总共n个费米子中的费米模式的原始数量。表1示出了左列中的n和顶行中的m的一组对的q(m，n)的值。

实验者还导出在m，n趋向无穷大、使得填充分数(fillingfraction)v＝n/m保持不变的情况下q(m，n)的渐近上界。也就是说，实验者表明，对于任何常数0＜v＜1/4都有

q≤6vmexp[h(2v)/3v-1]，eq.(12)

其中h(x)＝-xlog(x)-(1-x)log(1-x)是香农(shannon)熵函数(实验者这里使用自然对数)。量子位-模式比q/m被示为图5中的填充分数v的函数。图5描绘了具有来自eq.(12)的量子位-模式比q/m的上限的压缩jordan-wigner变换的曲线图，其是极限m，n→∞时填充分数v＝n/m的函数。可以看出，只要v低于阈值v0≈0.057，则q/m＜1。实验者不期望eq.(12)中的界限紧。随着量子化学哈密顿量的专业化，模拟所需的量子位数是q(m，n↑)+q(m，n↓)，其中m是空间轨道的数量(即，模式数量的一半)，n↑↓是具有自旋向上和自旋向下的电子的数量。为了描述新哈密顿量实验者引入了更多的符号。对于每个项vj，令vj＝0，1，2是可以被移动vj的最大粒子数。换句话说，所有对角算子都具有vj＝0，跳跃(hoppig)和受控跳跃算子具有vj＝1，而双跳算子具有vj＝2。则

其中，汉密顿算子dj，pj具有以下属性：

(1)dj是具有矩阵元素0，±1的对角算子。

(2)pj是权重最多为6vj的x-型泡利算子。

(3)pjdj＝djpj。

eq.(13)中的系数hj与eq.(11)中的相同。假设目标是估计的基态能量。实验者考虑变分方法(variationalapproach)，其中用量子计算机900来测量可在可用量子硬件(即量子计算机)上准备的某个固定q量子位状态ψ的能量(变分方法的示例，可以参考d.wecker、mbhastings和m.troyer所著的“towardspracticalquantumvariationalalgorithms”(走向实际量子变分算法)(见于arxivpreprintarxiv：1507.08969，2015)，其通过引用并入本文。)然后用合适的经典优化算法使能量在某变分状态ψ上最小化。通过线性化，单独为每个j(即，为哈密顿量中的每项)分别测量能量<ψ|djpj|ψ>就足够了。考虑某固定项djpj并重新标记量子位，使得pj作用于前w个量子位，其中w≤6v_j。然后pj＝x1x2…xw。作为如上所述在量子计算机900上执行的框340的进一步细节，实验者引入在|+>状态下初始化的辅助量子位a。针对j＝1，...，w，实验者用量子计算机900应用具有控制量子位a和目标量子位j的cnot门。cnot门是一个两个量子位的单元运算，称为受控非门，如果源量子位是1，则在目标量子位上施加非(not)。接下来，实验者测量x-基中的量子位a。设σ＝±1为测量结果。注意，σ与pj的特征值相符，这是因为cnots将量子位a上的单量子位x传播到量子位1，...，w上的x的乘积。其次，测量z-基础中的所有量子位1，...，q。该测量的结果是位串x∈{0，1}^q。由于dj和pj交换，所以得到

其中期望值取自x和σ的测量统计。总的来说，图3b中的压缩测量方案需要q+1个量子位。通过量子计算准备变分状态ψ需要q个量子位，额外的量子位用来应用恒定数量的cnot门以在量子计算机900上获得测量结果。

新哈密顿量被定义为其中u是将m模式fock空间的n-粒子扇区映射到q个量子位的hilbert空间等距(单一嵌入)。实验者设置

其中a是稍后要选择的大小为q×m的二元矩阵。这里si＝0，1和|s1，...，sq>是q个量子位的基态。设w(m，n)为具有汉明权重n的所有m位串的集合：

w(m，n)＝{x∈{0，1}^m：|x|＝n}.

下面，实验者使用简写符号u|x>＞＝|s>和s＝ax，其中x∈w(m，n)。为了使u成为等距(isometry)，矩阵a必须将不同的向量x∈w(m，n)映射到不同的q-位向量s。换句话说，需要以下内射性条件：

对于x，y∈w(m，n)如果ax＝ay则x＝y.eq.(16)

可以容易地检查eq.(16)相当于

此处的ker(a)是a的核，即使得ax＝0的m-位向量x的集合。如果某矩阵a满足eq.(16)或eq.(17)，则称该矩阵a是n-内射的。只要a是描述二进制线性码的奇偶校验矩阵-该二进制线性码将m-q个比特编码成具有最小距离2n+1的m个比特-则满足n-内射性条件。实际上，在这种情况下，所有权重高达n的误差必定具有不同的综合征(syndromes)，因此，综合征s＝ax唯一地标识权重-n的误差x。

要计算需要一个用于的明确公式。定义一个集合ω＝a·w(m，n)。换句话说，对于某个x∈w(m，n)，如果s＝ax，则s∈ω。令x(s)为ω的指标函数，即，如果s∈ω则x(s)＝1，否则x(s)＝0。设f：ω→w(m，n)为为一个“解码”映射，使得f(ax)＝xforallx∈w(m，n).

由于eq.(16)中的内射性条件，该解码映射是明确定义的。对于所有x∈w(m，n)且对于所有s∈{0，1}^q，实验者获得

(对于此处的f(s)可以任意定义。)设c(a)为a的列的最大权重，

首先考查跳跃项不失一般性，α≤β。定义

算子z(α，β)和πα，β作用于q个量子位的希尔伯特空间(hilbertspace)。设z(α，α)＝i且πα，α＝|1><1|α。运用eq.(18)，可以很容易确定

其中a¹，...，a^m是被认为是q位串的a的列，表示按位异或，并且

d(s)＝x(s)<f(s)|z(α，β)πα，β|f(s)>∈{0，±1}.eq.(22)

实验者得出的结论是其中dj是使得<s|dj|s＞＝d(s)的对角算子并且pj将泡利x应用到支持的每个量子位。算子pj的权重最多为2c(a)，参看eq.(19)。注意，notethatdjpj＝pjdj，因为当vj是受控跳跃项时，如果用|1><1|γπα，β替换πα，β，则该情形类似于上述情况。最后，考查双跳跃项其中α＜β＜γ＜δ。用eq.(18)可以很容易地确定

其中

d(s)＝x(s)<f(s)|z(α，β)z(γ，δ)παβ，γδ|f(s)>eq.(24)

且

παβ，γδ＝|11><11|α，β|00><00|γ，δ+|00><00|α，β|11><11|γ，δ.

注意，d(s)取值0，±1。实验者得出结论其中dj是使得<s|dj|s>＝d(s)的对角算子，并且pj将泡利x应用于支持的每个量子位。算子pj的权重最多为4c(a)。因此，新的哈密顿函数h具有如上所述的形式(回想一下：(1)dj是具有矩阵元素0，±1的对角算子；((2)pj是权重最多为6vj的x型泡利算子；(3)pjdj＝djpj。)

算子pj是权重的x型泡利算子

|pj|≤2vjc(a).eq.(25)

由于u是等距，哈密顿量h和的非零特征值是相同的。因此，实验者总是可以假设h的基态能量是负的(否则用h-λh代替h，其中λ是大的正常数)。因此h和具有相同的基态能量。

为了最小化能量测量所需的cnot数量，实验者要最小化算子pj的权重，即二量子位单元操作-被称为受控非门-的数量。等效地，实验者要保持列权重c(a)小，参看eq.(25)。因此，剩下的任务是构造具有小的恒定列权重c(a)和最小可能行数q的n-内射矩阵a。从eq.(17)推断，a的所有列必定是不同的，这只有当c(a)≥2时才有可能。首先假设c(a)＝2，即a的每列最多有两个非零元素。这样的矩阵可以被视为具有q个顶点和m个边的图ga的入射矩阵，使得如果第j个边入射到第i个顶点，则ai，j＝1。(具有权重-1的a的列表示仅具有一个端点的“悬空”边。)使用eq.(17)，当且仅当图形ga没有长度2，4，...，2n的循环时，可以检查a是n-内射的(回想一下，如果任何顶点具有来自边c的偶数个入射边，则边c的子集称为循环)。然而，这个条件太严格了。实际上，图ga的平均顶点度是d≥2m/q。为了实现恒定的量子位-模式比q/m＜1，实验者利用具有平均顶点度d＞2的图族。使用摩尔界限[6]可以很容易地证明这样的图ga中的顶点数必定是n指数。换句话说，只有当n＝o(log(m))时，才能实现恒定的量子位-模式比q/m＜1，实际利益有限。

以下，实验者关注下一个最简单情形，即c(a)＝3。由eq.(15)得|pj|≤6vj。具有恒定比率q/m＜1，n/m＞0且c(a)＝3的n-内射矩阵a的无限族可以由具有恒定编码率和线性距离的低密度奇偶校验(ldpc)码构成。(ldpc码的示例，可以参考r.gallager的《低密度奇偶校验码》(“low-densityparity-checkcodes”，informationtheory，iretransactionson，8(1)：21-28，1962，在此参考引用)。尽管在该示例中使用了低密度奇偶校验码，但是应当知道，如本领域技术人员所理解的那样，可以使用其它压缩码。具体而言，实验者断言，对于任何常数0＜v＜1/4，对于所有(预定义的)足够大的m，以及所有的n＜vm，存在c(a)＝3、大小为q×m的n-内射矩阵a，其中q满足eq.(15)。实际上，考虑某固定对q，m并设a是大小为q×m的随机二元矩阵，使得a的每列从w(q，3)上的均匀分布中得出。a的所有列都是独立的。通过联合界限，a不能成为n-内射的概率上限可以为

其中p(q，2k)是从w(q，3)上的均匀分布中抽取的2k个独立向量之和等于零模2的概率。实际上，eq.(17)暗示，对于某x∈w(m，2k)且1≤k≤n，除非ax＝0，否则a是n-内射的。因此，支持x的a的列的总和等于零。该联合界限于是意味着eq.(26)。采用在此参考引用的r.darling、m.penrose、a.wade和s.zabell的《稀疏随机gf(2)矩阵中的秩缺陷》(“rankdeficiencyinsparserandomgf(2)matrices”，inelectron.j.probab，19(83)：1-36，2014)的引理3.1，得到

其中

这里应理解，除非0≤k≤n，否则用斯特林的公式可以得到一个界限

这里，e≡exp(1)。将eq.(28)代入eq.(27)，得到

其中h(x)是香农熵函数。因此，只要h(2v)+3vlog(η)＜0，则pfail＜1，相当于eq.(12)。由于pfail＜1，必定存在至少一个具有c(a)＝3和q个行的n-内射矩阵a，其中q满足eq.(12)。

需要指出的是，选择足够大的常数c(a)可以任意接近gilbert-varshamov界限，即q≤m(h2(2n/m)+∈)，其中是二元香农熵函数，并且通过选择足够大的c(a)可以使∈＞0任意小。该断言源于(预定义的)良好ldpc码的存在，例如参见《低密度奇偶校验码》的定理a.3。

图4中的表中所示的q(m，n)的值，是通过数值搜索具有c(a)＝3和最小可能q的n-内射矩阵a获得的。具体地，实验者最大化目标函数f(a)，该函数被定义为集合a·w(m，n)中的不同元素的数量。注意，当且仅当(iff)集合a·w(m，n)的所有元素都是不同的，即则a是n-内射的。使用模拟退火算法的一个版本，函数f(a)在满足c(a)＝3的所有二元矩阵的集合上最大化。

最后，实验者展示了如何计算解码映射f(s)。假设a是大小为q×m的固定n-内射矩阵。给定一个字符串s∈{0，1}^q，必须找到x∈w(m，n)，使得s＝ax或判断不存在这样的字符串x，即要分解n＝n1+n2，其中，如果n为偶数，n1，2＝n/2，如果n为奇数，n1，2＝(n±1)/2。对于每个i＝1，2，设ti为存储每个u∈w(m，ni)的综合征t＝au的查找表。ti的条目按字典顺序排序。设ui是将每个条目t∈ti映射到字符串u∈w(m，ni)使得t＝au的查找表。注意，上述u是唯一的，因为由于eq.(17)，a是ni-内射的。表ti，ui可以在量子模拟之前由(在量子计算机900上)计算机800计算，因为它们仅依赖于a。首先假设，对于某个x∈w(m，n)，s＝ax。考虑任何分解其中ui∈w(m，ni)且设ti＝aui。于是，表t1和t2必定分别包含条目t1和对于每个t1∈t1，要检查t2是否包含由于表t2是排了序的，用二元搜索就看在时间o(|t1|log|t2|)内完成。假设如上所述地找到了t1，t2，则使用表ui来找到使得ti＝aui的ui。然后且由此得出和具有2到2n之间的均匀权重。从eq.(17)可以推断并完成。在剩余的情况下，如果没有找到如上所述的对t1，t2，则可以推断ax＝s对于x∈w(m，n)无解。上述算法对于中等规模的系统是实用的，例如-但不限于-m≤50的系统。实际上，对于m≤50来说，由于m≤n/2，表ti，ui的大小最多为通常，计算解码映射f(s)可能看起来是困难的计算问题，因此下面提供两个用于解释目的而非限制的示例。

约减方案3：实施例1

实验者考虑这种减少的最简单的例子。实验者考虑单个电子n＝1，其具有八个轨道m＝8，如图4中表1的左上角所示。在本节的约减方案3之后，这8个状态(即，m＝8)上的可以被压缩到3个量子位上的8个状态，即如图4的表1中所示。这是通过应用下面的eq.(30)中的压缩矩阵a将8个状态压缩到3个量子位而得出的。这种情况具有特别容易通过的优点，尽管它可能看起来有点误导，因为实验者只构造8个模式中的单粒子状态的二进制编码作为压缩。通常，如上所述，情况并非如此，并且结果严重依赖于ldpc码以确保低的权重和效率。现在，实验者继续详细地进行压缩。

因此，实验者考虑将w(8，1)中的位串压缩到q(8，1)-量子位。这是通过对每个x∈w(8，1)应用奇偶校验矩阵a∈m3×8(f2)来获得集合ω来而完成的。这个例子的相关基础状态只是由w(8，1)中的位串在第二次量化中编码的8个单粒子状态，是

这个代码的最简单的矩阵a是简单地通过二进制编码从上面的8位字符串中从0，...，7计数的粒子的位置而得出的，因此，可以写记为

由此，实验者可以立即读出集合ω，其由a的二进制列向量给出。二进制列向量是a的具有满足二进制代数的条目0，1的列。对于每个s∈ω，解码映射f是通过计算二进制数s的十进制表示并在正确的位置中选择具有一的8位串来定义的。因此，等距u作用于例如x＝(00000100)上，如|101>＝u|00000100>，而所有其它不在w(8，1)中的位串则被映射到零，如u|10100000>＝0。共轭是类似地构建的。

通过这种映射，实验者现在可以讨论在哈密顿量和图6中的测量电路600中出现的项。为了说明这种编码的工作方式，实验者考察一个简单的二次跳跃元素即实验者考查粒子从第5模式到模式3的跳跳跃和共轭。回想一下，对于不同的s值，对s∈ω标记的状态的作用是

简单起见，将电路600视为具有量子位(例如，本例中为4个量子位)和4个单独地测量每个量子位的输出的测量装置(例如，光子测量装置)的量子计算机。出于解释的目的，为了便于理解，电路600被示为简单的量子计算机，不过应当理解，可以同样地使用量子计算机900。电路600如上所述地测量期望值<ψ|vj|ψ>＝e[σ·<s|dj|s)]，如上所述。实验者需要q(m，n)+1个量子位，因此这里在电路600中示出有4个量子位，但应该理解的是，在电路600中可以使用超过4个量子位。首先，实验者要确定pj中的泡利x算子的支持，其由以下的位值给出：

因此，根据上面介绍的惯例，泡利-x贡献由pj＝x2x3给出。因此，图6给出了测量djpj并让实验者采样e[σ·<s|dj|s>]的示例电路600。图6是用于具有由w(8，1)给出的并且被压缩为q(8，1)＝3个量子位的位表示的八个模式中的单量子位的二次跳跃项的测量电路600。电路600中的每条线对应于单量子位。3个底部量子位处于变分状态psiψ，而顶部量子位在正(+)状态被初始化。然后应用两个受控非操作(cnot)，如始于控制量子位(顶部量子位)上的黑点、终于作为目标量子位的两个底部量子位的水平线所示。然后在计算基础中测量所有量子位之前，将hadamard门应用于顶部量子位。hadamard门是执行称为hadamard变换的单元变换的单量子位门h。

图6中的电路600的测量结果由四位给出，其中辅助位s0用于计算其余三位(s1，s2，s3)＝s通过公式d(s)＝x(s)<f(s)|z(α，β)πα，β|f(s)>确定d(s)＝<s|dj|s>，其中f(s)是解码映射。在这种情况下，如上所述，解码映射相当简单。

实验者现在讨论电路600的一些可能的测量结果。可以假设从电路600获得的第一测量结果是然后，实验者(在计算机800上)计算σ＝1并且d(1，1，0)＝<0001000|z3，5∏3，5|0001000>＝1，因此实验者可以将σ·<s|dj<s|＝1添加到平均值。对于第二次测量，假设实验者从电路600获得字符串对此，实验者可以以相同的方式(在计算机800上)计算出σ＝-1但d(1，0，0)＝0，因为解码状态|f(1，0，0)>＝|01000000>被π3，5湮灭，因此该测量结果不会对期望值产生影响。通常，实验者从由电路600(或量子计算机900)准备的压缩状态u|ψ>开始进行采样，直到估计出具有足够统计精度(可以提前预先确定)的期望值e[σ·<s|dj|s>]。

约减方案3：实施例2

为了考虑稍微更复杂的例子，实验者明确地描述了从m＝14个费米模式的系统到q＝10个量子位的系统的减少。实验者假设粒子数是n＝3。考虑如图7中的图所示的具有10个顶点和14个边的图。图7是描述从具有n＝3个粒子的m＝14个费米模式到q＝10个量子位的减少的图表700。(在现有技术中，因为存在14个费米模式，在诸如电路600或量子计算机900的量子计算机中将需要14个量子位。)然而，由于约减方案3，设计了利用更少的量子位(例如，本例中是10个量子位)的实施方式。fock基矢量|x1，...，x14>被映射到量子位状态|s1，...，s10>，其中si等于入射到si的所有边上的xj的和(模2)。只要图700没有长度为2、4或6的循环，就满足内射性条件eq.(17)。

在图7中，每个顶点表示一个量子位i∈{1，...，q}，而每个边表示一个费米模式j∈{1，...，m}。实验者将综合征si和费米子占用数xj分别与图的顶点和边相关联。接下来是选择eq.(15)中的奇偶校验矩阵a作为图700的入射矩阵。换句话说，综合征si等于位于入射到顶点i的边上的变量xj的和(模2)。例如，s1＝x1+x2(mod2)，s2＝x2+x3+x9(mod2)等。实验者需要检查a是否满足内射性条件eq.(16)。如上所述，查验a的核不包含权重2，4或6的向量就足够了，参见eq.(17)。直接检查显示，图7所示的图700不包含长度为2，4或6的循环(回想一下，如果任何顶点具有偶数个来自x的入射边，则边x的子集称为循环)。由于选择a作为图700的入射矩阵，因此方程式ax＝0等于x是个循环。因此，ax＝0意味着|x|≠2，4，6，满足内射性条件eq.(17)。应当理解，该示例非常大，因此，缩减矩阵是以最简单的表达方式-即用图700-提供的，以便于理解。这提供了图4中的表1中的压缩的一个示例，其中n＝3且m＝14，使得q＝10。电路测量需要从图8中的经典计算机800生成，然后在图9中的量子计算机900上运行。

标题和/或副标题中断。图10是根据一个或多个实施例的减少(约减方案1)量子计算机900上所需的量子位数(和/或模拟所需的量子位数)的方法1000的流程图。

在框1005，计算机800被配置为用哈密顿量表征(或描述)费米系统，该费米系统包括费米子和费米模式，总共有2m个费米模式，其中哈密顿量具有由通过自旋向上和自旋向下奇偶算子编码的奇偶对称性。

在框1010，计算机800被配置为对哈密顿量上的费米模式进行分类，使得2m个模式的前半部分对应于自旋向上，2m个模式的后半部分对应于自旋向下。

在框1015，计算机800被配置为利用费米子到量子位映射来变换哈密顿量和奇偶算子，其中费米子到量子位映射将奇偶算子变换为量子位m上的第一单量子位泡利算子和量子位2m上的第二单量子位泡利算子。

在框1020，计算机800被配置为去除已由第一单量子位泡利算子操作的量子位m和已由第二单量子位泡利算子操作的量子位2m。

另外，费米子到量子位映射是广义jordan-wigner变换。

量子位m上的第一单量子位泡利算子是量子位m上的泡利z矩阵。量子位2m上的第二单量子位泡利算子是量子位m位置和量子位2m位置的两个泡利z矩阵的乘积。

去除已由第一单量子位泡利算子操作的量子位m包括根据量子位m的奇偶性(parity)用特征值+1或-1替换量子位m。去除已由第二单量子位泡利算子操作的量子位2m包括根据量子位2m的奇偶性用特征值+1或-1替换量子位2m。量子位m编码量子位m的奇偶性，量子位2m编码量子位2m的奇偶性。量子位m和量子位2m的奇偶性是预先已知的。

量子计算机900被配置为执行/模拟具有减少的量子位的哈密顿量。

图11是根据一个或多个实施例的减少(约减方案2)量子计算机900上所需的量子位数(和/或模拟所需的量子位数)的方法的流程图1100。

在框1105处，计算机800被配置为根据哈密顿量来表征(或描述)费米系统，该费米系统包括费米子和费米模式。

在框1110处，计算机800被配置为利用费米子到量子位映射来变换哈密顿量。在框1115，计算机800被配置为寻找哈密顿量的泡利对称算子。

在框1120，计算机800被配置为将该泡利对称算子变换为单量子位泡利算子。在框1125，计算机800被配置为去除该单量子位泡利操作符正在作用的每个量子位。

费米子到量子位映射是广义jordan-wigner变换或标准jordan-wigner变换。

寻找哈密顿量的泡利对称算子包括：在哈密顿量上执行奇偶校验矩阵以确定泡利对称算子，如果没有找到泡利对称算子，则确定不能进行进一步的缩减；如果找到了泡利对称算子，则确定泡利对称算子的交换集。将泡利对称算子变换为单量子位泡利算子包括：为该泡利对称算子的交换集构造clifford变换，以把该泡利对称算子的交换集映射到单量子位泡利算子。

图12是根据一个或多个实施例的减少(约减方案3)量子计算机900上所需的量子位数(和/或模拟所需的量子位数)的方法的流程图1200。

在框1205，计算机800被配置为根据哈密顿量表征(或描述)费米系统，费米系统包括费米子和费米模式，总共有m个费米模式，其中哈密顿量具有粒子数对称性和n个粒子。

在框1210，计算机800被配置为利用从m个费米模式变换到m个量子位的费米子到量子位映射来变换哈密顿量，其中m个量子位由一个计算基础中的m-位串表示。

在框1215，计算机800被配置为将压缩映射应用于哈密顿量，使得具有m个量子位的哈密顿量被映射到具有q个量子位的变换的哈密顿量，其中q<m，其中该压缩映射把标记具有汉明(hamming)权重n的计算基础中的m个量子位的m位串映射到q位串。

对于m个量子位中的每一个，计算基础是0和1。量子计算机900被配置为测量具有q个量子位的变换的哈密顿量的能量，该量子计算机包括q+1量子位上的量子测量电路。作为由量子计算机900测量的测量的能量，计算机800被配置为接收变换的哈密顿量的每个压缩项的测量的能量，对测量的能量执行解码以获得哈密顿量中的每个未压缩项的测量结果，以及在应用压缩映射之前，将测量结果组合以获得哈密顿量的能量。

变换的哈密顿量包括压缩的项，并且在应用压缩映射之前的哈密顿量包括未压缩的项。

图9是根据实施例的可以处理约减方案1、2和/或3的输出的量子计算机900(量子硬件)的示例。通常，量子计算机是遵循满足divincenzo标准的量子力学定律的任何物理系统。这些标准设定对被视为量子计算机的量子力学系统的要求。标准包括(1)具有良好表征的量子位的可扩展物理系统；(2)能将量子位状态初始化为简单基准状态；(3)长相关退相干时间；(4)量子门的“通用”集合；(5)量子位特定的测量能力；(6)能互换静止的和飞行的量子位；以及(7)能在指定位置之间忠实地传输飞行量子位。

图9中的量子计算机900示出了作为控制程序的输入905、控制信号910、量子位915、读出信号920和作为输出的测量数据925。作为满足这些要求的量子力学系统，量子计算机900(以及量子计算机600)被配置为接收控制信号910作为输入905信息(即，约减方案1、2和/或3)以应用量子门(quantumgates)序列并应用测量操作。不同量子位915之间的量子门通过它们的相互作用930而调节。测量算子产生经典信号(作为测量数据925)，其可以由控制系统-即量子计算机900-的的实验者读取。

现在转向图8，该图示出了一例计算机800，例如，被配置为执行本文所讨论的约减方案1、2和/或3以使得约减方案1、2和3的结果可以输入到量子计算机600、900的的任何类型的计算机系统。计算机800可以是一台以上计算机上的分布式计算机系统。这里讨论的各种方法、过程、模块、流程图、工具、应用、电路、元件和技术也都可以包含和/或利用计算机800的能力。实际上，可以利用计算机800的能力来实现本文所讨论的示例性实施例的诸要素。

总的来说，就硬件架构而言，计算机800可包括一个或多个处理器810、计算机可读存储器820以及经由本地接口(未予示出)可通信地耦合的一个或多个输入和/或输出(i/o)设备870。本地接口可以是例如-但不限于-如本领域中已知的一个或多个总线或其它有线或无线连接。本地接口可以具有用以实现通信的附加元件，例如控制器、缓冲器(高速缓存)、驱动器、中继器和接收器。此外，本地接口可以包括地址、控制和/或数据连接，以实现上述部件之间的适当通信。

处理器810是用于执行可以存储在存储器820中的软件的硬件设备。处理器810实际上可以是任何定制的或商业途径可得到的处理器、中央处理单元(cpu)、数据信号处理器(dsp)、或者是与计算机800相关联的几个处理器中的辅助处理器，并且处理器810可以是基于半导体的微处理器(微芯片的形式)或宏处理器。

计算机可读存储器820可包括以下的任何一种或组合：易失性存储器元件(例如随机存取存储器(ram)，诸如动态随机存取存储器(dram)、静态随机存取存储器(sram)等)和非易失性存储器元件(例如，rom、可擦除可编程只读存储器(eprom)、电可擦除可编程只读存储器(eeprom)、可编程只读存储器(prom)、磁带、光盘只读存储器(cd-rom)、磁盘、磁带、盒式磁带等)。此外，存储器820可以包含电、磁、光和/或其它类型的存储介质。注意，存储器820可以具有分布式架构，其中各种组件彼此远离，但是可以被处理器810访问。

计算机可读存储器820中的软件可以包括一个或多个单独的程序，每个程序包括用于实现逻辑功能的可执行指令序列。存储器820中的软件包括合适的操作系统(0/s)850、编译器840、源代码830、以及示例性实施例的一个或多个应用程序860。如图所示，应用程序860包括用于实现示例性实施例的元素、过程、方法、功能和操作的许多功能组件。

操作系统850可以控制其它计算机程序的执行，并提供调度、输入-输出控制、文件和数据管理、存储器管理以及通信控制和相关服务。

应用程序860可以是源程序、可执行程序(目标代码)、脚本或包括要执行的一组指令的任何其它实体。如果是源程序，则该程序通常通过可以包括在存储器820中的编译器(例如编译器840)、汇编器、解释器等进行翻译，以便与操作系统850一起正确地操作。此外，应用程序860可以被编写为(a)具有数据和方法的类的面向对象的编程语言，或者(b)具有例程、子例程和/或函数的过程编程语言。

i/o设备870可以包括输入设备(或外围设备)，例如-但不限于-鼠标、键盘、扫描仪、麦克风、相机等。此外，i/o设备870还可以包括输入设备870。包括输出设备(或外围设备)，例如-但不限于-打印机、显示器等。最后，i/o设备870还可以包括传送输入和输出的设备，例如-但不限于-nic或调制器/解调器(用于访问远程设备、其它文件、设备、系统或网络)、射频(rf)或其它收发器、电话接口、桥接器、路由器等。i/o设备870还包括用于通过各种网络(例如因特网或内联网)进行通信的组件。i/o设备870可以利用蓝牙连接和电缆(通过例如通用串行总线(usb)端口、串行端口、并行端口、firewire、hdmi(高清多媒体接口)等)，连接到处理器810和/或与处理器810通信。

在应用程序860以硬件实现的示例性实施例中，应用程序860可以用以下技术中的任何一个或组合来实现，这些技术在本领域中都是众所周知的：具有用于在数据信号上实现逻辑功能的逻辑门的离散逻辑电路，具有适当的组合逻辑门的专用集成电路(asic)，可编程门阵列(pga)，现场可编程门阵列(fpga)，等等。

已经出于说明的目的给出了对本发明的各种实施例的描述，但是并不旨在穷举或限制于所公开的实施例。在不脱离所描述的实施例的范围的情况下，许多修改和变化对于本领域普通技术人员来说是显而易见的。选择这里使用的术语是为了最好地解释实施例的原理、实际应用或对市场中的技术的技术改进，或者使本领域普通技术人员能够理解本文公开的实施例。

本发明可以是任何可能的技术细节集成级别的系统、方法和/或计算机程序产品。计算机程序产品可以包括计算机可读存储介质(或介质)，其上具有计算机可读程序指令，用于使处理器执行本发明的各方面。

计算机可读存储介质可以是有形设备，其可以保留和存储指令以供指令执行设备使用。计算机可读存储介质可以是例如一但不限于一电子存储设备、磁存储设备、光存储设备、电磁存储设备、半导体存储设备或前述的任何合适组合。计算机可读存储介质的更具体例子的非详尽列表包括：便携式计算机磁盘、硬盘、随机存取存储器(ram)、只读存储器(rom)、可擦除可编程只读存储器(eprom或闪存)、静态随机存取存储器(sram)、便携式光盘只读存储器(cd-rom)、数字通用光盘(dvd)、记忆棒、软盘、机械编码装置-例如在其上记录有指令的凹槽中的穿孔卡或凸起结构，以及前述的任何合适的组合。这里使用的计算机可读存储介质不应被解释为暂时性信号本身，例如无线电波或其它自由传播的电磁波，通过波导或其它传输介质传播的电磁波(例如，通过的光脉冲)光纤电缆)或通过电线传输的电信号。

本文描述的计算机可读程序指令可以经由网络从计算机可读存储介质下载到相应的计算/处理设备或下载到外部计算机或外部存储设备。网络例如是因特网、局域网、广域网和/或无线网络。网络可以包括铜传输电缆、光传输光纤、无线传输、路由器、防火墙、交换机、网关计算机和/或边服务器。每个计算/处理设备中的网络适配器卡或网络接口从网络接收计算机可读程序指令，并转发计算机可读程序指令以存储在相应计算/处理设备内的计算机可读存储介质中。

用于执行本发明的操作的计算机可读程序指令可以是汇编指令、指令集架构(isa)指令、机器指令、机器相关指令、微代码、固件指令、状态设置数据、集成电路配置数据、或者以包括诸如smalltalk、c++等的面向对象的编程语言以及诸如“c”编程语言的过程编程语言或类似的编程语言的一种或多种编程语言的任意组合编写的源代码或目标代码。计算机可读程序指令可以完全在用户的计算机上、部分在用户的计算机上、作为独立的软件包、部分地在用户的计算机上部分地在远程计算机上或完全在远程计算机或服务器上执行。在后一种情况下，远程计算机可以通过包括局域网(lan)或广域网(wan)的任何类型的网络连接到用户的计算机，或者可以(例如，利用互联网服务提供商通过互联网)连接到外部计算机。在一些实施例中，包括例如可编程逻辑电路、现场可编程门阵列(fpga)或可编程逻辑阵列(pla)的电子电路可以通过利用计算机可读程序指令的状态信息来执行计算机可读程序指令来个性化来电子电路，以执行本发明的各方面。

这里参考根据本发明实施例的方法、装置(系统)和计算机程序产品的流程图和/或框图来描述本发明的各方面。将理解，流程图图示和/或框图的每个框以及流程图图示和/或框图中的框的组合可以由计算机可读程序指令实现。

这些计算机可读程序指令可以被提供给通用计算机、专用计算机或其它可编程数据处理装置的处理器以产生机器，使得通过计算机的处理器或其它可编程数据处理装置执行的指令创建用于实现流程图和/或框图的框中指定的功能/动作的手段。这些计算机可读程序指令还可以存储在计算机可读存储介质中，该计算机可读存储介质可以指示计算机、可编程数据处理装置和/或其它设备以特定方式起作用，使得具有存储在其中的指令的计算机可读存储介质包括一种包括实现流程图和/或框图的框块中指定的功能/动作的各方面的指令的制品。

这些计算机可读程序指令也可以被加载到计算机、其它可编程数据处理装置或其它设备上，以使得在计算机、其它可编程装置或其它设备上执行一系列操作步骤以产生计算机实现的过程，使得在计算机、其它可编程装置或其它设备上执行的指令实现在流程图和/或框图的框中指定的功能/动作。

附图中的流程图和框图显示了根据本发明的多个实施例的系统、方法和计算机程序产品的可能实现的体系架构、功能和操作。在这点上，流程图或框图中的每个方框可以代表一个模块、程序段或代码的一部分，所述模块、程序段或代码的一部分包含一个或多个用于实现规定的逻辑功能的可执行指令。也应当注意，在有些作为替换的实现中，方框中所标注的功能也可以以不同于附图中所标注的顺序发生。例如，两个连续的方框实际上可以基本并行地执行，它们有时也可以按相反的顺序执行，这依所涉及的功能而定。也要注意的是，框图和/或流程图中的每个方框、以及框图和/或流程图中的方框的组合，可以用执行规定的功能或动作的专用的基于硬件的系统来实现，或者可以用专用硬件与计算机指令的组合来实现。