基于Chebyshev正交多项式扩展RTSKalman平滑方法与流程

本发明涉及导航制导与控制中的航空航天系统信息处理的技术领域，尤其涉及一种基于chebyshev正交多项式扩展rts(rauch-tung-striebel)kalman平滑方法，对运动载体的即时定位与地图构建(simultaneouslocalizationandmapping，slam)slam问题进行平滑处理。

背景技术：

根据估计时刻用到的观测量信息情况，最优估计理论分为预测、滤波和平滑三种类型，其中滤波计算是利用当前时刻以及以前时刻的所有观测信息对当前系统状态变量进行估计计算，而平滑方法除了利用滤波计算用到的观测信息，还要用到当前时刻以后的部分或者所有观测信息。因此，理论上平滑方法是一种离线处理方法，在滤波计算基础上对系统状态变量进一步做出改善，从而获得更加精确的计算数据结果。

平滑算法和滤波算法一样，其理论基础也是基于bayesians最优滤波理论，假设系统状态变量满足高斯分布。平滑估计算法一般可分为固定点平滑、固定滞后平滑和固定区间平滑等，其中固定区间平滑是利用某一时间区间内的所有观测信息对所有状态变量进行估计计算的一种方法，其应用范围最为广泛，而rauch-tung-striebel平滑算法就是一种固定区间平滑计算方法，但是传统的平滑算法都是针对线性系统状态变量开展滤波后的平滑操作，但是近年来也有很多种非线性平滑算法，如其中应用最广泛的基于taylor级数扩展表达式的一阶或者二阶rts非线性平滑算法，被称为扩展rts平滑算法，以及基于sigma点非线性rts平滑算法、中心差分rts平滑算法、gauss-hermite数值积分逼近的rts平滑算法和容积rts平滑算法等。

技术实现要素：

针对传统的平滑算法都是针对线性系统状态变量开展滤波后平滑操作的技术问题，本发明提出一种基于chebyshev正交多项式扩展rtskalman平滑方法，将chebyshev正交多项式的优异性质应用于slam问题系统设计中，实现slam系统非线性模型状态参数最优滤波平滑计算，具有较好的计算优势和计算效能。

为了达到上述目的，本发明的技术方案是这样实现的：一种基于chebyshev正交多项式扩展rtskalman平滑方法，其步骤如下：

步骤一：建立slam系统的非线性的状态模型，包括状态方程和非线性观测方程；

步骤二：对非线性slam系统状态模型的状态变量参数的kalman滤波计算，经由k＝t步迭代计算获得第t步的最优滤波结果，并存储各个时刻的估计数据；

步骤三：从k＝t开始，对步骤二获取的各个时刻滤波的估计数据开展逆向平滑操作，基于chebyshev多项式拟合逼近slam系统的非线性状态方程，实施chebyshev多项式逼近计算操作，根据第t步滤波数据，计算平滑算法的预测均值、预测方差矩阵和协方差矩阵；

步骤四：计算chebyshev多项式拟合逼近计算的平滑增益，获取非线性系统方程的chebyshev多项式拟合逼近计算的平滑均值及平滑方差矩阵；

步骤五：令k＝t-1，根据t-1步的估计数据再次开展chebyshev多项式rts平滑计算，获得t-1步的chebyshev多项式拟合逼近的平滑均值和方差；进而计算直至k＝0时的chebyshev多项式拟合逼近平滑数据，从而完成slam问题系统状态参数变量的平滑计算任务。

所述步骤一中slam系统的非线性的状态模型为

其中，xk∈rⁿ是第k步的系统状态变量，yk∈r^m是第k步的系统观测变量，rⁿ和r^m分别表示n和m维的实数空间，qk-1～n(0，qk-1)和rk～n(0，rk)分别表示高斯过程噪声和观测噪声，qk-1表示系统状态变量第k-1步的过程噪声方差，rk表示系统观测变量第k步的过程噪声方差，f(·)和h(·)分别表示系统模型的动态模型函数和观测模型函数。

所述步骤三中从k＝t-1开始，利用第k步的估计数据mk|k和pk|k，利用chebyshev多项式拟合逼近计算第k+1步组合导航系统状态变量的预测均值为：

mk+1|k＝e[f(xk)|mk|k,pk|k]

利用有限n项的chebyshev多项式逼近整理可得到：

进一步整理可以获得预测均值表达式为，

其中，表示第k步已知均值mk|k表达的矩阵矩阵表示为：

利用chebyshev多项式拟合逼近组合导航系统状态变量的平滑预测方差矩阵，由第一算法的卷积计算获得系数矩阵v0:nn，系统状态变量的预测方差矩阵表达为：

其中，qk表示系统状态变量的过程噪声方差；v0:2n＝conv(b0:n,b0:n)，b0:n为chebyshev多项式第k步的系数：b0:n＝[a0-mk+1|k,a1,a2,…,an]；

协方差矩阵ck+1|k计算为：

所述第一算法为：

首先利用chebyshev多项式的系数赋值v0:nn←b0:n；

从i＝1到n-1，计算卷积v0:nn＝conv(v0:nn,b0:n)；其中，conv(·)表示卷积计算；

经过n-1步迭代计算获得系数向量v0:nn。

所述步骤三中利用chebyshev多项式拟合逼近slam系统非线性状态方程开展多项式拟合逼近计算操作：利用有限n项chebyshev多项式开展slam系统状态方程拟合逼近计算为：

其中，y＝f(x)表示slam系统状态方程的非线性项，g(x)表示有限n项chebyshev多项式函数；且在自变量x的取值区间[-1,1]上，n+1个chebyshev多项式系数cj为：

那么，

所述有限n项chebyshev多项式整理获得：

其中，c0:n＝[c0,c1,…,cn]是chebyshev级数多项式的系数项，an矩阵由chebyshev系数组成，表示矩阵an的第n列向量：

其中，列向量是由n阶chebyshev多项式中的包括第n个单项式的所有系数组成。

所述步骤三中计算slam系统状态方程拟合逼近的预测均值：非线性函数y的一阶矩期望均值可写为

其中，mi表示随机变量δx的第i阶矩，上式可整理为：

系数是一个下三角矩阵，将其整理为

其中，

其中，⊙表示hadamard乘积符号，是一个常值矩阵，通过构建第n+1行向量

将rn行向量截断来获取矩阵的其他行向量。

所述步骤四中平滑增益gk为：

计算第k+1步的平滑均值为：

mk+1|k+1＝mk|k+gk(xk+1-mk+1|k)；

相应的平滑方差矩阵为：

最终经由t步迭代平滑计算获得系统状态变量的平滑均值和方差矩阵分别为：

mk|t＝mk|k+gk(xk+1|t-mk+1|k)

本发明的有益效果：利用chebyshev多项式扩展逼近slam问题系统的非线性多项式模型方程，利用chebyshev多项式拟合slam问题系统的模型方程，实现slam问题系统状态向量的滤波平滑计算，从而达到进一步改善slam问题系统状态变量参数最优估计的精度要求。经由机器人slam系统仿真实验，并与传统的扩展kalman平滑算法对比，验证了本发明的计算优势和计算效能。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

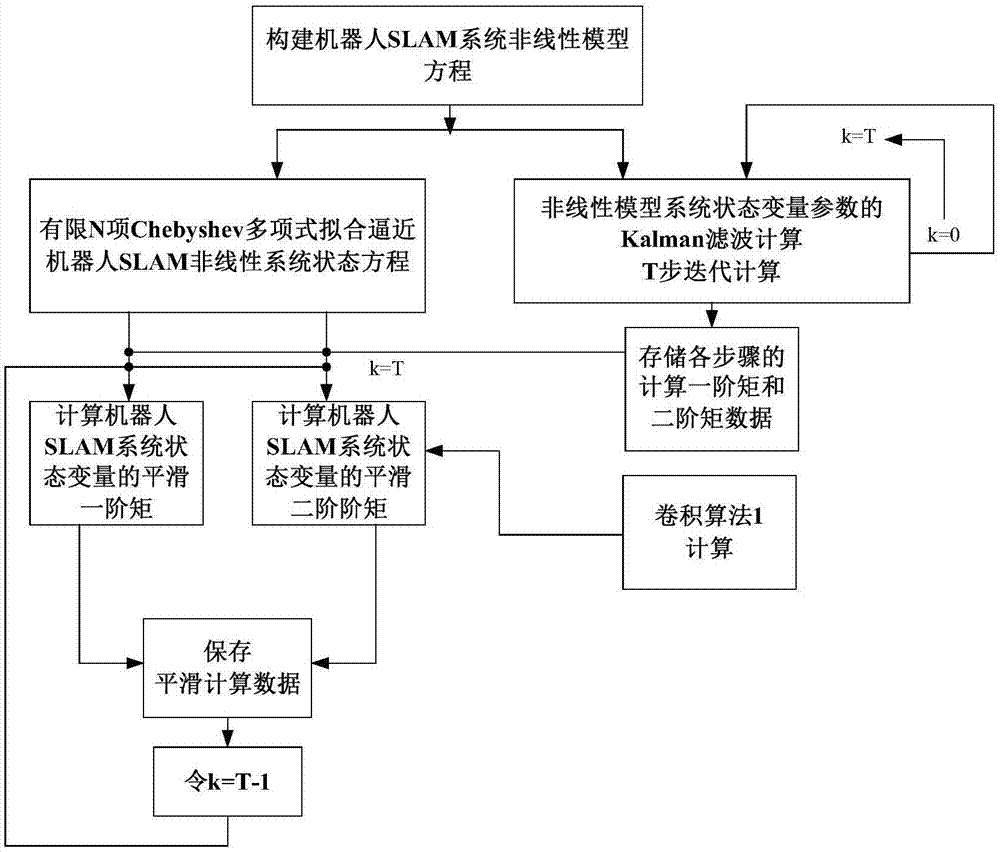
图1是本发明的流程图。

图2是本发明在机器人slam仿真环境设置场景中的应用实例，描述了本发明平滑计算获得的载体运动平滑曲线与实际运动轨迹的对比图，图中曲线如图注所示。

图3是本发明对机器人slam系统的处理结果，上图为处理后获得的机器人位置误差，下图为机器人x和y两个方向的标准差数据曲线。

图4是利用扩展kalman平滑算法计算机器人slam系统的平滑运动轨迹曲线和真实运动轨迹曲线对比图。

图5是利用扩展kalman平滑算法计算机器人slam系统的位置误差和机器人x和y方向的标准差数据曲线。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明提出的基于chebyshev正交多项式扩展rtskalman平滑方法，经由系统非线性函数的chebyshev正交多项式扩展逼近计算获得非线性系统函数的最优平滑，以slam问题系统离散化的随机状态空间模型为：

其中，xk∈rⁿ是第k步的系统状态变量，yk∈r^m是第k步的系统观测变量，qk-1～n(0，qk-1)和rk～n(0，rk)分别表示系统高斯过程噪声和观测噪声，qk-1表示系统状态变量第k-1步的过程噪声方差，rk表示系统观测变量第k步的过程噪声方差，f(·)和h(·)表示系统模型的动态模型函数和观测模型函数。

平滑算法一般都是用于改善滤波结果的再平滑计算过程，平滑计算在数学上就是在给定所有观测向量{yk}(t>k)基础上的系统状态变量的条件概率分布p(xk|y1：t)(k＝1,2,…,t)的集合。本发明中利用高斯分布假设推理过程，也就是系统状态变量满足高斯正态分布：

p(xk|y1:t)＝n(xk|mk|t,pk|t)(2)

其中，mk|t是系统状态变量的均值向量，pk|t是第k步平滑计算获得的逼近高斯分布的系统状态变量的方差矩阵。但是在滤波和平滑操作中都需要计算系统非线性函数的一阶和二阶矩，如针对满足高斯分布的泛指非线性向量函数g(x)，

其中，表示非线性函数g(x)的期望，。但是对于大多数的非线性函数g(x)而言，式(3)、(4)和(5)这三类矩的精确计算几乎是不可能的，因此，很多文献提出了多种逼近计算方法，如taylor级数扩展法、sigma点法、gauss-hermite数值积分逼近法、中心差分逼近法和容积点逼近法以及粒子群逼近计算法等等。本发明给出bayesian平滑的理论计算步骤，假设已经获得了第k步系统状态变量的滤波解的高斯逼近，

p(xk|y1:k)＝n(xk|mk|k,pk|k)(6)

那么泛指非线性函数的高斯一阶矩(期望值)可表示为，

平滑算法从时刻k＝t的滤波结果开始平滑计算，直至k＝0为止，从而高斯分布的bayesian平滑计算框架为：

其中，pk|k为估计方差矩阵，pk+1|k为预测方差矩阵，pk+1|t表示第k+1步chebyshev多项式拟合逼近状态变量的平滑方差矩阵，mk+1|k为计算平滑算法的预测均值，mk|k为估计均值、mk+1|t表示第k+1步chebyshev多项式拟合逼近的状态变量的平滑均值，ck+1|k为计算平滑算法的协方差矩阵，gk为chebyshev多项式拟合逼近计算的平滑增益，表示平滑增益矩阵gk的转置。

最终获得系统状态变量逼近计算的平滑分布：

p(xk|y1:t)≈n(xk|mk|t,pk|t)(9)

本发明利用chebeshev多项式逼近计算实现非线性系统函数扩展rts平滑计算，有效减小了基于taylor级数的扩展表达式计算的复杂性和计算量；假设非线性slam问题系统方程为f(x)是非线性非多项式函数，若存在着一个n阶chebyshev多项式函数g(x)，其自变量x满足x∈[-1,1]，chebyshev多项式定义为

tn(x)＝cos(narccos(x)),n＝1,2,…(10)

相邻的三个切比雪夫多项式具有递推关系，可以表达为

切比雪夫多项式具有一个重要性质就是正交性，切比雪夫多项式是采用n次的切比雪夫多项式加权代数式来逼近任意的非线性函数，这些加权多项式满足正交特性，在chebyshev多项式零点上，其正交性可表达为

切比雪夫多项式t(x)具有奇偶性，满足

tn(-x)＝(-1)ⁿtn(x)，(13)

切比雪夫多项式满足t(x)∈[-1,1]取值区间，并且在此区间中t(x)具有n+1个不同的实数零点，可由这些零点实施切比雪夫多项式插值逼近计算操作。

根据chebyshev多项式的奇偶性质及取值特性，chebyshev多项式还可以写为

其中，αn,i表示n次chebyshev多项式的第i阶单项式的系数，αn,n-2i也是同样的意义，表示n次chebyshev多项式的第n-2i阶单项式的系数，式中[n/2]表示取整数，从而也可以获得两项chebyshev多项式的乘积表达式为：

同时切比雪夫多项式函数在区间[-1,1]上交替出现n+1个极值点组，其最大值为1，最小值为-1。切比雪夫多项式的最高次项系数为2^n-1，(n＝1,2,···)。从而切比雪夫多项式存在着与零偏差最小的特性，并且其偏差为依此特性可以在切比雪夫多项式逼近非线性函数过程中获得多项式插值余项的极小值，这有助于有效改善扩展rts平滑算法的计算精度。

在实际应用过程中，一般取有限n项chebyshev多项式插值逼近非线性系统函数，有限n项的chebyshev多项式逼近为

其中，在自变量x的取值区间[-1,1]上，n+1个chebyshev多项式系数cj可写为

那么

另外一般情况下系统状态变量的取值区间不在[-1,1]区间，这时需要做系统状态变量的变量替换，若系统状态变量取值区间为[a,b]，一般可采用变量替换表达式

那么相应的插值零点变换为：

由此可以开展chebyshev多项式逼近非线性函数的一阶矩期望和二阶矩方差矩阵的计算工作。

假设利用chebyshev多项式g(x)拟合非线性泛指函数y＝f(x)，那么f(x)可简单表达为，

这里c0:n＝[c0,c1,…,cn]是由式(17)计算获得的chebyshev级数多项式的系数项，而an矩阵是由chebyshev系数组成，则表示矩阵an的第n列向量，其定义为

其中，列向量是由n阶chebyshev多项式中的包括第n个单项式的所有系数组成。

假设自变量x满足高斯分布那么自变量x可以表示为其中δx是满足分布的零均值高斯随机变量，自变量的幂次项表示为

其中是两项式的系数项，从而利用式(22)可以整理式(20)为

那么非线性函数y的一阶矩期望均值可写为

其中，mi表示随机变量δx的第i阶矩，那么由式(21)可以整理式(24)为

应该说明的是，是一个下三角矩阵，为了减小计算量，将其整理为

其中，

其中，⊙表示hadamard乘积符号。应该说明的是，利用这种分解计算，是一个常值矩阵，对于矩阵，仅通过构建其第n+1行向量将rn的行向量截断来获取矩阵的其他行向量。

利用chebyshev多项式的性质实施函数y＝f(x)的方差矩阵的逼近计算。若chebyshev多项式的系数可表示为：

那么函数y＝f(x)的n阶逼近中心矩(n>1)，如可以表达为：

其中，系数向量v0:nn可由第一算法来实现。第一算法可简单描述：首先利用chebyshev多项式的系数赋值v0:nn←b0:n；从i＝1到n-1，计算卷积v0:nn＝conv(v0:nn,b0:n)；经过n-1步迭代计算，最后获得系数向量v0:nn。其中，符号conv(·)表示卷积计算。

其实在滤波和平滑计算中使用的是一阶矩和二阶矩，在这里考虑n＝2时的方差矩阵计算，此时那么经由第一算法解算整理式(28)可以获得二阶矩方差的计算，

那么协方差也可以计算为，

如图1所示，一种基于chebyshev正交多项式扩展rtskalman平滑方法，首先建立非线性slam问题系统的状态方程和观测方程；实施非线性slam问题系统状态模型的状态变量参数的kalman滤波计算，经由k＝t步迭代计算获得第t步的最优滤波结果估计均值mt|t和估计方差矩阵pt|t，并存储各个时刻的估计数据mk|k和pk|k；然后从k＝t-1开始，基于chebyshev多项式拟合逼近slam问题系统非线性的状态方程和观测方程，实施chebyshev多项式逼近计算操作，计算平滑算法的预测均值mk+1|k、预测方差矩阵pk+1|k和协方差矩阵ck+1|k；接着计算chebyshev多项式拟合逼近计算的平滑增益gk，获取非线性系统的状态方程和观测方程的chebyshev多项式拟合逼近计算的平滑均值mk|t以及平滑方差矩阵pk|t，从而完成slam问题系统状态参数变量的估计计算任务。具体步骤为：

步骤一：建立slam系统的非线性的状态模型，包括状态方程和非线性观测方程。

构建slam系统的模型为式(1)，其参数如前所述。

步骤二：对非线性slam系统状态模型的状态变量参数的kalman滤波计算，经由k＝t步迭代计算获得第t步的最优滤波结果，并存储各个时刻的估计数据。

经由k＝t步的kalman滤波迭代计算获得系统状态变量的最优滤波结果为估计均值mt|t和估计方差矩阵pt|t，并存储各个时刻的估计数据mk|k和pk|k。

步骤三：从k＝t开始，对步骤二获取的各个时刻滤波的估计数据开展逆向平滑操作，基于chebyshev多项式拟合逼近slam系统的非线性状态方程，实施chebyshev多项式逼近计算操作，根据第t次滤波数据，计算平滑算法的预测均值、预测方差矩阵和协方差矩阵。

从k＝t-1开始，基于chebyshev多项式拟合逼近slam问题系统非线性状态方程和观测方程，实施chebyshev多项式逼近计算操作，计算平滑算法的预测均值mk+1|k，预测方差矩阵pk+1|k和协方差矩阵ck+1|k。

从k＝t-1开始，利用第k步的估计数据mk|k和pk|k，利用chebyshev多项式拟合逼近计算第k+1步组合导航系统状态变量的预测均值为：

mk+1|k＝e[f(xk)|mk|k,pk|k](31)

利用式(16)整理可得到

利用式(23)-(26)，进一步整理可以获得预测均值表达式为，

其中，表示第k步已知均值mk|k表达的矩阵，类似于式(26)可表示为，

利用chebyshev多项式拟合逼近组合导航系统状态变量的平滑预测方差矩阵，利用式(29)，经由第一算法的卷积计算获得系数矩阵v0:nn，系统状态变量的预测方差矩阵表达为：

其中，qk表示系统状态变量的过程噪声方差；v0:2n＝conv(b0:n,b0:n)，b0:n如式(27)所述，在第k步具体表达为

b0:n＝[a0-mk+1|k,a1,a2,…,an](36)

相应的协方差矩阵ck+1|k可由式(30)计算为，

步骤四：计算chebyshev多项式拟合逼近计算的平滑增益，获取非线性系统方程的chebyshev多项式拟合逼近计算的平滑均值及平滑方差矩阵。

接着计算chebyshev多项式拟合逼近计算的平滑增益gk，获取非线性系统方程和观测方程的chebyshev多项式拟合逼近计算的平滑均值mk|t，以及平滑方差矩阵pk|t。

考虑平滑增益gk计算：

计算第k+1步的平滑均值为，

mk+1|k+1＝mk|k+gk(xk+1-mk+1|k)(39)

相应的平滑方差矩阵为，

最终经由t步迭代平滑计算获得系统状态变量的平滑均值和方差矩阵为，

mk|t＝mk|k+gk(xk+1|t-mk+1|k)(41)

从而完成rts固定区间平滑算法的迭代计算过程。

步骤五：令k＝t-1，根据t-1次的估计数据再次开展chebyshev多项式rts平滑计算，获得t-1次的chebyshev多项式拟合逼近的平滑均值和方差；进而计算直至k＝0时的chebyshev多项式拟合逼近平滑数据，从而完成slam问题系统状态参数变量的平滑计算任务。

具体实例：考虑机器人运动载体的即时定位与地图构建(simultaneouslocalizationandmapping,slam)slam问题，在笛卡尔坐标系下可以给出载体运动方程为，

这里slam系统状态向量为xk＝[xk,yk,φk]^t分别表示k时刻的载体位置坐标和方位；v是载体速度，g表示载体转向角，参数wb表示载体轮距，噪声向量vk是高斯过程噪声，vk～n(0,qk)，其中，qk表示噪声方差。

机器人运动载体配备了距离和方位传感器，能够在方位角±30°范围内感知距离30m范围内的目标物体，由此可以获得机器人slam系统的观测方程为，

这里(ri,x,ri,y)是传感器感知的路标位置坐标，wk是观测白噪声，满足分布wk～n(0,rk)，其中rk表示观测噪声方差。那么slam系统初始参数设置为：初始速度v0＝3m/s，g＝±30°，wb＝4m，速度标准差σv＝0.3m/s，转向角标准差σg＝3°，距离标准差σr＝0.1m，方位标准差σb＝1°。初始状态向量x0＝0，初始方差p0＝diag{10^-10,10^-10,10^-10}。由此展开仿真验证工作，并且把chebyshev多项式扩展rts平滑算法和扩展kalman平滑算法计算效能对比，如图2、3、4、5所示。对比图2和图4，很明显两种算法中chebyshevrts平滑器算法与机器人真实运行轨迹数据拟合程度较好，而扩展kalman平滑器算法的拟合程度比较差些；从图3和图5可以对比看出，chebyshevrts平滑器算法的计算标准差比较小，误差数据曲线平滑稳定，而扩展kalman平滑器算法获得的位置误差数据变化剧烈，甚至出现数据发散现象，明显误差数据比较大，相应的标准偏差数据较大，通过利用这两种平滑器算法开展机器人slam系统仿真实验，获得的实验数据说明，chebyshevrts平滑器算法计算效能优于常规的扩展kalman平滑算法，表现出了chebyshevrts平滑器算法的计算优势。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。