一种结合随机变量灰性和贝叶斯模型修正的不确定性参数估计方法与流程

本发明涉及结构模型修正领域，特别是一种结合随机变量灰性和贝叶斯模型修正的不确定性参数估计方法。

背景技术

结构健康监测中通常假定损伤会导致结构局部刚度发生变化，因此利用模型修正方法估计结构当前刚度参数是损伤识别的重要途径之一。近年来随着计算机技术的不断发展，模型修正技术^[1,2]在结构健康监测领域得到了不断发展和应用。传统的确定性模型修正技术难以考虑实际结构边界条件未知、材料离散性与观测噪声等不确定因素的影响，实用性不佳，使得考虑参数不确定性的模型修正方法逐渐受到重视。

当前不确定性参数识别方法主要基于贝叶斯模型修正、随机有限元模型修正和统计模式识别^[3]。相比于另外两种方法，贝叶斯模型修正能够充分利用结构的历史数据和当前实测数据信息，不断修正和更新待识别参数的先验概率分布，具备在线监测的独特优势^[4]。贝叶斯模型修正时通常将随机参数的先验和后验概率假定为某一常见分布如正态分布和均匀分布^[5-7]，然而实际工程中由于测试数据往往不充分，很多时候只能知道参数的大致取值范围，其概率分布形式不得而知，使得基于概率统计方法分析得到的参数后验概率分布估计值得商榷。因此，将结构随机参数考虑为存在一定取值范围的灰数，并将此类灰色随机变量纳入已有的贝叶斯模型修正过程更符合实际情况。

贝叶斯模型修正首先根据工程师的经验和历史数据大致估计结构随机参数的先验概率分布情况，然后在获取当前实测数据的基础上，通过贝叶斯公式不断修正更新先验分布，最终得到随机参数的后验概率分布估计。可见贝叶斯模型修正的本质是实现随机参数先验分布向后验分布的转化，但当前贝叶斯推断过程随机参数的选取是人为假定的(比如假定随机参数服从某一典型正态分布)，若真实分布与假定的不同，可能会得到错误的修正结果^[8]。从事物认知的角度来看，表征结构损伤的随机参数本质上可看作部分已知、部分未知的灰色量。一方面可以根据结构的工作状态大致推知损伤导致的随机参数变动范围，另一方面由于主观认知不足及实测数据欠缺，需要收集更多信息进一步判断参数值的大小(损伤程度)。这种对随机参数存在一定程度认识但又无法确知参数大小的情况与灰色系统的概念类似，同时贝叶斯模型修正过程与灰色系统的白化过程也有相似之处。因此，将结构随机参数认为是灰性的，即将灰色随机变量与贝叶斯模型修正相结合，能更加客观地反映实际工程结构随机参数的演化情况。

其中参考文献如下：

[1]m.i.friswell,j.e.mottershead,finiteelementmodelupdatinginstructuraldynamics[m].kluweracademicpress,dordrecht,1995。

[2]吴晓菊.结构有限元模型修正综述[j].《特种结构》,2009,26(1):39-45。

[3]宗周红,牛杰,王浩.基于模型确认的结构概率损伤识别方法研究进展[j].《土木工程学报》,2012(8):121-130。

[4]r.rocchetta,m.broggi,q.huchet,etal.on-linebayesianmodelupdatingforstructuralhealthmonitoring.mechanicalsystems&signalprocessing,2018,103:174-195。

[5]j.l.beck,l.s.katafygiotis.updatingmodelsandtheiruncertainties.i:bayesianstatisticalframework:journalofengineeringmechanics:(asce).journalofengineeringmechanics,1998,124(4):455-461。

[6]l.s.katafygiotis,j.l.beck.updatingmodelsandtheiruncertainties.ii:modelidentifiability.journalofengineeringmechanics,1998,124(4):463-467。

[7]颜王吉,曹诗泽,任伟新.结构系统识别不确定性分析的bayes方法及其进展[j].《应用数学和力学》,2017,38(1):44-59。

[8]张建新.基于贝叶斯方法的有限元模型修正研究[d].重庆大学,2014。

技术实现要素：

有鉴于此，本发明的目的是提出一种结合随机变量灰性和贝叶斯模型修正的不确定性参数估计方法，能够有效提高随机参数的估计精度。

本发明采用以下方案实现：一种结合随机变量灰性和贝叶斯模型修正的不确定性参数估计方法，具体包括以下步骤：

步骤s1：将结构随机参数表示为连续区间灰数，并求得该区间灰数的核与扩散度；

步骤s2：基于区间灰数的核与扩散度构造随机参数的灰色先验分布，不断进行样本抽取与判别，获得初始灰色区间随机样本集；

步骤s3：对步骤s2获得的样本集进行不断扰动和更新，并将所得样本的上下界置为更新后的区间灰数上下界；当区间宽度小于预设值时，终止迭代，以该区间灰数作为结构不确定性参数修正和估计的依据。

其中本发明采用群体蒙特卡洛抽样生成所需的参数样本。

本发明在贝叶斯模型修正方法中引入灰色随机变量，在假定结构随机参数为区间灰数的基础上，以其真实值服从正态分布作为补充信息，然后基于群体蒙特卡洛抽样完成灰色随机参数的后验概率分布估计。该发明首先在贝叶斯模型修正框架内考虑随机参数的灰色性质，然后从参数取值分布随机性的角度考虑区间灰数的特点，使用正态分布随机函数完成区间灰数的数值覆盖。与传统贝叶斯模型修正方法所采用的马尔科夫链蒙特卡洛抽样不同，本发明采用群体蒙特卡洛抽样生成所需的参数样本，然后估计参数的灰色区间，能够有效提高随机参数的估计精度。

本发明结构随机参数的区间灰数表示；使用正态分布随机函数完成区间灰数的数值覆盖，将区间灰数转化为等效的实数集合；运用群体蒙特卡洛抽样生成所需的参数样本，最终实现参数灰色区间估计。具体阐述如下：

对于结构随机参数θ，给定命题p，p(x)表示命题信息。在无法确知命题真实取值的情况下，可以给定该命题的可能取值区间i。若θ在区间i内的取值连续，那么命题p可理解为p(x)意义下的连续型灰数这里命题信息p(x)表示灰数在x处取值的可能性。令参数在该命题下的真值为x⁰，可见灰数描述了一个含有命题真值x⁰的数值区间i，而且的灰色程度(即不确定程度)依赖于命题信息p(x)。

若θ取值区间其中记连续型区间灰数为若参数真值x⁰的取值可能性p(x)服从正态分布，则称p为正态分布区间灰数，简记为本发明讨论的均为正态分布区间灰数。

基于正态分布的“3σ”原则定义区间灰数的核与信息扩散度。区间灰数的核：

区间灰数的信息扩散度：

于是有：基于上述假定，区间灰数真值x⁰的取值可能性服从正态分布那么x⁰落在内的概率为99.73％，基本实现了对灰数的数值覆盖。

由于区间灰数本身无法做一般概率统计意义下的处理，因此需要将其转化为信息等效的实数集合。由前述可知，使用蒙特卡洛抽样产生的随机样本有99.73％都将落在以为中心的3σ区间内，可以满足信息等效条件。另外，随机抽样获得的样本最大与最小值能够对应区间灰数的上下界信息，也满足了数据完整性原则。目前贝叶斯模型修正通常使用马尔科夫链蒙特卡洛抽样来完成参数收敛过程，但该方法存在陷入低概率区域抽样的风险，为此本发明采用群体蒙特卡洛抽样方法，对真值服从正态分布的区间灰数进行大量样本模拟，并将该过程与贝叶斯模型修正有机结合实现参数概率分布的更新。

进一步地，步骤s1具体包括以下步骤：

步骤s11：生成初始灰色区间随机样本集x1；

步骤s12：设结构随机参数θ的初始值为连续型区间灰数求得该区间灰数的核与扩散度：

式中，为区间灰数的核，σ0为区间灰数的扩散度。

进一步地，步骤s2具体包括以下步骤：

步骤s21：定义正态分布为参数初始概率分布π(θ)，从π(θ)中随机抽取一个参数样本将代入结构数值模型求得仿真样本

步骤s22：构造并计算仿真样本与实测样本d1之间的误差函数对于给定容差ε1，若则重新抽取否则保存该样本并进行下一个样本的抽取和判别，直到生成足够数目的参数样本。

进一步地，步骤s3具体包括以下步骤：

步骤s31：将参数样本的最小值a1和最大值置为更新后的区间灰数上下界，即并给所有样本设置相同的抽样权重w1＝1/n，其中n为样本数；计算当前迭代步t＝1时该样本集的方差样本方差定义为当前迭代步样本集方差的2倍：

步骤s32：后续迭代步t≥2时，对样本集xt中的样本进行扰动更新：从上一迭代步t-1的样本集xt-1里结合权重随机抽取样本并用上一迭代步t-1的样本集方差扰动使其成为具体操作上可以通过从中抽样来实现；

步骤s33：将代入结构数值模型求得仿真样本并判断仿真样本与实测样本之间的误差是否小于预设的容差，若是，保存该样本并计算其权重值，进入步骤s34，否则返回步骤s32；其中样本权重由当前样本的概率密度函数、上一迭代步得到的各样本的权重以及一个高斯概率转移核联合求得；

步骤s34：在样本集中所有样本都更新之后结束当前迭代步；每一步迭代之后计算样本集的方差，获得该迭代步内参数样本的上下界at和将其置换为更新后的区间灰数上下界，即

步骤s35：判断区间宽度是否小于预设的阈值，若是，则终止迭代，得到更新完毕的参数区间灰数否则，返回步骤s32。

考虑到实际结构边界条件未知、材料离散性与观测噪声等不确定性因素的影响，模型修正和参数估计过程中考虑参数的不确定性很有必要。传统的贝叶斯模型修正方法通常将随机参数的先验和后验概率假定为某一常见分布，然而由于实测数据的匮乏，很多时候只能知道参数的大致取值范围，想要基于统计数据获得参数的概率分布函数并不现实，那么基于概率统计方法分析得到的参数后验概率分布估计值得商榷。因此，在“少数据、贫信息”的情况下，将结构随机参数考虑为存在一定取值范围的灰数，并将此类灰色随机变量纳入已有的贝叶斯模型修正过程更符合实际情况。

与现有技术相比，本发明有以下有益效果：

1、将灰色随机变量纳入贝叶斯模型修正框架内，能够客观反映实际工程结构随机参数的灰色性质；

2、使用正态分布随机函数完成区间灰数的数值覆盖，实现了从灰数域向实数域的等信息转换；

3、基于群体蒙特卡洛抽样实现参数后验分布样本的生成并进行参数的灰色区间估计，相较于传统的马尔科夫链蒙特卡洛抽样能够有效提高随机参数的估计精度。

附图说明

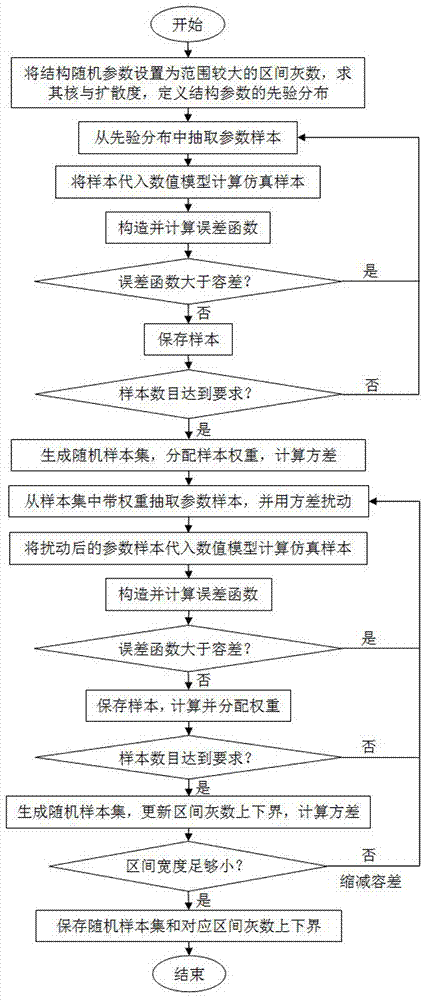
图1为本发明的方法流程示意图。

具体实施方式

下面结合附图及实施例对本发明做进一步说明。

应该指出，以下详细说明都是示例性的，旨在对本申请提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

如图1所示，本实施例提供了一种结合随机变量灰性和贝叶斯模型修正的不确定性参数估计方法，具体包括以下步骤：

步骤s1：将结构随机参数表示为连续区间灰数，并求得该区间灰数的核与扩散度；

步骤s2：基于区间灰数的核与扩散度构造随机参数的灰色先验分布，不断进行样本抽取与判别，获得初始灰色区间随机样本集；

步骤s3：对步骤s2获得的样本集进行不断扰动和更新，并将所得样本的上下界置为更新后的区间灰数上下界；当区间宽度小于预设值时，终止迭代，以该区间灰数作为结构不确定性参数修正和估计的依据。

其中本实施例采用群体蒙特卡洛抽样生成所需的参数样本。

本实施例在贝叶斯模型修正方法中引入灰色随机变量，在假定结构随机参数为区间灰数的基础上，以其真实值服从正态分布作为补充信息，然后基于群体蒙特卡洛抽样完成灰色随机参数的后验概率分布估计。该发明首先在贝叶斯模型修正框架内考虑随机参数的灰色性质，然后从参数取值分布随机性的角度考虑区间灰数的特点，使用正态分布随机函数完成区间灰数的数值覆盖。与传统贝叶斯模型修正方法所采用的马尔科夫链蒙特卡洛抽样不同，本发明采用群体蒙特卡洛抽样生成所需的参数样本，然后估计参数的灰色区间，能够有效提高随机参数的估计精度。

本实施例结构随机参数的区间灰数表示；使用正态分布随机函数完成区间灰数的数值覆盖，将区间灰数转化为等效的实数集合；运用群体蒙特卡洛抽样生成所需的参数样本，最终实现参数灰色区间估计。具体阐述如下：

对于结构随机参数θ，给定命题p，p(x)表示命题信息。在无法确知命题真实取值的情况下，可以给定该命题的可能取值区间i。若θ在区间i内的取值连续，那么命题p可理解为p(x)意义下的连续型灰数这里命题信息p(x)表示灰数在x处取值的可能性。令参数在该命题下的真值为x⁰，可见灰数描述了一个含有命题真值x⁰的数值区间i，而且的灰色程度(即不确定程度)依赖于命题信息p(x)。

若θ取值区间其中记连续型区间灰数为若参数真值x⁰的取值可能性p(x)服从正态分布，则称p为正态分布区间灰数，简记为本发明讨论的均为正态分布区间灰数。

基于正态分布的“3σ”原则定义区间灰数的核与信息扩散度。区间灰数的核：

区间灰数的信息扩散度：

于是有：基于上述假定，区间灰数真值x⁰的取值可能性服从正态分布那么x⁰落在内的概率为99.73％，基本实现了对灰数的数值覆盖。

由于区间灰数本身无法做一般概率统计意义下的处理，因此需要将其转化为信息等效的实数集合。由前述可知，使用蒙特卡洛抽样产生的随机样本有99.73％都将落在以为中心的3σ区间内，可以满足信息等效条件。另外，随机抽样获得的样本最大与最小值能够对应区间灰数的上下界信息，也满足了数据完整性原则。目前贝叶斯模型修正通常使用马尔科夫链蒙特卡洛抽样来完成参数收敛过程，但该方法存在陷入低概率区域抽样的风险，为此本发明采用群体蒙特卡洛抽样方法，对真值服从正态分布的区间灰数进行大量样本模拟，并将该过程与贝叶斯模型修正有机结合实现参数概率分布的更新。

在本实施例中，步骤s1具体包括以下步骤：

步骤s11：生成初始灰色区间随机样本集x1；

步骤s12：设结构随机参数θ的初始值为连续型区间灰数求得该区间灰数的核与扩散度：

式中，为区间灰数的核，σ0为区间灰数的扩散度。

在本实施例中，步骤s2具体包括以下步骤：

步骤s21：定义正态分布为参数初始概率分布π(θ)，从π(θ)中随机抽取一个参数样本将代入结构数值模型求得仿真样本

步骤s22：构造并计算仿真样本与实测样本d1之间的误差函数对于给定容差ε1，若则重新抽取否则保存该样本并进行下一个样本的抽取和判别，直到生成足够数目的参数样本。

在本实施例中，步骤s3具体包括以下步骤：

步骤s31：将参数样本的最小值a1和最大值置为更新后的区间灰数上下界，即并给所有样本设置相同的抽样权重w1＝1/n，其中n为样本数；计算当前迭代步t＝1时该样本集的方差样本方差定义为当前迭代步样本集方差的2倍：

步骤s32：后续迭代步t≥2时，对样本集xt中的样本进行扰动更新：从上一迭代步t-1的样本集xt-1里结合权重随机抽取样本并用上一迭代步t-1的样本集方差扰动使其成为具体操作上可以通过从中抽样来实现；

步骤s33：将代入结构数值模型求得仿真样本并判断仿真样本与实测样本之间的误差是否小于预设的容差，若是，保存该样本并计算其权重值，进入步骤s34，否则返回步骤s32；其中样本权重由当前样本的概率密度函数、上一迭代步得到的各样本的权重以及一个高斯概率转移核联合求得；

步骤s34：在样本集中所有样本都更新之后结束当前迭代步；每一步迭代之后计算样本集的方差，获得该迭代步内参数样本的上下界at和将其置换为更新后的区间灰数上下界，即

步骤s35：判断区间宽度是否小于预设的阈值，若是，则终止迭代，得到更新完毕的参数区间灰数否则，返回步骤s32。

考虑到实际结构边界条件未知、材料离散性与观测噪声等不确定性因素的影响，模型修正和参数估计过程中考虑参数的不确定性很有必要。传统的贝叶斯模型修正方法通常将随机参数的先验和后验概率假定为某一常见分布，然而由于实测数据的匮乏，很多时候只能知道参数的大致取值范围，想要基于统计数据获得参数的概率分布函数并不现实，那么基于概率统计方法分析得到的参数后验概率分布估计值得商榷。因此，在“少数据、贫信息”的情况下，将结构随机参数考虑为存在一定取值范围的灰数，并将此类灰色随机变量纳入已有的贝叶斯模型修正过程更符合实际情况。

以上所述仅为本发明的较佳实施例，凡依本发明申请专利范围所做的均等变化与修饰，皆应属本发明的涵盖范围。