一种基于部分奇异值和的磁共振波谱重建方法与流程

本发明涉及磁共振波谱重建方法，尤其是涉及一种基于部分奇异值和的磁共振波谱重建方法。

背景技术：

在生物医学应用中，磁共振波谱可以确定几乎所有常见官能团的环境，是生物医学工程中进行机构分析的强有力手段之一。在实际运用中，由于磁共振采样时间较长，为了节省采样时间，可以磁共振波谱的时间信号进行欠采样并进行时间信号或者对应频谱的欠采样重建。基于低秩汉克尔矩阵的方法(x.qu,m.mayzel,j.-f.cai,z.chen,andv.orekhov,“acceleratednmrspectroscopywithlow-rankreconstruction,”angewandtechemieinternationaledition,2015，54(3)：852-854；j.ying,h.lu,q.wei,j.-f.cai,d.guo,j.wu,z.chen,andx.qu,“hankelmatrixnuclearnormregularizedtensorcompletionforn-dimensionalexponentialsignals,”ieeetransactionsonsignalprocessing,2017，65(14)：3702-3717；h.lu,x.zhang,t.qiu,j.yang,j.ying,d.guo,z.chen,andx.qu,“lowrankenhancedmatrixrecoveryofhybridtimeandfrequencydatainfastmagneticresonancespectroscopy,”ieeetransactionsonbiomedicalengineering,2018，65(4)：809-820；d.guo,h.lu,andx.qu,“afastlowrankhankelmatrixfactorizationreconstructionmethodfornon-uniformlysampledmagneticresonancespectroscopy,”ieeeaccess,2017，5,16033-16039；d.guo,andx.qu,“improvedreconstructionoflowintensitymagneticresonancespectroscopywithweightedlowrankhankelmatrixcompletion,”ieeeaccess,2018，6，4933-4940)提供了很好的重建结果。但在采样率较低时，这些重建方法可能无法可靠地重建低强度峰。

技术实现要素：

本发明的目的在于提供重建精度高，尤其在低强度峰值重建方面效果较好的一种基于部分奇异值和的磁共振波谱重建方法。

本发明包括以下步骤：

1)构建汉克尔矩阵；

在步骤1)中，所述构建汉克尔矩阵的具体方法可为：给定一个维度为n的复数向量其形式为x＝[x1,x2,x3,…,xn]^t，其中，上标t表示对向量进行转置，将x转为汉克尔矩阵的算子记为满足如下形式：

其中，q是表示汉克尔矩阵的列数。

2)建立基于部分奇异值和的汉克尔矩阵重建模型：

其中，x为待重建的磁共振波谱的时间信号，表示对x进行欠采样，y为欠采样得到的时间信号，λ为正则化参数并用于权衡和的重要性，||·||p＝r表示矩阵的部分奇异值和(t.h.oh,y.w.tai,j.c.bazin,h.kim,andi.s.kweon,“partialsumminimizationofsingularvaluesinrobustpca:algorithmandapplications,”ieeetransactionsonpatternanalysisandmachineintelligence,2016，38(4)：744-758,)，下标p＝r表示的是部分奇异值和当中预设的矩阵秩为r，一般取正整数。部分奇异值和的定义式为：

其中，min(n-q+1,q)为n-q+1与q中的最小值，σi(x)为矩阵x的第i大的奇异值；

3)基于部分奇异值和的汉克尔矩阵重建模型的求解算法；

在步骤3)中，所述基于部分奇异值和的汉克尔矩阵重建模型的求解算法的具体方法可为：为求解(2)中的重建模型，采用交替乘子算法(x.qu,m.mayzel,j.-f.cai,z.chen,andv.orekhov,“acceleratednmrspectroscopywithlow-rankreconstruction,”angewandtechemieinternationaledition,vol.54,no.3,pp.852-4,2015)，引入一个中间变量z，令将式(2)松弛为：

式(4)的增广拉格朗日形式为：

其中，＜·,·＞为向量内积空间，即表示取复数的实部，表示矩阵的弗罗贝尼乌斯范数的平方，参数β取大于零的值，d为拉格朗日乘子；

采用交替乘子法对式(5)求解，式(5)的优化问题可以通过求解下式得到：

对x进行求解，结果为：

其中，x^k+1为x第k+1次迭代时的值，z^k,d^k为z,d第k次迭代时的值，*表示共轭算子，矩阵右上角符号“-1”表示矩阵的逆。

采用部分奇异值收缩算子(t.h.oh,y.w.tai,j.c.bazin,h.kim,andi.s.kweon,“partialsumminimizationofsingularvaluesinrobustpca:algorithmandapplications,”ieeetransactionsonpatternanalysisandmachineintelligence,vol.38,no.4,pp.744-758,2016.)对z进行求解，结果为：

其中，z^k+1为z第k+1次迭代时的值，为部分奇异值收缩算子。令部分奇异值收缩算子的定义为：

其中，

dy1＝diag(σ1,...,σr,0,...,0)(10)

dy2＝diag(0,...,0,σr+1,...,σmin(n-q+1,q))(11)

其中，diag(·)表示将向量对角化成矩阵，也就是将括号中的元素依次替换一个全零矩阵的对角元素；

令g表示dy2对角线上的元素，为软阈值算子，sign(g)表示变量g的符号函数，表示取与0当中的最大值；

最后，对d求解，结果为：

d^k+1←d^k+τ(rx^k+1-z^k+1)(12)

其中，τ为迭代步长；

当达到迭代停止准则时，可根据公式(7)得到完整的x^k+1，即为磁共振波谱的完整时间信号。迭代停止准则设定为小于设置的阈值η或达到最大迭代次数。

4)对x^k+1进行傅里叶变换得到磁共振波谱。

本发明从磁共振波谱的时间信号特性出发，采用基于部分奇异值和的方法来更好地重建低强度谱峰。首先引入汉克尔矩阵，然后提出基于部分奇异值和的信号重建模型，之后采用迭代算法求解得到补全的磁共振波谱的时间信号，最后对补全的时间信号进行傅里叶变换得到磁共振波谱。该方法能较准确地重建低强度谱峰。

附图说明

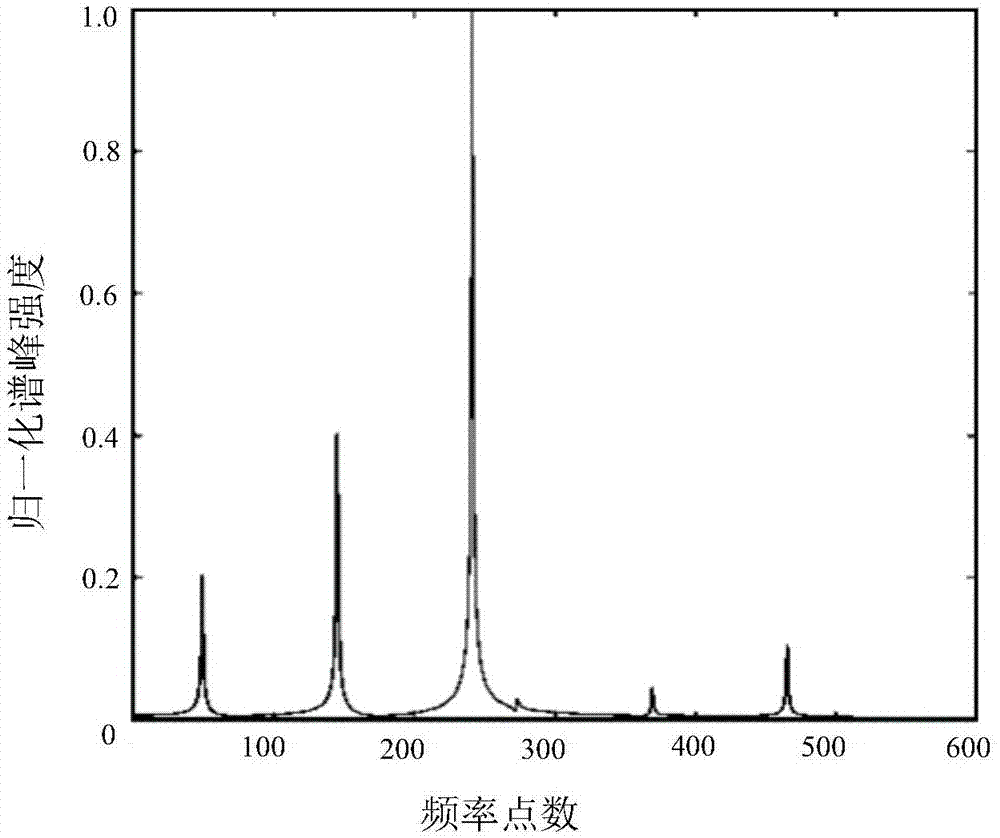
图1为全采样512个数据点的磁共振波谱。

图2为本发明用欠采样后的41个数据点重建得到的磁共振波谱。

具体实施方式

下面通过具体实施例对本发明作进一步的说明，并给出重建结果。使用一维磁共振波谱的时间域的全采样的512个数据点，经过傅里叶变换得到的完整磁共振波谱(如图1所示)。对512个数据进行欠采样，采样率为8％，得到的总采样数据点为41个。利用部分奇异值和的汉克尔矩阵重建得到的磁共振波谱(如图2所示)。

本发明包括以下步骤：

1)构建汉克尔矩阵：给定一个维度为n的复数向量其形式为x＝[x1,x2,x3,…,xn]^t，其中的上标t表示对向量进行转置，记将x转为汉克尔矩阵的算子为满足如下形式:

其中，q是表示汉克尔矩阵的列数。此处，n＝512，q＝256。

2)建立基于部分奇异值和的汉克尔矩阵重建模型：

其中，x为待重建的磁共振波谱的时间信号，表示对x进行欠采样，y为欠采样得到的时间信号，λ为正则化参数并用于权衡和的重要性。||·||p＝r表示矩阵的部分奇异值和(t.h.oh,y.w.tai,j.c.bazin,h.kim,andi.s.kweon,“partialsumminimizationofsingularvaluesinrobustpca:algorithmandapplications,”ieeetransactionsonpatternanalysisandmachineintelligence,vol.38,no.4,pp.744-758,2016.)，下标p＝r表示的是部分奇异值和当中预设的矩阵秩为r，一般取正整数。此处，p＝r＝5，λ＝500。部分奇异值和的定义式为：

其中，min(n-q+1,q)为n-q+1与q中的最小值，σi(x)为矩阵x的第i大的奇异值。

1)基于部分奇异值和的汉克尔矩阵重建模型的求解算法：为求解(2)中的重建模型，采用交替乘子算法(x.qu,m.mayzel,j.-f.cai,z.chen,andv.orekhov,“acceleratednmrspectroscopywithlow-rankreconstruction,”angewandtechemieinternationaledition,vol.54,no.3,pp.852-4,2015.)，引入一个中间变量z，令将式(2)松弛为：

式(4)的增广拉格朗日形式为：

其中，＜·,·＞为向量内积空间，即表示取复数的实部。表示矩阵的弗罗贝尼乌斯范数的平方，参数β取大于零的值，d为拉格朗日乘子。此处，β＝1。

采用交替乘子法对式(5)求解，式(5)的优化问题可以通过求解下式得到：

对x进行求解，结果为：

其中，x^k+1为x第k+1次迭代时的值，z^k,d^k为z,d第k次迭代时的值，*表示共轭算子，矩阵右上角符号“-1”表示矩阵的逆。

采用部分奇异值收缩算子(t.h.oh,y.w.tai,j.c.bazin,h.kim,andi.s.kweon,“partialsumminimizationofsingularvaluesinrobustpca:algorithmandapplications,”ieeetransactionsonpatternanalysisandmachineintelligence,vol.38,no.4,pp.744-758,2016.)对z进行求解，结果为：

其中，z^k+1为z第k+1次迭代时的值，为部分奇异值收缩算子。令部分奇异值收缩算子的定义为：

其中，

dy1＝diag(σ1,...,σr,0,...,0)(10)

dy2＝diag(0,...,0,σr+1,...,σmin(n-q+1,q))(11)

其中，diag(·)表示将向量对角化成矩阵，也就是将括号中的元素依次替换一个全零矩阵的对角元素。令g表示dy2对角线上的元素，为软阈值算子，sign(g)表示变量g的符号函数，表示取与0当中的最大值。

最后，对d求解，结果为：

d^k+1←d^k+τ(rx^k+1-z^k+1)(12)

其中，τ为迭代步长，此处τ＝1。

当达到迭代停止准则时，可根据公式(7)得到完整的x^k+1，即为磁共振波谱的完整时间信号。迭代停止准则设定为小于设置的阈值η＝10^-4，或达到最大迭代次数200次。

2)对x^k+1进行傅里叶变换得到磁共振波谱。