一种基于贝叶斯结构学习的航班保障Petri网构建方法及系统与流程

本发明属于民航航空技术领域，具体涉及一种基于贝叶斯结构学习的航班保障petri网构建方法及系统。

背景技术：

近几年民航运输业高速发展，截止2017年旅客吞吐量达千万级机场已有32个，以2月份全球机场放行准点率数据为例，其中国内放行准点率最高机场为大连国际机场，准点率80.89％，相比于日本伊丹机场95.13％的放行准点率有较大差距。造成放行准点率低的主要原因之一是地面服务保障低效。目前中国民航局力推建设机场协同决策支持系统a-cdm有望解决此难题。其中a-cdm通过获得精确的撤轮档时间将有助于提高地面服务保障的效率，实现机场与空管、航空公司共同规划合理的航班放行顺序，从而提升航班正常放行率。因此，机场航班保障高效运行迫切需要精细刻画服务保障过程来获得精准的撤轮档预测时间。

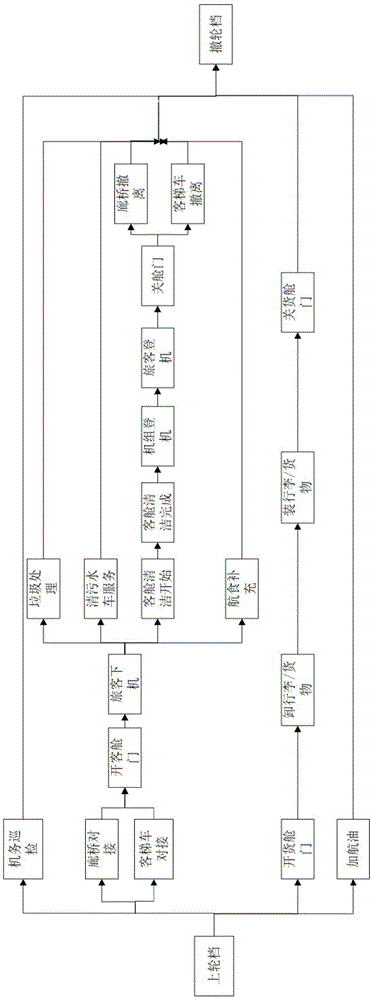
过站航班地面服务，从上轮档到撤轮档的过程中一共包含20个业务环节。按照各业务环节的依赖关系将上轮档到撤轮档之间的业务环节分为机务巡检、客舱服务、货舱服务以及加航油四个并行的业务流程。各服务流程包含子环节，完整的航班计划保障服务工作流程如图1所示。上述保障流程是按照业务环节的先后顺序得到的计划执行过程，在实际保障过程中高峰时段因机场保障资源有限，航班保障服务的各业务环节的执行顺序会发生变化，导致航班计划保障流程不能正确的刻画实际的航班保障过程。

在航班保障流程中，机务巡检和加航油的时间窗口较大，而且不影响客舱和货舱服务流程。客舱服务流程中，首先要进行廊桥对接，之后进行开客舱门和旅客下机。本发明将开客舱门和旅客下机视为同一环节。在完成此环节之后，在并行开展的四个环节中，只有客舱清洁开始和完成在客舱内部进行，并且影响之后的保障环节。货舱服务流程中，开货舱门完成后，其他的保障环节才能依次进行。所以，确定上轮档、廊桥对接、开货舱门、开客舱门、客舱清洁开始和完成保障环节的网络结构关系就显得尤为重要。

综上所述，在航班保障流程中，本发明将上轮档、廊桥对接、开货舱门、开客舱门、客舱清洁开始及完成这六个保障环节定义为关键节点。其余保障环节在满足串行关系和并行关系的业务前提下，网络结构会随着六个环节的确定而确定。此六项环节的网络结构将直接决定航班保障流程的网络结构。为准确预测撤轮档时间，必须预测保障过程中各关键节点的时间。

技术实现要素：

本发明提供了一种基于贝叶斯结构学习的航班保障petri网构建方法及系统相比于航班保障计划流程关键点petri网，本发明结合先验节点顺序、历史数据以及最大节点个数，通过k2算法构建的航班保障关键点petri网，预测的结果更准确，更能准确反映航班保障关键节点的真实过程。

此外，本发明没有按照多数情况下，利用petri网的变迁表示业务环节的方法，而是采用库所表示航班保障的业务环节。原因是前者虽然便于理解，但是将造成加入时间因素后，系统的状态无法用可达图表示的情况。因此，为保证后续研究的一致性，本发明采用库所表示业务环节的方法。

第一方面，本发明提供了一种基于贝叶斯结构学习的航班保障petri网构建方法，包括以下步骤:

根据贝叶斯网络的无自环petri网描述航班保障计划流程，并得到航班保障计划流程关键点petri网和先验节点顺序ρ；

对航班历史数据进行数据处理得到矩阵形式的历史数据集d；

基于先验节点顺序ρ、历史数据集d以及设置的最大父节点个数，通过贝叶斯结构学习k2算法的计算，得到更能体现航班真实流程的航班保障关键点petri网。

优选地，所述贝叶斯结构学习k2算法具体为：

根据历史数据集d计算每个节点的初始评分；

根据先验节点顺序ρ、历史数据集d以及最大父节点个数u，通过ch评分函数计算每个节点的结构评分，并将结构评分与初始评分进行比较，最终确定每个节点的父节点；

确定每个节点的父节点后，得到基于贝叶斯结构学习的航班保障关键点petri网。

优选地，所述ch评分函数为：

其中，d为历史数据集；

i表示第i个节点，1≤i≤n，n为节点总数；

si表示第i个节点对应的库所；

π(si)表示第i个节点对应的父库所；

ch(〈si,π(si)>|d)表示第i个节点的结构评分；

mijk表示历史数据集d中，在父库所π(si)取值组合编号为j的条件下，节点i取值为k的样本数量；

mij*表示样本中i节点在父库所取值组合编号为j时的样本总量；

k表示库所si的取值，1≤k≤ri，ri是所有库所si取值状态的最大值；

j表示父库所π(si)取值组合的编号，1≤j≤qi，qi是父库所π(si)取值组合的最大值，即最大取值为样本总量m。

优选地，所述的基于贝叶斯结构学习的航班保障petri网构建方法，还包括：

从时间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析的步骤。

优选地，所述的基于贝叶斯结构学习的航班保障petri网构建方法，还包括：

从空间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析的步骤。

优选地，所述的基于贝叶斯结构学习的航班保障petri网构建方法，还包括：

从结构评分对航班保障计划流程关键点petri网和航班保障关键点petri网进行分析的步骤。

第二方面，本发明提供了一种基于贝叶斯结构学习的航班保障petri网构建系统，适用于第一方面所述的基于贝叶斯结构学习的航班保障petri网构建方法，包括：

计划网络单元，用于根据贝叶斯网络的无自环petri网描述航班保障计划流程，并得到航班保障计划流程关键点petri网和先验节点顺序ρ；

数据处理单元，用于对航班历史数据进行数据处理得到矩阵形式的历史数据集d；

计算网络单元，用于基于先验节点顺序ρ、历史数据集d以及设置的最大父节点个数，通过贝叶斯结构学习k2算法的计算，得到更能体现航班真实流程的航班保障关键点petri网。

本发明的有益效果为：相比于航班保障计划流程关键点petri网，本发明结合先验节点顺序、历史数据以及最大节点个数，通过k2算法构建的航班保障关键点petri网，预测的结果更准确，更能准确反映航班保障关键节点的真实过程。

附图说明

为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍。在所有附图中，所述的单元或步骤仅仅是一种逻辑性的划分，也可以有其他的划分方式。

图1为背景技术中航班计划保障服务工作流程图；

图2为本实施例中基于贝叶斯结构学习的航班保障petri网构建方法的流程图；

图3为本实施例中航班保障计划流程关键点petri网的示意图；

图4为本实施例中基于贝叶斯结构学习的航班保障关键点petri网的网络结构；

图5为本实施例中基于贝叶斯结构学习的航班保障关键点petri网的示意图；

图6为本实施例中基于贝叶斯结构学习的航班保障petri网构建系统的结构框图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

应当理解，在本发明说明书和所附权利要求书中，术语“包括”和“包含”指示所描述特征、整体、步骤、操作、元素和/或组件的存在，但并不排除一个或多个其它特征、整体、步骤、操作、元素、组件和/或其集合的存在或添加。

还应当理解，在本发明说明书和所附权利要求书中所使用的术语仅仅是出于描述特定实施例的目的而并不意在限制本发明。如在本发明说明书和所附权利要求书中所使用的那样，除非上下文清楚地指明其它情况，否则单数形式的“一”、“一个”及“该”意在包括复数形式。

还应当进一步理解，在本发明说明书和所附权利要求书中使用的术语“和/或”是指相关联列出的项中的一个或多个的任何组合以及所有可能组合，并且包括这些组合。

本实施例提供了一种基于贝叶斯结构学习的航班保障petri网构建方法，如图2所示，包括但不限于以下步骤:

s1，根据贝叶斯网络的无自环petri网描述航班保障计划流程，并得到航班保障计划流程关键点petri网和先验节点顺序ρ；

s2，对航班历史数据进行数据处理得到矩阵形式的历史数据集d；

s3，基于先验节点顺序ρ、历史数据集d以及设置的最大父节点个数，通过贝叶斯结构学习k2算法的计算，得到更能体现航班真实流程的航班保障关键点petri网。

本实施例中，贝叶斯网络用一个有向无环图描述了节点(也称作变量)之间的依赖关系，如果节点x到节点y有一条边，那么称x为y的父节点，而y为x的子节点，将父节点视作原因，子节点视作结果，贝叶斯网络是从原因到结果的推理过程。petri网中s表示库所，代表实物的状态。实物标识由一个库所传入下一个库所，可以看作实物由状态1切换到状态2，利用贝叶斯网络可以将前一个库所代表的状态视为父状态，后者为子状态。在航班保障流程中，实物代表需要进行航班保障的航班，上轮档到撤轮档的业务流程看作由父状态到子状态的发生过程。每个业务环节的发生都以父状态的发生为前提，例如上轮档环节发生导致廊桥对接、机务巡检、开货舱门、加航油发生，开货舱门业务环节完成才能进行装卸货物的业务操作。因此，从上轮档到撤轮档的过程，可以利用一种基于贝叶斯的petri网进行描述。

由以上论述及贝叶斯是无环图的设定，定义一种基于贝叶斯网络的无自环petri网，用于描述航班保障计划流程。

定义1：∑＝(s，t，f)为一个petri网，并且si∈s表示节点变量，若si∈·tk且sj∈tk·，则si为sj的父库所，记为si＝π(sj)，称∑为贝叶斯无自环petri网。

利用上述定义描述的网络，得到航班保障计划流程关键点petri网，如图3所示，以及先验节点顺序ρ＝{1，3，2，4，5，6}。

图3中，库所与保障环节对应关系如表1所示。

表1库所与保障环节对应关系

根据定义1知，s1＝π(s2)，s1＝π(s3)，s2＝π(s4)，s4＝π(s5)，s5＝π(s6)，对应航班保障流程因果关系为上轮档是廊桥对接和开货舱门的父状态。廊桥对接完成导致开客舱门环节发生，后者为前者的子状态。开客舱门完成并且旅客下机结束才能进行客舱清洁环节，后者同样为前者的子状态。所有的子状态只有在父状态完成的情况下才能进行，这也符合航班保障业务环节的先后顺序。

本实施例中，所述历史数据包括上述六个保障关键环节的历史数据，利用k-mean聚类算法对各环节的时间数据聚类，将聚类后的数据处理为矩阵形式，从而得到历史数据集d。

本实施例中，所述贝叶斯结构学习k2算法具体为：

s31，根据历史数据集d计算每个节点的初始评分；

s32，根据先验节点顺序ρ、历史数据集d以及最大父节点个数u，通过ch评分函数计算每个节点的结构评分，并将结构评分与初始评分进行比较，最终确定每个节点的父节点；

s33，确定每个节点的父节点后，得到基于贝叶斯结构学习的航班保障关键节点网络。

本实施例中，图3的航班保障计划流程关键点petri网，是基于业务环节的先后顺序的计划流程，其计划网络对各环节的时间预测有一定偏差，真实情况的网络结构要从历史数据中确定，才能还原航班保障关键节点的网络结构。本实施例选择贝叶斯结构学习k2算法从历史数据中确定真实情况的关键节点的网络结构。

贝叶斯网络中的k2算法是最早的贝叶斯结构学习算法之一，算法的目的是在已知先验节点顺序ρ和最大父节点个数u(u根据需要设置)的前提下，寻找ch评分函数最高的网络结构，ch评分是基于节点变量、其父节点以及它们之间的边形成的局部结构的评分函数。

在航班保障流程中，以库所si及父库所π(si)分别作为节点变量及其父节点，从而得到基于父子库所的航班保障关键节点k2算法的ch评分函数：

其中，d＝(d1,d2,…,dn)为历史数据集，n为节点总数，di∈d；

i表示第i个节点，1≤i≤n；

si表示第i个节点对应的库所；

π(si)表示第i个节点对应的父库所；

ch(<si,π(si)>|d)表示第i个节点的结构评分；

mijk表示历史数据集d中，在父库所π(si)取值组合编号为j的条件下，节点i取值为k的样本数量；

mij*表示样本中i节点在父库所取值组合编号为j时的样本总量；

k表示库所si的取值，1≤k≤ri，ri是所有库所si取值状态的最大值；

j表示父库所π(si)取值组合的编号，1≤j≤qi，qi是父库所π(si)取值组合的最大值，即最大取值为样本总量m。

本实施例中共有六个关键节点，先计算每个节点的初始评分。本实施例设置最大父节点个数为u，即将本节点之间的u个节点作为准父节点，通过ch评分函数的计算，从这u个节点中选择出本节点的父节点。例如，若u为2,则有两个准父节点，将本节点之前的节点q选为准父节点，并计算此时本节点的结构评分，若结构评分小于初始评分，则不是本节点的父节点；再将本节点之前的节点p选为父节点，并计算此时本节点的结构评分，若结构评分大于初始评分，则确定节点p为本节点的父节点。得到所有节点的网络结构，从而得到基于贝叶斯结构学习的航班保障关键点petri网，如图5所示。

本实施例中，算法：k2(s,ρ,u,d)。

输入：s＝(s1,s2,…,s6)为库所变量；ρ为先验节点顺序；u为最大父节点个数；d为历史数据集。

输出：航班保障关键点计算网络。

基于父子库所的航班保障关键节点k2算法伪代码流程图如下：

1，g←s1,s2,…,s6组成的无边图；

2，fori＝1ton；

3，π(si)←φ；

4，vold←ch(<si,π(si)>|d)；

5，while(true)；

6，

7，vnew←ch(<si,π(si)∪{sj}>|d)

8，if(vnew>voldand|π(si)|<u)；

9，vold←vnew；

10，π(si)←π(si)∪{sj}；

11，在g中添加边sj→si；

12，else

13，break；

14，endif

15，endwhile

16，endfor

17，return(g)。

综上所述，本实施例的方法，结合先验节点顺序、历史数据以及最大父节点个数，通过k2算法构建的航班保障关键点petri网，相比于航班保障计划流程关键点petri网，更能准确反映航班保障关键节点的真实过程。

下面从时间复杂度、空间复杂度和和结构评分分析本实施例技术方案的优越性。

一、航班保障关键节点k2算法时间复杂度分析

本实施例中，基于贝叶斯结构学习的航班保障petri网构建方法，还包括：从时间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析的步骤，从分析中得到k2算法相对于贪心算法降低了时间复杂度。

在流程图中，假设计算公式(1)需要的阶乘结果已经储存在计算机中，那么第四行ch评分函数的时间复杂度为o(mr)，第六行在第四行的基础上最多计算n次最大值，所以时间复杂度为o(mnr)，if循环的最多执行u次，所以while循环的时间复杂度为o(mnur)。for循环需要执行n次，因此关键节点k2算法的时间复杂度为o(mn²ur)。而现应用的贪心算法时间复杂度为o(mn²r2ⁿ)。存在如下性质：

性质1：假设m为样本数量，n为航班保障关键节点数，u表示最大父节点个数，r是节点取值状态的最大值，满足m,n,r,u∈n⁺,1≤u<n，那么mn²r2ⁿ>mn²ur。

证明：要证mn²r2ⁿ>mn²ur，即证2ⁿ>u，说明样本数量和取值状态不影响两者大小的比较。因为n,u∈n⁺,1≤u<n，所以2ⁿ>u，即mn²r2ⁿ>mn²ur。证毕

性质1说明k2算法计算局部父子节点评分的方法将指数级的时间复杂度降低为多项式时间复杂度，因此本方法的k2算法相对于贪心算法降低了时间复杂度。

二、航班保障关键节点k2算法空间复杂度分析

本实施例中，基于贝叶斯结构学习的航班保障petri网构建方法，还包括：从空间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析的步骤，从分析中得到k2算法相对于贪心算法降低了空间复杂度。

贝叶斯网络结构的搜索空间为这是利用贪心算法在全局范围内搜索最优网络的结构学习算法的可行域。在某一特定排序下，航班保障关键节点的搜索空间为同样存在如下性质：

性质2：n为网络节点数，满足n∈n⁺，那么f(0)＝＝f(1)。

证明：令要证命题成立，即证g(n)≥0。

采用数学归纳法

当n＝2时，

假设n＝k，成立

当n＝k+1时，

将代入上式中的第一项，将含有f(0)、f(1)、…、f(n-1)、f(n)的项合并，得到下式

又k+2≥k+1-i，i≥1则

即n＝k+1时，命题成立，则原不等式成立。证毕

性质2说明，加入节点排序缩小了贝叶斯网络结构的可行域。代入数值验证，在含有六个节点的贝叶斯网络中，贪心算法的搜索空间为k2算法的搜索空间仅为可以从数值上直观的看出加入节点排序，本方法的k2算法相对于贪心算法极大的缩小了空间复杂度。

三、航班保障关键节点k2算法结构评分分析

本实施例中，基于贝叶斯结构学习的航班保障petri网构建方法，还包括：从结构评分对航班保障计划流程关键点petri网和航班保障关键点petri网进行分析的步骤，从分析中得到航班保障关键点计算网络更准确，更能体现航班真实流程。

本实施例使用国内某枢纽机场的航班保障数据，选取早高峰时段的3u8741航班上轮档、廊桥对接、开货舱门、开客舱门、清洁开始、清洁结束，六个保障关键环节的数据进行实验，利用k-mean聚类算法对各环节的时间数据聚类，具体结果见表2、3。

表2前三个环节聚类时间及类别

表3后三个环节聚类时间及类别

将每个聚类时刻的类别作为各变量的状态取值，即本实施例中六个保障环节依次有11、10、9、10、11、13个取值状态。再将数据处理为矩阵形式，其中行代表六个保障环节，每一列就是完整的各环节的数据。先验的节点排序为ρ＝{1，3，2，4，5，6}，节点序号依次代表上轮档、廊桥对接、开货舱门、开客舱门、清洁开始、清洁结束。设最大父节点个数u为3。将历史数据d、节点排序ρ和节点最大父所库个数u输入航班保障关键节点k2算法，算法通过ch评分输出六个保障环节的网络结构，如图4所示。

图4中，存在父子库所结构的各保障环节ch评分结果见表4。

表4ch函数评分结果

利用定义1刻画六个保障环节关键节点，得到更能体现航班真实流程的航班保障关键点petri网，如图5所示。

对比图3的航班保障计划流程关键点petri网，可知开客舱门在廊桥对接之后,而从数据中确定的保障流程，即基于贝叶斯结构学习的航班保障关键点petri网，可知两者是并行关系。图5中，s4与s1组成的结构评分为ch(<s4,s1)>|d)＝-124.4010。而图3中，按照计划保障流程，廊桥对接和开客舱门组成的结构评分为ch(<s4,s2)>|d)＝-186.7176。

在同一时间区间内，随机选取不同时段的三个过站航班。cz330航班在下午进行航班保障，3u8205的保障任务在晚上执行，9c8563为凌晨到达该机场的过站航班。同样将三个航班的关键节点数据处理为矩阵形式输入航班保障关键节点k2算法，均得到图5的实验结果。其中，上轮档及开客舱门的局部评分与计划保障流程局部结构的评分结果如表5所示。

表5不同航班号对应两种网络结构的ch评分

在实验数据可知，开客舱门与上轮档构成父子状态的局部网络结构评分高于计划保障流程的评分。说明在实际的航班保障流程中，记录的廊桥对接时间为此环节完成的时间，而开客舱门环节在此之后立即执行。因此在历史数据方面，两者记录的时刻几乎相同，通过贝叶斯结构学习得到两个环节并行的网络结构，如图5所示。在客舱服务流程中，如果利用计划流程作为实际的网络结构预测各保障环节的开始和执行时间，那么后续环节会将廊桥对接时间纳入统计时间内，造成串行环节时间预测的偏差。实验结果证明基于历史数据确定航班保障流程网络结构的方法，而得到的航班保障关键点petri网，更能反映真实情况。

本实施例基于航班保障的历史数据，对航班保障流程的关键节点网络进行探究，结果表明：

1)基于贝叶斯结构学习k2算法得到航班保障关键点petri网的方法可行，能够真实反映航班保障关键节点的真实过程。

2)以历史数据得到保障环节关键节点网络结构，并以此作为预测各保障环节的结构基础，能得到更准确的预测结果。

3)利用贝叶斯网络结构学习的方法，为通过参数学习得到各环节的开始时间，从而精确预测撤轮档时间提供了前期的预备性研究。

实施例二：

本实施例提供了一种基于贝叶斯结构学习的航班保障petri网构建系统，适用于实施例一所述的基于贝叶斯结构学习的航班保障petri网构建方法，如图6所示，包括但不限于如下单元：计划网络单元、数据处理单元和计算网络单元。

计划网络单元，用于根据贝叶斯网络的无自环petri网描述航班保障计划流程，并得到航班保障计划流程关键点petri网和先验节点顺序ρ；

数据处理单元，用于对航班历史数据进行数据处理得到矩阵形式的历史数据集d；

计算网络单元，用于基于先验节点顺序ρ、历史数据集d以及设置的最大父节点个数，通过贝叶斯结构学习k2算法的计算，得到更能体现航班真实流程的航班保障关键点petri网。

其中，所述贝叶斯结构学习k2算法具体为：

根据历史数据集d计算每个节点的初始评分；

根据先验节点顺序ρ、历史数据集d以及最大父节点个数u，通过ch评分函数计算每个节点的结构评分，并将结构评分与初始评分进行比较，最终确定每个节点的父节点；

确定每个节点的父节点后，得到基于贝叶斯结构学习的航班保障关键点petri网。

本实施例的基于贝叶斯结构学习的航班保障petri网构建系统还包括时间分析单元、空间分析单元和评分分析单元。

时间分析单元，用于从时间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析，从分析中得到k2算法相对于贪心算法降低了时间复杂度。

空间分析单元，用于从空间复杂度对贪心算法和贝叶斯结构学习k2算法进行分析，从分析中得到k2算法相对于贪心算法降低了空间复杂度。

评分分析单元，用于从结构评分对航班保障计划流程关键点petri网和航班保障关键点petri网进行分析，从分析中得到航班保障关键点petri网更准确，更能体现航班真实流程。

本实施例为实施例一的方法对应的系统，其各单元的具体描述和分析，与实施例一相同，在此不再赘述。

综上所述，本实施例的系统，结合先验节点顺序、历史数据以及最大父节点个数，通过k2算法构建的航班保障关键点petri网，相比于航班保障计划流程关键点petri网，预测的结果更准确，更能准确反映航班保障关键节点的真实过程。

本领域普通技术人员可以意识到，结合本发明中所公开的实施例描述的各示例的单元及方法步骤，能够以电子硬件、计算机软件或者二者的结合来实现，为了清楚地说明硬件和软件的可互换性，在上述说明中已经按照功能一般性地描述了各示例的组成及步骤。这些功能究竟以硬件还是软件方式来执行，取决于技术方案的特定应用和设计约束条件。专业技术人员可以对每个特定的应用来使用不同方法来实现所描述的功能，但是这种实现不应认为超出本发明的范围。

在本申请所提供的几个实施例中，应该理解到，所描述的系统和方法，可以通过其它的方式实现。例如，以上所描述的方法实施例和系统实施例仅仅是示意性的，例如，所述单元的划分，仅仅为一种逻辑功能划分，实现时可以有另外的划分方式，例如多个单元或步骤可以结合为一个单元或步骤，或一些特征可以忽略，或不执行。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。