一种Burgers方程求解方法及装置与流程

本发明涉及移动电源技术领域，具体而言，涉及一种burgers方程求解方法及装置。

背景技术：

作为一种基础的非线性偏微分方程，burgers方程在流体力学、非线性声学、气体动力学等领域具有重要的应用。方程本身含有对流项、粘度项和时间依赖项，使其成为一个可以检测流体的数值算法的良好模型。至今为止提出的用于求解burgers方程的方法可以分为解析法和数值法。数值法运用数值近似和插值的方法对方程进行求解，一般分为有限差分法、有限元法、边界元法、有限体积法等。这几类方法运用相似的方式将空间域分成许多网格或单元，然后把流动方程在这些定义好的网格上进行离散，因此，网格的质量决定了计算结果的好坏。网格的重叠、变形和缠绕使这些基于网格的方法具有一定的缺陷，求解效率低，精度差。

针对上述的问题，目前尚未提出有效的解决方案。

技术实现要素：

本发明实施例提供了一种burgers方程求解方法及装置，以至少解决网格法求解burgers方程效率低，精度差的技术问题。

根据本发明实施例的一个方面，提供了一种基于无网格mlsph方法的burgers方程的求解方法，包括如下步骤：

步骤a、设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；

步骤b、基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；

步骤c、根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数，其中，第一时刻为相临两个时间步中的前一时间步对应的时刻；

步骤d、计算第一时刻物理量u对时间的导数；

步骤e、根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值，其中，第二时刻为相临两个时间步中的后一时间步对应的时刻；

步骤f、将第二时刻物理量u的值代入步骤c中，重复步骤c、步骤d、步骤e，得到所有时刻物理量u的值。

进一步地，基于无网格mlsph方法在定义域内进行数值离散得到的离散节点为均匀分布。

进一步地，无网格mlsph方法使用的核函数为五次样条型函数。

进一步地，无网格mlsph方法使用的核函数中的光滑长度与节点间隔的比值为1.1。

根据本发明实施例的另一方面，还提供了一种基于无网格mlsph方法的burgers方程的求解装置，包括：

设定模块，用于设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；

第一计算模块，用于基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；

第二计算模块，用于根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数，其中，第一时刻为相临两个时间步中的前一时间步对应的时刻；

第三计算模块，用于计算第一时刻物理量u对时间的导数；

第四计算模块，用于根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值，其中，第二时刻为相临两个时间步中的后一时间步对应的时刻；

循环模块，用于将第二时刻物理量u的值代入步骤c中，重复步骤c、步骤d、步骤e，得到所有时刻物理量u的值。

在本发明实施例中，采用如下步骤：步骤a、设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；步骤b、基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；步骤c、根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数；步骤d、计算第一时刻物理量u对时间的导数；步骤e、根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值；步骤f、将第二时刻物理量u的值代入步骤c中，重复步骤c、步骤d、步骤e，得到所有时刻物理量u的值，达到了求解burgers方程的目的，在求解过程中，无需将空间域分成许多网格或单元，进而解决了网格法求解burgers方程效率低，精度差的技术问题。

附图说明

此处所说明的附图用来提供对本发明的进一步理解，构成本申请的一部分，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：

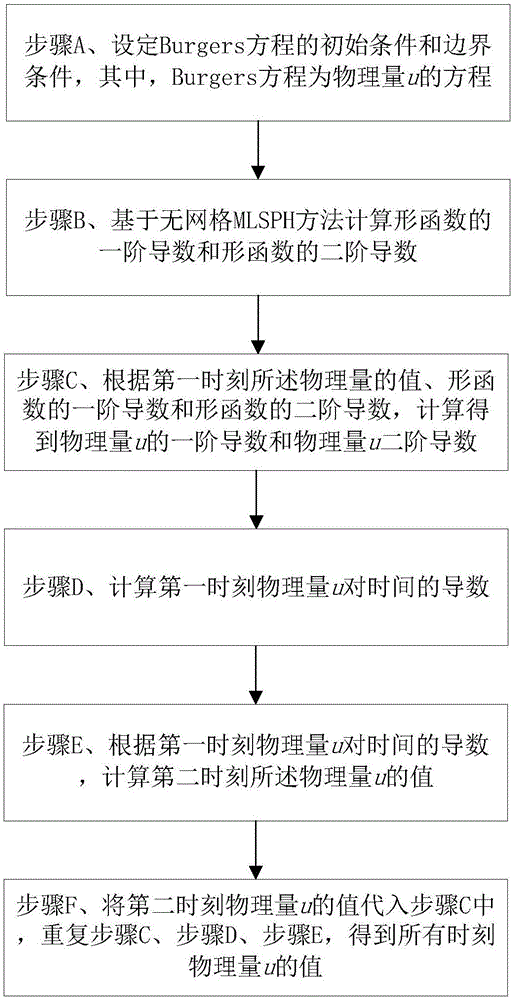
图1是根据本发明实施例的一种可选的基于无网格mlsph方法的burgers方程求解方法的流程图；

图2是根据本发明实施例的另一种可选的基于无网格mlsph方法的burgers方程求解装置的流程图；

图3是根据本发明实施例的一种可选的基于无网格mlsph方法的burgers方程求解装置的示意图。

具体实施方式

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分的实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。

需要说明的是，本发明的说明书和权利要求书及上述附图中的术语“第一”、“第二”等是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本发明的实施例能够以除了在这里图示或描述的那些以外的顺序实施。此外，术语“包括”和“具有”以及他们的任何变形，意图在于覆盖不排他的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。

根据本发明实施例，提供了基于无网格mlsph方法的burgers方程的求解方法，图1是根据本发明实施例的一种可选的基于无网格mlsph方法的burgers方程求解方法的流程图，如图1所示，该方法包括如下步骤：

步骤a、设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；burgers方程是模拟冲击波的传播和反射过程的非线性偏微分方程,一维burgers方程的表达式为其中，物理量u＝u(x,t)，d为扩散系数，可选的，在本实施例中其中re是雷诺系数，则burgers方程可以表示为设定burgers方程的初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，边界条件为

步骤b、基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；mlsph方法是一种无网格的粒子计算方法，它在定义域内分布的离散节点上，引入具有紧支域的核函数，然后求得移动最小二乘插值的形函数，再借助形函数进行求解。

可选地，在本实施例中，mlsph方法采用配点法进行数值离散，得到在定义域内分布的多个离散节点，进而运用移动最小二乘算法进行近似。

可选地，为了简化方程的求解过程，减少过程计算量，使计算结果稳定可靠，令在定义域内分布的多个离散节点为均匀分布。

由前述的burgers方程可知，burgers方程包含物理量u＝u(x,t)的一阶导数和二阶导数，在一个可选的实施例中，先计算形函数的一阶导数和二阶导数。

以连续的光滑函数f为例介绍形函数的一阶导数和二阶导数的计算方法。

连续的光滑函数f在位置坐标xi处有一系列函数值fi＝f(xi)，基于mlsph方法，f可近似为多项式其中，p^t(x)是n阶完整多项式基向量，m是项数，a(x)为系数向量。可选地，在三维条件下，x＝[xyz]^t，不同阶的向量p^t(x)可以具有不同的形式，如：一阶向量p^t(x)＝[1]，二阶向量p^t(x)＝[1xyz],三阶向量p^t(x)＝[1xyzxyxzyzx²y²z²]；系数向量a(x)＝argminj，通过计算近似值与实际值之间的误差的平方和可以构造范数j，可选地，令紧支域内的离散粒子数为n，核函数为w(x)。则

其中，h是光滑长度。

可选地，为了提高求解结果的精度，令mlsph方法使用的核函数中的光滑长度h与节点间隔的比值为1.1，其中，节点间隔δ＝xi+1-xi，xi和xi+1为任意两个相邻节点。

可选地，核函数w(x)是可微的，以便在后面的计算中对其进行微分。

可选地，为了提高计算结果的精度，令核函数w(x)为五次样条型核函数，可选地，当w(x)为五次样条型核函数时，其表达式如下：

其中，α代表空间维度，g是使核函数在定义域内的积分为1的标准化常数，可选地，当α＝1,2,3时，g的值分别为120，7/478π和3/359π。

可选地，在前述范数j的表达式中，令其中，k＝1,2,3,…，m。则得到其中，矩阵不依赖于粒子的函数值。进一步可以得到，光滑函数f的近似多项式。

其中wi(x)p^t(x)b(x)^-1p(xi)即为mlsph方法中的形函数，令φi(x)＝wi(x)p^t(x)b(x)^-1p(xi)，则至此，求得mlsph方法中的形函数φi(x)。

根据链式法则，形函数φi的一阶导数可以展开如下：

进一步可以得到形函数φi的二阶导数

可选地，由于形函数包含矩阵b的逆，为了使矩阵b在求逆的时候更加稳定，在一种可选的实施例中，多项式基以计算点为中心，增加矩阵b的条件数，可选的，可以令多项式基向量p(xi)为p((xi-x)/h)，

则改进后的矩阵最终的形函数为

步骤c、根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数，其中，第一时刻为相临两个时间步中的前一时间步对应的时刻；

前述步骤b中已知，函数f的近似多项式对该等式两边求导可得可知，函数f的一阶导数等于形函数的一阶导数乘以函数值。

可选地，由于已设定burgers方程的初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，则可以选择初始时刻t＝0为第一时刻，在按照步骤b计算得到形函数的一阶导数和二阶导数之后，根据burgers方程将初始时刻物理量u的值与步骤b中计算得到的形函数的一阶导数相乘，可以得到初始时刻物理量u的一阶导数值，同理，将初始时刻物理量u的值与形函数的二阶导数相乘得到初始时刻物理量u二阶导数值。

步骤d、计算第一时刻物理量u对时间的导数；根据burgers方程可知，burgers方程中物理量u对时间的导数值将步骤c中计算得到的物理量u的一阶导数和物理量u的二阶导数值代入burgers方程，可以计算得到物理量u对时间的导数值。

步骤e、根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值，其中，第二时刻为相临两个时间步中的后一时间步对应的时刻；

根据可知，后一时刻的物理量u的值可以根据前一时刻物理量u的值以及前一时刻物理量u对时间的导数值计算得到。

步骤f、将第二时刻物理量u的值代入步骤c中，重复步骤c、步骤d、步骤e，得到所有时刻物理量u的值。将步骤e中计算得到的第二时刻物理量u的值代入步骤c中，即将第二时刻作为新的第一时刻，重复步骤c、步骤d、步骤e，循环计算直到计算出所有时刻物理量u的值。

在本发明实施例中，采用如下步骤：步骤a、设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；步骤b、基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；步骤c、根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数；步骤d、计算第一时刻物理量u对时间的导数；步骤e、根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值；步骤f、将第二时刻物理量u的值代入步骤c中，重复步骤c、步骤d、步骤e，得到所有时刻物理量u的值，达到了求解burgers方程的目的，在求解过程中，无需将空间域分成许多网格或单元，进而解决了网格法求解burgers方程效率低，精度差的技术问题。

图2是根据本发明实施例的另一种可选的基于无网格mlsph方法的burgers方程求解装置的流程图，如图2所示，该方法包括：

步骤s201,定义初始条件和边界条件；一维burgers方程的表达式为其中，物理量u＝u(x,t)，d为扩散系数，可选地，设定burgers方程的初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，边界条件为

步骤s202,在定义域内离散节点；可选地，mlsph方法采用配点法进行数值离散，得到在定义域内分布的多个离散节点，

可选地，在定义域内分布的多个离散节点为均匀分布。

步骤s203，计算mlsph方法中的形函数的一阶导数和二阶导数；令mlsph方法中的核函数为w(x)，则形函数φi(x)＝wi(x)p^t(x)b(x)^-1p(xi)，其中，p^t(x)是n阶完整多项式基向量，矩阵形函数φi的一阶导数可以展开如下：

进一步可以得到形函数φi的二阶导数

步骤s204,开始时间步；可选地，时间步满足关系式tl+1＝tl+δt，其中，tl和tl+1为相临的两个时间步，tl为前一时间步，tl+1为后一时间步。

步骤s205,计算物理量u的一阶导数和二阶导数值；由于已设定初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，可以计算得到初始时刻物理理u的一阶导数值和二阶导数值，初始时刻物理理u的一阶导数值为初始时刻物理量u的值与形函数的一阶导数的乘积，初始时刻物理理u的二阶导数值为初始时刻物理量u的值与形函数的二阶导数的乘积。

步骤s206,根据burgers方程计算物理量u对时间的导数；根据burgers方程可知，burgers方程中物理量u对时间的导数值因此，根据初始时刻物理理u的一阶导数值、初始时刻物理理u的二阶导数值，可以计算得到初始时刻物理量u对时间的导数。

步骤s207,更新u值；根据可知，后一时刻的物理量u的值可以根据前一时刻物理量u的值以及前一时刻物理量u对时间的导数值计算得到，因此，在计算得到初始时刻物理量u对时间的导数之后，可以进一步计算得到下一时刻物理量u的值，将下一时刻物理量u的值作为当前时刻物理量的值。

步骤s208，输出u值；将更新得到的当前时刻的物理量的值输出。

步骤s209,判断是否结束时间步。判断当前时刻对应的时间步是否为最终的时间步，如果不是，则跳转至步骤s205,如果当前时刻对应的时间步是最终的时间步，则步骤结束。

图3是根据本发明实施例的一种可选的基于无网格mlsph方法的burgers方程求解装置的示意图，如图3所示，该装置包括:

设定模块31，用于设定burgers方程的初始条件和边界条件，其中，burgers方程为物理量u的方程；burgers方程是模拟冲击波的传播和反射过程的非线性偏微分方程,一维burgers方程的表达式为其中，物理量u＝u(x,t)，d为扩散系数，可选的，在本实施例中其中re是雷诺系数，则burgers方程可以表示为设定burgers方程的初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，边界条件为

第一计算模块32，用于基于无网格mlsph方法计算形函数的一阶导数和形函数的二阶导数；mlsph方法是一种无网格的粒子计算方法，它在定义域内分布的离散节点上，引入具有紧支域的核函数，然后求得移动最小二乘插值的形函数，再借助形函数进行求解。

可选地，在本实施例中，mlsph方法采用配点法进行数值离散，得到在定义域内分布的多个离散节点，进而运用移动最小二乘算法进行近似。

可选地，在定义域内分布的多个离散节点为均匀分布。

由前述的burgers方程可知，burgers方程包含物理量u＝u(x,t)的一阶导数和二阶导数，在一个可选的实施例中，先计算形函数的一阶导数和二阶导数。

以连续的光滑函数f为例介绍形函数的一阶导数和二阶导数的计算方法。

连续的光滑函数f在位置坐标xi处有一系列函数值fi＝f(xi)，基于mlsph方法，f可近似为多项式其中，p^t(x)是n阶完整多项式基向量，m是项数，a(x)为系数向量。可选地，在三维条件下，x＝[xyz]^t，不同阶的向量p^t(x)可以具有不同的形式，如：一阶向量p^t(x)＝[1]，二阶向量p^t(x)＝[1xyz],三阶向量p^t(x)＝[1xyzxyxzyzx²y²z²]；系数向量a(x)＝argminj，通过计算近似值与实际值之间的误差的平方和可以构造范数j，可选地，令紧支域内的离散粒子数为n，核函数为w(x)。则

其中，h是光滑长度。

可选地，mlsph方法使用的核函数中的光滑长度h与节点间隔的比值为1.1

可选地，令核函数w(x)为五次样条型核函数。

可选地，核函数w(x)是可微的，以便在后面的计算中对其进行微分。

可选地，在前述范数j的表达式中，令其中，k＝1,2,3,…，m。则得到其中，矩阵不依赖于粒子的函数值。进一步可以得到，光滑函数f的近似多项式

其中wi(x)p^t(x)b(x)^-1p(xi)即为mlsph方法中的形函数，令φi(x)＝wi(x)p^t(x)b(x)^-1p(xi)，则至此，求得mlsph方法中的形函数φi(x)。

根据链式法则，形函数φi的一阶导数可以展开如下：

进一步可以得到形函数φi的二阶导数

可选地，由于形函数包含矩阵b的逆，为了使矩阵b在求逆的时候更加稳定，在一种可选的实施例中，多项式基以计算点为中心，增加矩阵b的条件数，可选的，可以令多项式基向量p(xi)为p((xi-x)/h)，

则改进后的矩阵最终的形函数为

第二计算模块33，用于根据第一时刻物理量u的值、形函数的一阶导数和形函数的二阶导数，计算得到物理量u的一阶导数和物理量u二阶导数，其中，第一时刻为相临两个时间步中的前一时间步对应的时刻；

前述已知，函数f的近似多项式对该等式两边求导可得可知，函数f的一阶导数等于形函数的一阶导数乘以函数值。

可选地，由于已设定burgers方程的初始条件为u(x,0)＝sin(πx),其中，0＜x＜1，则可以选择初始时刻t＝0为第一时刻，在第一计算模块计算得到形函数的一阶导数和二阶导数之后，根据burgers方程将初始时刻物理量u的值与第一计算模块计算得到的形函数的一阶导数相乘，可以得到初始时刻物理量u的一阶导数值，同理，将初始时刻物理量u的值与形函数的二阶导数相乘得到初始时刻物理量u二阶导数值。

第三计算模块34，用于计算第一时刻物理量u对时间的导数；根据burgers方程可知，burgers方程中物理量u对时间的导数值将第二计算模块计算得到的物理量u的一阶导数和物理量u的二阶导数值代入burgers方程，可以计算得到物理量u对时间的导数值。

第四计算模块35，用于根据第一时刻物理量u对时间的导数，计算第二时刻物理量u的值，其中，第二时刻为相临两个时间步中的后一时间步对应的时刻；

根据可知，后一时刻的物理量u的值可以根据前一时刻物理量u的值以及前一时刻物理量u对时间的导数值计算得到。

循环模块36，用于将第二时刻物理量u的值代入第二计算模块中，重复执行第二计算模块、第三计算模块、第四计算模块，得到所有时刻物理量u的值。将第四计算模块计算得到的第二时刻物理量u的值代入第二计算模块中，即将第二时刻作为新的第一时刻，重复执行第二计算模块、第三计算模块、第四计算模块，循环计算直到计算出所有时刻物理量u的值。

上述本发明实施例序号仅仅为了描述，不代表实施例的优劣。

在本发明的上述实施例中，对各个实施例的描述都各有侧重，某个实施例中没有详述的部分，可以参见其他实施例的相关描述。

在本申请所提供的几个实施例中，应该理解到，所揭露的技术内容，可通过其它的方式实现。其中，以上所描述的装置实施例仅仅是示意性的，例如所述单元的划分，可以为一种逻辑功能划分，实际实现时可以有另外的划分方式，例如多个单元或组件可以结合或者可以集成到另一个系统，或一些特征可以忽略，或不执行。另一点，所显示或讨论的相互之间的耦合或直接耦合或通信连接可以是通过一些接口，单元或模块的间接耦合或通信连接，可以是电性或其它的形式。

所述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物理单元，即可以位于一个地方，或者也可以分布到多个单元上。可以根据实际的需要选择其中的部分或者全部单元来实现本实施例方案的目的。

另外，在本发明各个实施例中的各功能单元可以集成在一个处理单元中，也可以是各个单元单独物理存在，也可以两个或两个以上单元集成在一个单元中。上述集成的单元既可以采用硬件的形式实现，也可以采用软件功能单元的形式实现。

所述集成的单元如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的全部或部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可为个人计算机、服务器或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：u盘、只读存储器(rom，read-onlymemory)、随机存取存储器(ram，randomaccessmemory)、移动硬盘、磁碟或者光盘等各种可以存储程序代码的介质。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。