一种基于空间变换原理的摆焊方法与流程

本发明属于机器人技术领域，尤其涉及一种基于空间变换原理的摆焊方法。

背景技术：

摆弧运动是进行弧焊作业时特有的一种运动形式,用摆弧技术进行宽焊缝或空间中焊缝焊接,焊接效果更好，同时该技术也是实现焊接自动化的重要技术之一。摆弧技术作为焊接机器人的关键技术，相关算法大多是保密的，公开的相关资料较少，哈尔滨工业大学的杨海涛提出了基于空间矢量位置法的摆弧运动方案，可以实现基础的空间摆弧运动。华中科技大学的熊烁针对这个问题提出了一种基于轨迹叠加思路的运动方案，但并未深入介绍。这些算法虽然都能完成摆焊的基础动作，但是均有着输入参数少，摆动轨迹简单，运算量大的特点。

技术实现要素：

本发明提出了一种基于空间变换原理的摆焊方法，可以克服上述摆弧方案缺点，实现多种控制参数输入，完成复杂的圆弧轨迹摆焊。

为实现上述目的，本发明采用如下的技术发方案：

一种基于空间变换原理的摆焊方法，包括以下步骤：

步骤1、摆动平面模型的建立

(1)首先建立摆动基础平面xoy，摆动节点将根据摆动参数在摆动基础平面求解，之后再经过变换映射到真实摆动平面；xoy平面经过平移并绕动坐标系旋转三次旋转得到真实摆动平面，这三次旋转依次是，先绕着z轴旋转对应角度α，然后绕y轴旋转β，最后绕着x轴旋转γ，

(2)求解摆动平面的变换矩阵，假设示教三点的坐标分别为pa(xa,ya,za)、pb(xb,yb,zb)和pc(xc,yc,zc)，且ac两点的距离dxy≠0，分别对α，β，γ求解。根据几何关系可知：

α＝atan2(yb-ya，xb-xa)(1)

设线段ab的长度为d，则：

经过绕z轴旋转α，及绕y轴旋β两次旋转后，新坐标系的z轴指向的单位向量新坐标系的x轴指向的单位向量为分别为：

设真实摆动平面的法向量为n，则：

由(4)、(5)、(6)可得

求解出(α，β，γ)之后，可得由基础平面到摆动平面的旋转矩阵：

在建立模型时，假设条件是dxy≠0，当dxy＝0时，此时旋转矩阵有两种情况：

当zc＞za时：

当zc＜za时：

通过上述分析可以得到由摆动基础平面xoy到真实摆动平面的齐次变换矩阵：

可以通过在基础平面计算出摆动节点，然后每个点经过旋转平移得到相应的圆弧摆动点；

步骤2、平面摆动点的计算

通过建立摆动基础平面简化复杂的空间问题，基础平面摆动点计算如下：

(1)设pa,pb,pc在摆动基础平面的映射点分别为pa1,pb1,pc1则根据pa1,pb1,pc1三点坐标求出圆心o(xo,yo,0)及半径r，

(2)进行一次平移变换t，将圆心o(xo,yo,0)平移至摆动基础平面xoy的原点。得到平移后的点pao(xao,yao,0)、pbo(xbo,ybo,0)、pco(xco,yco,0)，以及圆弧

(3)确定摆动基本参数，设三次停留时间分别为t1,t2,t3，单次波形频率可由上位输入设为f，上位传输的焊接速度为v，则：

对应的角速度为：

ω＝v/r(11)

各停留时间运动弧度为：

单次波形四分之一周期走过弧度为：

se＝ω/4f(13)

单次摆动周期内运动的弧度为：

l＝4se+s1+s2+s3(14)

(4)为保证摆焊轨迹可靠的通过示教点pb(xb,yb,zb)，将拆分为两段，分别表示为及基础平面摆动点在两段圆弧上利用相同的算法分别求解，

(5)求解基础平面摆动点，首先计算圆弧的起始和终止角度，以段为例，圆弧段的起始角度和终止角度分别为θs、θe则：

设上位输入左右前后角为φl和φr，则周期内基本点的递推公式为：

其中i＝1,2,3...n，其中

(6)计算全部基本摆动点，设stepi代表这个步骤所要计算的坐标(xi,yi,zi)，ls为stepi(i＝1...8)内得到相应坐标后所剩余的弧度，step9表示循环进入最后一个点的计算，最后一个点的坐标为下个示教点的坐标；

步骤3、真实摆动点的求解

假设基础摆动点为pi(xi,yi,zi)，真实摆动点为pi(xi,yi,zi)，则空间摆动点的计算公式^[6]：

由式(18)可求出空间摆动点的坐标。

附图说明

图1焊接摆动参数，其中，图1(a)为振幅，图1(b)为停留时间，图1(c)为前后角；

图2摆动平面；

图3圆弧摆动节点示意图；

图4摆动点计算流程图；

图5单段圆弧摆动轨迹，其中，图5(a)1/4,2/4,3/4处停留时间均不为0，图5(b)左前角为负，右前角为0；

图6空间多段圆弧摆动轨迹。

具体实施方式

用摆焊焊缝的质量与焊接摆动参数有很大的关系；示教轨迹与摆动参数的设置共同决定了焊接机器人的摆动类型和轨迹。本发明提出的基于空间变换原理的摆焊算法可以实现以下参数的设置：

(1)摆动频率。

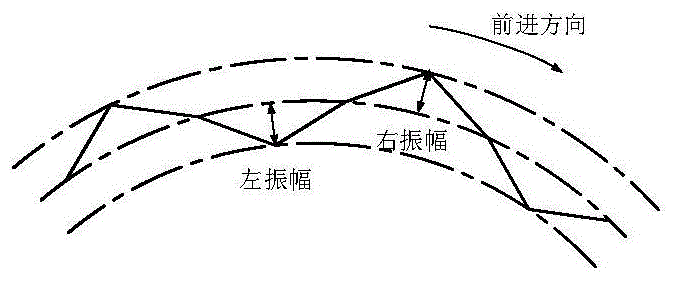
(2)振幅：即摆焊时从焊缝中心往左右摆动的最大距离，如图1(a)所示。

(3)停止时间：停止时间指的是在每个周期的1/4,2/4，3/4处摆弧停止的时间，如图1(b)所示。通过停留时间的设置可以实现梯形摆动及其他摆动类型。

(4)前后角：指的是摆动方向与前进方向的垂直方向的角度，如图1(c)所示。当前后角不为零时，摆动偏离焊缝中心的最大距离将小于振幅的值。

本发明提供一种基于空间变换原理的摆焊方法，包括以下步骤：

步骤1、摆动平面模型的建立

(3)首先建立摆动基础平面xoy，摆动节点将根据摆动参数在摆动基础平面求解，之后再经过变换映射到真实摆动平面。xoy平面经过平移并绕动坐标系旋转三次旋转得到真实摆动平面，这三次旋转依次是，先绕着z轴旋转对应角度α，然后绕y轴旋转β，最后绕着x轴旋转γ。摆动平面与基础坐标系的变换关系如图2所示:

(4)求解摆动平面的变换矩阵。由图2可得，只要求出了对应的三个旋转角度，就可求出对应的旋转矩阵。假设示教三点的坐标分别为pa(xa,ya,za)、pb(xb,yb,zb)和pc(xc,yc,zc)，且ac两点的距离dxy≠0，分别对α，β，γ求解。根据几何关系可知：

α＝atan2(yb-ya，xb-xa)(1)

设线段ab的长度为d，则：

经过绕z轴旋转α，及绕y轴旋β两次旋转后，新坐标系的z轴指向的单位向量新坐标系的x轴指向的单位向量为分别为：

设真实摆动平面的法向量为n，则：

由(4)、(5)、(6)可得

求解出(α，β，γ)之后，可得由基础平面到摆动平面的旋转矩阵：

在建立模型时，假设条件是dxy≠0，当dxy＝0时，此时旋转矩阵有两种情况：

当zc＞za时：

当zc＜za时：

通过上述分析可以得到由摆动基础平面xoy到真实摆动平面的齐次变换矩阵：

这样就可以通过在基础平面计算出摆动节点，然后每个点经过旋转平移得到相应的圆弧摆动点。

步骤2、平面摆动点的计算

通过建立摆动基础平面简化复杂的空间问题，基础平面摆动点计算如下：

(3)设pa,pb,pc在摆动基础平面的映射点分别为pa1,pb1,pc1则根据pa1,pb1,pc1三点坐标求出圆心o(xo,yo,0)及半径r。

(4)进行一次平移变换t，将圆心o(xo,yo,0)平移至摆动基础平面xoy的原点。得到平移后的点pao(xao,yao,0)、pbo(xbo,ybo,0)、pco(xco,yco,0)，以及圆弧

(3)确定摆动基本参数，设三次停留时间分别为t1,t2,t3，单次波形频率可由上位输入设为f，上位传输的焊接速度为v，则：

对应的角速度为：

ω＝v/r(11)

各停留时间运动弧度为：

单次波形四分之一周期走过弧度为：

se＝ω/4f(13)

单次摆动周期内运动的弧度为：

l＝4se+s1+s2+s3(14)

(7)为保证摆焊轨迹可靠的通过示教点pb(xb,yb,zb)，将拆分为两段，分别表示为及基础平面摆动点在两段圆弧上利用相同的算法分别求解。

(8)求解基础平面摆动点，首先计算圆弧的起始和终止角度。以段为例，圆弧段的起始角度和终止角度分别为θs、θe则：

设上位输入左右前后角为φl和φr，则周期内基本点的递推公式为：

其中i＝1,2,3...n，其中根据摆动参数画出求解摆动点的图形如图3所示：

(9)根据图4计算全部基本摆动点，设stepi代表这个步骤所要计算的坐标(xi,yi,zi)，ls为stepi(i＝1...8)内得到相应坐标后所剩余的弧度，step9表示循环进入最后一个点的计算，最后一个点的坐标为下个示教点的坐标；具体为：

首先，判断当前示教弧度是否大于单次波形四分之一周期走过弧度减去左前后角的弧度，如果大于，则进入step1，如果小于或等于则进入step9；进入step1之后判断四分之一停留时间是否为0，如果为零，则进入step3，如果不为零，则判断剩余弧长是否大于四分之一停留时间运动弧度，如果大于则进入step2，如果小于或等于则进入step9。进入step2之后判断剩余弧长是否大于单次波形四分之一周期走过弧度加上左前后角的弧度，如果大于，则进入step3，如果小于或等于则进入step9；进入step3之后判断四分之二停留时间是否为0，如果为零，则进入step5，如果不为零，则判断剩余弧长是否大于四分之二停留时间运动弧度，如果大于则进入step4，如果小于或等于则进入step9。进入step4之后判断剩余弧长是否大于单次波形四分之一周期走过弧度减去右前后角的弧度，如果大于，则进入step5，如果小于或等于则进入step9；进入step5之后判断四分之三停留时间是否为0，如果为零，则进入step7，如果不为零，则判断剩余弧长是否大于四分之三停留时间运动弧度，如果大于则进入step6，如果小于或等于则进入step9。进入step6之后判断剩余弧长是否大于单次波形四分之一周期走过弧度加上右前后角的弧度，如果大于，则进入step7，如果小于或等于则进入step9；进入step7之后判断四分之二停留时间是否为0，如果为零，则重新进入step1，如果不为零，则判断剩余弧长是否大于四分之二停留时间运动弧度，如果大于则进入step8，如果小于或等于则进入step9。进入step8之后判断剩余弧长是否大于单次波形四分之一周期走过弧度减去左前后角的弧度，如果大于，则重新进入step1，如果小于或等于则进入step9；经过一次或多次循环之后，流程将最终终止于step9，其中stepi(i＝1...9)的具体计算公式见公式(17)。

步骤3、真实摆动点的求解

假设基础摆动点为pi(xi,yi,zi)，真实摆动点为pi(xi,yi,zi)，则空间摆动点的计算公式^[6]：

由式(18)可求出空间摆动点的坐标。

为检验算法的正确性及可行性，将算法封装成摆动功能函数，于仿真环境中进行验证。摆动功能函数接收示教点，以及相关的摆动参数，通过计算，生成相应的摆动轨迹文件。单段圆弧与空间多段圆弧摆动轨迹分别如图5(a)、图5(b)、图6所示，图中红色轨迹为摆动段示教轨迹。