一种基于高斯回归的空间细粒度污染推断方法与流程

本发明涉及环境监测领域，尤其涉及一种基于高斯回归的空间细粒度污染推断方法。

背景技术：

为了精细的研究pm2.5的产生、扩散规律，需要有更密集部署的监测系统，目前我国在各个主要的城市均部署了精准的国控站进行监测，但监测密度仍然非常稀疏，例如北京大约一万平方公里面积只有35个国控站点进行监测，这对于精准的空间推断，以及之后的精细管控、健康风险评估均构成了很大的挑战。相关研究表明，即使相距较近的两地，其pm2.5也可能存在较大的差距。

为了对空间的污染监测数据进行推断，近年来提出了两类主要的方法。第一类为传统的扩散模型，如高斯煙羽模式，三维街谷模型和计算流体力学模型。这些模型通常综合了诸如气象信息，街道地理特征信息，交通信息等众多数据，并进行复杂的数据建模，但是这类模型通常需要对物理环境进行较为强烈的假设，同时又需要各种纬度精细的监测数据，而这些对于空气污染监测领域而言，获取相对较难。第二类模型基于空间推断，这类模型基于城市内已经监测得倒的稀疏国控站点的数据，并结合气象、地理位置，交通信息等数据，建立空间统计推断模型，从而对未知地点的污染数值进行推断。但是，对于未部署国控站点的区域并不能准确推断出该区域的数据，因此如何有效利用有限的数据对未部署地点进行50米精度的推测是目前亟待解决的问题。

技术实现要素：

本发明的目的在于提供一种基于高斯回归的空间细粒度污染推断方法，从而解决现有技术中存在的前述问题。

为了实现上述目的，本发明采用的技术方案如下：

1.一种基于高斯回归的空间细粒度污染推断方法，包括以下步骤：

s1，定义给定监测区域内所有监测点位的数据，对所有未知点位的pm2.5的数值进行推断；

s2，确定选用的高斯回归模型，使用该高斯回归模型进行数据训练；

s3，选用训练数据和测试数据，并利用训练数据和测试数据获得待推断空间细粒度污染预测值。

优选地，步骤s1中定义给定的数据具体为：

xi表示监测区域内第i个监测站的经纬度，使用yi表示该监测点位的pm2.5的数值；

对所有未知点位的pm2.5的数值进行推断的公式为：

其中∈i表示噪声。

本方法的目标为对于给定的数据，学习得出正确的函数f，从而能对任意给定的x，预测其对应的y。

高斯过程为一统计学分布，是一系列关于连续域(时间或空间)的随机变量的联合，而且针对每一个时间点或空间点上的随机变量都是服从高斯分布的。在高斯回归问题中，函数f分布服从高斯分布(正态分布)，

优选地，步骤s2中具体过程包括：

s21，定义fi＝f(xi)；

s22，当x满足下述条件：

其中k是协方差矩阵，其中kij＝k(xi,xj)，k(x1,x2)可以是任何满足半正定特征的核函数，其中k是协方差矩阵。

优选地，所述核函数选用下述的平方指数协方差函数：

其中l表示该函数水平变化的尺度。

优选地，步骤s3具体包括：

s31,使f＝[f1,f2,...,fn],f*＝[f*1,f*2,...,f*n]分别表示训练数据和测试数据；

s32，使用贝叶斯理论，得到：

s33，根据上式得到后验概率分布:

s34，先验概率及似然函数都为独立分布且均服从高斯分布：

其中δ²是噪声方差，i是单位矩阵；

从而公式(5)中的积分可以得到完全解，其解同时也服从高斯分布

μ*＝k*,f(kf,f+δ²i)^-1y(7)

σ*＝k*,*-k*,f(kf,f+δ²i)^-1kf,*(8)

μ*是预测均值，σ*是其对应的预测方差，即预测值对应的置信度，在我们的使用场景中，我们使用μ*i作为我们对于yi的预测值。

本发明的有益效果是：

本发明公开了一种基于高斯回归的空间细粒度污染推断方法，该方法与其他污染推测方法相比具有较高的准确性和稳定性，更加适合对细粒度pm2.5进行空间推断；精细的污染热图使得后续的精细污染管控及健康风险评估具有更大的可能性。

附图说明

图1是北京市部署的pm2.5监测站点的数据部署图；

图2是实施例2中两个点位数据差距分布图；

图3是实施例2中水平尺度参数与空间推断绝对误差之间的关系；

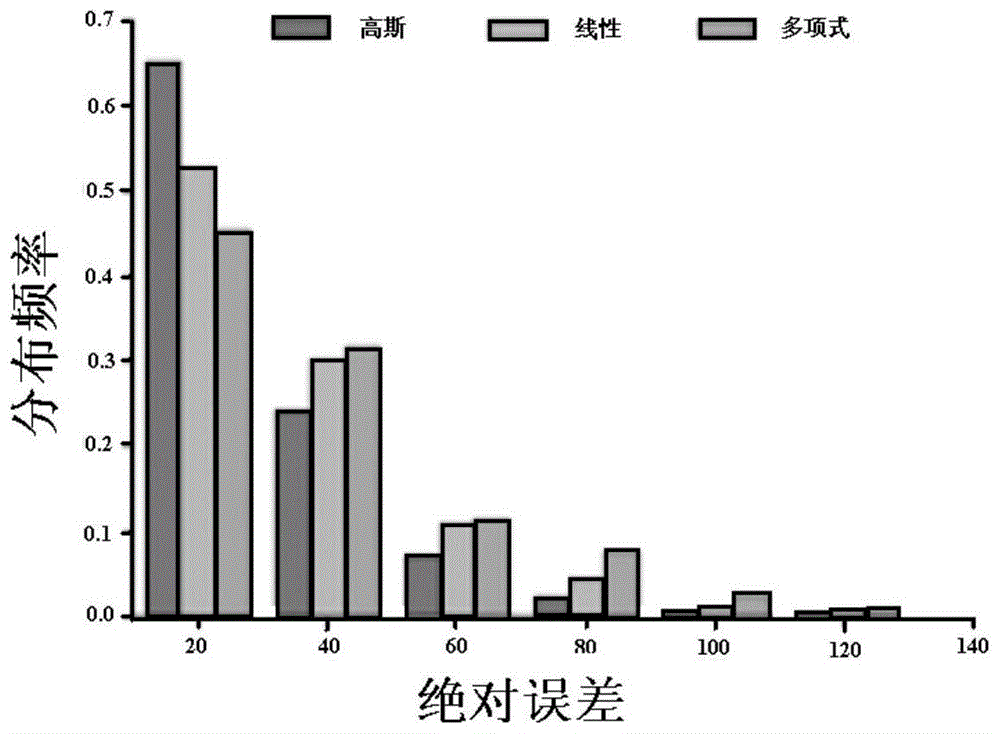
图4是实施例2中使用不同的三种方法做空间推断的绝对误差分布统计；

图5是实施例2中8个监测站点的空间推断误差柱状图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施方式仅仅用以解释本发明，并不用于限定本发明。

实施例1

本实施例公开一种基于高斯回归的空间细粒度污染推断方法，包括以下步骤：

s1，定义给定监测区域内所有监测点位的数据，对所有未知点位的pm2.5的数值进行推断；

使用xi表示监测区域内第i个监测站的经纬度，使用yi表示该监测点位的pm2.5的数值。该问题可以定义为给定监测区域内所有监测点位的数据对所有未知点位的pm2.5的数值进行推断。这是一个典型的数值回归问题，可以进行如下的定义：

其中∈i表示噪声。本方法的目标为对于给定的数据，学习得出正确的函数f，从而能对任意给定的x，预测其对应的y。

步骤二、确定高斯回归模型(确定协方差函数)

高斯过程为一统计学分布，是一系列关于连续域(时间或空间)的随机变量的联合，而且针对每一个时间点或空间点上的随机变量都是服从高斯分布的。在高斯回归问题中，函数f分布服从高斯分布(正态分布)，当x满足下述条件：

其中fi＝f(xi)表示上述的函数f，其中k是协方差矩阵，其中kij＝k(xi,xj).k(x1,x2)可以是任何满足半正定特征的核函数。

步骤三、利用训练数据和测试数据获得预测值

在算法的推断过程中，使f＝[f1,f2,...,fn],f*＝[f*1,f*2,...,f*n]分别表示训练数据和测试数据。进而，使用贝叶斯理论，可以得到：

通过上式，可以进一步得到后验概率分布：

因为先验概率及似然函数都为独立分布且均服从高斯分布：

其中δ²是噪声方差，i是单位矩阵。从而公式(4)中的积分可以得到完全解，其解同时也服从高斯分布

μ*＝k*,f(kf,f+δ²i)^-1y(6)

σ*＝k*,*-k*,f(kf,f+δ²i)^-1kf,*(7)

其中μ*是预测均值，σ*是其对应的预测方差，即预测值对应的置信度。在我们的使用场景中，我们使用μ*i作为我们对于yi的预测值。

实施例2

本实施例使用部署在北京市部署的pm2.5监测站点的数据，数据每小时更新一次，部署图如下图1所示，对高斯回归模型的推断性能进行分析。

图2所示为两个点位数据差距分布图，从图2中可以看出，虽然两点位距离相差不远，但是其pm2.5数据依然可能存在较大的差距，这两个点位相距6千米，但是超过21％情况下其绝对误差大于100。

实际预测中，我们随机去除一个点位，并利用其余点位的数据对其进行预测。

步骤一、给出问题的具体定义

使用xi表示监测区域内第i个监测站的经纬度，使用yi表示该监测点位的pm2.5的数值。该问题可以定义为给定监测区域内所有监测点位的数据对所有未知点位的pm2.5的数值进行推断。这是一个典型的数值回归问题，可以进行如下的定义：

其中∈i表示噪声。本模型的目标为对于给定的数据，学习得出正确的函数f，从而能对任意给定的x，预测其对应的y。

步骤二、确定高斯回归模型(确定协方差函数)

高斯过程为一统计学分布，是一系列关于连续域(时间或空间)的随机变量的联合，而且针对每一个时间点或空间点上的随机变量都是服从高斯分布的。在高斯回归问题中，函数f分布服从高斯分布(正态分布)，当x满足下述条件：

其中fi＝f(xi)表示上述的函数f，其中k是协方差矩阵，其中kij＝k(xi,xj).k(x1,x2)可以是任何满足半正定特征的核函数。

选用下述的平方指数协方差函数：

其中l表示该函数水平变化的尺度。当l变大时，相对应的特征纬度便会变的相对不重要，反之亦然。当选用一个较大的l值，但是空间推断的效果依然较好时，反映了该区域范围内pm2.5的分布相对较为平缓，反之反映了该区域的pm2.5分布非线性，因此，l的选择反映了pm2.5分布的特征。

图3表示了水平尺度参数与空间推断绝对误差之间的关系。随着l的增加，空间推断的误差从27.6降低到了21.9，这表明pm2.5的分布在绝大部分的情况下是非线性的，当两地相距较大时，其数据可能存在较大的差距。

步骤三、利用训练数据和测试数据获得预测值

在算法的推断过程中，使f＝[f1,f2,...,fn],f*＝[f*1,f*2,...,f*n]分别表示训练数据和测试数据。进而，使用贝叶斯理论，可以得到：

通过上式，可以进一步得到后验概率分布：

因为先验概率及似然函数都为独立分布且均服从高斯分布：

其中δ²是噪声方差，i是单位矩阵。从而公式(5)中的积分可以得到完全解，其解同时也服从高斯分布

μ*＝k*,f(kf,f+δ²i)^-1y(7)

σ*＝k*,*-k*,f(kf,f+δ²i)^-1kf,*(8)

其中μ*是预测均值，σ*是其对应的预测方差，即预测值对应的置信度。在本发明中μ*i作为我们对于yi的预测值。

图4显示了使用不同的三种方法做空间推断的绝对误差分布统计。可以看出，本实施例中的采用高斯回归模型的推断方法明显好于线性模型及多项式推断模型。高斯推断方法的65％的结果处于误差20以内，相对应的，线性模型为52％，多项式模型为46％。同时，可以看出，线性模型的效果要好于多项式模型，但是并不表示pm2.5在空间上时线性分布的。图5中显示了8个监测站点的空间推断误差柱状图。从图中可以看出，站点24，25，38线性模型要好于多项式模型，而站点7，12，47多项式模型的性能要好于线性模型，这表明在一些地点pm2.5的分布偏移线性分布，而相对应的，在另外一些地点，其分布可能是非线性的。而在基本所有的情况下，高斯回归模型均好于线性及多项式模型，这也表明了高斯回归模型在pm2.5空间推断中的有效性。

表1显示了三种不同的方法的空间推断的误差统计结果。

从表中可以看出，高斯推断模型效果要明显好于线性及多项式模型。在切比雪夫范数误差统计中，线性及多项式模型均高达266.92，而高斯模型降低至154.14，这表明高斯推断模型在pm2.5的空间推断中具有更好的稳定性。

通过采用本发明公开的上述技术方案，得到了如下有益的效果：

本发明公开了一种基于高斯回归档空间细粒度污染推断方法，首先对问题进行科学定义，目的是对所有未知点位的pm2.5的数值进行推断，然后利用高斯回归模型对300个网络节点获得的pm2.5数据进行分析，以此来对所有未知点位的pm2.5的数值进行推断，最后利用协方差函数来衡量距离相似度。本发明给出的模型是高斯过程模型，该模型提供预测方差，表明局部随机区域中预测的有效性，而传统线性模型多项式模型则不然。

本发明与现有技术相比具有以下优点：1、本发明中的采用高斯回归模型的方法与采用其他模型的推断方法相比具有较高的准确性和模型稳定性，更加适合对细粒度pm2.5进行空间推断；2、精细的污染热图使得后续的精细污染管控及健康风险评估具有更大的可能性。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视本发明的保护范围。