基于Caputo型分数阶微分的不确定电路可靠性分析方法

本发明涉及一阶串联式rc电路系统优化的可靠性分析，具体涉及一种基于caputo型分数阶微分的不确定电路可靠性分析方法。

背景技术：

可靠性分析的目的是为了反映当前设备产品真实的可靠性水平，发现其存在的隐患和薄弱环节，从而促进在设备的研制、设计、生产及使用过程中的安全性和可靠性。然而，由于众多因素导致现有可靠新分析方法存在挑战，这些因素包括：(1)传感器设计或观测者自身所固有的局限性；(2)在观测时间和空间上的限制，以及观测过程中存在着诸多非可预测因素；(3)内外部因素影响下系统的非可预知性变化；(4)在信息的加工处理中所用方法的不完备性，在实际工程应用中，电路系统的可靠性受大量不确定性因素干扰。这些不确定性因素导致现存可靠性分析方法面临两大挑战：1)复杂电路系统呈现出现有模型无法全面解释的的全局相关性；2)复杂电路系统的可靠性分析缺乏失效数据。

首先，随着越来越多诸如湍流速度场的不可微性、黏弹性材料应力松弛的记忆性等反常现象的出现，学者们发现这些复杂的物理现象具有一个共同的特征，即幂律性。这一性质赋予了真实复杂系统中无处不在的全局相关性。即使是简单的电路单元(如一阶rc电路)，都展现出与经典理论截然不同的复杂性质。然而长期以来，对于电路系统的可靠性分析技术惯于利用整数阶微分方程来建立各种复杂电路系统的模型，无法刻画出电路系统的这种幂律性。

其次，现存基于概率统计的传统可靠性分析方法对设备产品可靠性试验获得的大量数据或实际使用中的大量失效数据有较强依赖性。然而，客观条件限制导致的可靠性数据的缺乏往往使得这类方法难以有效实施。特别地，对于大型复杂系统，在方案论证和系统设计早期阶段，能够用于分析的失效数据样本量较小，因而基于大样本数据的概率模型和统计方法适用度低。因此，对于复杂电路系统及其组成单元，其可靠性有时会以专家意见等定性信息描述。然而，这种定性描述对于不确定性环境下的电路系统中的事件信度，是缺乏精确性的。

因此，有必要从实际情况下的简单电路出发，提出一种针对不确定电路的更准确的可靠性分析方法。

技术实现要素：

发明目的：针对现有技术的缺陷和不足，本发明提出一种基于caputo型分数阶微分的不确定电路可靠性分析方法，在考虑不确定性因素的前提下，建立符合实际情况的一阶串联式rc电路系统模型，对一阶串联式rc电路系统的可靠性给出准确量化分析。

技术方案：一种基于caputo型分数阶微分的不确定电路可靠性分析方法，包括以下步骤：

(1)引入不确定liu过程和caputo型分数阶微分算子，依据有限时间区间(0,t)上一阶串联式rc电路系统状态变量xt首次达到崩溃状态的时间τ，建立不确定环境下一阶串联式rc电路系统的分数阶动力学模型；

(2)通过α路的方法求解不确定环境下一阶串联式rc电路系统的分数阶动力学模型，推导出方程解的α路不确定响应

(3)基于不确定分数阶的首达时间定理，给出不确定分数阶一阶串联式rc电路系统的可靠性指标rel；

(4)根据不确定响应和不确定分数阶一阶串联式rc电路系统的可靠性指标rel，带入代入实际电路中的定值，对一阶串联式rc电路系统的可靠性进行分析和优化。

有益效果：本发明提出一种全新的基于首达时间的可靠性准则，并将其应用到基于分数阶微分理论和不确定理论建立的一阶串联式rc电路系统模型中，从而得到一种基于caputo型分数阶微分的不确定电路可靠性分析方法，该方法量化了系统在规定的到期时间t后才达到崩溃状态阈值l的信度，使一阶串联式rc电路系统的可靠性得到更为准确的分析。本发明广泛地适用于非理性情况下的一阶串联式rc电路系统，对包括一阶串联式rc电路系统在内的系统都有较好的应用价值。

附图说明

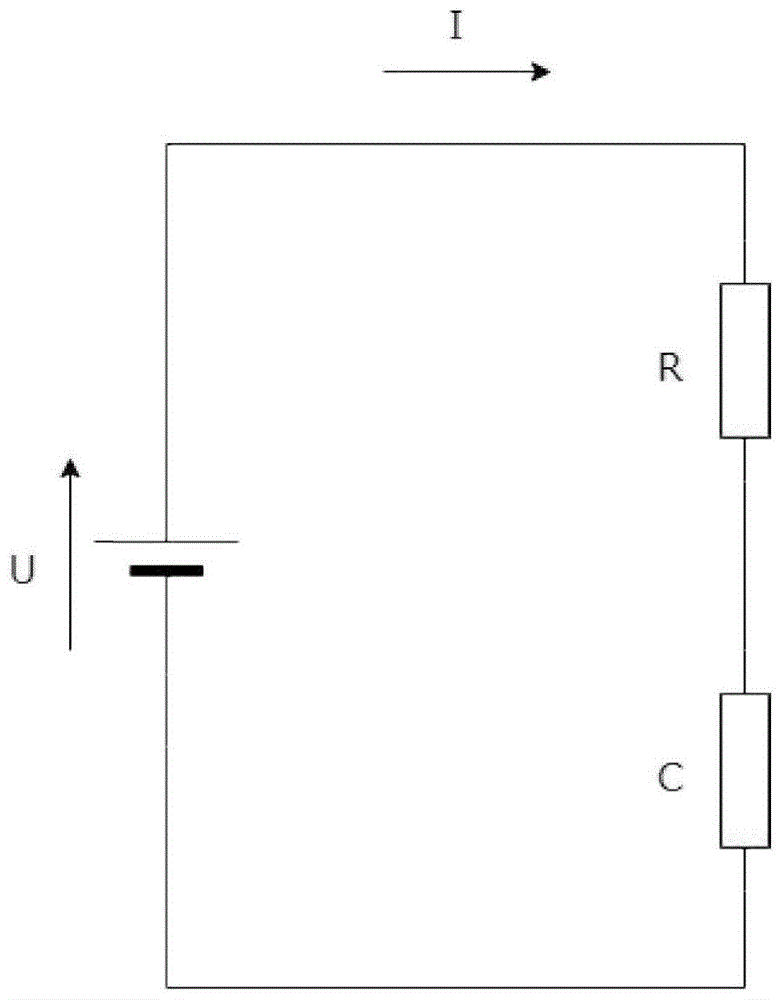
图1为本发明适用的电路示意图；

图2为本发明的可靠性分析方法的流程图；

图3为本发明实施例中x0<l时可靠性与崩溃状态阈值的关系示意图；

图4为本发明实施例中x0<l时可靠性与时间区间上限的关系示意图；

图5为本发明实施例中x0>l时可靠性与崩溃状态阈值的关系示意图；

图6为本发明实施例中x0>l时可靠性与时间区间上限的关系示意图。

具体实施方式

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明的实施方式作进一步的详细描述。

图1示出了本发明适用的电路示意图，如图所示，是一种一阶串联式rc电路。在实践中存在这样的情况，即仅当某指标高于或低于某给定值时，电路模型所在的系统才具有足够的可靠性。例如，在图1所示的电路中，电容电压必须高于特定电压或低于特定电压，电路才能正常工作，这就涉及到指标首次达到给定值的时间和系统在规定时间前达到给定值的信度。本发明提出一种全新的基于首达时间的可靠性准则，并将其应用到基于分数阶微分理论和不确定理论建立的一阶串联式rc电路系统模型中，从而得到一种基于caputo型分数阶微分的不确定电路可靠性分析方法。

参照图2，一种基于caputo型分数阶微分的不确定电路可靠性分析方法，包括如下步骤：

(11)引入不确定liu过程和caputo型分数阶微分算子，构建不确定分数阶全响应状态方程，建立不确定环境下一阶串联式rc电路系统的分数阶动力学模型。

在一个实施例中，对如图1所示的不确定环境下的实际串联式rc电路，使用数字万用表，测得其电阻系数r＝5ω，电容系数c＝1f，电容电压方差σ＝0.5，设分数阶次p＝1.6，电容电压在时间t＝0时的初值x0＝0，有限时间区间为t∈(0,5)，假设崩溃状态阈值l＝4。

基于不确定环境下实际电路的电阻系数r，电容系数c，系统状态变量即电容电压xt，其方差σ，系统外部激励w，得到相应的随时间t变化的整数阶电路方程：

向系统状态变量电容电压xt引入分数阶次p的caputo型分数阶微分算子^cd^p和不确定liu过程ct，依据有限时间区间(0,t)上一阶串联式rc电路系统动态过程xt首次达到崩溃状态l的时间τ，建立不确定环境下一阶串联式rc电路系统的分数阶动力学模型如下：

其中，k为系统状态变量电容电压初值的阶次，n是一个正整数，t为时间区间上限。

本发明采用分数阶微积分这一新的建模工具来刻画电路系统的幂律性现象。不同于仅由函数的局部特征决定的整数阶微积分，分数阶微积分以加权形式积累了函数的全局信息，考虑了过往时刻的系统行为特征，从而有效地保持了系统的记忆性。因此，基于分数阶微积分建立的数学模型可以更准确地描述实际电路系统的动态响应，进一步提高对电路系统的设计、表征和控制能力。

刘宝碇教授于2007年首次引入不确定性理论，以此合理描述不确定事件的信度。在2009年，他对不确定性测度的公理化定义进行了修正，同时提出的还有对应的微分方程，即不确定性微分方程。作为不确定过程的特殊数值特征的首达时间，在2013年由刘宝碇教授初步定义。后来，姚凯在2013年对不确定分布进行了研究，并提出了首达时间的数值方法。同时，首达时间在智能故障诊断、可靠性(风险)分析、运维技术和电力控制等国际自动控制领域的热点问题上得到了广泛的应用。

考虑到实际电路系统中存在的反常现象，与研究过程中的样本数据获取困难，本发明通过引入caputo分数阶微分算子，在不确定环境下对电路系统建模，并基于此提出相应的可靠性指标，足以建立更优越的可靠性分析方法。

(12)通过α路(α-path)的方法，利用mittag-leffler函数，求解不确定环境下一阶串联式rc电路系统的分数阶动力学模型，推导方程解xt的α路不确定响应如下：

其中，y和z为中间运算变量，ek+1表示mittag-leffler函数，σ表示方差，t^k表示时间t的k次方。

(13)基于不确定分数阶的首达时间定理，给出不确定分数阶一阶串联式rc电路系统的可靠性指标rel定义。

本发明通过比较系统状态初始量x0与系统崩溃状态阈值l的大小，确定系统状态变量xt关于时间t是单调递增关系或单调递减关系，基于状态变量xt关于时间t的函数关系以及电路系统在首达时间τ达到崩溃状态，给出相应的系统崩溃的置信度β，从而确定可靠性指标。

在本实施例中，由于x0<l，因此系统状态变量xt关于时间t单调递增，将在首达时间τ达到崩溃状态l。给出可靠性指标定义rel如下，用以衡量系统崩溃的信度：

其中，表示事件发生的不确定信度(一种测度)，τ＝inf{t≥0|xt＝l}。

同时，定义系统崩溃的置信度β如下：

基于不确定分数阶的首达时间定理，对单调递增函数xt有：

其中，u为首达时间的不确定分布函数。

那么，联立(1)、(3)，将定义(1)转化为如下等式：

向上式引入定义式(2)，则有

rel＝1-β,x0<l

(14)根据不确定响应和不确定分数阶一阶串联式rc电路系统的可靠性指标rel，分析和优化一阶串联式rc电路系统的可靠性。

基于步骤(12)中给出的和步骤(13)的rel，推导得到不确定分数阶rc一阶串联式rc电路系统的可靠性指标：

通过代入实例中r、c、p、w、t、l的定值，分析rel关于l和t的灵敏性，依据实际情况，对使rel增减过快的参数范围进行规避，从而实现电路系统可靠性的优化。图3和图4给出了对上述rc电路的可靠性分析进行灵敏性分析的结果。

由图3可以看出，可靠性rel与崩溃状态阈值l成反比，表明该方法与实际情况相吻合。另外，显然地，在l∈(1.5,2.3)的区间上，可靠性指标rel快速降低，在此区间两边，可靠性指标rel的下降趋势明显更加平缓，并最终趋于0。由图示关系可知，本实施例的一阶串联式rc电路系统在实际使用中，应尽量在区间(0,1.5)内选定崩溃状态阈值l，以获得可靠性较高且较稳定的动态系统过程。同时，应避免在区间(2.3,∞)内选择崩溃状态阈值l，防止出现一阶串联式rc电路系统长期可靠性偏低的情况。

由图4可以看出，可靠性rel与时间区间上限t成正比，表明该方法与实际情况相吻合。另外，显然地，在t∈(1.7,2.8)的区间上，可靠性指标rel快速增大，在此区间两边，可靠性指标rel的上升趋势明显更加平缓，并最终趋于1。由图示关系可知，本实施例的一阶串联式rc电路系统在实际使用中，应尽量在区间(2.8,∞)内选定时间区间上限t，以获得可靠性较高且较稳定的动态系统过程。同时，应避免在区间(0,1.7)内选择时间区间上限t，防止出现一阶串联式rc电路系统长期可靠性偏低的情况。

在另一实施例中，对一个如图1所示的不确定环境下的实际串联式rc电路，使用数字万用表，测得其电阻系数r＝4，电容系数c＝2，方差σ＝0.5，分数阶次p＝1.6，状态变量初值x0＝5，有限时间区间为(0,2)，崩溃状态阈值l＝2。对该电路模型的可靠性分析的具体操作如下：

在步骤(21)中，建立不确定环境下一阶串联式rc电路系统的分数阶动力学模型：

在步骤(22)中，求解步骤(21)中建立的不确定分数阶电路模型，通过α路(α-path)方法推导方程解xt的α路不确定响应如下：

其中，

在步骤(23)中，由于x0>l，系统状态变量xt关于时间t单调递减，将在首达时间τ达到崩溃状态l。给出可靠性指标定义rel如下，用以衡量系统崩溃的信度：

其中，表示事件发生的不确定信度(一种测度)，τ＝inf{t≥0|xt＝l}。

同时，定义系统崩溃的置信度β如下：

基于不确定分数阶的首达时间定理，对单调递减函数xt有：

其中，u为首达时间的不确定分布函数。

那么，联立(4)、(6)，将定义(4)转化为如下等式：

向上式引入定义式(5)，则有：

rel＝1-β,x0>l

在步骤(24)中，基于步骤(22)中给出的和步骤(23)推导的rel，推导得到不确定分数阶rc一阶串联式rc电路系统的可靠性指标：

通过代入实例中的定值，分析rel关于l和t的灵敏性，对使rel增减过快的参数范围进行规避，从而实现电路系统可靠性的优化。图5和图6给出了对本实施例中上述rc电路的可靠性分析进行灵敏性分析的结果。

由图5可以看出，可靠性rel与崩溃状态阈值l成正比，表明该方法与实际情况相吻合。另外，显然地，在l∈(2.0,2.4)的区间上，可靠性指标rel快速增大；在此区间两边，可靠性指标rel的上升趋势明显更加平缓，并最终趋于1。由图示关系可知，本案例讨论的一阶串联式rc电路系统在实际使用中，应尽量在区间(2.4,∞)内选定崩溃状态阈值l，以获得可靠性较高且较稳定的动态系统过程。同时，应避免在区间(0,2.0)内选择崩溃状态阈值l，防止出现一阶串联式rc电路系统长期可靠性偏低的情况。

由图6可以看出，可靠性rel与时间区间上限t成正比，表明该方法与实际情况相吻合。另外，显然地，在t∈(2.0,2.3)的区间上，可靠性指标rel快速增大；在此区间两边，可靠性指标rel的上升趋势明显更加平缓，并最终趋于1。由图示关系可知，本案例讨论的一阶串联式rc电路系统在实际使用中，应尽量在区间(2.3,∞)内选定时间区间上限t，以获得可靠性较高且较稳定的动态系统过程。同时，应避免在区间(0,2.0)内选择时间区间上限t，防止出现一阶串联式rc电路系统长期可靠性偏低的情况。

以上，即在针对x0<l和x0>l两种情况下的rc电路模型的分析中，通过引入不确定liu过程和caputo型分数阶微分算子，构建不确定分数阶全响应状态方程，建立不确定环境下一阶串联式rc电路系统的分数阶动力学模型，并通过α路(α-path)的方法求解该模型，最后结合定义的不确定分数阶一阶串联式rc电路系统模型的可靠性指标，依据所定义指标的解析式对现有电路模型完成可靠性分析。利用本发明所提出的一种基于caputo型分数阶微分的不确定电路可靠性分析方法，相比于现有的理想方法，更符合现实情况，同时能满足不同信念程度的用户需求。