一种交通小区协调优化方法与流程

本发明涉及区域交通优化
技术领域：
，尤其是指一种交通小区协调优化方法。
背景技术：
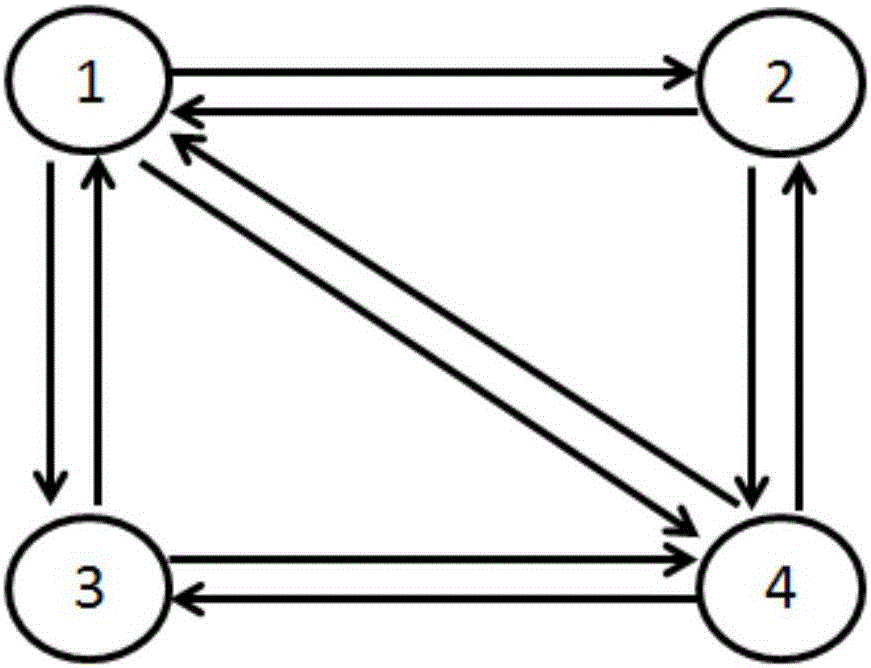
：随着当前城市机动化的迅速发展，道路系统逐渐趋向饱和，交通运转已经“牵一发而动全身”，区域性的交通问题日益突出。因此，对于交通管理与服务而言，也必须保持全局观，从整个道路网络的大局出发，站在宏观角度解决局部的交通瓶颈问题。对于路网系统而言，传统的对于交叉口、路段的研究方法并不完全适应，需要基于整体网络的宏观交通理论与方法。交通流宏观基本图便是可以描述整个网络的交通流状态的的宏观模型，可反映流出道路网车辆数和路网内车辆数之间存在关系。不少学者基于宏观基本图理论，提出各自的协调控制方法。杜曼怡等提出了以基于宏观基本图及反馈门的区域总量动态调控方法，通过区域边界设置的“反馈门”控制网络流入量，将网络车辆总数维持在其合理可行范围内。该方法通过边界交叉口控制，减少进入网络流量，虽然研究网络内的车辆数合理，但转移的流量会增加其他路网的压力，且转移的流量不可控。赵靖等以两个相邻控制子区为对象，考虑各子区自身宏观基本图特征及交通量流入流出关系，在运用博弈论对其相互作用进行描述的基础上，提出了一种以两个子区整体运行效益最大化为目标的博弈控制模型。该模型使相邻子区整体处于最优的运行状态，但在整体路网中，不存在独立的相邻子区，该研究中相邻子区任意一个子区必然还有其它与之相邻的子区。然而该模型并没有验证一个子区与第二个相邻子区的博弈是否影响之前博弈的结果，因此该模型缺乏整体性。技术实现要素：本发明的目的在于克服现有技术的缺点与不足，提出了一种能够快速疏解交通拥堵、行状态均衡交通流、最大化网络运行效率的交通小区协调优化方法，该方法是以小区为控制对象，以宏观基本图为基础，以网络优化模型为核心，输出各小区之间的最优交通流。为实现上述目的，本发明所提供的技术方案为：一种交通小区协调优化方法，包括以下步骤：1)确定所研究的城市路网范围，获取基础资料，包括研究范围内所有道路的通行能力、研究范围内的平均小时交通生成量、到达终点车辆数与驶出路网车辆数的比例；2)将整个交通网络划分为若干个交通控制小区，以小区为网络交通流优化对象，对所研究的城市交通路网进行简化；3)构造网络优化有向图：以小区为节点，以边表示小区之间的道路，将路网抽象为点边组成的有向图；4)绘制宏观基本图4.1)布设检测器，在各个小区边界的出入口布设检测器，收集数据；4.2)根据所收集数据，绘制区域及各个小区宏观基本图，宏观基本图模型的纵坐标为驶出车辆数，单位为辆/分钟，即通过道路驶出小区或网络边界的车辆数与支路到达终点的车辆数之和；横坐标为区域内车辆数，对于整体路网而言，宏观基本图的纵坐标为网络内车辆数，对于小区而言，其宏观基本图的纵坐标为小区内车辆数；5)利用聚类方法将宏观基本图的散点分为上升段、持续段和下降段三类，并分别进行线性拟合；6)以小区之间的流量为决策变量建立网络优化模型，优化目标为输出车辆数最大同时路网利用率较高，约束条件为各节点的最大车辆数和各边的通行能力；7)输入路网当前运行状态下的各节点内车辆数，求解模型，获得边上最佳流量。在步骤2)，交通小区是具有一定交通关联度的交叉口和路段的集合，关联性较大的交叉口划归为同一小区，交通小区划分的方法有：基于谱方法的小区划分方法，基于交通流特性的小区划分方法或交通工程师根据经验进行手动划分。在步骤3)，将小区抽象成节点，将小区之间的连接道路抽象为边，形成由节点与边组成的网络优化有向图；其中节点编号与简化前的小区编号相对应，节点之间是否存在边，及边的方向取决于原网络中两个小区之间是否有相应方向的路段相连，简化后的有向图主要用来描述网络的宏观状态；其中节点的属性包括小区的宏观基本图、区内能容纳最大车辆数；节点对有向图输出的状态变量有小区内的车辆数，进入小区车辆数与驶出小区车辆数；边的属性主要为方向通行能力，边输出的状态变量为各小区间的交通流。在步骤5)，利用聚类方法将每一个小区的宏观基本图的散点分成三类，之后用直线进行分段拟合；设三段拟合函数分别为：f1(n)，f2(n)，f3(n)则:G(n)＝min{f1(n),f2(n),f3(n)}式中：n为网络内车辆数；G(n)为驶出网络车辆数，单位为辆/分钟；在步骤6)，建立网络优化模型，包括以下内容：6.1)确定每个交通小区的最优点根据宏观基本图特性，令持续段和下降段的交点作为网络运行的最优点(nm,gm)，该点表示网络处于驶出流量最大情况下网络内容纳的车辆数最多的状态，该状态的网络运行效率最高，服务车辆数也相对较多；6.2)网络优化模型决策变量为小区之间的交通流，表示第t个研究时段由小区i到小区j的交通量；6.3)网络优化模型的目标为使整体路网的运行状态处于最优水平，即使每个小区的优化后的状态点与最优点的距离之和最小，所以网络优化模型的目标函数为:式中，为小区i在第t个研究时段内的车辆数；为小区i在第t个研究时段内的驶出车辆数；6.4)根据步骤5)对各个小区的宏观基本图进行聚类分段拟合的结果，有：6.5)根据流量守恒原则，有：其中，为小区i在上一个研究时段内的车辆数；为小区i在第t个研究时段内产生的交通量；为小区i在第t个研究时段到小区j的交通量；为第t个研究时段小区i到达终点的车辆数占所有驶出小区车辆数的比例；6.6)网络优化模型的约束条件有：①小区内车辆数不得超过小区能容纳的最大车辆数，即为小区i达到阻塞密度对应小区车辆数，从小区宏观基本图获得；②小区间的交通流应小于边的通行能力，即Cij表示连接小区i和小区j的边的通行能力；③小区间的交通流应大于边的最小交通量，即dij表示小区i到小区j的最小交通量；④进入每个小区的车辆数应小于该小区能接受的最大流量，即为小区i在第t个研究时段内能够接受的最大流量；⑤每个小区的驶出车辆数应小区该小区能够流出的最大流量，即为小区i在第t个研究时段内能够流出的最大流量。在步骤7)，求解模型是以网络状态为输入条件进行求解，解为各小区之间的流量，根据现状路网及其运行状态，确定以下参数：①每个小区的最优点(nm,gm)；②当前状态下，各个小区内的车辆数③当前状态下，各个小区在单位时间内产生的交通量④各个小区到达终点的车辆数占所有驶出小区车辆数的比例⑤各个小区的能容纳的最大车辆数⑥连接小区i和小区j的边的通行能力Cij；边上最小交通量dij,；⑦当前状态下，各个小区能够接受的最大流量及够流出的最大流量对优化模型进行求解，获得即为小区间最优交通流量值。本发明与现有技术相比，具有如下优点与有益效果：1、具有可实施性。本方法提出的小区划分契合目前主流使用的SCATS系统，为SCATS系统子区内部控制提供输输入条件。2、能够快速疏解区域拥堵。本方法在局部区域发生拥堵时，只需输入当前状态参数即可马上求解小区之间的最佳交通流。3、能预防局部拥堵发生。在监控到某小区流量发生变化时，可以及时生成方案，调节该小区运行状态。4、不会增加车辆出行距离。本方法只调节小区状态，不像大多数交通诱导方法使车辆绕行，从而增加车辆出行距离。5、具有先进性。宏观基本图是今年来宏观交通流领域中的研究重点，2007年才被正式提出。提出之后便一直是宏观交通流领域的热点，本方法利用以宏观基本图为基础，建立的网络优化模型具有创新性。附图说明图1a为原始的路网图。图1b为网络优化有向图。图2为驶出网络车辆数与网络内车辆的分布关系图。图3为Vissim仿真界面图。图4为驶出小区车辆数与小区内车辆数关系图(小区1)。图5为驶出小区车辆数与小区内车辆数关系图(小区2)。图6为驶出小区车辆数与小区内车辆数关系图(小区3)。图7为驶出小区车辆数与小区内车辆数关系图(小区4)。图8为网络模型优化结果。图9为网络控制前后驶出网络车辆数分布情况图。图10为网络控制前后进入网络车辆数分布情况图。图11为网络控制前后驶出小区车辆数分布情况图(小区1)。图12为网络控制前后进入小区车辆数分布情况图(小区1)。图13为网络控制前后驶出小区车辆数分布情况图(小区2)。图14为网络控制前后进入小区车辆数分布情况图(小区2)。图15为网络控制前后驶出小区车辆数分布情况图(小区3)。图16为网络控制前后进入小区车辆数分布情况图(小区3)。图17为网络控制前后驶出小区车辆数分布情况图(小区4)。图18为网络控制前后进入小区车辆数分布情况图(小区4)。图19为本发明的交通小区协调优化方法流程图。具体实施方式下面结合具体实施例对本发明作进一步说明。如图19所示，本发明所述的交通小区协调优化方法，包括以下步骤：1)确定所研究的城市路网范围，获取基础资料，包括研究范围内所有道路的通行能力、研究范围内的平均小时交通生成量、到达终点车辆数与驶出路网车辆数的比例等。2)将整个交通网络划分为若干个交通控制小区，以小区为网络交通流优化对象，对所研究的城市交通路网进行简化。3)构造网络优化有向图：以小区为节点，以边表示小区之间的道路，将路网抽象为点边组成的有向图。4)绘制宏观基本图4.1)布设检测器，在各个小区边界的出入口布设检测器，收集数据。4.2)根据所收集数据，绘制区域及各个小区宏观基本图。宏观基本图模型的纵坐标为驶出车辆数，单位为辆/分钟，即通过道路驶出小区或网络边界的车辆数与支路到达终点的车辆数之和；横坐标为区域内车辆数，对于整体路网而言，宏观基本图的纵坐标为网络内车辆数，对于小区而言，其宏观基本图的纵坐标为小区内车辆数。本专利所使用的宏观基本图应满足一定要求:1)宏观基本图的点分布较为集中，呈现一定的规律性。2)宏观基本图应完整，随横坐标的增大，应包含上升、持续和下降三段。满足本发明使用的宏观基本图可参考图2。5)利用聚类方法将宏观基本图的散点分为上升段、持续段和下降段三类，并分别进行线性拟合。6)以小区之间的流量为决策变量建立网络优化模型，优化目标为输出车辆数最大同时路网利用率较高，约束条件为各节点的最大车辆数和各边的通行能力。7)输入路网当前运行状态下的各节点内车辆数，求解模型，获得边上最佳流量。在步骤2)，交通小区是具有一定交通关联度的交叉口和路段的集合，一般的，关联性较大的交叉口划归为同一小区。交通小区划分的常用方法有：基于谱方法的小区划分方法，基于交通流特性的小区划分方法或交通工程师根据经验进行手动划分等。在步骤3)，将小区抽象成节点，将小区之间的连接道路抽象为边，形成由节点与边组成的网络优化有向图，如图1b所示。其中，节点编号与简化前的小区编号相对应，如图1a所示，节点之间是否存在边，及边的方向取决于原网络中两个小区之间是否有相应方向的路段相连。简化后的有向图主要用来描述网络的宏观状态，其中节点的属性包括小区的宏观基本图，区内能容纳最大车辆数等，节点对有向图输出的状态变量有小区内的车辆数，进入小区车辆数与驶出小区车辆数；边的属性主要为方向通行能力，边输出的状态变量为，各小区间的交通流。在步骤5)，由于本发明使用的宏观基本图具有明显三阶段特征，利用聚类方法将每一个小区的宏观基本图的散点分成三类，之后用直线进行分段拟合。以图2为例，对其进行聚类分析后，分三段分别进行拟合，设三段拟合函数分别为：f1(n)，f2(n)，f3(n)则:G(n)＝min{f1(n),f2(n),f3(n)}式中：n为网络内车辆数；G(n)为驶出网络车辆数，单位为辆/分钟。在步骤6)，建立网络优化模型，包括以下内容：6.1)确定每个交通小区的最优点根据宏观基本图特性，令持续段和下降段的交点作为网络运行的最优点(nm,gm)。该点表示网络处于驶出流量最大情况下网络内容纳的车辆数最多的状态，该状态的网络运行效率最高，服务车辆数也相对较多。6.2)网络优化模型决策变量为小区之间的交通流，表示第t个研究时段由小区i到小区j的交通量。6.3)网络优化模型的目标为使整体路网的运行状态处于最优水平，即使每个小区的优化后的状态点与最优点的距离之和最小。所以网络优化模型的目标函数为:式中，为小区i在第t个研究时段内的车辆数；为小区i在第t个研究时段内的驶出车辆数。6.4)根据步骤5)对各个小区的宏观基本图进行聚类分段拟合的结果，有：6.5)根据流量守恒原则，有：其中，为小区i在上一个研究时段内的车辆数；为小区i在第t个研究时段内产生的交通量；为小区i在第t个研究时段到小区j的交通量；为第t个研究时段小区i到达终点的车辆数占所有驶出小区车辆数的比例。6.6)网络优化模型的约束条件有：①小区内车辆数不得超过小区能容纳的最大车辆数，即为小区i达到阻塞密度对应小区车辆数，可从小区宏观基本图获得；②小区间的交通流应小于边的通行能力，即Cij表示连接小区i和小区j的边的通行能力；③小区间的交通流应大于边的最小交通量，即dij表示小区i到小区j的最小交通量；④进入每个小区的车辆数应小于该小区能接受的最大流量，即为小区i在第t个研究时段内能够接受的最大流量；⑤每个小区的驶出车辆数应小区该小区能够流出的最大流量，即为小区i在第t个研究时段内能够流出的最大流量。在步骤7)，求解模型是以网络状态为输入条件进行求解，解为各小区之间的流量，根据现状路网及其运行状态，确定以下参数：①每个小区的最优点(nm,gm)；②当前状态下，各个小区内的车辆数③当前状态下，各个小区在单位时间内产生的交通量④各个小区到达终点的车辆数占所有驶出小区车辆数的比例⑤各个小区的能容纳的最大车辆数⑥连接小区i和小区j的边的通行能力Cij；边上最小交通量dij,；⑦当前状态下，各个小区能够接受的最大流量及够流出的最大流量对优化模型进行求解，获得即为小区间最优交通流量值。可应用梯度投影法，牛顿法，交替方向乘子法等。案例分析选取与图2相似的简单路网，利用Vissim仿真软件对网络优化模型的使用进行演示。所选取网络东西向长度300余米，南北向长度2000余米，共有十字交叉口16个。丁字交叉口2个，五路交叉口2个。路段为单向两车道，交叉口拓宽为3车道。十字交叉口为四相位控制，丁字交叉口为三相位控制，五路交叉口为五相位控制。并在各路段设置出入口，车辆通过出入口进入网络或到达终点。Vissim仿真界面如图3所示。利用Vissim进行数次独立仿真可获得各个小区的宏观基本图，即驶出小区车辆数与小区内车辆数的关系，如图4-图7所示。各小区宏观基本图的拟合函数试分别为：小区1的拟合函数为：G1(n)＝Min{22.105n+1177.2,13000,24550-4.4017n}小区2的拟合函数为：G2(n)＝Min{17.701n+1707.5,10050,29123-5.381n}小区3的拟合函数为：G3(n)＝Min{16.366n+824.72,8000,11127-2.632n}小区4的拟合函数为：G4(n)＝Min{23.477n+1083.8,9600,18671.6-3.607n}由各个小区的宏观基本图可以确定各小区的最优点分别为(2500，13000)，(2800，10050)，(2000，8000)，(670，9600)。当网络运行处于不均衡状态时，部分小区处于开始拥堵状态，而其他小区处于流量较低状态时，网络标优化模型可以通过调节小区之间的流量，调整网络运行状态。在不均衡状态中提取优化模型需要的参数，如下表所示。表格1网络优化模型的参数利用梯度法可以求解出模型的解，最优值唯一，最优解不唯一。最优值见下表。表格2优化后状态参数优化后状态小区1小区2小区3小区4小区驶出车辆数130001005076649660小区内车辆数250028001316670取其中一组解验证模型的有效性，各小区之间的最佳交通量如图8所示。根据网络优化结果明确小区层的优化目标，确定小区之间的协调路径。之后将小区之间的流量作为下层生成各个小区交叉口信号配时方案过程中的约束条件。其次在不改变仿真的需求的前提下，将小区现有各方向输出的流量与优化结果进行比较，逐步通过信号配时调整各方向输出的交通量，直至接近网络层的优化结果。最后仿真对比结果如下图所示。从网络控制前后的对比图9-图18可以看出，以网络优化模型结果为指导约束的网络控制对于改变网络运行状态具有显著效果。小区1和小区3在网络控制后的驶出车辆数与进入车辆数都高于网络控制前，小区3在较长时间后任处于较平稳的状态。网络控制改善了小区1和小区3的交通状态，缓解了这两个小区的交通拥堵情况，进而改善路整个网络的运行状态，提高了网络运行效益。以上所述实施例只为本发明之较佳实施例，并非以此限制本发明的实施范围，故凡依本发明之形状、原理所作的变化，均应涵盖在本发明的保护范围内。当前第1页1 2 3