计及奇异值的低频振荡信号参数辨识模型及其参数辨识方法与流程

本发明涉及一种计及奇异值的低频振荡信号模型参数辨识方法，属于信号分析与参数辨识技术领域。

背景技术：

电力系统安全稳定问题与低频振荡信号之间存在着密切联系，低频振荡信号包含着电力系统运行态势信息。因此，如何通过监测和分析手段提取低频振荡信号所表征的信息，适时采取合适的举措，对于保证电力系统安全运行意义重大。

近年来，众多学者围绕电力系统低频振荡信号模态识别，模型参数辨识开展了深入而广泛的研究。针对低频振荡信号模型参数辨识问题，提出了许多有效方法，主要包括快速傅里叶变换(fastfouriertransform,fft)、小波算法、prony算法和扩展卡尔曼滤波算法(extendedkalmanfilter,ekf)等。fft参数辨识方法精度会受到数据窗限制，无法有效反映振荡信号的阻尼特性；基于小波算法的低频振荡信号参数辨识方法能够体现信号时变特性，但存在小波基难选取的问题；prony算法比较简单方便，但其对噪声敏感性大。ekf方法具有在线辨识的特点，而且计算占用内存低，效率高，应用较为广泛。不过，需要指出的是上述这些方法，均未考虑由脉冲噪声等引起奇异值，无法实现此种情形下的低频振荡信号参数准确辨识。

技术实现要素：

发明目的：为了克服现存方法的不足，提高低频振荡信号模型参数辨识方法的鲁棒性和辨识精度，本发明设计一种计及奇异值的低频振荡信号参数辨识模型及其参数辨识方法，该方法通过对奇异值检测、降低权重，并利用迭代最小二乘法寻优，从而避免奇异值所带来的影响，有效改善低频振荡信号模型参数辨识效果。

本发明所采用的技术方案为：一种计及奇异值的低频振荡信号参数辨识模型，建立状态变量分量中包含电力系统低频振荡信号模型待估参数的状态空间模型；

该电力系统低频振荡信号由n个指数衰减的振荡波信号组成：

式中，λi,wi,δi,φi分别为幅值，频率，衰减因子，初始相位；n(t)是一个零均值的白噪声；

定义4n个状态变量为如下形式：

x4i-1,k＝wi(4)

x4i,k＝δi(5)

式中，下标i表示构成低频振荡信号的第i个衰减的振荡波信号，k代表时刻，fs代表采样频率，根据上式，得到k+1时刻的状态分量：

x4i-1,k+1＝x4i-1,k+ω4i-1,k(8)

x4i,k+1＝x4i,k+ω4i,k(9)

式中，ω4i-j,k(i＝1…n,j＝0…3)为k时刻均值为零，协方差矩阵为wk的高斯白噪声；

量测值的输出方程为：

式中，η2i-1＝cos(φi)，η2i＝-sin(φi)，nk为均值为零，协方差矩阵为rk的高斯白噪声。

本发明还提出了基于上述的参数辨识模型的一种参数辨识方法，包括以下步骤：

s1：获取状态变量分量中包含模型参数的状态空间模型；

s2：初始k＝0时刻的参数估计初始值参数估计误差协方差∑0|0，噪声满足的协方差矩阵wk和rk初始值分别为w0和r0，参数辨识最大时刻s；

s3：计算k时刻的参数预测值

式中，f(·)对应低频振荡信号状态方程中非线性系统函数，表示k-1时刻参数估计值；

s4：计算k时刻的参数预测误差协方差∑k|k-1，计算公式如下：

式中，表示函数f(·)在处的雅克比矩阵，∑k-1|k-1为k-1时刻的估计误差协方差；

s5：结合参数预测值和量测值zk，建立线性批处理回归模型，增加低频振荡信号参数辨识的量测冗余量：

式中，hk表示k时刻量测输出矩阵，i为单位矩阵，xk表示k时刻参数真实值，ek～n(0,rk)为符合高斯分布的系统噪声序列，δk|k-1为参数预测值与参数真实值xk的差值；

所满足的协方差矩阵为

lk式中可以通过柯列斯基分解获取；

s6：采用鲁棒投影统计方法，求取数据点h在所有可能向量u的投影值，用以检测步骤(5)线性回归模型中的奇异值；

式中，psi表示第i行对应的投影值，上标(·)^t表示矩阵转置，medk(·)为求取中值的运算，设定判定阈值d，若psi²＞d²，则判定该行为奇异值，根据该行为奇异值，降低该行量测值对应权重即

s7：对s5中的线性回归模型进行白噪化处理：

yk＝akxk+ηk(18)

式中，

s8：迭代最小二乘初始权矩阵为其中q(rsi)＝ψ(rsi)/rsi，ψ(·)表示的函数为：

式中，c为阈值，参数rsi计算方法为

式中，yk(i)表示k时刻量测值的第i行，ai为输出矩阵ak第i行；

s9：利用迭代最小二乘法求解s7，获取低频振荡参数辨识结果；

s10：计算k时刻的估计误差协方差∑k|k：

式中，

s11：依据时间序列进行低频振荡模型参数辨识，直至k+1＞s时迭代停止，输出参数辨识结果。

所述s9中的迭代最小二乘法，计算方法为：

式中为k时刻第v次最小二乘寻优迭代结果，q^(v)为第v次迭代的最小二乘权矩阵。

有益效果：本发明与现有技术相比，本发明的方法通过对奇异值的检测、降低权重等，并利用迭代最小二乘法寻优，从而避免奇异值所带来的影响，有效改善低频振荡信号模型参数辨识效果。

附图说明

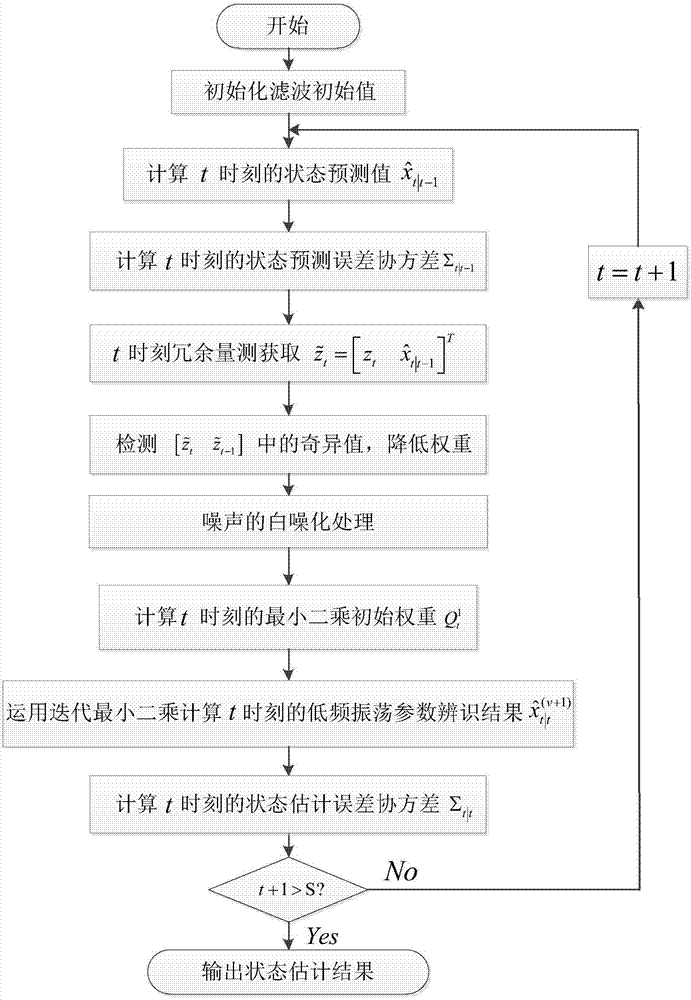
图1为本发明实施例的方法流程图；

图2为实施例含奇异值的低频振荡输入信号；

图3为采用ekf方法对实施例低频振荡输入信号参数辨识结果；

图4为采用本发明方法对实施例低频振荡输入信号参数辨识结果；

图5为采用本发明方法对实施例低频振荡信号参数辨识的绝对误差结果。

具体实施方式

下面结合附图和实施例进一步阐述本发明。

低频振荡模态参数辨识建模

电力系统低频振荡信号由多个指数衰减的振荡波信号组成，即：

式中，λi,wi,δi,φi分别为幅值，频率，衰减因子，初始相位；n(t)是一个零均值的白噪声。

考虑由n个指数衰减的振荡波信号组成的电力系统低频振荡信号，定义4n个状态变量为如下形式：

x4i-1,k＝wi(4)

x4i,k＝δi(5)

式中，下标i表示构成低频振荡信号的第i个衰减的振荡波信号，k代表时刻，fs代表采样频率，根据上式，进一步推导则可得到k+1时刻的状态分量：

x4i-1,k+1＝x4i-1,k+ω4i-1,k(8)

x4i,k+1＝x4i,k+ω4i,k(9)

式中ω4i-j,k(i＝1…n,j＝0…3)为k时刻均值为零，协方差矩阵为wk的高斯白噪声。

量测值的输出方程为：

式中，η2i-1＝cos(φi)，η2i＝-sin(φi)，nk为均值为零，协方差矩阵为rk的高斯白噪声。

至此，状态变量分量中包含电力系统低频振荡信号模型待估参数的状态空间模型已经建立。

如图1所示，运用本发明方法对实施例低频振荡信号模型进行参数辨识，其包含如下步骤：

s1：获取状态变量分量中包含模型参数的状态空间模型；

s2：初始化低频振荡模型参数辨识方法的初始值，如k＝0时刻的参数估计初始值参数估计误差协方差∑0|0，噪声协方差矩阵wk和rk的初始值分别为w0和r0，参数辨识最大时刻s；

s3：计算k时刻的参数预测值计算公式如下：

式中，表示t-1时刻参数估计值，f(·)对应低频振荡信号状态方程中非线性系统函数为如下形式

x4i-1,k+1＝x4i-1,k+ω4i-1,k

x4i,k+1＝x4i,k+ω4i,k

式中，ω4i-j,k(i＝1…n,j＝0…3)为k时刻均值为零，协方差为wk的高斯白噪声；

s4：计算k时刻的参数预测误差协方差∑k|k-1，计算公式如下：

式中，表示函数f(·)在处的雅克比矩阵，∑k-1|k-1为k-1时刻的估计误差协方差；

s5：结合参数预测值和量测值zk，建立线性批处理回归模型，增加低频振荡信号参数辨识的量测冗余量：具体形式如下：

式中hk表示k时刻量测输出矩阵，i为单位矩阵，xk表示k时刻参数真实值，ek～n(0,rk)为符合高斯分布的系统噪声序列，δk|k-1为参数预测值与参数真实值xk差值。该表达式可进一步对应表示为

式中，hk表示k时刻量测输出矩阵，i为单位矩阵，xk表示k时刻参数真实值，ek～n(0,rk)为符合高斯分布的系统噪声序列，δk|k-1为参数真值与预测值xk的差值；

所满足的协方差矩阵为

lk式中可以通过柯列斯基分解获取。

s6：采用鲁棒投影统计方法，求取数据点h在所有可能向量u的投影值，用以检测s5中线性回归模型中的奇异值，其原理如下：

式中，psi表示第i行对应的投影值，上标(·)^t表示矩阵转置，medk(·)为求取中值的运算。设定判定阈值d＝1.5，若则判定该行为奇异值，为了克服其对参数估计的影响，需降低该行量测值对应权重即

s7：对s5中的线性回归模型进行白噪化处理，两端同时乘以即

进一步整理，表示为如下形式

yk＝akxk+ηk(18)

式中

s8：迭代最小二乘初始权矩阵其中q(rsi)＝ψ(rsi)/rsi，ψ(·)表示的函数为：

c＝1.5为阈值(一般取1.5)，参数rsi计算方法为：

式中yk(i)表示k时刻量测值的第i行，ai为输出矩阵ak第i行。

s9：利用迭代最小二乘法求解步骤(7)中的方程，获取低频振荡参数辨识，其计算方法为

式中为k时刻第v次最小二乘寻优迭代结果，q^(v)为第v次迭代的最小二乘权矩阵。

s10：计算k时刻的估计误差协方差∑k|k，计算公式如下

式中

s11：按照(3)-(10)步骤依据时间序列进行低频振荡模型参数辨识，直至k+1＞s时迭代停止，输出参数辨识结果。

实施例：

为了验证本发明方法的有效性和实用性，采用如下电力系统低频振荡模型参数辨识分析常用的一个测试算例，该低频振荡信号的数学表达式为：

y1(t)＝e^-0.012tsin(0.5t)+nt0≤t≤400

该低频振荡信号的频率真实值w＝0.5，阻尼因子真实值为δ＝0.012，在测试中采样时刻t＝k(k＝1,2…400)，nt是高斯白噪声。运用本发明方法进行低频振荡模型参数辨识时，设定最大辨识迭代时刻s＝400，参数辨识初始值设定为参数估计协方差矩阵、系统噪声和量测噪声满足的协防差矩阵初始值分别为：

假设该低频振荡信号的量测值在t＝30,36时刻受到脉冲噪声的影响(即实施例低频振荡输入信号，如图2所示)，即：

n30＝-10，n36＝-10。

对图2含奇异值的低频振荡测试信号进行模型参数辨识分析，分别采用ekf(其所需的相关参数值和本发明方法的参数初值相同)，以及本发明方法进行模态参数辨识。ekf方法对实施例低频振荡信号参数辨识结果如图3所示，本发明方法对实施例低频振荡信号参数辨识结果如图4所示。图5进一步给出了本发明方法参数辨识结果与参数真实值之间的绝对误差值。从图3和图4可以看出，在含奇异值情形下，ekf方法无法收敛于真实值，辨识结果无意义；而本发明所提方法能够有效抑制奇异值所带来的影响，实现低频振荡信号参数准确辨识，表明本发明较ekf方法具有更强的鲁棒性。从图5参数辨识误差可进一步看出，本发明方法具有较高的辨识精度和收敛性能。

基于上述参数辨识结果分析可知，本发明提出的计及奇异值的低频振荡信号模型参数辨识方法能够有效抑制并减弱奇异值带来的辨识误差，具有更强的鲁棒性。