一种混沌背景下弱谐波信号的检测方法与流程

本发明属于混沌信号检测技术领域，特别涉及一种混沌背景下弱谐波信号的检测方法。

背景技术：

混沌背景中的弱信号检测是当前研究的热点之一，受到广泛关注。研究表明，很多工程问题都可以归结为强混沌背景中的弱信号检测的问题，例如机械震荡中的异常信号检测(见文献“B.Li,P.L.Zhang,Z.J.Wang,S.S.Mi,and P.Y.Liu.Morphological covering based generalized dimension for gear fault diagnosis.Nonlinear Dynamics 67,no.4(2012):2561-2571.”)、混沌通信系统安全性能的考察、海洋杂波中的微弱目标信号检测(见文献“J.Hu,W.W.Tung,and J.B.Gao.Detection of low observable targets within sea clutter by structure function based multifractal analysis.Antennas and Propagation,IEEE Transactions on.2006Jan；54(1):136-43.”)等，在这些工程问题中，背景杂波可视作强的混沌信号，目标信号往往非常微弱。因此，强混沌背景中的微弱目标信号检测问题的研究具有很强的工程实际意义。

目前强混沌背景下的弱谐波信号检测方法主要分两大类：基于Takens相空间重建的检测方法和基于最优滤波的检测方法。基于Takens相空间重建的检测方法主要是利用混沌相空间的几何结构与目标信号不同的特点进行检测，其中，神经网络方法最受关注(见文献“行鸿彦,徐伟.混沌背景中微弱信号检测的神经网络方法[J].物理学报,2007,56(7):3771-3776”)。神经网络方法是基于神经网络训练得到混沌背景信号的一步预测模型，通过原信号减去重构的混沌背景得到一步预测误差来实现弱谐波信号的检测。然而，由于混沌系统本身是一个耗散系统，因此上述方法对混沌背景进行预测重构时容易出现预测误差，造成目标信号检测时出现较大的偏差。针对上述问题，文献“J.F.Hu,Y.X.Zhang,H.Y.Li,and W.Xia,Harmonic Signal Detection Method from Strong Chaotic Background Based on Optimal Filter.Acta Physica Sinica,64,220504(2015)”提出了最优滤波方法，该方法根据混沌背景的二阶统计特性不变的特点，把弱信号检测问题转化成频域上的最优滤波器的设计问题。然而，该方法涉及到矩阵求逆计算，可能存在算法不稳定的问题；同时，该方法运算量较大，限制了该算法的工程应用。

技术实现要素：

针对上述存在问题或不足，为解决算法计算复杂度高，检测性能低，算法不稳定的技术问题，本发明提供了一种基于混沌背景下的弱谐波信号检测方法。

该基于混沌背景下的弱谐波信号检测方法，包括以下步骤：

步骤1、构建数据矩阵，将强混沌背景下的微弱谐波信号检测问题转化为最优化问题。

随机选取N段只含强混沌背景噪声的信号作为参考序列，即y_z作为参考单元，用来估计混沌干扰协方差矩阵，N为偶数；将y_x放置在检测单元。检测单元和参考单元共同作为数据矩阵的行向量，则该矩阵一共有N+1行单元数据。其中，检测单元的频域数据y＝[y₁,y₂,...,y_M]^T，参考单元数据y_i,(i＝1,2,...,N)为y_i＝[y_i1,y_i2,...,y_iM]^T。M为信号的采样点数，即频率通道数。数据矩阵的格式如图1所示。

所述待检测序列(Sequence to be Detected)：y_x(n)＝c_x(n)+s(n)，其中y_x(n)是待检测序列，包含混沌信号c_x(n)和谐波信号s(n)。通常混沌信号非常强，而谐波信号很弱，导致检测很困难。

所述参考序列(Reference Sequence)：y_z(n)＝c_z(n)，不含谐波信号，只包含混沌信号c_z(n)。

步骤2、计算混沌干扰协方差矩阵

步骤3、计算频率通道为ω_l(l＝1,…,M)的信号频率导向向量s(ω_l)

步骤4、建立状态方程和量测方程：

状态方程为：

w(n)＝αw(n-1)+v_s(n) (3)

其中，α≤1是一个常数，v_s(n)是过程噪声向量，设为零均值高斯白噪声，其协方差矩阵为：I是单位矩阵，下标s表示对应于状态转移方程，w(n)表示滤波器递归权向量状态n时的值。

量测方程为：

将式(4)所示量测方程写为矩阵形式为：

z＝h(w(n))+v_m(n) (5)

其中，h₂(w(n))＝ε²w^H(n)w(n)-w^H(n)ss^Hw(n)+w^H(n)s+s^Hw(n)，ε为常数取值在10^-3～10^-5的数量级，s是信号导向向量集，v₁(n)是剩余误差，v₂(n)是约束误差；最小化v₁(n)使滤波器输出达到最小，最小化v₂(n)保证待检测频率信号无失真的输出，v₁(n)和v₂(n)建模为两个独立的零均值高斯白噪声，其协方差矩阵为：

其中，的取值与滤波器输出相当，而取值满足约束条件，其典型值是10^-12。

步骤5、计算Jacobin矩阵H_w(n,w(n))和两个Hessian矩阵

Jacobin矩阵H_w(n,w(n))为：

分别为：

步骤6、设递归权向量w的初始化权向量估计为w(0)，其相应的初始化协方差矩阵为P(0|0)。则权向量估计的更新为

步骤7、依次计算预测量测矩阵滤波器增益权向量G(n)，新息协方差矩阵S(n)，量测预测协方差矩阵P(n|n-1)和更新协方差向量P(n|n)。

P(n|n-1)＝α²P(n-1|n-1)+Q (14)

P(n|n)＝P(n|n-1)-G(n)S(n)G^H(n) (15)

将式(11)～式(15)代入式(10)进行反复迭代直至收敛，此时得出的滤波器权向量为最优滤波器权向量

步骤8、计算输出信噪比：

依据式(16)分别计算各个频率通道信号的输出SINR，根据输出SINR的能量来检测出目标信号所在的频率。

本发明基于扩展卡尔曼extended Kalman filter(EKF)，根据混沌背景的二阶统计特性不变的特点，首先把弱谐波信号检测问题转化为最小方差检测问题，在此基础上建立量测方程和状态方程，从而避开矩阵求逆，并用EKF方法迭代计算出滤波器权值，在滤波器权值的基础上计算出信号输出信干噪比SINR，根据信号输出信干噪比来检测出弱谐波信号。

通过设计一个可以让目标信号无失真通过，杂波信号通过遭到抑制的滤波器。滤波器输出时，目标信号能量远大于杂波信号能量，能量将在目标信号频率处发生汇聚，根据频率-输出信干噪比图找出能量最高的点从而判断目标信号存在状态，完成对目标信号的检测。

依据混沌信号具有稳定的二阶统计特性，用没有弱谐波信号的混沌背景信号做参考信号，设计一个滤波器，保留弱谐波信号的同时将强混沌背景信号过滤掉，从而检测出该弱谐波信号：

其中，w是设计的滤波器的系数，s是期望的信号导向矢量。表示滤波器把强的混沌背景信号给过滤掉，w^Hs＝1表示弱谐波信号经过该滤波器后不失真。

||wc||²＝w^HRw,其中，R表示混沌背景信号的二阶统计特性。由于混沌信号的二阶统计特性不变，使用只含混沌背景信号的参考信号来估计待检测信号中的混沌背景信号。

在式(17)中，约束条件w^Hs＝1的意义在于保证弱谐波信号不失真传输。在实际工程应用中，期望的信号导向矢量s和真实信号导向矢量d存在着一定程度上的误差：

d＝s+δ (18)

其中，δ为检测所用的导向矢量s与真实导向矢量d之间的偏差，||δ||≤ε。

式(18)说明，真实导向矢量d是包含在检测时所用的期望导向矢量s的一个邻域内，定义如下：

式(19)中当e＝δ时，u＝d。由于δ未知，d可能为中的任意一个向量，所以我们假设这样一个约束条件：对于包含在中的所有向量，滤波器的输出的绝对值都不小于1，即：

采用式(20)所示约束条件，则式(17)所描述的优化问题变为如下形式：

对于式(21)所描述的优化问题，由于真实导向矢量d包含在中，所以不等式约束条件保证了待检测的目标信号通过滤波器后不会衰减。但该约束条件仅使得该优化问题是非线性、非凸的。因此，接下来我们将继续对约束条件进行推导。首先，式(21)所述优化问题的约束条件等价于下式：

利用Cauchy-Schwarz不等式以及条件||e||≤ε能够得到：

|w^Hs+w^He|≥|w^Hs|-|w^He|≥|w^Hs|-ε||w|| (23)

当ε足够小，即|w^Hs|＞ε||w||时有：

|w^Hs+w^He|＝|w^Hs|-ε||w|| (24)

所以，式(24)可以转换为：

进而式(21)所示的优化问题可以进一步表示为：

式(21)将式(17)的问题进行了简化，并转化成一个凸优化问题。对于最优滤波器的目标方程w^HRw，将其表示为最优滤波器输出与0信号之间的均方误差(mean square error,MSE)，即：

MSE＝E[|0-y^Hw(n)|²]＝w^HRw (27)

于是，进一步将原最优化问题式(17)转化为以下最优化问题：

其中，限制条件h(w(n))＝1表述为：

h₂(w(n))＝ε²w^H(n)w(n)-w^H(n)ss^Hw(n)+w^H(n)s+s^Hw(n)＝1 (29)

由于优化问题是非线性的，所以采用扩展卡尔曼进行最优权向量的求解，根据式(28)和式(29)，推导出其状态方程(3)和量测方程(5)。

有了状态方程和测量方程，再利用卡尔曼滤波器求解权向量w。因为量测方程是非线性的，所以下面采用二阶EKF，将h(·)在w(n)处进行二阶泰勒级数展开，得到Jacobin矩阵H_w(n,w(n))。

对H_w(n,w(n))分别求一阶导数和二阶导数，得到两个Hessian矩阵

按照步骤6，步骤7进行反复迭代，以更新滤波器权值直至其收敛于最优滤波器权值。获得最优滤波器权值后，由步骤8计算出滤波器的输出SINR。根据输出SINR，从混沌背景中实现弱谐波信号的检测。由上文的推导过程可知，式(7)Jacobin矩阵的计算复杂度为O(M²)；式(10)权向量迭代的计算复杂度为O(M)；式(11)预测矩阵的计算复杂度为O(M²)；式(12)滤波器权向量G(n)增益为O(M²)。

式(13)的新息协方差矩阵S(n)计算复杂度为O(M²)，是对传统新息协方差矩阵的优化。

式(15)的更新协方差向量P(n|n)计算复杂度为O(M²)，是对传统更新协方差向量的优化。传统的更新协方差向量为：

其计算复杂度为O(M³)。优化后，可降低算法整体的计算复杂度。

由此可得，本发明所提的扩展卡尔曼滤波器的计算复杂度为O(M²)。而根据文献“S.A.Vorobyov,A.Gershman,and Z.Q.Luo,“Robust adaptive beamforming using worst-case performance optimization:A solution to the signal mismatch problem,”IEEE Trans.Signal Process.,vol.51,no.2,pp.313–324,Feb.2003”的推导，SOCP的计算复杂度为O(M³)。因此，本文所提的扩展卡尔曼滤波器的快速算法计算复杂度优于SOCP的计算复杂度。

综上所述，本发明具有算法稳健，计算复杂度低，检测性能好的技术效果。

附图说明

图1是本发明的数据矩阵格式图；

图2-a为神经网络方法检测结果；图2-b为SOCP方法检测结果；图2-c为本实施例检测结果；

图3是实施例与现有二种检测方法在不同输入信干噪比下的输出信干噪比图。

具体实施方式

下面结合附图和实施例对本发明做进一步的阐述。

这里以Lorenz系统产生混沌背景信号，该系统的非线性状态方程为：

其中σ＝10，r＝28，b＝8/3，步长为0.01，初始值x₀＝y₀＝z₀＝0.1。

在产生的Lorenz混沌信号中，随机选取5段长度为2000的混沌背景信号数据作为本实验的强混沌背景，往第1段数据中加入弱谐波信号作为检测单元的信号，其余4段数据作为只含混沌背景信号的参考单元信号。谐波信号用s(n)＝αe^j2πfn来表示，其中固定谐波信号的归一化频率f＝0.06Hz，谐波信号的幅值|α|＝0.05。

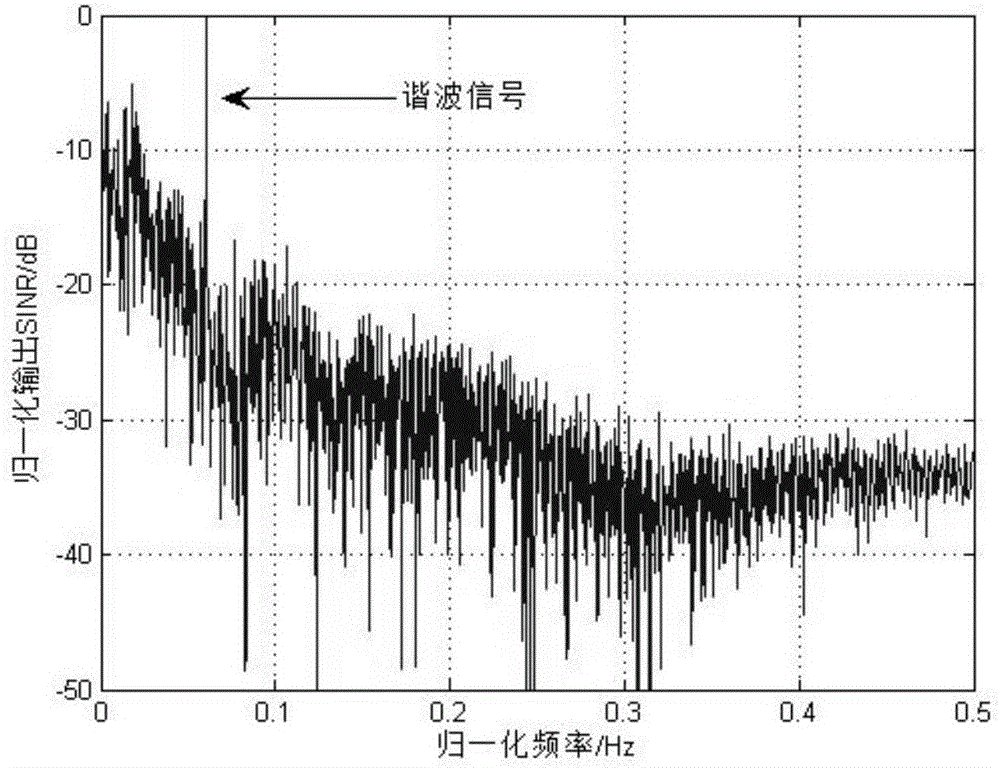
分别采用神经网络算法，基于SOCP的最优滤波器算法和本文所提的EKF快速算法分别进行检测，检测结果如图2所示：

图2是在SINR＝-47.01dB(α＝0.05)时，采用神经网络算法，基于SOCP的最优滤波器算法和本文所提的EKF快速算法在强混沌背景下的信号检测结果。图2(a)中，采用神经网络算法，谐波信号只比最大旁瓣高6dB。而图2(b)和图2(c)中，采用基于SOCP的最优滤波器算法和本文所提EKF快速算法，在f＝0.06Hz处，谐波信号比最大旁瓣高12dB。由图1可看出，本文所提EKF 快速算法性能优于神经网络算法，和基于SOCP的最优滤波器算法性能相当。

定义输出信干噪比为：主瓣和最大旁瓣的比值。图3给出神经网络算法，基于SOCP最优滤波器算法和本文所提EKF快速算法检测性能的比较图。

图3是当谐波频率固定为0.06Hz时，不同信干噪比下主瓣和最大旁瓣的比值。比值大于零，则说明谐波信号容易被正确检测，反之，则不容易被正确检测。由仿真结果可知，本发明性能优于神经网络算法性能；在输入SINR小于-40dB时，本发明和基于SOCP最优滤波器算法性能相当，在输入SINR大于-40dB时，本发明性能优于基于SOCP最优滤波器算法性能。但本发明计算复杂度远低于基于SOCP最优滤波算法。因此，本发明有更强的实际工程意义。