末制导段的标控脱靶量解析制导方法与流程

本发明提供一种末制导段的标控脱靶量解析制导方法，尤其是指一种末制导段对地打击的标控脱靶量的制导方法，属于航天技术、武器技术领域。

背景技术：

零控脱靶量是寻的导弹末制导问题的一个重要概念，狭义的零控脱靶量指的是在导弹和目标均不进行机动的条件下，两者之间可达到的最小距离；广义的零控脱靶量则还包含终端角度误差、终端速度误差等。许多经典的制导方法，都是由零控脱靶量推导而来的，如比例导引律、增广比例导引律、弹道成型导引律等。这些导引律都是在简化的线性模型下推导而来，不需要计算零控脱靶量的具体值，控制指令可以直接表达为当前飞行状态的函数。但是真实的制导问题是非线性，上述经典导引律的不能完全满足现在的制导方法设计的需求。

标控脱靶量是在零控脱靶量的基础上发展出来的一个制导相关概念，指的是飞行器按照给定的标准控制指令飞行所得轨迹的终端状态与约束之间的偏差，用于解决非线性系统的制导问题。由于广义标控脱靶量通常需要通过求解非线性微分方程获得，目前多采用数值积分的方法进行求解。在获得广义标控脱靶量之后，既可以通过构造相关的负反馈对当前的标准控制指令进行修正，又可以采用优化算法对标准控制指令进行更新。如静态模型预测导引律、线性伪谱模型预测导引律等，也都是由标控脱靶量发展而来的制导律。

技术实现要素：

本发明的目的是提供一种寻的导弹末制导段标控脱靶量解析制导方法。该方法以零攻角为末制导段的标准控制；并采用正则摄动方法进行解析求解，从而获得了解析的标控脱靶量；最后构造相关的负反馈求解了修正标控脱靶量的制导指令，从而获得了一种寻的导弹末制导段非线性解析制导方法。

本发明为一种末制导段标控脱靶量解析制导方法，包括以下几个步骤：

步骤1：末制导段建模。地面看作曲率为零不旋转的惯性平面，在纵向平面内，航迹坐标系下的末制导导弹的运动方程如下所示：

上式中，y、h、v、γ和m分别为导弹射程、高度、速度、弹道倾角和质量；和分别为导弹的射程、高度、速度和弹道倾角对时间的导数；L、D分别为导弹的升力和阻力，与导弹的攻角、动压、气动系数等相关，其中攻角是控制量；g为重力加速度，与导弹高度相关；

末制导段通常采用零攻角作为标准控制，此时有L＝0，则可得标控弹道的运动模型为：

上式中，下标‘b’表征标控弹道，y_b、h_b、v_b、γ_b、m_b、D_b和g_b分别为标控弹道的射程、高度、速度、弹道倾角、质量、大气阻力和重力加速度。

步骤2：把末制导的标控弹道按正则摄动理论分为零阶标控弹道和一阶标控弹道。分别如下：注:为了便于表达，下文中标控弹道状态量下标“b”省去

上式中，上标和分别表征各状态量的正则摄动展开的零阶项和一阶项，以及零阶项和一阶项所决定的量。分别为末制导段标控弹道的射程、高度、速度和弹道倾角的零阶项；分别为末制导标控弹道的射程、高度、速度和弹道倾角的一阶项；和分别是取决于高度、速度的零阶项的重力加速度和大气阻力；D₀和v₀分别是初始大气阻力和初始速度。g_s是海平面的重力加速度；k是一个常值小量，k＝ε，ε是正则摄动展开的分阶符号。

步骤3：对末制导段标控弹道零阶项解析求解。对步骤2得到的标控弹道正则摄动零阶微分方程解析积分，可得标控弹道的射程、高度、速度、弹道倾角的解析解分别如下：

上式中，y₀、h₀、和x_γ0分别为末制导段的标控弹道的初始射程、初始高度、初始速度相关变量和初始弹道倾角相关的常数；a₀、a₁、a₂、b₀、b₁、b₂均为与初始弹道倾角相关的常数；k_v1、k_v2、为与初始速度、初始大气阻力相关的常数；k_y1、k_y2、k_y3、k_y4和k_y5为a₀、a₁、a₂、k_v1、k_v2的多项式。

步骤4：对末制导段标控弹道一阶项解析求解。利用步骤3中得到末制导段标控弹道零阶项的解析解，对一阶摄动微分方程中的系数进行多项式拟合，最后进行积分可得射程、高度、速度、弹道倾角一阶项的解析解分别如下：

上式中，k_1y2～k_1y13、k_1h2～k_1h13、k_1v1～k_1v9和k_1γ1～k_1γ5均为一阶微分方程中的拟合系数的多项式。

步骤5：获取标控弹道的完整解析解，计算制导指令。将步骤3和步骤4获得的末制导段标控弹道的零阶和一阶解析解带入下式，获得一阶精度的解析解。

标控脱靶量可以表示为

NEM＝(y_cf-y_f)sin(-γ_f)

上式中，y_cf为目标的位置，y_f和γ_f为标控弹道的射程和弹道倾角的终值。此时的法向控制指令可以表示为

上式中，a_n为导弹的法向加速度，为制导指令；N为导引系数，一般取3～5；t_go为末制导段的剩余飞行时间。

本发明的优点在于：

(1)提出了以零攻角作为寻的导弹末制导段的标准控制，不但简化了标控弹道的运动方程，而且使得制导修正所需的攻角位于零附近，降低了制导修正带来的速度损失。

(2)采用正则摄动方法解析求解了末制导段纵向弹道，获得了射程、高度、速度和弹道倾角高精度解析解。

(3)给出了一种基于广义标控脱靶量的制导方法，大大减小了导弹的法向加速度，同时使得终端攻角收敛到零。

附图说明

图1是标控弹道速度微分方程分解示意图；

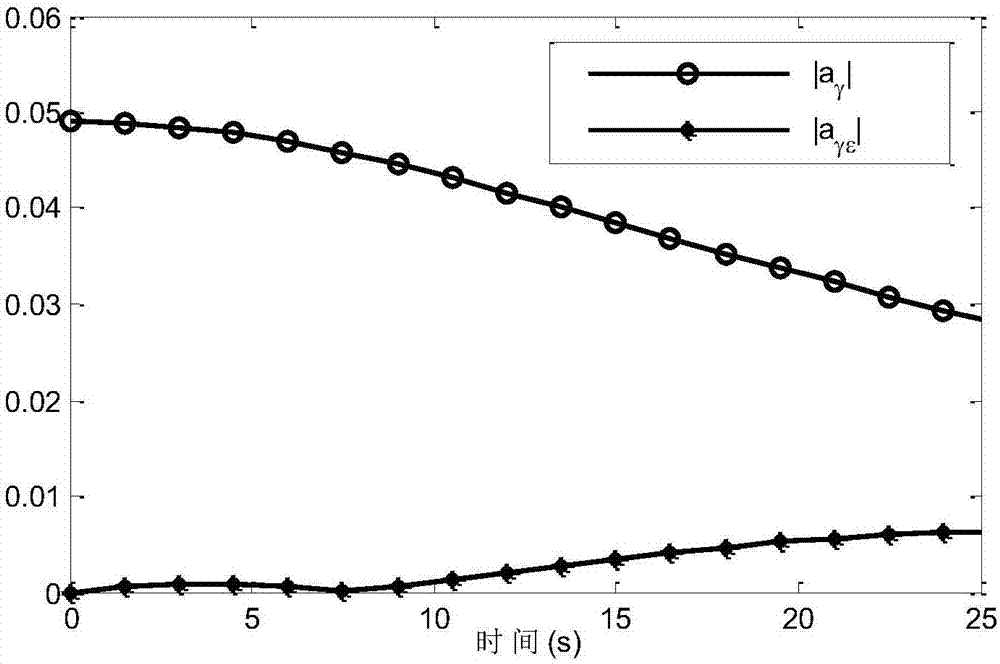
图2是标控弹道倾角微分方程分解示意图；

图3是标控弹道参数拟合示意图；

图4是标控弹道参数拟合示意图；

图5是标控弹道一阶微分方程参数分析；

图6是标控弹道一阶微分方程参数拟合示意图；

图7是标控弹道的射程解析解对比；

图8是标控弹道的高度解析解对比；

图9是标控弹道的速度解析解对比；

图10是标控弹道的弹道倾角解析解对比；

图11是标控弹道的解析解的绝对误差；

图12是碰撞前弹目几何关系示意图；

图13是本发明制导方法流程图；

图14是本发明制导方法示意图；

图15是本发明制导方法与比例导引律的弹道轨迹对比；

图16是本发明制导方法与比例导引律的弹道速度对比；

图17是本发明制导方法与比例导引律的弹道倾角对比；

图18是本发明制导方法与比例导引律的过载指令对比

具体实施方式

下面将结合附图和实施案例对本发明作进一步的详细说明。

针对寻的导弹末制导问题，本发明以零攻角作为寻的导弹末制导修正段的标准控制，并对标控弹道运动方程、制导修正一阶摄动方程进行过了建模；然后采用正则摄动方法对标控弹道进行解析求解，获得了导弹射程、高度、速度、弹道倾角的零阶项和一阶项的解析解；最后基于标控脱靶量构造负反馈形成的制导指令。

本发明是一种末制导段标控脱靶量解析制导方法，包括以下几个步骤：

步骤1：末制导段建模。地面看作曲率为零不旋转的惯性平面，在纵向平面内，航迹坐标系下的末制导导弹的运动方程如下所示：

上式中，y、h、v、γ和m分别为导弹射程、高度、速度、弹道倾角和质量；和分别为导弹的射程、高度、速度和弹道倾角对时间的导数；L、D分别为导弹的升力和阻力；g为重力加速度，与导弹高度相关。

上式中，C_L和C_D分别为升力系数和阻力系数，与攻角相关；S为弹道的气动参考面积；ρ为当地大气密度，通常采用指数大气模型：

ρ＝1.2251e^-h/7254.2kg/m³

末制导时控制指令为导弹的法向加速度，由升力决定，表达式如下：

a_n＝L/m

末制导段采用零攻角作为标准控制，此时有a_n＝0，L＝0，则可得标控弹道的运动模型为：

上式中，下标‘b’表征标控弹道，y_b、h_b、v_b、γ_b、m_b、D_b和g_b分别为标控弹道的射程、高度、速度、弹道倾角、质量、大气阻力和重力加速度。

步骤2：把末制导的标控弹道按正则摄动理论分为零阶标控弹道和一阶标控弹道。注:为了便于表达，下文中标控弹道状态量下标“b”省去。

把标控弹道的速度微分方程等号右边分为两部分，如下所示：

上式中，ε为正则摄动展开式分阶的标志，是一个常值小量，ε＝k，下同。a_v为初始的气动阻力加速度和海平面重力加速度在速度方向的分量，a_vε为由于位置和速度变化导致的气动阻力和海平面加速度在速度方向上分量的产生的偏差，一般情况下，a_v的绝对值远大于a_vε的绝对值，如图1。表达式如下：

同样标控弹道的弹道倾角微分方程等号右边也分为两部分，如下所示：

上式中，a_γ为海平面的重力加速度在初始速度下的等效弹道倾角变化率，a_γε为由于位置和速度变化变化，重力加速度加速度等效弹道倾角变化率的偏差。一般情况下，a_γ的绝对值远大于a_γε的绝对值，如图2。表达式如下：

根据正则摄动理论，可将y、h、v和γ展开为：

上式中分别表示对应变量的0阶、1阶，在后文中也表示0阶、1阶分量所决定的其他量，o(ε)表示忽略的高阶无穷小的分量。

零阶和一阶分量的初值分别取：

把式(6)带入式(1)，忽略高阶无穷小的项，整理可得

上式中，气动阻力重力加速度海平面重力加速度g_s、初始气动阻力D₀是常数。

将式(7)等号右边对ε进行一阶泰勒展开，根据等号左右两边ε等次幂的系数相等，可得标控弹道射程的零阶和一阶微分方程，如下：

同理可得标控导弹高度、速度、弹道倾角的零阶和一阶微分方程，分别如下：

上式中，表示零阶高度分量对应的重力加速度，表示零阶速度分量、零阶高度分量决定的气动阻力。

步骤3：对标控弹道零阶项解析求解。对步骤2得到的标控弹道正则摄动零阶微分方程解析积分，可得标控弹道的射程、高度、速度、弹道倾角的解析解。

为了便于求解，取

则

把式(17)带入式(20)可得

dx_γ/dt＝-2g_s/v₀ (21)

取对式(21)进行积分可得

上式中，x_γ0为x_γ初值，x_γ0＝ln[(1+sinγ₀)/(1-sinγ₀)]。

由式(22)和式(19)可得弹道倾角零阶分量的解析表达式为

把式(23)带入式(15)得

式(28)积分可得速度零阶解析式

上式中，

把式(23)和式(25)带入式(15)得

上式中，

对dh₁积分可得

dh₂、dh₃可以表示为时间的二次函数：

dh₂＝a₂t²+a₁t+a₀ (28)

dh₃＝b₂t²+b₁t+b₀ (29)

式中a₂,a₁,a₀,b₂,b₁,b₀为拟合系数，可以通过求解线性方程组获得。图3和图4分别为dh₂、dh₃的二次拟合效果，可见二次拟合可以达到很高的精度。

对dh₂、dh₃进行积分可得

由式(27)、(30)、(31)可得高度零阶解析式为

由式(23)可得可拟合为三次函数，如下

上式中，c₀,c₁,c₂,c₃为拟合系数。

把式(25)、式(33)带入式(11)得

式(34)积分可得

上式中，

k_y6＝a₂c₃/6

上式中，y₀、h₀、和x_γ0分别为末制导段的标控弹道的初始射程、初始高度、初始速度相关变量和初始弹道倾角相关的常数；a₀、a₁、a₂、b₀、b₁、b₂均为与初始弹道倾角相关的常数；k_v1、k_v2、为与初始速度、初始大气阻力相关的常数；k_y1、k_y2、k_y3、k_y4和k_y5为a₀、a₁、a₂、k_v1、k_v2的多项式。

步骤4：对末制导段标控弹道一阶项解析求解。利用步骤3中得到末制导段标控弹道零阶项的解析解，可以得到标控弹道一阶微分方程的系数矩阵。

由式(12、14、16、18)组成的标控弹道的一阶微分方程是一个线性时变系统，可以写为

上式中，

系数k_ij都是标控弹道变量的零阶分量函数，零阶分量在前面步骤中已经求出了解析表达式。为了便于求解一阶分量，需要对系数k_ij进行简化。用三次多项式拟合部分系数，如下：

结合式(25)、(28)、(33)和(37)可得其余系数的表达式：

图5给出了各个系数的原始数据和拟合结果的对比图，由图可看出拟合效果bi较好。(注：由于k₄₀在下文按小量处理，故不需要对其进行拟合处理。)图6给出了k₄₄、k₄₀的曲线，由图可知，k₄₄绝对值相对较小，接近于0，可看作一个小量。定义一个新变量小量则一阶的弹道倾角微分方程可以改写为

根据正则摄动理论，取代入式(39)可得

由式(40)展开可得变量z的零阶和一阶分量的微分方程，如下：

式(41)和式(42)积分可得

结合式(36-38)和(43)，对标控弹道的射程、高度、速度进行积分可得：

上式中，k_1y2～k_1y13、k_1h2～k_1h13、k_1v1～k_1v9积分得到的时间t多项式的系数，它们是关于a_i,b_i,c_i,d_i,e_i,p_i,的多项式。

步骤5：获取标控弹道的完整解析解，计算制导指令。将步骤3和步骤4获得的末制导段标控弹道的零阶和一阶解析解带入下式，获得一阶精度的解析解。

为了校验上述标控弹道解析解的精度，设末制导中导弹的初始高度为4000m，初始弹道倾角为0deg，初始速度为180m/s，分别采用数值积分和解析解的方法对标控弹道进行求解，得到的结果如图7-图10所示。由图可以看出，仅采用正则摄动零阶解时，高度、速度和弹道倾角的解析解存在着较大的误差；在考虑正则摄动一阶修正项的影响后，射程、高度、速度和弹道倾角的解析解均具有非常高的精度。图11进一步给出了解析解的误差分析。由图可以看出，末制导段碰撞前25s内，速度解析解的绝对误差小于1.2m/s；弹道倾角解析解的绝对误差小于0.4deg；射程解析解的绝对误差小于1m；高度解析解的绝对误差小于25m，高度误差相对较大，但是由图可知，随着剩余飞行时间减少，误差最终收敛至0，对制导不会产生大的影响。

本文中考虑打击地面固定目标的末制导情况，末端弹目几何关系如图12。基于标准控制的脱靶量(NEM)可以表示为

NEM＝(y_cf-y_f)sin(-γ_f) (47)

y_cf表示制导任务确定的目标位置，y_f为标控弹道预测的终点位置。

制导需要的剩余飞行时间t_go,可以近似用导弹撞击地面的时间来替代。导弹高度的解析式已经得到，只需要用Newton法2-3次迭代即可获得满足精度要求的t_go:

基于标控脱靶量的导引指令可以表示为

上式中，a_n为导弹的法向加速度，为制导指令；N为导引系数，一般取3～5；t_go为末制导段的剩余飞行时间。

制导流程如图13。制导过程说明如下：

步骤(1)初始化。设置导弹、目标初始信息。

步骤(2)解析预测标控脱靶量NEM并计算剩余飞行时间t_go。

步骤(3)判断标控脱靶量是否满足精度要求。如果满足，则当前法向过载指令为0，执行(5)；如果不满足，当前法向过载指令为执行(4)；

步骤(4)控制限幅。判断法向过载指令是否超过最大法向过载，如果超过，则按最大法向过载执行

步骤(5)导弹在当前法向过载指令下继续飞行，并把更新的状态作为初始状态，以便用于预测NEM。

步骤(6)判定是否命中目标。如果是，则结束；否则，继续执行(2)；

整个制导的过程是从步骤(1)-步骤(6)循环的过程。如图14，在这个过程中，标控弹道也不断更新直至标控弹道命中目标，弹道的实际弹道也在法向过载指令的作用下，不断的向标控弹道收敛，最后和命中目标的标控弹道重合，法向过载指令也收敛到0。

实施案例

为了验证本导引律的优势，进行仿真实验，并与比例导引律进行对比。导弹初始条件为y₀＝0，h₀＝4000m，v₀＝180m/s，γ＝20°，地面固定目标的位置y_cf＝5000m。仿真时考虑一阶延迟环节:

a_L＝(a_n-a_L)/t_T (50)

上式中，a_n是指令法向加速度，a_L为实际法向加速度，时间常数为t_τ＝0.3s。

图15-图18给出了标控脱靶量导引律和比例导引律弹道、速度、弹道倾角、法向过载的对比。前者飞行时间是35.25s，后者为42.03s，通过图15可以看出，前者弹道更短更直接。两者脱靶量都很小，前者脱靶量为0.007m，后者脱靶量为0.002m，都能满足命中目标的要求。由图16可知，在同一时间点，前者速度一直保持大于后者的速度。前者终端速度为269.44m/s大于后者的终端速度为261.66m/s。由图18可知，前者对法向指令过载远小于后者法向指令过载，且前者法向指令过载最后收敛到0，即可以保证末端攻角为0。下表1为标控脱靶量和比例导引律对比。

表1。