对多普勒信息不敏感的低旁瓣波形设计方法与流程

本发明属于波形设计技术领域，具体涉及一种对多普勒信息不敏感的低旁瓣波形设计方法。

背景技术：

雷达的工作原理是：发射电磁波对探测区域进行照射并接收回波，通过对比发射信号与回波信号的频率、时延等推测计算探测目标的距离、位置、高度、角度、速度等信息。如图1所示的雷达探测工作原理的示意图。因此，探测波形对于雷达探测性能至关重要。自相关函数旁瓣越低的探测信号，雷达探测的精度越高。

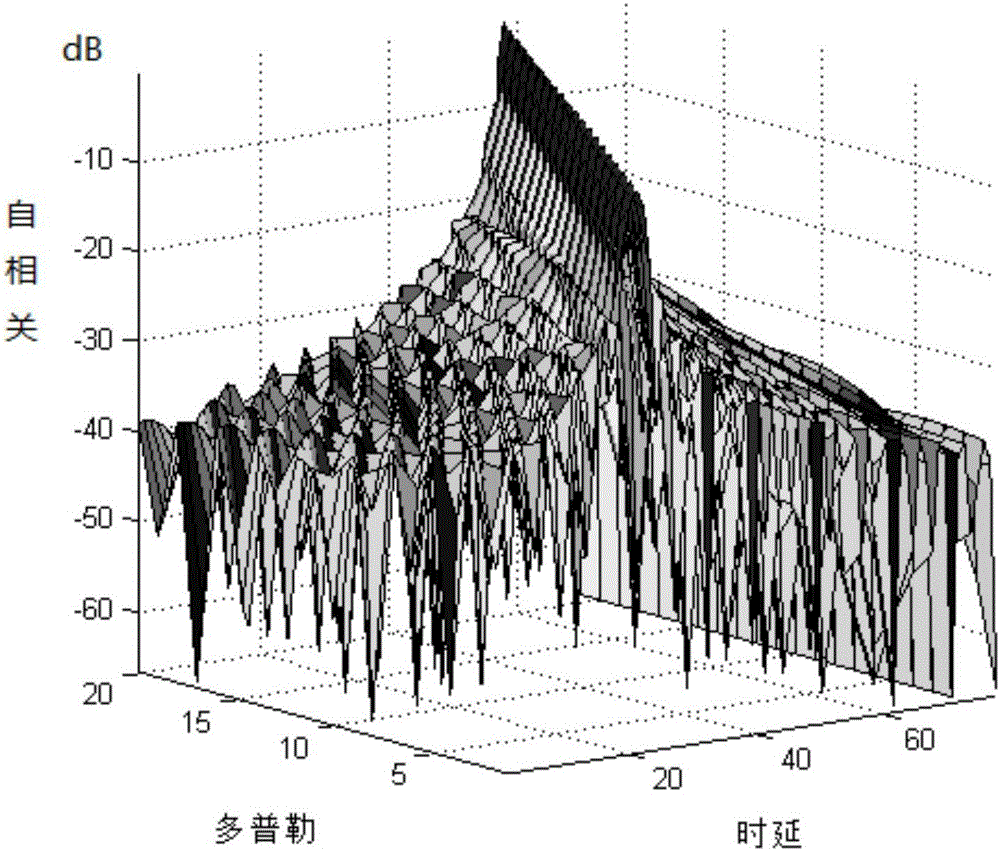
目前，对运动目标的检测普遍采用的是线性或非线性调频信号。线性或非线性调频信号的设计简单。线性调频信号的“时延-多普勒”自相关见图2。图2中可见，其时延因子与多普勒因子在特定范围内的旁瓣会出现尖峰；线性或非线性调频信号的起始频率、终止频率与调频函数一旦被对方确认后，发射信号对于对方将无任何秘密而言。

考虑到实际应用中，只需要探测感兴趣区域的目标信息，对此，Hao He及国际雷达信号处理专家Jian Li教授、PetreStoica教授的著作《Waveform Design for Active Sensing Systems-A computational approach》(Cambridge University Press，July，2011，pp.88-106)对感兴趣的“时延-多普勒”区域提出了低自相关旁瓣设计方法(本发明称其为He-Li-Stoica方法)。He-Li-Stoica方法可以看做是在“时延-多普勒”区域上开了个窗，使得探测波形在该窗口内的整体旁瓣电平(Integrated Sidelobe Level，ISL)取得极小值。仿真结果见图3。该方法在窗口内的整体旁瓣电平较低，但个别“时延-多普勒”上(尤其是窗口边缘)的自相关旁瓣较大。在实际探测工作中，目标可能出现在该窗口内的任意“时延-多普勒”上，因此，较大的个别“时延-多普勒”上的自相关旁瓣影响实际探测的性能。

因此，上述波形设计方法都存在一定的局限性和不可靠性。

技术实现要素：

本发明的目的是提供一种对多普勒信息不敏感的低旁瓣波形设计方法，解决了现有的目标检测波形设计方法存在的个别“时延-多普勒”上的自相关旁瓣较大的问题。

本发明所采用的技术方案是，对多普勒信息不敏感的低旁瓣波形设计方法，具体按照以下步骤实施：

步骤1：构建“时延-多普勒”范围内低自相关旁瓣波形设计的复数数学模型，对该数学模型的系数矩阵进行分割得到矩阵的实系数矩阵与虚系数矩阵并将非正定的实系数矩阵与虚系数矩阵转换为正定矩阵；

步骤2：使用ADMM方法对目标函数进行变换求解引入变量；

步骤3：用分段最小值法求解不等式约束问题；

步骤4：使用MM方法得到满足约束条件的探测波形x；

步骤5：重复步骤3、4直至x收敛。

本发明的有益效果是：本发明对多普勒信息不敏感的低旁瓣波形设计方法，所设计的波形在一定“时延-多普勒”区域内的每个自相关旁瓣很小，均小于-40dB，满足特定距离和速度范围内运动目标的高分辨率探测需求，同时，本发明方法设计的波形具有多样性，因此还具备反侦察特性。

附图说明

图1是雷达探测工作原理示意图；

图2是线性调频信号的自相关三维图；

图3是He-Li-Stoica方法设计的波形的自相关三维图；

图4是本发明方法的自相关旁瓣迭代结果图；

图5是本发明方法设计的波形的自相关三维图。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明。

本发明对多普勒信息不敏感的低旁瓣波形设计方法，首先，构建“时延-多普勒”范围内低自相关旁瓣波形设计的复数数学模型，该复数模型的目标函数是一元一次函数，约束条件中包含有多元四次方不等式，对该数学模型的系数矩阵进行分割得到矩阵的实系数矩阵与虚系数矩阵并将非正定的实系数矩阵与虚系数矩阵转换为正定矩阵；其次，使用ADMM框架将上述模型分解为若干模型，并分别用分段最小值法与MM方法解决不等式约束与多元四次方优化问题，解出自相关旁瓣约束变量ε、替代变量F_lk、G_lk与信号变量从而得到满足约束条件的探测波形x。

本发明对多普勒信息不敏感的低旁瓣波形设计方法，就是设计一个长度为N的模为1的信号序列x＝{x₁,...,x_N}，使得信号序列在指定范围内多普勒与时延的自相关r的模满足|r|≤ε。

具体实施过程为：

步骤1：数据与模型预处理

将“时延-多普勒”范围内的自相关函数的实部与虚部进行分离。根据给定的时延范围与多普勒范围，计算范围内的不同时延与多普勒对应的实部系数矩阵与虚部系数矩阵的正交分解向量。此时，自相关由实部系数矩阵与虚部系数矩阵表示。对得到的各正交分解向量进行实部与虚部的分离，构成新的系数矩阵。

仅考虑时延K_k∈{K_d,...,K_u}(k＝1,...,K,0<K_d<K_u<N)时，非周期自相关函数

同时考虑时延K_k与多普勒L_l∈{L_d,...,L_u}(l＝1,...,L,L_d<L_u)因素时，非周期自相关函数写为：

r_lk＝x^HA_lkx (1)

其中，

x为长度为N的模为1的信号序列，x＝[x₁,...,x_N]^T,lk＝1,...,LK,LK＝L×K

算子diag(·)是将向量扩展为对角矩阵，使得D_l(n,n)＝d_l(n)。

那么，满足要求的波形设计的数学描述为：

对系数矩阵A_lk进行分割得到：

其中，

显然，RE_lk与IM_lk满足：

1)

2)x^HRE_lkx与x^HIM_lkx均为实数。

那么，自相关函数r_lk与RE_lk、IM_lk满足关系：

4|r_lk|²＝(x^HRE_lkx)²+(x^HIM_lkx)² (4)

为了后续使用MM方法，需要将非正定的实系数矩阵与虚系数矩阵转换为正定矩阵，即系数矩阵的特征值均大于零。详细过程见式(5)与式(6)。

对系数矩阵RE_lk进行特征分解，得到特征根{λ₁,...,λ_N},记MR_lk＝min{λ₁,...,λ_N},其中min{·}表示求·中的最小元素。

若MR_lk≤0,则：

MR_lk＝MR_lk-0.1

若MR_lk>0,则：

其中E_N为N阶单位矩阵，即：

显然，是正定矩阵。正定矩阵均可分解为一对对称矩阵的乘积，因此正定矩阵分解为：

其中，

同理，系数矩阵IM_lk对应的正定矩阵分解为：

其中，

系数矩阵IM_lk的特征根的最小值,记为MI_lk。

那么式(1)可以表示为：

根据信号序列x的模为1即x^Hx＝1可得

式(8)可以写成另外一种实数形式：

其中，Re(·)与Im(·)分别表示·的实部与虚部。

则是实对称矩阵，即：

证明：由式(6.1)有

则Re(W_lk)^T＝Re(W_lk),Im(W_lk)^T＝-Im(W_lk)

同理可证

由式(9)，式(4)可以表示为：

令替代变量F_lk与G_lk分别为则式(10)可以表示为：

则式(2)表示为：

步骤2：基于步骤1得到的系数矩阵，使用ADMM方法对目标函数进行变换求解引入变量，即使用ADMM方法来求解规划式(12)。

引入拉格朗日乘子α_lk,β_lk与ADMM乘子ρ>0，式(12)可表示为

步骤3：使用分段最小值法求解不等式约束问题，从而更新ε(t+1),F_lk(t+1),G_lk(t+1),α_lk(t+1),β_lk(t+1)

①更新F_lk(t+1),G_lk(t+1)

约束与变量无关，它们仅在迭代求解F_lk,G_lk的时候起作用，而约束与变量F_lk与G_lk无关，它们仅在迭代求解的时候起作用。所以对于给定t次的求解ε(t+1),F_lk(t+1),G_lk(t+1)的问题，式(13)可表示为：

记

那么式(14)可以简化为：

由式(14)的约束条件可知，变量F_lk,G_lk的取值是受变量ε约束的。而对于给定的ε，式(14)的F_lk(t+1),G_lk(t+1)为：

其中，

显然，记为S_lk，则：

②更新ε(t+1)

给定t次的求解ε(t+1)。将式(17)、(18)代入式(16)得：

忽略掉常数项，式(19)简化为：

其中，

显然，因为式(18)的分段情况，一般情况下式(20)是不连续的，需要分段讨论其极小值点。分段讨论式(20)时，分段的分割点取值范围为其中，ε_max是代入原问题得到的ε，ε₀是大于0且小于ε_max与的实数。

在区间[ε_d,ε_u]上，ρ>0且S_lk≥0，所以A,B>0，故式(20)取极小值时的ε为：

将式(21)代入式(20)得到L在各段的极小值{L₁,...,L_m}，选取{L₁,...,L_m}中最小值对应的ε为ε(t+1)。

③更新拉格朗日乘子α_lk(t+1),β_lk(t+1)

步骤4：推导目标函数及目标函数的最优函数，从而将四次型目标函数降幂为一次型函数，然后在一次型最优函数的基础上，使用MM方法求解满足约束条件的信号序列。即已知α_lk(t+1)，ε(t+1)，β_lk(t+1)，F_lk(t+1)，G_lk(t+1)，求解

步骤4.1：推导目标函数

同理于式(14)，求解时，式(13)可写为：

将式(23)中的常数项去掉后，得到关于的目标函数：

步骤4.2：求解目标函数(24)的优化函数

显然，目标函数(24)为的四次方函数，为了求解找到式(24)的优化函数，使得该优化函数是的一次函数，再使用MM方法求解

式(24)右端第一项有：

其中，因为是实对称矩阵，故而是实对称矩阵，矩阵

也是对称矩阵。

因为，二次型函数f(x)＝x^HAx，若A,B是n×n的自共轭矩阵且A≤B，那么

根据式(27)

其中，是的最大特征根，

因为所以式(28)的第二项是常数将式(28)的常数项用C_W1表示，即：

则式(28)可写为：

又

其中，

与均为实对称矩阵，故M₁是实对称矩阵。

那么根据式(27)，若是M₁的最大特征根，则：

令

则

同理，式(24)右端第二项

其中，是M₁的最大特征根，是的最大特征根。

式(24)右端第三项的优化函数的推导过程类似于式(31)，优化函数为：

其中，

所以，式(24)的优化函数为：

步骤4.3：更新

式(36)的拉格朗日函数为：

对拉格朗日函数(37)关于求偏导

因为是关于的一次函数，所以其对的偏导是常数，记为d_n，令则：

将式(39)代入约束条件得

将式(40)代入式(36)目标函数可知，μ_n取值为因此

将式(41)计算得到的代入

中，得到本轮迭代的x。

步骤5：重复步骤3-4，直至x收敛。

实施例

为了证明本发明方法的有效性，把He-Li-Stoica方法产生的波形、线性调频信号波形与本发明方法产生的波形做比较，下面结合具体实例以及图表进行详细说明。

我们仿真设计长度为N＝128的波形，要求其在“时延-多普勒”区域[L_min,L_max]×[K_min,K_max]为[-2,2]×[-8,8]内的探测波形的自相关旁瓣低于-40dB，ρ＝0.1。

步骤1：构建模型基本框架并初始化数据。根据[L_min,L_max]×[K_min,K_max]的值设定LK＝(L_max-L_min)×(K_max-K_min)，那么非周期的“时延-多普勒”的低自相关旁瓣的探测波形x＝{x₁,...,x_N}的设计问题定义为：

其中x＝[x₁ ... x_N]^T,A_lk是已知的矩阵，其具体形式为

随机初始化x(0)，得

根据式(2)得到初始自相关函数的模|r_lk(0)|以及初始ε(0)＝max{|r_lk(0)|,lk＝1,...,LK}。其中，MR_lk,MI_lk,的计算步骤如下：

对系数矩阵A_lk进行分割得到为了后续使用MM方法，需要将非正定的实系数矩阵与虚系数矩阵转换为正定矩阵，即系数矩阵的特征值均大于零。对矩阵RE_lk进行特征分解，得到特征根{λ₁,...,λ_N},记MR_lk＝min{λ₁,...,λ_N},其中min{·}表示求·中的最小元素。若MR_lk≤0,则MR_lk＝MR_lk-0.1,若MR_lk>0,则MR_lk＝0,其中N阶单位矩阵分解为其中同理，系数矩阵IM_lk对应的正定矩阵分解为其中系数矩阵IM_lk的特征根的最小值,记为MI_lk。

步骤2：构建低自相关旁瓣的“时延-多普勒”波形设计问题的ADMM框架，并初始化ADMM相应的参数。

引入拉格朗日乘子α_lk,β_lk、替代变量与ADMM乘子ρ>0，波形设计问题(1)可表示为

其中，

初始化F_lk(0),G_lk(0)：

随机初始化α_lk(0),β_lk(0)。

步骤3、使用分段最小值法求解不等式约束问题，进而更新ε(t+1),F_lk(t+1),G_lk(t+1),α_lk(t+1),β_lk(t+1),lk＝1,...,LK

对于给定的ε(t)，更新替代变量F_lk(t+1),G_lk(t+1)为

其中

给定t次迭代的求解ε(t+1)，具体步骤如下。

在ε的取值区间[ε_d,ε_u]上

其中

因为ρ>0且S_lk≥0，所以A,B>0，故取极小值时的ε为

根据上述步骤，计算L_ε在ε的所有可能取值区间[ε_d,ε_u]上的极小值{L₁,...,L_m}，选取{L₁,...,L_m}中最小值对应的ε为ε(t+1)。

更新拉格朗日乘子α_lk(t+1),β_lk(t+1),lk＝1,...,LK为

步骤4、使用MM方法求解四次方优化问题。已知ε(t+1)，α_lk(t+1)，β_lk(t+1)，F_lk(t+1)，G_lk(t+1)，lk＝1,...,LK，更新为

其中，d_n是拉格朗日函数

对的偏导。

上述拉格朗日函数中，

和分别是M₁和M₂的最大特征根，和是和的最大特征根。

步骤5、重复步骤3至步骤4，直至x收敛。

图4是本发明方法的自相关旁瓣迭代结果图。设计得到的波形的“时延-多普勒”[L_min,L_max]×[K_min,K_max]为[-2,2]×[-8,8]的自相关旁瓣三维图见图5。