一种智能果园路径规划方法与流程

本发明涉及路径规划技术领域，尤其涉及一种智能果园路径规划方法。

背景技术：

随着中国经济的不断发展，城市日新月异，科技化自动化水平不断提高，但是相比之下，农村的现代化水平有待改善。尽管“村村通”这一系统工程的开展使农村的交通情况得到了很大的改善，尤其对于果农而言，果农不再为农产品如何运输烦恼，但是在规模比较大的果园内农药喷洒路径的确定以及农产品采摘路径等的确定依然是一个重要的研究问题,就农药喷洒而言，选择合适的喷洒路径，不仅节省了人力油费，还减少了农药的浪费。本文就是在此研究背景的基础上，对果园内农药喷洒或者农作物采摘等最优路径的选择进行研究分析。

技术实现要素：

针对现有技术的不足，本发明提供了一种智能果园路径规划方法。

本发明所采取的技术方案是一种智能果园路径规划方法：包括以下步骤：

步骤1：对果园内的实际分布格局进行简化，建立果园简化模型；

步骤2：对简化模型进行参数设置，包括果树位置，小车位置的初始化设置，果树距离、小车距果树的距离设置，以及小车必经路径的节点设置；

步骤3：分别利用dijkstra算法和floyd算法研究了简化模型的小车行驶路径，计算了小车遍历完所有节点的路径的数值；

所述的dijkstra算法是从一个顶点到其余各顶点的最短路径，即单源最短路径算法，使用广度优先搜索策略，以起始点为中心向外层层扩展，直到扩展到终点为止，根据步骤1建立的果园简化模型建立邻接矩阵x＝[a][b]，矩阵对应点为两节点之间的最短距离，两节点重合记为0，不接触记为无穷大，对距离最短距离节点进行累加即可获得最短路径；

所述的floyd算法是一种利用动态规划思想寻找给定的加权图中多源点之间最短路径的算法，从任意一条单边路径开始，所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大；对于每一对顶点i和j，判断是否存在一个顶点k使得从i到k再到j比已知的路径更短，如果存在则对顶点进行更新，如果不存在这说明ij此时距离最短；

根据步骤1建立的果园简化模型建立邻接矩阵d＝[i][j]，如果从顶点i到顶点j有路可达，则d[i][j]＝d，d表示该路径的长度；否则d[i][j]＝∞；定义一个矩阵p用来记录该路径上所插入点的信息，p[i][j]表示从顶点i到顶点j需要经过的点，初始化p[i][j]＝j，把从顶点i到顶点j路径上各个插入点插入简化模型中，依次比较插点后的路径距离与原来的距离，设kg为插入点，g＝0,1，…n；从初始插入点k0开始，比较d[i][k0]+d[k0][j]与d[i][j]的值，若d[i][k0]+d[k0][j]<d[i][j]，则d[i][j]＝d[i][k0]+d[k0][j]，p[i][j]＝k0，k0表示找到的距离更短的点，在d中包含有两点之间最短道路的信息，而在p中则包含了最短通路径的信息，并继续比较d[i][kg]+d[kg][j]与d[i][j]的值，若d[i][kg]+d[kg][j]≥d[i][j]，则该插入点不是距离更短的点，继续比较下一组d[i][kg]+d[kg][j]与d[i][j]的值；

步骤4：确定适用该果园简化模型的最优路径。

采用上述技术方案所产生的有益效果在于：

本发明提供了一种智能果园路径规划方法，利用dijkstra算法和floyd算法以及matlab工具分析研究了简化模型的农药喷洒路径，确定了小车遍历完所有节点的最优路径及最优路径的数值，从而确定了适用该模型的果园果实采集或农药喷洒的最优路径。

附图说明

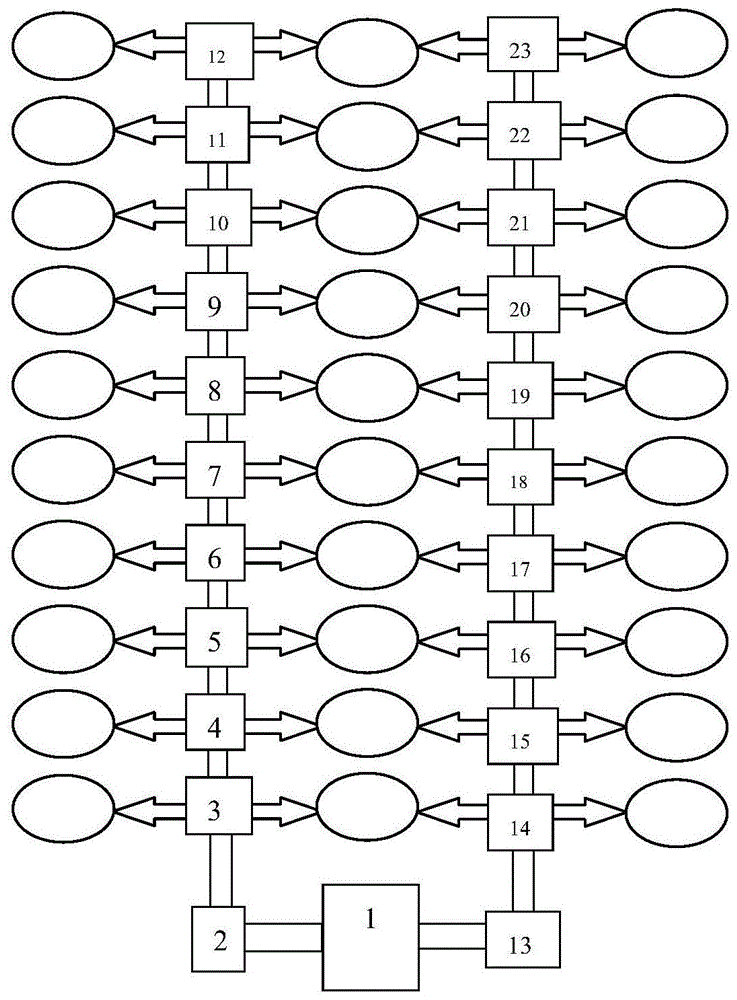
图1为本发明的果园简化模型示意图；

图2为本发明使用dijkstra算法建立的邻接矩阵示意图；

图3为本发明使用dijkstra算法计算的最优路径示意图；

图4为本发明使用floyd算法建立的邻接矩阵示意图

图5为本发明使用matlab运行结果截图；

图(a)-路径的邻接矩阵d，图(b)-路径所经过的端点顺序p；

图6为本发明使用floyd算法计算的最优路径示意图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

一种智能果园路径规划方法，包括以下步骤：

步骤1：对果园内的实际分布格局进行简化，建立果园简化模型；

本实施例中简化模型如图1所示，椭圆代表果树，共计三列30个，方框1表示起点位置，也就是小车的起点位置，三列果树中间为两条过道，方框3-12,14-23为节点位置，即两棵果树之间的中间位置。需要解决的问题是转化为方框1遍历完所有椭圆路径总和的最优。由于小车在过道选择果树进行采摘或农药喷洒时，选择左边或者右边一颗果树采摘或喷洒结束后再去相反方向进行果树操作时路线是最优的，因此我们假设1,2距离为单位长度1的情况下，2到节点3的距离默认为5(默认小车到了节点3之后左右各喷洒了一次农药之后回到节点3)。

步骤2：对简化模型进行参数设置，包括果树位置，小车位置的初始化设置，果树距离、小车距果树的距离设置，以及小车必经路径的节点设置；

步骤3：分别利用dijkstra算法和floyd算法研究了简化模型的小车行驶路径，计算了小车遍历完所有节点的路径的数值；

所述的dijkstra算法是从一个顶点到其余各顶点的最短路径，即单源最短路径算法，使用广度优先搜索策略，以起始点为中心向外层层扩展，直到扩展到终点为止，dijkstra算法每次新扩展一个距离最短的点，更新与其相邻的点的距离。当所有边权都为正时，由于不会存在一个距离更短的没扩展过的点，所以这个点的距离永远不会再被改变，因而保证了算法的正确性。不过根据这个原理，用dijkstra求最短路的图不能有负权边，因为扩展到负权边的时候会产生更短的距离，有可能就破坏了已经更新的点距离不会改变的性质，适用于求解小型网络中指定两结点之间的最优路径，适合求解单源、无负权的最短路，其时效性较好，但当路网复杂，结点较多时，dijkstra算法虽能找到最优解,但其搜索速度较慢。

根据步骤1建立的果园简化模型建立邻接矩阵x＝[a][b]，矩阵对应点为两节点之间的最短距离，两节点重合记为0，不接触记为无穷大，对距离最短距离节点进行累加即可获得最短路径；

如图2所示为根据模型建立的邻接矩阵，对应框格为两节点之间的最短距离，两节点重合记为0，不接触记为无穷大，其中(1，1)为0，(1，2)为n,(1,3)为∞。标记单元格表示节点之间的最短路径，对标记单元格进行累加即可得到最短路径，如下述公式所示，小车行走路线如图3所示。

所述的floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法。在计算机科学中，floyd算法是一种在具有正或负边缘权重(但没有负周期)的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度(加权)。虽然它不返回路径本身的细节，但是可以通过对算法的简单修改来重建路径。从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大，对于每一对顶点i和j，判断是否存在一个顶点k使得从i到k再到j比已知的路径更短，如果存在则对顶点进行更新，如果不存在这说明ij此时距离最短；

根据步骤1建立的果园简化模型建立邻接矩阵d＝[i][j]，如果从顶点i到顶点j有路可达，则d[i][j]＝d，d表示该路径的长度；否则d[i][j]＝∞；定义一个矩阵p用来记录该路径上所插入点的信息，p[i][j]表示从顶点i到顶点j需要经过的点，初始化p[i][j]＝j，把从顶点i到顶点j路径上各个插入点插入简化模型中，依次比较插点后的路径距离与原来的距离，设kg为插入点，g＝0,1，…n；从初始插入点k0开始，比较d[i][k0]+d[k0][j]与d[i][j]的值，若d[i][k0]+d[k0][j]<d[i][j]，则d[i][j]＝d[i][k0]+d[k0][j]，p[i][j]＝k0，k0表示找到的距离更短的点，在d中包含有两点之间最短道路的信息，而在p中则包含了最短通路径的信息，并继续比较d[i][kg]+d[kg][j]与d[i][j]的值，若d[i][kg]+d[kg][j]≥d[i][j]，则该插入点不是距离更短的点，继续比较下一组d[i][kg]+d[kg][j]与d[i][j]的值；

本实施例中先对矩阵s进行初始化，之后分别以顶点1、顶点2…顶点23为中介点对矩阵s进行初始化，最终矩阵d如图4所示。图中所示的框格的所在行和列表示从一节点到另一节点的距离，如果行表示的数字小于列表示的数字，则记为inf。例如，第一行第三个框格表示1节点到3节点的距离6，使用matlab编写程序，得出运行结果，如图5所示，由图(b)可知，最优路径为1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21-22-23，根据路径的邻接矩阵对最优路径进行叠加得到最多路径113，行走路线如图6所示，

步骤4：确定适用该果园简化模型的最优路径。

以上实施例仅用以说明本发明的技术方案，而非对其限。尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解；其依然可以对前述实施例所记述方案进行修改，或对其中部分或全部技术特征进行等同替换；而这些修改或替换皆应在有专利要求书所确定的保护范围内。