一种基于正交匹配追踪算法的核磁共振T2谱反演方法与流程

本发明涉及信号处理、核磁共振测井T₂谱反演的技术领域，具体涉及一种基于正交匹配追踪算法的核磁共振T₂谱反演方法。

背景技术：

核磁共振(NMR)测井技术是测量岩层孔隙度以及流体饱和度的一种很有效的方法。在国内外石油、天然气勘探领域有着特别广泛的应用。而对NMR测井仪测到的自旋回波信号进行反演解释则是核磁测井理论的关键部分。

核磁共振测井得到的数据是自由感应衰减信号，通常要经过反演得到回波串的横向弛豫分量的T₂谱分布，然后利用得到的T₂谱分析出流体特性。因此T₂谱反演工作对于后续准确计算储集层信息非常重要。但是由于回波信号十分微弱，且存在非常强的噪声干扰，使得数据信噪比很低。所以在低信噪比条件下如何精确的反演出T₂谱是核磁测井领域中非常重要的研究课题。而提出一种在信噪比较低、T₂谱布点数较多的情况下能够较准确反演出T₂谱的方法很有必要。

文章【1】(尚卫忠.应用奇异值分解算法的核磁共振测井解谱方法[J].石油地球物理勘探,2003,38(1):91-94.)提出基于奇异值分解(SVD)算法的T₂谱反演算法，原理简单，易于实现，以一种简单的方式实现了出色的效果。虽然该算法很经典，但是也存在一些局限性。例如在信噪比较低的情况下反演精度较差、T₂谱布点数较多的情况下末端容易出现非零现象，因此缺乏实际的应用性。

文章【2】(林峰.基于奇异值分解法的核磁测井数据反演方法研究[D].吉林大学,2014.)中指出奇异值分解算法的求解精度与奇异值保留数有关，通过信号信噪比调节奇异值保留数可以很有效的提高T₂谱反演精度。因此提出基于奇异值分解法的线性截断算法。该算法可以快速有效地实现T₂谱反演，而且该算法比传统的奇异值分解算法更加稳定，即在信噪比变化很大情况下解的变化相对不大。线性截断算法可以适用于低信噪比(SNR>10)的T₂谱反演，在信噪比很低时(SNR>5)仍能较好地保持弛豫谱分布的真实性。但是在信噪比较低、T₂谱布点数较多的情况下很难避免末端非零现象。

文章【3】(Y.C.Pati,R.Rezaiifar,P.S.Krishnaprasad.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition[C].Proceedings of the Twenty-Seventh Asilomar Conference on Signals,Systems and Computers,1993,40～44.)中针对匹配追踪(MP)算法不易收敛的问题，提出了正交匹配追踪(OMP)算法。其在迭代的每一步都保持残差与解的正交性，以此来改善算法的收敛性。正交匹配追踪算法在稀疏问题的求解方面有着广泛的应用。这种方法通过迭代的方式确定解中的非零值，然后用稀疏值对信号进行稀疏表示。T₂谱反演问题并不是传统的稀疏问题，但是可以利用求解稀疏问题先确定非零值、然后在非零值范围内进行解谱工作的思想。这样既可以提高解谱精度又可以解决末端非零问题。因此需要针对T₂谱反演问题对正交匹配追踪算法进行修改，以使其适应T₂谱反演问题。

技术实现要素：

本发明目的在于：1)提高奇异值分解算法计算精度；2)利用正交匹配追踪算法解决T₂谱布点较多时出现的末端非零现象；3)在信噪比较低且T₂谱布点数较多的条件下得到较精确解。

本发明采用的技术方案为：一种基于正交匹配追踪算法的核磁共振T₂谱反演方法，该方法使用正交匹配追踪算法确定T₂谱非零值范围，然后再用正则化方法改进的奇异值分解算法在非零值范围内求取T₂谱，该方法具体包括如下步骤：

步骤1)、读取原始测井数据Y；

步骤2)、对数据进行中值滤波处理，并计算出信号矩阵A；

步骤3)、使用正交匹配追踪算法计算出T₂谱非零区域；

步骤4)、在T₂谱非零区域内用正则化方法改进的奇异值分解算法计算出问题的T₂谱；

步骤5)、计算误差是否在允许范围内；若在允许范围内则输出最终T₂谱，否则把计算出的T₂谱当做初始解返回步骤4)重新计算；

步骤6)、输出最终T₂谱。

进一步的，所述步骤3中使用正交匹配追踪算法计算T₂谱非零区域的过程为：

(1)初始化：残差r₀＝Y，Y为测量得到的信号，索引集V₀＝Φ，Φ为空集，权重ω₀＝[1,1,…，1]，ω₀为n维行向量，n为回波个数，迭代次数t＝l；

(2)从信号矩阵A中选出和残差最相关列：n_t为列序号，它代表第t次迭代的残差r_t-1与索引集V_t-1中的第i项v_i的点乘结果中最大值的序号；

(3)判断＜r_t-1,v_i>是否为负，若为负，则迭代结束，输出索引集V_t；

(4)将最相关列序号n_t所对应的列向量添加进下一次迭代索引集V_t中，更新索引集中已选列空间：

(5)利用改进的SVD算法求解线性方程组，并保证解的残差最小，获得的解x可以看作信号Y投影到索引集V_t上的最佳系数，将新得到的解作为V_t各列的稀疏系数值

(6)利用本次迭代权重w_t-1以及向量weight更新第t+1次迭代权重w_t：w_t＝w_t-1×weight，weight为值在0.5～2范围内线性排列的向量，其中距n_t位置最近的值为2，最远的值为0.5；

(7)更新带权重的残差：转到步骤(2)。

进一步的，所述奇异值分解算法线性截断过程为：

(1)对信号矩阵A_n×m做奇异值分解，即存在n×n维的正交矩阵U和m×m维的正交矩阵V，以及n×m维对角矩阵S，使得：A＝USV^T，其中m为弛豫分量数，n为回波个数；

(2)根据弛豫分量数m、回波个数n计算参数a，b：

$a=1+0.05m,b=35\ln m-58+\frac{0.16\×(n-125)}{\sqrt{m}}$

(3)根据线性截断SVD算法公式计算出解T₂谱X：

其中ω为信号矩阵A奇异值分解得到的对角矩阵S相应位置的元素值，Y为测量得到的信号；

进一步的，所述正则化方法计算过程为：

(1)计算根据弛豫分量数m、回波个数n计算参数a，b：

$a=1+0.05m,b=35\ln m-58+\frac{0.16\×(n-125)}{\sqrt{m}}$

(2)根据参数a,b以及信噪比SNR计算出正则化因子α：其中ω₁为信号矩阵A奇异值分解得到的对角矩阵S的第一个元素值；

(3)将测的信号Y、信号矩阵A以及单位矩阵I代入零阶正则化方法公式求解T₂谱X得：X＝(A^TA+αI)^-1A^TY。

进一步的，所述正则化方法改进的奇异值分解算法具体过程为：

(1)对信号矩阵A_n×m做奇异值分解，即存在n×n维的正交矩阵U和m×m维的正交矩阵V，以及n×m维对角矩阵S，使得：A＝USV^T，其中m为弛豫分量数，n为回波个数，迭代次数k＝0；

(2)根据信噪比SNR以及参数a，b将S中较小的奇异值置零并记为S₁；

(3)根据信噪比SNR以及参数a，b计算出正则化因子α，然后将测得信号Y、信号矩阵A以及单位矩阵I代入零阶正则化方法公式求解T₂谱X得：X＝(A^TA+αI)^-1A^TY；

(4)判断X中是否有负值，若无负值则输出非负解X，算法结束；否则判断迭代次数k是否达到次数上限k_max；

若k≤k_max，即迭代未到上限，则将求解得到的T₂谱X中的负值置零，得X′，计算Y＝AX′转(5)；

若k>k_max，即迭代到了上限，则转(6)；

(5)利用将信号矩阵A进行奇异值分解得到的矩阵U、S、V以及更新后的矩阵Y更新T₂谱X：迭代次数k＝k+1，转(4)；

(6)将X中的所有负值置零，输出非负解X。

本发明技术方案的优点和积极效果为：

1)能够有效的提高奇异值分解算法求解精度

传统的奇异值分解算法在信噪比较低的情况下得到的T₂谱精度较差。本发明针对奇异值分解算法精度高度依赖初始解的特点，引入正则化方法提供初始解，可以很大程度上提高算法的计算精度。

2)解决低信噪比、布点数较多情况下T₂谱末端非零问题

传统算法在信噪比较低且布点数较多的情况下容易出现末端非零现象。本发明引入正交匹配追踪算法求取T₂谱非零值范围，然后再在非零值范围内求解问题，可以很大程度上解决末端非零的问题。

附图说明

图1为T₂谱反演流程图；

图2为奇异值分解算法反演结果；

图3为正则化方法改进后的奇异值分解算法；

图4为OMP算法改进后的SVD算法。

具体实施方式

下面结合附图以及具体实施方式进一步说明本发明。

1、基于奇异值分解法的改进算法

本发明中求解线性方程组部分使用基于奇异值分解法的改进算法。线性方程组离散模型可以写为：Y＝AX+ε；式中Y为n×1维矩阵，其表示测量得到的自由感应衰减信号，n是回波个数；X为m×1维矩阵，其表示待求的T₂谱，m为弛豫分量数；A为n×m维矩，其表示阵信号矩阵；ε为n×1维矩阵，其表示测量到的噪声信号。

算法使用正则化方法求取问题初始解，然后用奇异值分解算法进行非负迭代。因为奇异值分解算法精度高度依赖初始解精度，而正则化方法可以根据数据信噪比得到比较精确的初始解。因此改进后的算法求解精度会得到很大的提高。

1.1、奇异值分解算法

奇异值分解(SVD)法是一种求解线性方程组的基本方法。假设回波数为n，弛豫分量为m。它首先对信号矩阵A_n×m做奇异值分解，即存在n×n维的正交矩阵U和m×m维的正交矩阵V，以及n×m维对角矩阵S，使得：

A_n×m＝U_n×ndiag[ω₁,ω₂,…,ω_k,0,…,0]V_m×m

对信号矩阵A做奇异值分解运算后，线性方程组解可以写为：

$X=Vdiag\[\frac{1}{{\mathrm{\ω}}_1},\frac{1}{{\mathrm{\ω}}_2},...,\frac{1}{{\mathrm{\ω}}_k},0,...,0\]U^{T}Y$

对于病态问题，直接应用上式可能造成解的不稳定。而SVD算法的特别之处在于，将对角矩阵S中相对较小的奇异值置零，可以增加解的稳定性。通过将相对较小的奇异值置零可以降低矩阵A的病态程度，能够使线性方程组得到较稳定的解。同时，将相对较小的奇异值置零也会损失矩阵A的有用信息。因此，SVD算法求解病态问题的关键就是如何选择合适的奇异值保留个数,使得算法能够求取出即稳定又准确地解。线性截断SVD算法使用系数a、b与信噪比SNR来确定奇异值保留个数，其公式如下：

$X=Vdiag\[\frac{1}{{\mathrm{\ω}}_1},\frac{1}{{\mathrm{\ω}}_2},...,\frac{a\×SNR+b}{{\mathrm{\ω}}_1},0,...,0\]U^{T}Y$

根据实验数据可以得到系数a、b与回波数个数n，弛豫分量m的大致关系为：

$a=1+0.05m,b=35\ln m-58+\frac{0.16\×(n-125)}{\sqrt{m}}$

对于非负约束目前有很多种处理方式。首先需要保证反演结果在低信噪比情况下仍然能保持平滑稳定，不会出现剧烈震荡的解，并且解的精度也不会太低。目前线性截断SVD算法可以达到这一要求。另外，一些情况下即使解足够平滑仍会出现一些负值。此时的负值一般会出现在T₂谱曲线的两端，而这些位置的值一般都为零值，因此即使直接将这些负值置零也不会使反演谱与真实谱曲线产生太大的偏差。所以可以采用如下迭代算法来解决非负约束问题，以避免T₂谱曲线出现负值和不连续问题：

(1)对信号矩阵A进行奇异值分解运算，A＝USV^T，迭代次数k＝0；

(2)根据信噪比SNR将S中较小的奇异值置零并记为S₁，代入奇异值分解的结果计算：，迭代次数k＝k+1；

(3)判断X中是否有负值，若无负值则输出非负解X；否则判断迭代是否达到次数上限：

k≤k_max，即迭代未到上限，则将X中的负值置零，得X′，计算Y＝AX′转(2)；

k>k_max，即迭代到了上限，则转(4)；

(4)将X中的所有负值置零，输出非负解X。

1.2、正则化方法

上述算法并不会删除解中负值所对应的A中的相应列，而是令Y＝AX′，因此其对初始解的要求就比较高。当初始解误差较大时，迭代后得到的解误差就会更大，如图2所示。因此需要求解精度相对较高的正则化方法提供初始解。

正则化方法的模型约束条件矩阵选取单位矩阵I时，称为零阶正则化方法,是该方法最简单的形式：

(A^TA+αI)X＝A^TY

正则因子α的选择一定程度上会影响正则化方法的稳定性和精度。而正则因子α受积分核、解的形状、数据的噪声等因素的影响，因此确定最优的α非常困难。尽管一些论文已经在数学上给出了最优的计算方法，但是实际数据处理过程中很难采用。由于信噪比SNR与正则因子α关系最为密切，因此通常采用试验方法建立的正则因子的先验公式，即正则因子α为信噪比的函数：

$\mathrm{\α}\≈{\left(\frac{{\mathrm{\ω}}_1}{a\×SNR+b}\right)}^2$

当采用上述正则因子α的计算公式时，不需要用迭代法寻找最优的正则因子也可以得到很精确的解，解决了迭代寻优方法速度太慢而不实用的问题。但是这种方法仍然会出现解为负值的情况，而直接将负值置零会很大程度上影响算法的精度。因此将正则化方法的初始解与SVD算法的非负迭代结合就能很好的解决SVD算法初始解精度较低的问题。基于正则化方法改进的线性截断SVD算法具体步骤如下：

(1)对信号矩阵A进行奇异值分解运算，A＝USV^T,迭代次数k＝0；

(2)根据信噪比SNR将S中较小的奇异值置零并记为S₁；

(3)根据信噪比SNR计算出正则化因子α，代入零阶正则化方法公式计算得：X＝(A^TA+αI)^-1A^TY；

(4)判断X中是否有负值，若无负值则输出非负解X，算法结束；否则判断迭代是否达到次数上限；

k≤k_max，即迭代未到上限,则将X中的负值置零，得X′，计算Y＝AX′转(5)；

k>k_max，即迭代到了上限，则转(6)；

(5)利用奇异值分解的结果计算迭代次数k＝k+1，转(4)；

(6)将X中的所有负值置零，输出非负解X。

2、基于OMP算法的改进T₂谱反演算法

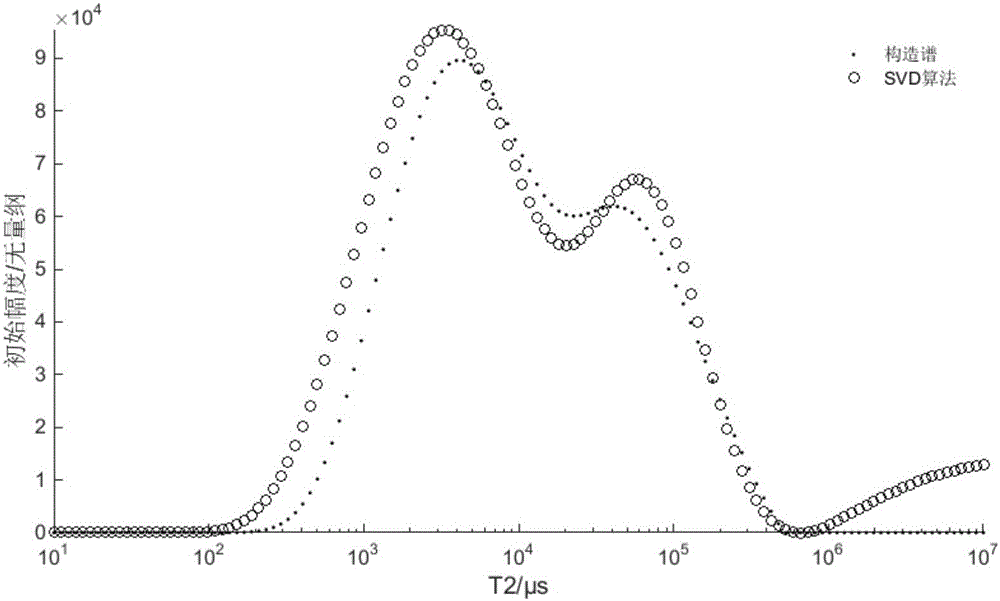
通过上述改进的正则化方法，可以很好的解决SVD算法初始解精度较低的问题。但是对于T₂谱布点数m个数太多时，迭代得到的解会出现末端非零的现象，不能得到很好的解决，如图3所示，因此需要引入正交匹配追踪(OMP)算法。

当T₂谱反演问题弛豫时间分量布点数较多时，其T₂谱首末两端中相当一部分值为零，若不将这些值舍去则会影响T₂谱的形状与解谱精度。因此使用OMP算法选出非零值的范围，然后将范围以外的值置零可以保证解谱的精确度。

假定传感矩阵A的列向量已经做了归一化处理，改进的OMP算法同样需要寻找传感矩阵中与信号最相关的列，然后将其添加进索引集，之后用索引集中的列重构信号矩阵并求出其与原信号矩阵的残差，然后计算带权重的残差，循环迭代直到满足以下约束条件。由于解T₂谱的约束条件为非负，因此终止循环的条件为残差与所有原子的向量积都为负值。算法实现过程如下：

(1)初始化：残差r₀＝Y，索引集V₀＝Φ，权重ω₀＝[1,1,…，1]，迭代次数t＝l；

(2)从传感矩阵A中选出和残差最相关列：

(3)判断＜r_t-1,v_i>是否为负，若为负，则迭代结束，输出索引集V_t；

(4)更新索引集中已选列空间：V_t＝[V_t-1,v_nt]；

(5)利用改进的SVD算法求解线性方程组，并保证解的残差最小，获得的解可以看作Y投影到V_t上的最佳系数，将新得到的解作为V_t各列的稀疏系数值

(6)更新权重：w_t＝w_t-1×weight，weight为值在0.5～2范围内线性排列的向量，其中距n_t位置最近的值为2，最远的值为0.5；

(7)更新带权重的残差：转到步骤(2)。

经过上述步骤后，最终可以得到T₂谱非零值的范围，通过在非零值范围内解谱就可以增加解谱精度。具体来说，就是改进的SVD算法每次非负迭代后都使T₂谱非零值的范围外的值置零，然后继续下一次迭代直到满足停止条件。运行结果如图4所示。

图2是传统的SVD算法反演结果，可以看出反演出的T₂谱精度较差，末端非零现象明显；图3是正则化方法改进后的SVD算法，可以看出反演精度得到明显的提升，但是末端非零现象依然存在；图4是加入OMP算法后的反演结果，可以看出反演精度没有变化，但是末端非零现象得到了很好的解决。