一种无窄谱约束条件下海浪设计波高的推算方法与流程

本发明涉及一种无窄谱约束条件下海浪设计波高的推算方法。
背景技术：
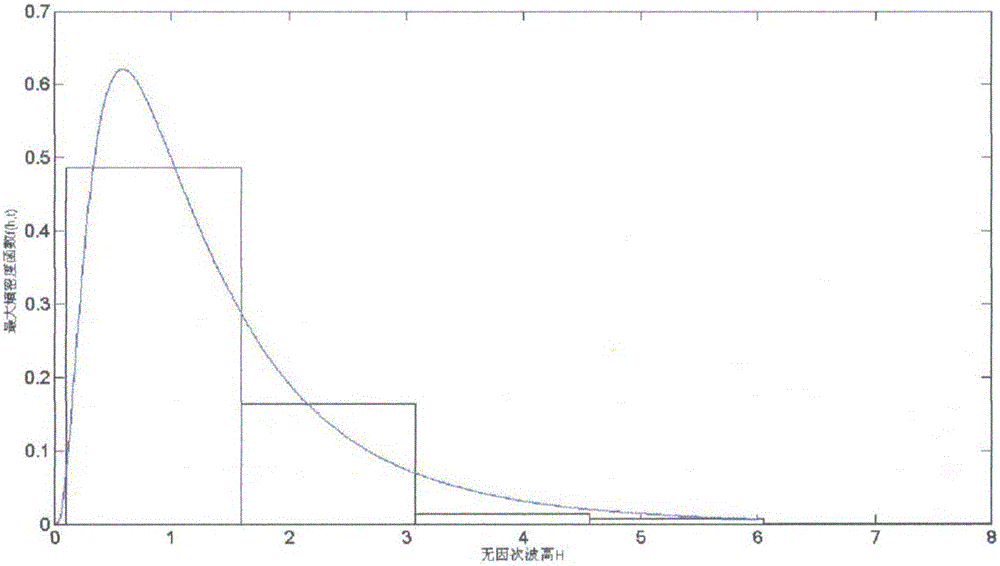
：海浪是发生在海洋中的一种十分复杂而重要波动现象，研究海浪对海洋工程建设、海洋开发、交通航运、海洋捕捞与养殖等活动具有重大意义。而从四十年代以来对海浪的研究已取得了较大的发展。也取得了众多的成果，并且这些成果已经成为了动力海洋学的一部分，与海洋遥感、海洋工程和上层海洋动力学等诸多领域都有密切关系。另外，随着经济技术的发展和国际形势的变化，海浪研究成果对海上军事活动和海上经济的应用价值也越来越重要。目前对海浪的研究内容非常广泛，包括海浪的生成、成长、消衰的过程，以及这些过程中的因素的相互关系。并通过这些过程中的主要因素建立海洋统计学模型和海洋动力学模型来对海浪进行模拟和预报。目前，我国学者在很多方面都都取得了丰硕的成果。包括海浪谱、海浪要素统计分布、海浪预报方法和近岸海浪等方面。海浪研究一般分为两种方法统计学和动力学。在实际研究中往往将两种方法结合。由于海浪具有随机性，所以在实际研究中可以看作随机过程，既可以从海浪的内部结构进行研究也就是海浪谱，也可以从海浪对外表现特征进行研究也就是波要素统计分布。而随机海浪研究的核心问题是对海浪要素的统计分布的研究。对海浪要素的统计分布的研究是从外观方面来研究海浪的随机性质，因此它在海浪的工程应用方面有非常重要的意义，也受到了极大的关注。海浪要素是用来描述海浪的外观随机性质的一些重要的量，如波长、波高、周期等。五十年代以来很多学者开始研究它的统计分布，其研究方法主要可以分为三种，第一种方法是观测实际海浪获得海浪要素数据并对实测数据进行分析，从中找出有关的统计规律。第二种方法是利用实验室设备或电子计算机对海浪进行模拟。第三种方法就是依据海浪理论来寻求海浪要素分布的规律。Longuet-Higgins在1975年首次推导出海浪要素分布函数，此结果是在波面位移为平稳均匀的正态过程和窄谱假定条件下推导的，其结论是海浪要素分布为Rayleigh。由于早期海洋观测技术和观测手段比较落后，使得观测资料不够充分，观测数据不够精确。不能准确的判断实际的海浪要素是否较好地符合这一分布。而随着海洋观测技术的不断发展，通过大量的外海观测和实验室实验反复证明Rayleigh在波面位移是正态过程的假定下对一些问题是良好的近似，如对于深水海浪的描述等。但由于此分布的推导是在假设海浪是正态过程的条件下，因此这就限制了其在一些方面的应用，如对海洋微波遥感和现代海洋军事技术等问题，这就需要对非正态海浪进行研究。由于Longuet-Higgins(1975)导出的海浪分布函数有两个明显的缺点：一是当周期为0时函数值不为0，二是函数关于周期的均值是对称的。而实际海浪要素分布关于周期的均值是非对称的。为了克服上述缺点Longuet-Higgins(1983)通过数学处理又给出了一种关于周期非对称的海浪要素分布。孙孚(1988)根据海浪线性模型和波动的射线理论导出一种新的海浪要素的分布。最近，Stansell等(2004)和Zheng等(2004)对海浪统计理论进行了改进。通过对统计理论作离散化修正的方法推得的分布函数克服了原有理论的一些缺陷。一直以来，虽然对海浪要素分布函数进行不断的改进，但大多数推导结果是以海浪波面位移为正态过程的假定条件下导出的，其结果都是一致的，即海浪要素分布为Rayleigh分布。虽然作此假设使得理论分析和推导大为简化，但是大量的外海观测和实验室实验已经反复证明，实际海浪要素并非都服从Rayleigh分布。Zhang、Xu(2004)基于最大熵原理，通过坐标变换和解一变分问题，导出一种新的海浪波面位移的最大熵概率密度函数，这种密度函数有四个待定参量与以往提出的相比，可以更细致的拟合观测数据和更广泛地适用各种情况下的非线性海浪。而且此函数形式简单，没有弱非线性的限制，从而便于理论和实际应用。技术实现要素：本发明要解决的技术问题是提供一种无窄谱约束条件下海浪设计波高的推算方法。为了解决上述技术问题，本发明采用的技术方案是，一种无窄谱约束条件下海浪设计波高的推算方法，包括波高与周期的联合分布函数和波高与周期的概率密度函数；1)波高与周期的联合分布函数：F(H,T)=e-[(-ln∫0Hαhγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θ---(1)]]>2)波高与周期的概率密度函数：f(H,T)=e-[(-ln∫0Hαhγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θlnθ-1(∫0Hαhγe-βhndh+∫0Tatbe-ctddt)∫0Hαhγe-βhndh·∫0Tatbe-ctddt·[(-ln∫0Hαhγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]2/θ-2+[(-ln∫0Hαhγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θ-2·αHγe-βHn·aTbe-cTd---(2)]]>在式(1)和式(2)中：H：海浪波高T：海浪周期α：待定常数β：待定常数γ：待定常数θ：1≤θ＜+∞n：待定常数a：待定常数b：待定常数c：待定常数d：待定常数h：海浪波高变量t：海浪周期变量。本发明的有益效果是：波高周期的联合分布函数是一种新的非线性的，不是以正态过程和窄谱为条件导出的分布，在一定的物理意义下反映了海浪要素的不确定性。并利用实测数据对联合分布进行验证，并与以往的波高与周期联合分布加以比较。然后应用新的波高周期联合分布推算联合设计值并与传统的联合分布进行比较。结果表明，新的分布函数与实测数据拟合较好，且应用此分布函数推算的联合设计值较安全，能更广泛的应用描述一般的海浪波高和周期，为海洋工程提供理论依据。附图说明下面结合附图和具体实施方式对本发明作进一步详细的说明。图1是本发明实施例的实测波高与周期的散点图。图2是本发明实施例的无因次波高的概率密度函数。图3是本发明实施例的无因次周期的概率密度函数。图4是本发明实施例的波高正态检验的概率图。图5是本发明实施例的周期正态检验的概率图。图6是本发明实施例的波高和周期的联合分布图。图7是本发明实施例的波高和周期的联合分布的等值线图。图8是本发明实施例的不同周期条件下海浪波高的条件分布图。图9是本发明实施例的不同海浪波高条件下周期的条件分布图。具体实施方式一、基于最大熵原理的海浪要素统计分布由于以往的方法都是以波面位移为平稳均匀的正态过程和窄谱假定条件下推导的。其结论是海浪要素分布为Rayleigh。而大量的观测和实验证明实际的海浪要素并非是Rayleigh分布的。因此本实施例在最大熵原理的基础上，导出一种新的周期分布，此分布放宽了限制条件，不再受正态过程和窄谱的限制，并且满足最大熵原理，能在一定程度上反映周期的不确定性，其应用可以更加的广泛。然后本实施例通过分析波高和周期的相关关系，以及波高和周期满足的概率分布模式之间的相关结构关系，利用Copula函数，导出一种新的波高周期的联合分布函数。这种分布函数是一种新的非线性的，且其单变量的分布都满足最大熵原理，在一定的物理意义下能够反映海浪要素的不确定性。下面介绍推导过程：1.1基于最大熵原理的海浪周期分布周期是主要的海浪要素之一，在海洋工程中具有重要的作用。从五十年代起，人们对海浪周期进行了大量的半经验半理论的研究，但目前能被普遍采用的周期分布的理论结果并不多。本实施例利用最大熵原则，导出一种新的周期分布。海浪周期T看成取有限值的非负连续随机变量，即0＜T＜+∞其信息熵为H(T)=-∫0+∞f(t)lnf(t)dt---(1.01)]]>其中f(t)为T的密度函数。显然满足约束条件∫0+∞f(t)dt=1---(1.02)]]>并且，f(t)也应受如下约束：∫0+∞f(t)lntdt<+∞---(1.03)]]>∫0+∞tξf(t)dt<+∞---(1.04)]]>其中ξ为一常数。而约束(1.03)和(1.04)并非先验指定的。式(1.03)反映关于T的一个一般事实：当t→0或t→+∞时，都有f(t)→0；在实际中T总是取正有限值，式(1.04)也符合客观事实。当ξ取整数时，式(1.04)可表示为：T‾=∫0+∞tξf(t)dt<+∞,m=1,2,...---(1.05)]]>即T的任意阶统计矩都存在。按最大熵原理，要找到在式(1.02)，式(1.03)和式(1.04)约束下使得H(T)最大的f(t)。这就转变成了一个条件变分问题。将式(1.01)看成一泛函：H(T)=-∫-∞+∞F(t,y)dt---(1.06)]]>其中y＝f(t)，F(t，y)＝ylny根据变分广义等周问题的定理(沈永欢等2001)有以下推论，在条件(常数)，i＝1，2，…，n(1.07)约束下，H(T)取极值时y(t)函数满足的Eular方程为将式(1.02)、式(1.03)、式(1.04)三个约束条件代入式(1.08)所示的Eular方程便有∂∂f[-fln(f)+λ(f-1)+bfln(t-)-ctdf]=0---(1.09)]]>其中f＝f(t)，而λ，b，c和d为待定常数。由式(1.09)解得的周期在上述三个约束条件下的最大熵概率密度函数的形式为f(t)=atbe-ctd---(1.10)]]>其中a＝eλ-1为待定常数。式(1.10)为周期T的最大熵概率密度函数。用T分布矩可以求得式(1.10)中的参量。其表达式为Γ2(b+2d)Γ(b+1d)Γ(b+3d)=A12A2Γ(b+2d)Γ(b+4d)Γ2(b+3d)=A1A3A22c=Γd(b+2d)[A1Γ(b+1d)]da=dcb+1dΓ(b+1d)---(1.11)]]>其中Amm＝1，2，3，在实际中可由估计。xi为X的第i个观测值。代表Am的估计值。1.2基于单变量最大熵分布的波高-周期的联合分布1.2.1Copula函数联合分布函数包含变量两方面的信息，一是变量边缘分布的信息，二是变量之间相关结构的信息。与单变量分布函数相比，联合分布函数能够更好的描述随机向量的性质。设随机向量(X，Y)联合分布函数为F(x，y)，则X和Y的边缘分布分别为F1(x)＝F(x，+∞)和F2(y)＝F(+∞，y)。在联合分布中除去边缘分布的信息后，就剩下了相关结构函数即Copula函数的信息了。存在函数C使得F(x，y)＝C(F1(x)，F2(y))(1.12)则称C是分布函数F的Copula函数。定理1.1(Sklar定理)设随机向量(X，Y)的联合分布函数为F，F1和F2分别为边缘分布函数，则存在一个相关结构函数C，使得F(x，y)＝C(F1(x)，F2(y))，-∞≤x，y≤+∞(1.13)成立。如果F1和F2是连续分布函数，则C是唯一的；反之，如果C是一个相关结构函数，两个一元分布函数分别为F1和F2，则由式(1.13)定义的函数F(x，y)是一个以F1和F2为边缘分布的二元联合分布函数。由Sklar定理，可将联合分布拆成一元边缘分布和Copula的积。f(x,y)=∂F(x,y)∂x∂y=∂C(F1(x),F2(y))∂x∂y=∂C(u,v)∂u∂v=c(u,v)f1(x)f2(y)---(1.14)]]>其中，f1(x)，f2(y)是边缘分布，c(u，v)是Copula函数C(u，v)的密度函数。几种常用的二维Copula函数及其适用性如下：(1)Gumbel-Hougaard(GH)Copula：c(u，v)＝exp{-[(-lnu)θ+(-lnv)θ]1/θ}，其中θ∈[1，+∞]；GHCopula函数仅适用于变量存在正相关的情形，主要刻画随机变量间的上尾相关性。(2)ClaytonCopula：c(u，v)＝(u-θ+v-θ-1)-1/θ，其中θ∈[0，+∞]；同GH函数，ClaytonCopula适用于描述正相关的随机变量，主要用来描述联合分布中随机变量间的下尾相关性。(3)Ali-Mikhail-Haq(AMH)Copula：c(u，v)＝uv/[1-θ(1-u)(1-v)]，其中θ∈[-1，1)；AMH函数能够描述正或负相关的随机变量，但不适用于正相关或负相关性很高的变量，AMHCopula结构呈对称性。(4)FrankCopula：其中θ∈R；与AMHCopula函数类似，但对相关性程度没有限制。FrankCopula结构具有对称性，即在其分布的上尾和下尾，变量间的相关性呈对称增长。1.2.2基于单变量最大熵分布的海浪波高与周期的联合分布海浪波高概率密度函数为f(H)=αHγe-βHn---(1.15)]]>由于海浪波高为非负的随机变量所以其分布函数可以表示为：F1(H)=∫0Hf(h)dh=∫0Hαhγe-βhndh---(1.16)]]>相应的式(1.10)所对应的周期的分布函数为：F2(T)=∫0Tf(t)dt=∫0Tatbe-ctddt---(1.17)]]>根据实验数据可以得到海浪波高和周期的相关性，且根据散点图可以看出海浪波高和周期的尾部相关性，在不同的情况下选择不同的相关结构函数，来得到其联合分布函数。若实测数据验证海浪波高和周期是正相关的随机变量，且其散点图联合分布中波高和周期具有下尾相关性。符合Clayton相关结构函数的特点和使用范围，以F1(H)和F2(T)为波高和周期的单变量分布，取Clayton相关结构函数为两个边缘分布的连接函数，Clayton相关结构函数形式为：c(u，v)＝(u-θ+v-θ-1)-1/θ(1.18)对上式求导可得到C(u，v)的密度函数，即C(u,v)=∂C(u,v)∂u∂v=(1+θ)u-θ-1v-θ-1(u-θ+v-θ-1)-1θ-2---(1.19)]]>令u=F1(H)=∫0Hαhγe-βhndh---(1.20)]]>v=F2(T)=∫0Tatbe-ctddt---(1.21)]]>将式(1.20)和式(1.21)代入式(1.18)可得到波高与周期的联合分布函数，即F(H,T)=[(∫0Hαhγe-βhndh)-θ+(∫0Tatbe-ctddt)-1]-1/θ---(1.22)]]>要的得到波高和周期的概率密度函数可以先将式(1.20)和式(1.21)代入式(1.19)得到C(u，v)的密度函数为c(u,v)=(1+θ)(∫0Hαhγe-βhndh)-θ-1(∫0Tatbe-ctddt)-θ-1·[(∫0Hαhγe-βhndh)-θ+(∫0Tatbe-ctddt)-θ-1]-1θ-2---(1.23)]]>然后把式(1.15)和式(1.23)代入式(1.14)即可得出波高与周期的概率密度函数为f(H,T)=(1+θ)(∫0Hαhγe-βhndh)-θ-1(∫0Tatbe-ctddt)-θ-1·[(∫0Hαhγe-βhndh)-θ+(∫0Tatbe-ctddt)-θ-1]-1θ-2]]>·αHγe-βHn·aTbe-cTd---(1.24)]]>若实测数据验证海浪波高和周期是正相关的随机变量，且其散点图联合分布中波高和周期具有上尾相关性。符合Gumbel-HougaardCopula相关结构函数的特点和使用范围，同样以F1(H)和F2(T)为波高和周期的单变量分布，取Gumbel-HougaardCopula相关结构函数为两个边缘分布的连接函数，Gumbel-HougaardCopula相关结构函数形式为：C(u，v)＝exp{-[(-lnu)θ+(-lnv)θ]1/θ}(1.25)对上式求导可得到C(u，v)的密度函数，即c(u,v)=e-[(-lnu)θ+(-lnv)θ]1/θlnθ-1(u+v)uv{[(-lnu)θ+(-lnv)θ]-2/θ-2+[(-lnu)θ+(-lnv)θ]1/θ-2}---(1.26)]]>令海浪波高和周期的单变量分布为：u=F1(H)=∫0Hαhγe-βhndh---(1.27)]]>v=F2(T)=∫0Tatbe-ctddt---(1.28)]]>将式(1.24)和式(1.25)分别代入式(1.22)可得到波高与周期的联合分布函数，即F(H,T)=e-[(-ln∫0Hahγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θ---(1.29)]]>然后把式(1.27)，式(1.28)和式(1.26)代入式(1.14)即可得出波高与周期的概率密度函数为：f(H,T)=e-[(-ln∫0Hahγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θlnθ-1(∫0Hahγe-βhndh+∫0Tatbe-ctddt)∫0Hahγe-βhndh·∫0Tatbe-ctddt]]>·[(-ln∫0Hahγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]2/θ-2+[(-ln∫0Hahγe-βhndh)θ+(-ln∫0Tatbe-ctddt)θ]1/θ-2·αHγe-βHn·aTbe-cTd---(1.30)]]>由此方法通过分析波高和周期的相关关系，以及最大熵波高和最大熵周期单变量分布之间的相关结构得到新的海浪波高与周期的分布，此方法不受平稳均匀的正态过程和窄谱假定条件的限制，且边缘分布都是在最大熵原则下推导的，故在一定的物理意义下能更好的反映海浪的不确定性。二、海浪波高与周期的联合分布的检验及应用经过前面对模型的推导及其理论介绍，我们可以通过实测数据来对新的波高与周期的联合分布进行检验。验证其合理性，并与以往的波高和周期的联合分布进行比较。本实施例以朝连岛海域实测海浪波高和平均波高资料(1963-1989)、以及周期和平均周期资料(1963-1989)来对新联合分布进行分析及应用。2.1单变量(波高、周期)的分布函数首先给出海浪无因次波高和无因次周期序列(下简称波高和周期)的数据散点图(图1)。波高和周期的边缘分布分别选用式(1.13)和式(1.14)所示的分布，分布函数分别为：F1(H)=∫0Hαhγe-βhndh---(2.01)]]>F2(T)=∫0Tatbe-ctddt---(2.02)]]>通过式(1.23)和式(1.8)可以求得其相应的参数，见表1。表1波高和周期分布函数的参数值将表1的参数代入式(1.12)和式(1.07)可以得到波高和周期的最大熵概率密度函数(如图2和图3)分别为f(H)=65.4215H-10.2738e-0.1338H5.6174---(2.03)]]>f(T)=0.9651T11.2852e-0.3649T6.4199---(2.04)]]>由图2和图3可以看出，基于最大熵原理导出的波高、周期的概率密度函数与实际数据符合较好。由于以往的概率密度函数都是在正态过程的假设下推出的，由波高和周期的正态检验的概率如图4和图5可以看出波高和周期在很大范围内是不符合正态分布的。2.2海浪波高和周期的联合概率分布对于海浪的研究中，由于不同的海浪要素之间存在一定的相关关系，若只单纯考虑波高或者周期来研究其特性，是不能全面的了解复杂的海浪要素的一些统计性质。因此，同时考虑波高与周期即其联合分布才能更好的掌握海浪的一些特性，从而为海岸工程设计提供合理的依据。本实施例所研究的波高和周期的联合概率密度函数不依赖于正态过程和窄谱的限制条件，且满足最大熵原理，在理论上讲可以更好的描述海浪要素的不确定性。2.2.1海浪波高和周期的相关性及其度量对于海浪要素，其特征变量波高和周期之间存在着一定的相关性。通常用Kendall秩相关系数τ来进行相关性的度量。Kendall秩相关系数τ的计算式为：τ=2n(n-1)Σ1≤i≤j≤nsign[(xi-xj)(yi-yj)]---(2.05)]]>式中：(xi，yi)为实测点数据，sign(□)为符号函数，当(xi-xj)(yi-yj)＞0时，sign＝1；当(xi-xj)(yi-yj)＜0时，sign＝-1；当(xi-xj)(yi-yj)＝0时，sign＝0。n为系列长度。根据黄海某水文站的观测数据，由式(2.05)可以求出波高和周期的Kendall秩相关系数τ＝0.0102。2.2.2Copula函数参数估计及波高和周期的联合分布常用的Copula函数的参数估计方法有相关性指标法、IFM估计法、极大似然法以及适线法等。本实施例采用相关性指标法对Copula函数的参数进行估计。相关性指标法为利用Copula函数的参数θ与Kendall秩相关系数τ之间的关系来计算参数θ。根据式(2.06)可以得出参数θ与τ的具体关系式。τ=4∫01∫01C(u,v)dC(u,v)-1---(2.06)]]>把τ＝0.0102代入式(2.06)，可计算得四种Copula函数的参数。由式(2.10)可计算得到离差平方和，见表2。表2Copula函数的参数及拟合检验OLS(离差平方和)计算结果函数名GumbelClaytonAMHFrank参数θ1.01032.20560.85956.7852离差平方和OLS0.4150.3260.5280.476为了选择拟合效果较好的Copula函数，采用离差平方和进行拟合检验，由表2可以看出，Clayton函数的离差平方和最小，即Clayton函数对于海浪波高和周期之间的拟合效果最好。并且由实测数据验证海浪波高和周期是正相关的随机变量，且其散点图(图1)可以看出联合分布中波高和周期具有下尾相关性，符合Clayton相关结构函数的特点和使用范围。因此从理论上和从经验上讲，应选取Clayton函数对海浪波高和周期的联合分布进行分析计算，即式(1.22)所示的波高和周期的联合分布函数。将表1波高和周期分布函数的参数值及Copula函数的参数θ代入式(1.21)和式(1.19)得到海浪波高和周期的联合概率密度函数为：f(H,T)=3.2056(∫0H65.4215h-10.2738e-0.1338H5.6174dh)-3.2056·(∫0T0.9651t11.2852e-0.3649t6.4199dt)-3.2056·[(∫0H65.4215h-10.2738e-0.1338H5.6174dh)-2.2056+(∫0T0.9651t11.2852e-0.3649t6.4199dt)-2.2056-1]-2.4534·65.4215H-10.2738e-0.1338H5.6174·0.9651T11.2852e-0.3649T6.4199---(2.07)]]>及相应的分布函数为：F(H,T)=[(∫0H65.4215h-10.2738e-0.1338H5.6174dh)-2.2056+(∫0T0.9651t11.2852e-0.3649t6.4199dt)-2.2056-1]-0.4534---(2.08)]]>波高和周期的联合分布及等值线见图6和图7所示采用离差平方和准则进行以正态过程和窄谱条件下推导的波高与周期联合密度函数即式f(α,τ)=πα24vτ2(1+eπα2v2τ)exp{-πα24[1+1v2(1τ-1)2]}---(2.09)]]>和本实施例推导的基于单变量最大熵的波高与周期联合密度函数式的拟合优度比较。离差平方和OLS的计算式如下OLS=1nΣi=1n(pei-pi)2---(2.10)]]>其中，pei为经验频率；pi为理论频率。由式(2.10)计算出两种联合分布的OLS值及其参数见表3和表4表3基于单变量最大熵的波高与周期联合分布的参数及OLS值表4式(2.09)所示的波高与周期联合分布的参数及OLS值VOLS0.40.672由图6和图7可以看出基于单变量最大熵的波高与周期联合密度函数对实测数据的拟合良好。且根据离差平方和与以正态过程和窄谱条件下推导的波高与周期联合分布进行比较，由表3和表4可以看出本实施例推导的基于单变量最大熵的波高与周期联合分布离差平方和较小。在一定程度上显示了其优越性。2.2.3应用新的联合分布函数推算波高和周期的联合重现期海浪波高H和周期T的单变量分布函数分别为式(2.01)和式(2.02)，分别记为F(H)和F(T)，根据Copula函数的定义，海浪波高和周期等于或大于某给定值的波高和周期的单变量重现期为：NH=11-F(H)---(2.11)]]>NT=11-F(T)---(2.12)]]>其中，NH，NT分别为波高和周期的单变量重现期。若给定条件周期T≥t时，海浪波高H的条件概率分布为：FH/T=P(H≤h|T≥t)=P(T≥t|H≤h)P(H≤h)P(T≥t)=(1-P(T≥t|H≤h))P(H≤h)P(T≥t)=P(H≤h)-P(T≥t|H≤h))P(H≤h)P(T≥t)=F(H)-F(H,T)1-F(T))---(2.13)]]>给定条件海浪波高H≥h时，周期T的条件概率分布为：FT/H=P(T≤t|H≥h)=P(H≥h|T≤t)P(T≤t)P(H≥h)=(1-P(H≥h|T≤t))P(T≤t)P(H≥h)=P(T≤t)-P(H≥h|T≤t))P(T≤t)P(H≥h)=F(T)-F(H,T)1-F(H))---(2.14)]]>由式(2.13)和式(2.14)可以给出海浪波高与周期不同组合情况下条件概率图，如图8和图9。从图中可以看出不同周期取值下的海浪波高的概率值以及不同海浪波高取值下的周期概率值(见表5)。表5不同周期取值下的海浪波高的概率值从表5可以直观的看出不同周期条件下波高取值的概率，如：给定条件周期T≥2时，P(H≤1，T≥2)＝0.5613，P(H≤2，T≥2)＝0.8449，可以为海洋工程提供重要的理论依据。波高和周期的联合分布函数为式(2.08)，记为F(H，T)。其海浪波高和周期的联合重现期计算式为：NH,T=11-C(F(H),F(H,T)=11-F(H,T)---(2.15)]]>通过式(2.11)和式(2.12)求得单变量波高和单变量周期相应的5、10、20、50、100、200、500年重现期时波高和周期的值，并根据式(2.15)可以得到其对应的联合重现期(见表6)。表6单变量分布的重现期及其对应的联合分布的重现期由表6可以看出，当波高和周期分别为4.74和2.17时，海浪波高和周期的单变量重现期均为100年，而联合重现期为50.79年。也就是说海浪波高和周期的联合重现期小于其单变量分布的重现期。从设计值的角度描述，相同重现期，单变量波高分布和单变量周期分布推算的设计值小于波高和周期联合分布推算的设计值。在式(2.15)中联合分布函数分别为本实施例推出的联合分布函数式(2.08)和传统的联合分布函数式(2.09)，可求得5、10、20、50、100、200、500年联合重现期时波高和周期的值(见表7)。表7两种分布函数的波高和周期的联合重现水平由表7可以看出，相同重现期条件下，传统联合分布函数式(2.09)推得的波高周期的重现水平小于本实施例推出的最大熵联合分布函数推得的重现水平。即从实际海洋工程设计的角度考虑，传统的方法过低的估计了波高和周期的联合重现水平，从而降低了其安全性。上述结果表明，无论是单变量波高或周期推算的设计值还是传统的联合分布推得的设计值都偏小，因此以安全角度来考虑，以新的海浪波高和周期的联合分布函数推得的设计值更加的安全，可以为海岸工程的设计提供理论依据。以上所述的本发明实施方式，并不构成对本发明保护范围的限定。任何在本发明的精神和原则之内所作的修改、等同替换和改进等，均应包含在本发明的权利要求保护范围之内。当前第1页1 2 3