一种控制受限航天器交会控制系统的线性反馈全局镇定方法与流程

本发明航天器交会控制系统的控制器设计方法。

背景技术：

航天器交会对接是实现航天器维修、拦截、入港，多航天器大规模组装，多卫星网络化协作，以及航天员营救等相关航天任务的基础。航天器交会对接的成功直接影响上述任务的实现。针对航天器交会系统的控制器设计有着重要的工程意义。

由于安装在追赶飞行器上的推力器只能提供有限的推力，从而只能产生有限的控制加速度。如果控制器设计时不考虑这一问题，推力器需要产生的加速度有可能大于推力器本身能够提供的最大加速度。此时，实际闭环系统将不会按照期望的规律进行工作，这不但会降低实际控制系统的控制品质，甚至会导致闭环系统的不稳定性，造成灾难性的后果。

控制受限情形下航天器交会对接系统的控制器设计问题，已经得到了大量国内外科学家的研究，取得了一些不错的结果。利用这些现有控制方法设计的控制律一般有两种形式：一是非线性控制律，其缺点是控制律的实现比较复杂，难以调试；二是线性控制律，其缺点是只能保证闭环系统的局部稳定性(部分线性控制律可实现半全局镇定)。截止到目前，实现全局镇定的线性控制律尚无相关成果报道。

技术实现要素：

本发明是为了解决控制受限情形下的航天器交会控制系统的设计问题，而提出的一种控制受限航天器交会控制系统的线性反馈全局镇定方法。

一种控制受限航天器交会控制系统的线性反馈全局镇定方法按以下步骤实现：

步骤一：引入目标航天器轨道坐标系o-xyz，其原点o位于目标航天器的质心，x轴沿着圆轨道半径的方向，y轴沿着追踪航天器飞行的方向，z轴指向轨道平面外与x轴和y轴构成右手坐标系；基于C-W方程描述的x-y平面内的航天器交会系统的线性化模型，当x与y轴方向上的推力器都工作时，建立实现全局镇定的线性反馈控制律：

u＝FX(1)

其中是状态向量，其中x和分别是x轴方向的位置和速度，y和分别是y轴方向的位置和速度；u＝[u₁,u₂]^T是输入向量，其中u₁和u₂分别是推力器在x与y轴方向上产生的归一化加速度；n是目标航天器的轨道角速度；δ₁和δ₂分别是推力器在x与y轴方向上的能够产生的最大加速度；参数k₁,k₂,k₃,k₄,k₅满足如下条件：

其中

步骤二：对步骤一中得到的控制律(1)，建立保证闭环系统具有最快收敛速率的条件；

步骤三：基于C-W方程描述的z轴方向上的航天器交会系统的线性化模型，建立实现全局镇定的线性反馈控制；

其中是状态向量，z,分别是z轴方向的位置和速度；u₃是推力器在z轴方向上产生的归一化加速度；δ₃是推力器在z轴方向产生的最大加速度；f₁是任意非负常数；f₂是任意正常数。

发明效果：

本发明针对控制受限情形下的航天器交会控制系统提出的控制方法的最显著优点有三个方面。首先，所提出的控制律是线性的，方便设计和实现。其次，闭环系统的全局渐近稳定性得到保证。最后，给出了最优的参数以保证闭环系统具有最快的收敛速度。通过对典型的航天器交会控制系统进行仿真，并与现有方法相比较，结果表明所提出的控制方法能很快完成交会任务，控制性能远远优于现有的控制方法。此外，在仿真研究中，由于所设计的线性控制器直接作用于真实的航天器交会非线性模型之上，所以仿真结果还表明本发明提出的控制方案对线性化误差具有较强的鲁棒性。

附图说明

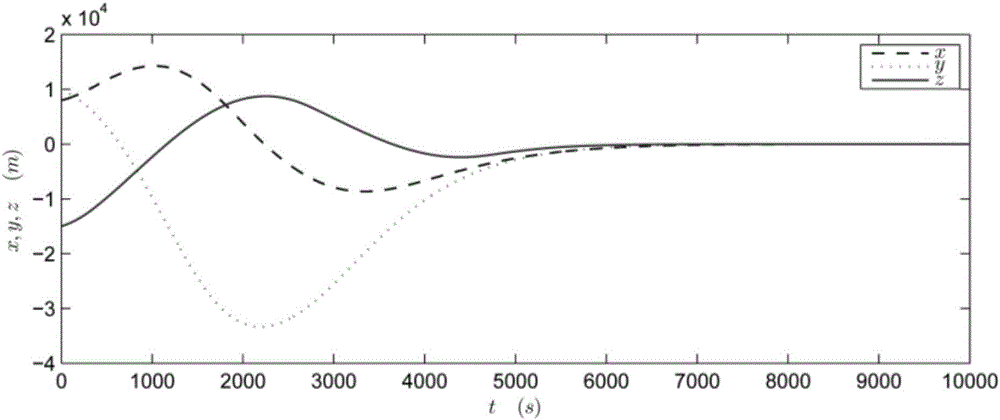
图1为航天器交会系统在本发明所提控制律作用下的位置信号曲线图；

图2为航天器交会系统在本发明所提控制律作用下的速度信号曲线图；

图3为航天器交会系统在本发明所提控制律作用下的控制信号曲线；

图4为航天器交会系统在不同控制律作用下的位置信号曲线图；

图5为航天器交会系统在不同控制律作用下的速度信号曲线图。

具体实施方式

具体实施方式一：一种控制受限航天器交会控制系统的线性反馈全局镇定方法包括以下步骤：

步骤一：引入目标航天器轨道坐标系o-xyz，其原点o位于目标航天器的质心，x轴沿着圆轨道半径的方向，y轴沿着追踪航天器飞行的方向，z轴指向轨道平面外与x轴和y轴构成右手坐标系；基于C-W方程描述的x-y平面内的航天器交会系统的线性化模型，当x与y轴方向上的推力器都工作时，建立实现全局镇定的线性反馈控制律：

u＝FX(1)

其中是状态向量，其中x和分别是x轴方向的位置和速度，y和分别是y轴方向的位置和速度；u＝[u₁,u₂]^T是归一化输入向量，其中u₁和u₂分别是推力器在x与y轴方向上产生的归一化加速度，n是目标航天器的轨道角速度；δ₁和δ₂分别是推力器在x与y轴方向上的能够产生的最大加速度；参数k₁,k₂,k₃,k₄,k₅满足如下条件：

其中

步骤二：对步骤一中得到的控制律(1)，建立保证闭环系统具有最快收敛速率的条件：

步骤三：基于C-W方程描述的z轴方向上的航天器交会系统的线性化模型，建立实现全局镇定的线性反馈控制；

其中是状态向量，z,分别是z轴方向的位置和速度；u₃是推力器在z轴方向上产生的归一化加速度；δ₃是推力器在z轴方向产生的最大加速度；f₁是任意非负常数；f₂是任意正常数。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一中建立实现全局镇定的线性反馈控制律的具体过程为：

步骤一一：系统模型的建立；

采用线性C-W方程作为航天器交会控制系统的数学模型，其具体形式为：

其中a_x,a_y,a_z分别是安装在追赶航天器上的推力器在x,y,z三个坐标轴上产生的加速度，为饱和函数；

σ_δ(·):R→[-δ,δ]是标准的饱和函数，具体形式为

为了简化说明，后文令σ(x)表示σ₁(x)。

航天器交会过程描述为状态向量从非零的初值φ(t₀)转换到状态φ(t_f)＝0的过程，t₀表示交会任务开始时刻，t_f代表交会任务完成时刻；由公式(4)得到航天器交会控制系统在x-y平面内的控制与在z轴方向上的控制是完全解耦的，因此可以对他们分开进行设计。

对于x-y平面内的航天器交会控制系统，其方程为：

分别选取状态向量X和归一化输入向量u如下：

则公式(5)写成如下状态空间的形式：

其中A,B是常数矩阵，形式如下：

步骤一二：闭环系统模型的变换；

对于公式(1)和公式(6)构成的闭环系统，引入线性变换χ＝TX，其中矩阵T形式如下：

由于：

因此T是一个非奇异阵，则在此变换之下，交会模型(6)重写为：

其中：

控制律(1)写成如下形式：

闭环系统为：

步骤一三：闭环系统全局稳定性的检验；

选择半正定矩阵P₀：

定义下述正定对角矩阵：

选取如下Lyapunov函数：

其中f_i代表F₀的第i行，V(χ)＝0当且仅当下面三个式子同时成立时：

χ^TP₀χ＝0,ρ₁χ^Tf₁^Tf₁χ＝0,ρ₁χ^Tf₂^Tf₂χ＝0 (16)

由于k₂>0，所以ρ₁>0,ρ₂>0；观察矩阵：

计算矩阵(17)的各级顺序主子式如下：

由上式可知P₀+F₀^TF₀>0，满足(18)式的χ只能为0，所以V(χ)是正定函数，从而是合适的Lyapunov函数。

Lyapunov函数V(x)沿着闭环系统(12)的时间导数为：

不等式σ^T(u)T₀(u-σ(u))≥0，式中T₀为任意半正定矩阵，令：

则下式成立：

计算：

由于k₄满足式(2)，上面的矩阵S₀是正定的，综合式(21)，由式(19)可得：

由LaSalle不变集原理可知，状态向量会收敛到集合Ξ＝{x:F₀x＝0}中，在集合Ξ中闭环系统(12)变为：

由

矩阵对(A₀,F₀)对任意μ≥0均是可观测的，集合Ξ中唯一的元素是0，因此，闭环系统(12)是全局渐近稳定的。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一至二之一不同的是：所述步骤二中建立保证闭环系统具有最快收敛速率的条件的具体过程为：

由于闭环系统(1)与(6)(或者(12))是全局渐近稳定，因此在有限时间后系统会工作在线性区，成为线性系统。此时系统的收敛速度取决于系统的极点集合λ(A+BF)的位置：

λ(A+BF)＝λ(nA₀+nB₀F₀)＝nλ(A₀+B₀F₀) (26)

其中λ(A₀+B₀F₀)与角速度n无关，使闭环系统具有最快的收敛速度，反馈增益F₀是下述极值问题的最优解：

λ(A₀+B₀F₀)与μ相关；即使在μ给定的情况下，上述极值问题也是一个很难求解的非线性非凸优化问题。这里只给出它的一个局部最优解。

x与y方向上推力器配置相同，则μ＝1；在如下区间：

通过线性搜索，求得式(29)的一个局部最优解为：

(k₁,k₂,k₃,k₄,k₅)＝(0.61,2.97,2.17,5.7138,1.21) (29)

闭环系统的线性化系统的特征值集合为：

nλ(A₀+B₀F₀)＝n{-1.5015±0.3125i,-1.5079±0.1372i} (30)

其它步骤及参数与具体实施方式一至二之一相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是：所述步骤三中建立实现全局镇定的线性反馈控制的具体过程为：

步骤三一：建立航天器交会系统在z轴方向上动力学方程；

由C-W方程描述的航天器交会控制系统(4)可知，x-y平面内动力学方程与z轴上动力学方程是解耦的；因此，由式(4)可知航天器交会系统在z轴方向上动力学方程为：

取系统的状态向量Z与控制向量u₃的形式如下：

则公式(31)用如下系统描述：

Φ,Ψ的形式如下：

步骤三二：

引入下述状态变换：

则公式(33)变为以下形式：

的具体形式如下：

同时控制器(3)的形式变为：

u₃＝H₀ζ,H₀＝[-f₁ -f₂] (38)

闭环系统写成：

步骤三三：闭环系统全局稳定性的检验；

选取如下正定矩阵：

Q₀满足等式再选取如下Lyapunov函数：

其中可以看出W(ζ)是正定的，是合适的Lyapunov函数；令Π₀＝1，则：

Lyapunov函数W(ζ)沿着闭环系统(39)的导数为：

由于矩阵对(Φ₀,H₀)对于任意的f₁≥0,f₂>0均为可观测的，由LaSalle不变集原理可知闭环系统(39)是全局渐近稳定的。

其它步骤及参数与具体实施方式一至三之一相同。

实施例一：

假设目标航天器的轨道高度为500km，轨道半径为R＝6.8781×10⁶m。设

δ₁＝δ₂＝8×10^-3m/s²,δ₃＝6×10^-3m/s²

即μ＝1。对于z轴方向上的控制器(3)，取f₁＝f₂＝5，此时闭环系统的极点集合为λ(Φ₀+Ψ₀H₀)＝{-2,-3}。对于x-y平面内的控制器(1)，其中的参数选择为(29)；

直接针对航天器交会控制系统的原始非线性方程

进行仿真，这里

设初始条件为

闭环系统的状态响应曲线和控制曲线分别记录在图1、图2和图3上。

从图1和图2可以看出，闭环系统的交会完成时间为t_f1＝8000s≈1.4T_p，这里T_p是目标航天器的轨道周期；另外，从仿真结果还可看出，在该控制律的作用下，在初始时刻执行器都是饱和的。这说明闭环系统呈现出本质的非线性特征。此外，用于控制器设计所用的线性化模型(4)和仿真所用的非线性模型(44)是明显不同的，所以仿真结果还说明本发明所提出的控制方案对线性化误差具有较强的鲁棒性。

最后，将本发明所提出的控制律与文献[B.Zhou,Q.Wang,Z.Lin and G.Duan,Gain scheduled control of linear systems subject to actuator saturation with application to spacecraft rendezvous,IEEE Transactions on Control Systems Technology,Vol.22,No.5,pp.2031–2038,2014]中提出的线性增益调度控制律和文献[B.Zhou,N.G.Cui and G.Duan,Circular orbital rendezvous with actuator saturation and delay:A parametric Lyapunov equation approach,IET Control Theory&Applications,Vol.6,No.9,pp.1281-1287,2012]中提出的线性半全局镇定控制律相比较，仿真结果如图4和图5所示。从此两图可以看出，本发明提出的控制律的控制效果远远优于上述文献中报道的两种控制方法。