一种基于状态空间分解的线性约束估计方法与流程

本发明属于具有线性约束的系统状态估计领域，涉及一种基于状态空间分解的线性约束估计方法。

背景技术：

状态估计在信号处理、自动控制和经济领域都有广泛的应用，其主要用于处理非线性问题(比如，扩展卡尔曼滤波，无味滤波，粒子滤波估计)。这些非线性滤波器基本没有考虑到状态约束问题。然而，现实中许多动态系统的状态变量都要求满足许多约束条件，例如，信号有最大幅值，汽车有最大可达到的速度，因此需要开发出一种方法，该方法能够实现线性约束的估计。

技术实现要素：

本发明的目的在于克服上述现有技术的缺点，提供了一种基于状态空间分解的线性约束估计方法，该方法能够实现线性约束估计。

为达到上述目的，本发明所述的基于状态空间分解的线性约束估计方法包括以下步骤：

1)设定随机线性离散时间系统，再使用mmse准则进行线性约束状态的估计；

2)对单个时间点进行状态空间分解，再根据步骤1)设定的随机线性离散时间系统及状态空间分解的结果重构具有线性约束状态的系统模型；

3)计算无约束sigma点的传播函数；

4)对于受约束系统，sigma点被限制于约束域内，即当sigma点不服从步骤2)重构的具有线性约束状态的系统模型时，则将sigma点投影到约束域的边界上，再根据步骤3)计算得到的无约束sigma点的传播函数得区间约束下的sigma点，然后设定区间约束下sigma点的权重，得约束无味点传播函数，然后根据约束无味点传播函数及步骤2)重构的具有线性约束状态的系统模型进行基于状态空间分解的线性约束估计。

设随机线性离散时间系统为：

xk+1＝fkxk+wk(1)

zk＝hkxk+vk(2)

其中，及分别为k时刻的系统状态及量测；fk及hk为线性函数的已知矩阵；及为互不相关的过程噪声及量测噪声，及与xk独立；

设线性约束条件为：

其中，ck为约束矩阵，ck为行满秩的，表示任一约束域；

设f1及f2属于borel域，且对于随机变量y，则有

e[e(y|f2)|f1]＝e(y|f1)(4)

令rk＝ckxk，则有

设b^k＝{bi,i＝1,…,k}为k时刻的事件序列，由式(4)得使用mmse准则的线性约束状态的估计为：

其中，rk在e(xk|rk,b^k-1,z^k)条件下是随机且无约束的。

步骤2)中对单个时间点进行状态空间分解的具体操作为：

对于单个时间点的状态空间分解，则有矩阵为行满秩的，即rank(c)＝m<nx，则有非齐次等式的解为：

cx＝r(6)

其中，r为一个任意给定且具有预设维数的向量；

矩阵c的奇异值分解为：

其中，t表示转置，u及v为正交矩阵，为对角且非奇异的，通过式(7)的奇异值分解可以将式(6)修改为：

则式(6)的一个解xr为：

xr＝v1σ^-1u^tr

在矩阵c的零空间中增加一个的解分量，令使其满足cs＝0，则式(6)的一个特解x为

x＝v1∑^-1u^tr+v2s(8)。

根据步骤1)设定的随机线性离散时间系统重构具有线性约束状态的系统模型的具体操作为：

将式(8)代入到式(1)及式(2)中，得

由式(10)得具有线性约束状态的系统模型为：

其中，

步骤3)中无约束sigma点的传播函数为：

步骤4)中区间约束下sigma点的权重为：

其中，

步骤4)中约束无味点传播函数为：

其中，dyn(uk-1)表示动态模型。

本发明具有以下有益效果：

本发明所述的基于状态空间分解的线性约束估计方法在具体操作时，先重构具有线性约束状态的系统模型，再计算无约束sigma点的传播函数，然后基于无约束sigma点的传播函数计算约束无味点传播函数，最后根据约束无味点传播函数及重构的具有线性约束状态的系统模型进行基于状态空间分解的线性约束估计，操作简单，方便，计算的复杂度较低，估计精度高，能够较好的解决线性约束状态的估计问题。

附图说明

图1为仿真实验中sigma点的演化图；

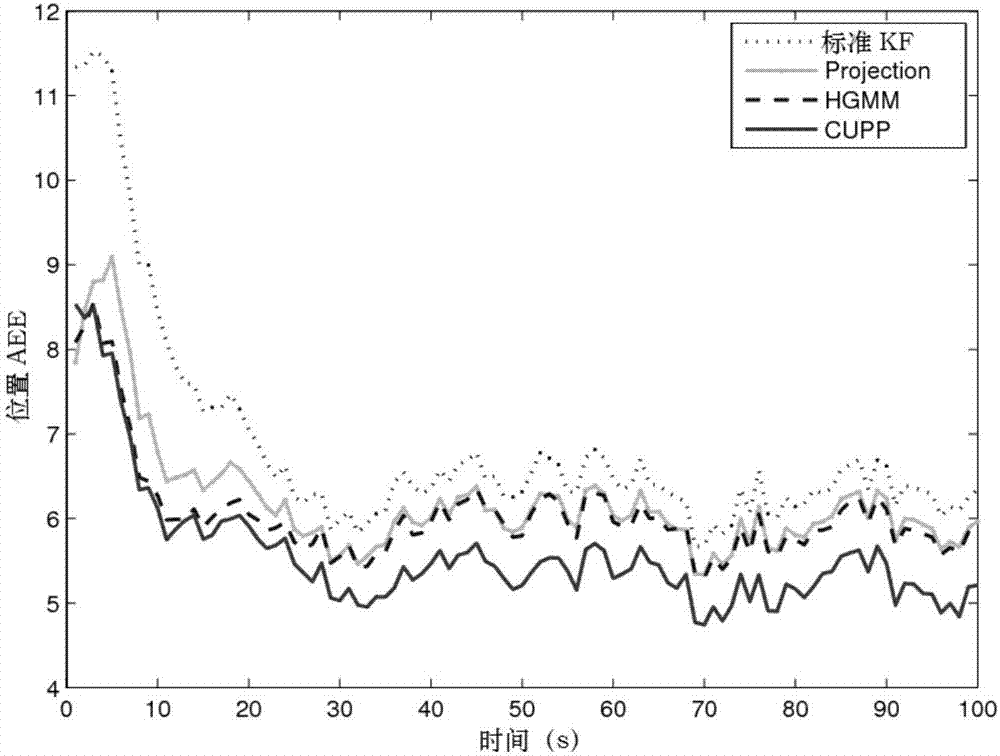
图2为仿真实验中位置的aee比较图；

图3仿真实验中速度的aee比较图。

具体实施方式

下面结合附图对本发明做进一步详细描述：

本发明的基于状态空间分解的线性约束估计方法的具体操作过程为：

1)问题描述

11)设随机线性离散时间系统为：

xk+1＝fkxk+wk(1)

zk＝hkxk+vk(2)

其中，及分别为k时刻的系统状态及量测；fk及hk为线性函数的已知矩阵；及为互不相关的过程噪声及量测噪声，及与xk独立。

对于上述随机线性离散时间系统，我们的目的在于寻找一个基于合适标准的，以所有可用量测序列为条件的xk的滤波估计；本发明选择mmse作为估计准则。

12)线性约束状态

设线性约束条件为：

其中，约束矩阵为行满秩的，即，rank(ck)＝m<nx；表示任一域约束，其中，对约束则有当域约束集中在一个点，则为确定的向量，则式(3)会退化为线性等式约束；当约束为具有合适维数的任意域，则线性等式约束和线性不等式约束可以被认为是式(3)的特殊情况；最后，约束矩阵ck、约束以及系统矩阵fk和hk允许是时变的。

设f1及f2属于borel域，且对于随机变量y，则有

e[e(y|f2)|f1]＝e(y|f1)(4)

令rk＝ckxk，则有

设b^k＝{bi,i＝1,…,k}为直到k时刻的事件序列，由式(4)得使用mmse准则的线性约束状态的估计为：

其中，rk在e(xk|rk,b^k-1,z^k)条件下是随机且无约束的。

2)基于状态空间分解的模型重构

2.1)状态空间分解

对于单个时间点的状态空间分解，则有矩阵为行满秩的，即rank(c)＝m<nx，则有非齐次等式的解为：

cx＝r(6)

其中，r为一个任意给定的具有预设维数的向量。

矩阵c的奇异值分解为：

其中，t表示转置，u及v为正交矩阵，为对角且非奇异的，通过式(7)的奇异值分解可以将式(6)修改为：

则式(6)的一个解xr为：

xr＝v1σ^-1u^tr

在c的零空间中增加一个的解分量，令使其满足cs＝0，则式(6)的一个特解x为

x＝v1∑^-1u^tr+v2s(8)

2.2)系统模型重构

将式(8)带入式(1)及式(2)中，则有

由式(10)得具有线性约束状态的系统模型为：

其中，

当为确定性向量，则为已知的，在线性高斯条件下，当给定式(11)及式(13)，则mmse估计e(sk|r^k,z^k)可以通过标准的卡尔曼滤波推导出。

3)约束无味点传播(cupp)方法

31)由式(5)及式(8)得线性约束状态的mmse最优估计为：

通过有限集近似充分地张成约束状态空间，得

rk及sk的条件期望可以通过式(17)及式(18)近似得到，其中，

式(18)中无约束状态sk被边缘化，可以由卡尔曼滤波最优估计得到；受约束的状态rk可以使用基于仿真的最优滤波器进行估计；

32)无味点传播：

设rk的一般线性动态模型为：

rk＝φk-1rk-1+ξk-1uk-1+wk-1(19)

其中，表示状态，及uk-1分别为白过程噪声和已知输入；φk-1及ξk-1表示具有合适维数的系数矩阵，为解释r从时刻k-1到k的演化，本发明使用ut来处理这个过程，具体的，首先，确定性地选择一套加权点或sigma点，以便可以完全捕获随机变量真实的均值和方差，参考表1所示；

表1

其中，α和β为尺度参数，nr和nw分别为rk-1和wk-1的维数。表示矩阵[·]的任意平方根矩阵的第i列，wⁱ为与第i个点相关的权，例如令则每一个sigma点通过式(20)进行传播，其中，

其中，状态r的演化如图1所示。

设按照表1中的方法选择的sigma点集合与rk-1和wk-1的分布有着同样的样本均值和协方差，运用sigma点演化估计的rk的均值及协方差与真实的前两阶矩一致。

从表1可知由于sigma点是对称分布的，则有

sigma点的采样协方差p^r为：

sigma点的采样协方差p^w为：

如果sigma点是通过式(20)传播的，则预测rk的均值估计为：

预测rk的协方差为

33)区间约束无味变换

步骤32)中选择的sigma点不受任何约束，但为了估计受约束的系统，sigma点应该被限制在约束域中，即当某个sigma点不服从式(14)时，则将这个sigma点投影到约束域的边界上，并且相应的权重被改变，对于具有不等式约束的状态估计，根据区间约束无味变换icut方法得sigma点满足

根据式(21)及式(20)得区间约束下sigma点为：

令为向量的第j项，尺度参数为：

其中，

sigma点的权重为：

其中，

将超出约束范围的被传播点投影到约束域的边界上，并且选择投影点为

设约束无味点传播函数为

其中，输入dyn(uk-1)表示动态模型。

则针对式(11)-式(14)，cupp算法的一次循环如表2所示。

表2

实施例一

道路约束地面移动目标跟踪：

地面移动目标可以被强迫在一条道路上，例如，一个桥上，把一个硬约束加于目标位置。一般来说，道路结构是由一系列位置点p及一个相关宽度w联系着的大量组成部分所表示的。第i个组成是由三个参数(pi,pi+1,wi)所定义的一个矩形。

状态向量假定是根据一个已知的马尔科夫模型进行演化的；为了处理地面移动目标跟踪问题，使用“方向过程噪声”的概念，对于偏离道路的目标，标准的运动模型假定这个目标可以在具有相同过程噪声方差的任何方向移动。对于道路上目标，道路约束意味着沿道路比沿着与它正交的方向具有更多不确定性，假定qa是沿道路方向的过程噪声强度，qo为与道路正交方向的过程噪声强度。

由于沿道路方向运动具有更高的不确定性，qa和qo这两个值被赋予qa>qo，由于状态在x-y坐标系中估计，则qa和qo在路上运动模型中需要转换到x-y平面，即

其中，为旋转矩阵，α为从全局坐标系统的x轴到道路方向的角度，ι和j表示矩阵的行下标和列下标。

仿真场景：在本仿真中，考虑地面目标的运动，它的系统模型由式(1)和式(2)给出，且

qa＝1，qo＝0.01，c＝[10-10]，

基于状态空间分解的重构系统模型是可观测得，对于线性约束系统，hgmm算法选择的转移概率矩阵π为：

性能评估：将cupp算法进行仿真，并与混合网格多模型(hgmm)算法和无约束卡尔曼滤波器(标准kf)及投影估计(projection)方法进行比较。

不同估计器的估计性能通过状态估计的平均euclidean误差(aee)进行评价，从性能评估的角度，aee比均方根误差rmse要好。用m表示蒙特卡罗运行的次数，为第i次运行的状态估计误差，则aee定义为

图2和图3给出了200次蒙特卡罗仿真的估计器的位置和速度aee比较。

从图2及图3中可以观察到：1)在四个估计器中，因为没有考虑位置约束，无约束卡尔曼滤波器误差水平最高。2)cupp方法和hgmm方法均优于投影估计方法，主要原因是这两个方法把约束信息包含到了状态的分布中，从而显著提高了估计的精度。3)hgmm估计器对于线性约束系统的估计是一个可行和有效的方法。然而，由先验信息得到的转移概率矩阵(tpm)需要使用者设计，tpm的设计质量直接影响估计器的性能，由图2明显看到cupp方法的估计误差显然低于hgmm方法的估计误差。