一种基于保局PCA的三维点云配准方法与流程

本发明属于三维重建技术领域，尤其涉及一种基于保局pca的三维点云配准方法。

背景技术：

三维激光扫描仪采用激光测距方法，能够高效地获取目标物的三维数据。为了得到物体完整的三维点云数据，需要通过数据配准将不同视角的点云数据转换到同一个坐标系下。三维点云配准是三维重建的重要环节，在逆向工程、计算机视觉等领域均有广泛的应用。点云配准方法分为手动配准、依赖仪器的配准和自动配准。目前自动配准主要分为基于特征寻找对应关系的配准、基于统计学计算刚体变换的配准和迭代计算最小误差的配准3类方法。

基于主成分分析(pca)的配准方法是属于基于特征寻找对应关系的配准方法。该方法主要利用点云数据体积的主轴方向进行配准。可以利用pca算法计算源点云与目标点云的协方差矩阵，根据协方差矩阵求出源点云和目标点云之间的旋转矩阵和变换矩阵。

在处理三维点云时，初始获取的三维点云维数过高，在进行特征提取分析时需要耗费大量的时间。pca利用降维处理的数学方法，把多指标转化为少数几个综合指标，并保持数据集的整体方差结构。考虑到pca的特征矢量具有旋转不变性的特点，基于pca的点云配准算法具有较好的稳定性和效率。但pca点云配准算法在特征提取时只考虑整体结构，无法提取局部结构特征。因此，需要改进pca点云配准算法的局部结构保留特性。

保局投影算法(lpp)，进行线性降维时可以保留数据局部结构。当采样的数据集位于一个嵌入在高维空间中的低维流形上时，lpp算法可以较好地保留数据集的局部结构。可以保留具有复杂纹路结构点云模型的细节纹路，提高点云模型的配准效率和精度。

技术实现要素：

本发明提出了一种基于保局pca的三维点云配准方法，为了保留点云局部特征，采用保局投影lpp的思想，通过k近邻准则构造点云的邻接图及其补图。对邻近点和非邻近点采取不同的处理方式进行特征提取，通过特征矩阵求得转换参数，进行坐标归一化完成配准。

本发明思路为首先使用采用k近邻准则判断得到物体完整的三维点云数据中各点是否相邻近，并且根据k近邻准则生成邻接图和补图，构造权值矩阵；然后采用保局pca算法进行特征提取，求得特征值对应的特征向量并且将特征值从大到小排序，选取排序靠前的r个特征值对应的特征向量构造特征矩阵；最后根据特征矩阵求出转换参数，进行坐标归一化，完成三维点云的配准。

为了实现三维点云配准快速且精准的问题，一种基于保局pca的三维点云配准方法，具体实现过程包括：

1)、使用三维激光扫描仪扫描得到物体完整的三维点云数据，采用k近邻准则判断点云数据中各点是否相邻近，通过k近邻准则生成邻接图和补图，构造权值矩阵，具体步骤如下：(高维空间r^d中的点云数据记为u＝(u1,u2,…,un)，其中，点ui的k-邻域是指集中在点ui周围并与点ui直线距离最短的k个数据点)

①建立空间包围盒，即建立包含所有点云数据的最小长方体空间，边长为xmax-xmin，ymax-ymin，zmax-zmin；

②采用空间单元格法对包围盒进行划分，按三个坐标轴方向将包围盒划分为a×b×c个边长为l的子立方体，a、b、c分别为空间包围盒x、y、z方向上的子立方体数量；并且，计算点ui所在子立方体的索引号，其所在子立方体的三个坐标轴方向的索引号分别为i，j，k；

③在点ui所在子立方体及周围相邻的27(3×3×3)个子立方体中查找点ui的k个邻近点。为点ui建立一个链表，点ui与周围27个子立方体中的点按距离从小到大的顺序存放在链表中，链表中前k个点即为点ui的k个邻近点。如此可以求出每个数据点的k近邻。

④根据k近邻准则建立邻接图f，如果点ui和点uj邻近，则两点之间用边连接。建立图f'，与图f相反，如果点ui和点uj非邻近，则两点之间用边连接。给边赋权值，构造权值矩阵。图f中，邻近点ui和uj的权值sij可以通过式子sij＝exp(-||ui-uj||²/t)得到；非邻近点之间由于没有边相连，可定义其权值sij为0。图f'中，非邻近点ui和uj的权值sij'为1；邻近点的权值sij'为0。

2)采用保局pca算法进行特征提取，使非邻近点在投影空间尽可能分散，又保留点云数据原有的邻近关系，求得特征值对应的特征向量，具体步骤如下：

①结合lpp算法特性，对邻近点使用约束等式，让邻近点投影到低维空间中仍保持较近的距离。因此，保局pca特征提取的优化函数可表示为式子由于邻近点的权值sij'设为0，非邻近点的权值sij'设为1，因此，可使得非邻近点在投影空间中尽可能地被分散。在对邻近点的约束等式中，邻近点的距离越小，sij的值越大，它们对应的低维空间投影vi和vj的距离就越小。因此，高维空间中离得较近的点投影到低维空间中时仍保持近的距离，这样保留了点云数据的局部结构。

②假设w为最优投影方向，通过拉格朗日乘数法计算，该优化问题可转化为广义特征分解问题；然后求出特征值λ(λ1,λ2,…,λm)和对应的标准特征向量矩阵w(w1,w2,…,wm)。

3)将该函数的m个特征值从大到小排列，得到λ1≥λ2≥…≥λr≥…≥λm，w1、w2、…、wr、…、wm是相应的标准特征向量；如果需要保留前r个成分，则保留的百分比计算公式为式子一般选择百分比超过80％就可以代表数据的绝大多数特征。按照百分比公式求出r，则λ1≥λ2≥…≥λr是该函数最大的r个特征值，w1≥w2≥…≥wr是相应的标准特征向量。则高维数据在低维空间中的投影就可以得出。

1)根据特征矩阵求出转换参数，进行坐标归一化，完成三维点云的配准，具体步骤如下：

①设p＝(p1,p2,...,pn),q＝(q1,q2,...,qm)分别为目标点云数据和测量点云数据。对目标点云和测量点云进行矩阵构建，得到点云矩阵；

②对点云p和q分别进行保局pca特征提取，把两个点云的特征向量和相应特征值按特征值从大到小排序；再选取能代表点云主要特征的特征矩阵wp和wq，根据p和q的特征矩阵得到转换矩阵；

③把测量点云中的点坐标通过转换矩阵，变换到目标点云所在的空间坐标系，进行坐标归一化，实现点云配准。

附图说明

图1(a)、图1(b)是bunny模型配准结果，其中，图1(a)配准前点云，图1(b)保局pca配准算法；

图2(a)、图2(b)、图2(c)是杯子模型配准结果，其中，图2(a)配准前点云，图2(b)pca配准算法，图2(c)改进的pca算法图2(d)保局pca配准算法；

图3(a)、图3(b)、图3(c)是杯子模型的2个局部细节，其中，图3(a)pca配准算法，图3(b)改进的pca算法，图3(c)保局pca配准算法；

图4(a)、图4(b)、图4(c)、图4(d)是玩具模型配准结果，其中，图4(a)配准前点云，图4(b)pca配准算法，图4(c)改进的pca算法，图4(d)保局pca配准算法；

图5(a)、图5(b)、图5(c)是玩具模型某个局部细节，其中，图5(a)pca配准算法，图5(b)改进的pca算法，图5(c)保局pca配准算法；

图6为本发明的基于保局pca的三维点云配准方法流程图。

表一是配准误差比较(μm)

表二是配准平均时间比较(s)

具体实施方式

下面结合实例对本发明进行验证其相对于其他算法的优越性。

如图6所示，本发明提供一种基于保局pca的三维点云配准方法，首先使用采用k近邻准则判断得到物体完整的三维点云数据中各点是否相邻近，并且根据k近邻准则生成邻接图和补图，构造权值矩阵；然后采用保局pca算法进行特征提取，求得特征值对应的特征向量并且将特征值从大到小排序，选取排序靠前的r个特征值对应的特征向量构造特征矩阵；最后根据特征矩阵求出转换参数，进行坐标归一化，完成三维点云的配准。

为了验证改进算法的准确性和效率，分别选择三组点云模型，利用matlab进行仿真实验。第一组实验采用经典的bunny点云模型，第二组实验采用普通三维激光扫描仪扫描得到的玩具点云模型，第三组实验采用扫描得到的瓶子点云模型。实验采用了pca点云配准算法、一种基于k-d树优化的icp三维点云配准算法和本文的基于保局pca的点云配准算法。

1)第一组实验对bunny模型点云采用基于保局pca的点云配准算法进行配准，实验结果如图1所示。图1(a)为配准前的初始点云，两个点云分别包含40835个点和40869个点，图1(b)为配准结果。实验结果表明，基于保局pca的点云配准算法能够取的较好的变换参数，将两点云调整到准确的位置，获得较好的配准效果。

2)第二组实验对瓶子模型点云采用三种不同的配准算法进行配准，两个点云分别包含16209个点和16178个点，实验配准结果如图2(a)、图2(b)、图2(c)所示，配准结果的2个局部细节如图3(a)、图3(b)、图3(c)所示。实验结果表明，基于保局pca的点云配准算法与pca点云配准算法、按点云大小给定尺度的改进pca算法相比，配准精度明显提高，模型局部细节的清晰度和完整性有明显的改进。

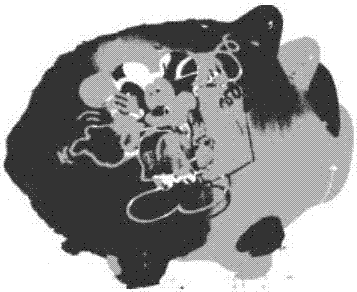
3)第三组实验对一个普通玩具模型点云进行配准，两个点云分别包含25947个点和25869个点，实验配准结果如图4(a)、图4(b)、图4(c)、图4(d)所示，配准结果的某个局部细节如图5(a)、图5(b)、图5(c)所示。实验结果表明，基于保局pca的点云配准算法在局部结构特征保留方面有明显的改进，模型上一些细节复杂的纹路可以更清晰的表示出来，局部细节“米老鼠”图案更加清晰。并且，在获得整体和局部特征同时，能够有效地剔除冗余点和错误的匹配点。

对三种点云配准算法进行误差比较，不同规模点云的配准误差如表1所示。通过表1可以看出，无论模型点云数据的规模多大，按点云大小给定尺度的改进pca算法的配准精度优于pca点云配准算法，基于保局pca的点云配准算法的配准精度优于其他2种配准算法。

对三种点云配准算法进行时间效率分析，三种算法配准的平均时间如表2所示。通过表2可以看出，按点云大小给定尺度的改进pca算法的配准时间最大，说明该算法的配准精度的提高是以牺牲时间效率为代价的，而基于保局pca的点云配准算法的配准时间没有明显的变化。基于保局pca的点云配准算法使用k近邻准则建立邻接图，采用空间包围盒发对空间进行分割，通过建立索引减少了权值矩阵计算时间。

表1

表2。