一种针对结构光成像的多径干扰的解扰方法与流程

本发明属于计算机图像处理领域，具体涉及一种针对结构光成像的多径干扰的解扰方法。

背景技术：

结构光成像属于主动式的三维扫描成像技术，该技术需要投影仪投射一组条纹图案到目标物体上，并利用相机拍摄物体表面产生形变的投影图案。基于这种设计，相机感光阵列中的每个像素在视野范围内只应看到投影机投射出的图案中的一个像素点；然而，也会有例外发生，比如被扫描物体表面具有复杂的几何形状，像阶梯状的边缘这种在深度上具有不连续性的区域，或者物体具有能大量反射来自投影仪的光线类似镜面这样高反射系数的表面，这些情形会导致多径干扰的出现，究其原因是相机感光面上的某像素接收到来自投影仪投影图案上的多个位置发出的光线。而其中的双峰或双模多径干扰指的是，相机感光面上的某像素接收到来自投影仪上的两个位置的光线，例如在物体的阶梯形边缘处，相机上的某些像素可以同时看到阶梯形边缘的两侧，这里称两侧的像素分别为前景像素和背景像素。这种存在于结构光系统中的，除了从投影仪到待测物体再到相机的主光路以外干扰光路所构成的多径干扰，会给最终的重建结果带来严重的误差和畸变。通过对国内外相关技术的调研，可以发现该问题仍未得到很好解决。

基于结构光的三维扫描成像技术，通过将一系列条纹图案投影到目标场景上，并利用相机拍摄的图像来计算目标物体的三维信息。通过计算，采集图片上的每一个像素点都能对应到投影图案上的某一个行。相移键控通常被认为是最简单的结构光测量术之一，其对应的投影图案集合可以表示为：

其中x^p,y^p分别是投影图案中像素的列坐标和行坐标，是投影图案中对应像素的强度，其动态范围为0到1，n表示在总数为n的图案中的相移指数。

对于三维重建而言，相机所拍摄到的图像，是投影出的正弦条纹图案在被扫描的物体表面发生形变后的图像，可以表示为：

其中x^c,y^c分别是像素在相机图像坐标系中的列坐标和行坐标，而是该像素的强度。a^c是整个投影图案集合中的平均像素强度值，表征的是环境光的成分，可根据以下式子导出：

相应地，b^c表示给定像素的调制强度，根据构造出实部和虚部，通过如下公式导出b^c：

其中，

公式(6)表示观测到的正弦条纹的振幅。

如果是一个常量或受投影正弦条纹图案影响较小的量，b^c的值将会接近于零。因此可以通过噪声检测器或是滤波器将b^c值较小的区域在进入后续的进一步处理之前滤除。对于那些b^c足够大的像素，θ表示在采集到的正弦条纹图案中的像素点对应的相位，可由下式得到：

其中j是表征虚部的符号，通过它可以进一步求得投影图案上的行坐标θ＝2πy^p。

为了应对如热噪声等来自投影仪和摄像机的干扰，通常需要在式(2)中引入更高的空间频率：

其中k是投影图像中包含的正弦条纹的数量。如果仅使用高频的扫描图案，在θ的求解过程中会面临取值任意性的问题，这个问题可以通过引入低频率的扫描图案来解决。例如，可以选用k＝1，k＝4和k＝16进行三次单独的扫描，使用k＝1的扫描来解缠k＝4扫描的相位，然后使用当前生成的结果再来解缠k＝16扫描的相位。这种方案引入的噪声量级是k＝1扫描方法的1/16，其中

技术实现要素：

针对现有技术的不足，本发明提供了一种针对结构光成像的多径干扰的解扰方法，包括如下步骤：

步骤1，生成投影图案集合并进行投影；

步骤2，获取被扫描的物体表面发生形变后的投影图案；

步骤3，对两条混叠光路进行分离，完成两次分离的深度测量。

步骤1中，所述投影图案集合表示为其中，

其中x^p,y^p分别是投影图案中像素的列坐标和行坐标；是投影图案中对应像素的强度，其动态范围为0到1；n表示在总数为n的图案中的相移指数。

步骤2中，所述投影出的正弦条纹图案在被扫描的物体表面发生形变后的图像表示为：

其中x^c,y^c分别是像素在相机图像坐标系中的列坐标和行坐标，而是该像素的强度；a^c是整个投影图案集合中的平均像素强度值，b^c表示给定像素的调制强度，θ表示在采集到的正弦条纹图案中的像素点对应的相位。

根据构造出实部和虚部通过如下公式导出b^c：

公式(6)表示观测到的正弦条纹的振幅。

通过如下公式计算θ：

其中j是表征虚部的符号，通过θ能够求得投影图案上的行坐标，即：θ＝2πy^p。

步骤3包括：

步骤3-1，通过添加上标f和b来区分和上的前景和背景成分，对公式(4)和(5)分别简化后得到公式(9)和(10)：

其中，和分别表示的前景成分和背景成分，和分别表示的前景成分和背景成分，

步骤3-2，根据前景矢量和背景矢量来合成相机成像阵列上存在多径干扰的像素的可观测矢量的振幅和相位：

其中ya和yb是形成双峰干扰的两条光路分别对应到原始投影图案上的行坐标，表示两条光路在投影图案上的相位差，k表示频率缩放因子；

步骤3-3，建立优化任务，任务的目标是从观测矢量中分离出待求解的矢量和对所述优化任务进行求解，其中将矢量表示成模和相位角的形式，i是表示相位角的符号。

步骤3-3包括：采用四层循环，分别对四个变量在各自对应搜索空间内循环搜索，寻找满足如下优化目标的最优解：

其中分别表示解出的最优值，λ是权重参数。

步骤3-3包括：

步骤3-3-1，第一阶段：通过如下公式解出和

其中，dy表示两条光路在投影图案上的相位差，和dy在满足优化目标下的最优解分别表示为

步骤3-3-2，第二阶段：以第一阶段解出的和dy为约束，通过最小化下式表示的均方误差来获得绝对相位和

使得且

和在满足优化目标下的最优解分别表示为

步骤3-3-1中，引入一个新的零频率扫描图案，将在k＝0时获得具有最大模值的表示为此时能取得所有频率下的最大值，得到如下公式：

从而得到如下约束关系：

此时沿着的方向在k的所有扫描值上搜索满足(11)式中的均方误差最小的位置，实现对和相位差的穷尽式搜索，得到和dy三个参数的最优解。

步骤3-3-2中，对投影图案的相位和值做一次穷尽式搜索，对在0到2π的范围内搜索，同时将定义成通过一层for循环实现穷尽式搜索，在这层for循环内部，对和进行搜索，并结合第一阶段求解出的最优幅度值和来计算(13)式的均方误差。

提出在结构光扫描仪校准阶段在各扫描频率下计算投影图案上各像素均值的方法，来应对结构光成像系统中受组件光学器件的低通滤波效应的影响，不同空间频率图案的衰减程度不同的问题，以利于观察双峰多径传输下观测信号的振幅随着投影图案空间频率变化形成的非平坦响应。

本发明基于传统的相位轮廓测量术，提出了一种低成本且实用性强的方法，通过参考物理学中的驻波理论，巧妙应用了正弦波的相干干涉和相消干涉这样一个有趣线索来实现两条光路的分离，完成两次分离的深度测量，且不需要对硬件系统做任何改动，也不需要定制任何特殊的投影图案，所以该方法可以很容易的嵌入到现有的结构光系统中去。这里将主要关注点放在双峰多径干扰上，也是基于其重要性的考虑，在基于相移结构光的扫描重建的系统中如果待扫描物体存在阶梯形边缘，就会导致相机传感器上某些像素同时接收到一部分来自上边缘和一部分来自下边缘的光线，从而形成的双峰多径干扰是无法避免的。

除此以外，本发明还解决了结构光成像中特有的一个问题，即受光学镜头低通滤波效应的制约，高空间频率图案在通过光学模组后在信号幅度上的衰减比低空间频率图案更大。在传统的基于结构光成像的相关研究工作中，这一问题很大程度上被忽略了，因为最后求解的相位是由高频率图案决定的，而较低频率的图案只是用于解缠高频图案。本发明通过直接在扫描仪校准阶段构建一个包络函数来解决这个问题，从而更清楚地观察出双峰多径传输下观测信号的幅度随投影图案空间频率变化而产生的非平坦响应。

本研究的创新点如下：第一，研究存在双峰多径干扰的两条光路与投影图案空间频率的交互关系，发现两条光路随着扫描图案频率变化而产生的相干干涉和相消干涉的规律，并提出通过计算两条干扰光路生成的合成光路的振幅随投影频率变化的下的方差来识别存在双峰多径干扰的像素。第二，提出引入零频扫描图案以及两阶段的优化算法，将解扰算法的计算复杂度从o(n⁴)降到o(n²)。零频扫描图案的引入可以计算出双峰干扰的两条光路所生成的合成光路的振幅峰值，并可将其作为参考值，来归一化其他扫描频率下合成光路的振幅。第三，提出在结构光扫描仪校准阶段在各扫描频率下计算投影图案上各像素均值的方法，来应对结构光成像系统中受组件光学器件的低通滤波效应的影响，不同空间频率图案的衰减程度不同的问题，以利于观察双峰多径传输下观测信号的振幅随着投影图案空间频率变化形成的非平坦响应。

附图说明

下面结合附图和具体实施方式对本发明做更进一步的具体说明，本发明的上述或其他方面的优点将会变得更加清楚。

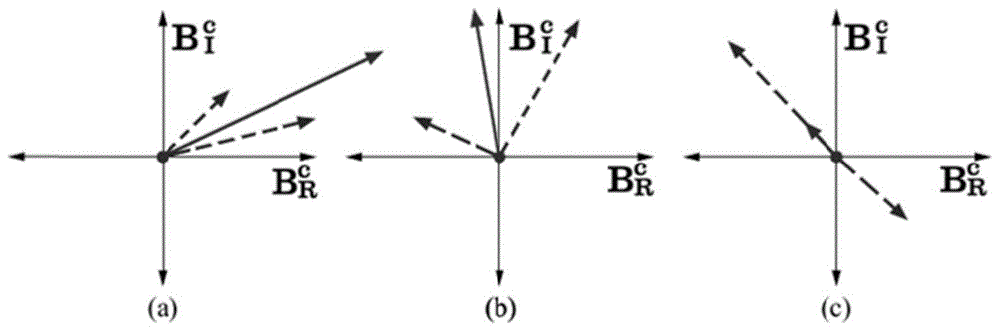
图1是由来自多径传输(虚线)中的前景和背景矢量相加来构造复平面上的可观测的合成矢量(实线)的示意图。随着频率缩放因子的变化(其中(a)k＝0，(b)k＝8和(c)k＝12)，合成向量的方向和长度也会发生相应变化。

图2是可观测的合成矢量的振幅(纵轴)作为缩放因子k(横轴)的函数，其振幅随k取值的变化而变化的示意图。

图3中圆圈表示理想无噪声情况下随着k(对数坐标下)取值变化而变化的图例。图3最上方表示背景像素b，中间表示边缘像素ab，下方表示在连续频率k下的横轴代表k，纵轴代表[0,1]之间的归一化强度。

图4是前景和背景像素之间不同组合比例对合成矢量幅度产生的影响示意图，即表示投影仪图像坐标系上相距12个像素的背景像素，前景像素，在从0.1到0.5，每隔0.2为步长的组合比例调控参数的控制下，所合成的具有双峰干扰的边缘像素幅度随k(对数坐标下)变化的曲线。

图5是前景和背景像素之间的不同间距变化对合成的形状所产生的影响示意图。从上到下，前景和背景像素的距离差距对应归一化到[0,1]之间的相位差分别为0.02，0.42，0.96。

图6是由两块错叠在一起的无纹理的泡沫板所构造出的阶梯形边缘(图6上方的图)中的方差示意图(图6下方的图)。参考图2所示的波形，对每个像素在所有k(对数坐标下)中计算的方差。其中前景像素标记为a，背景像素标记为b，边缘像素标记为ab。

图7是由圆圈表示的真实采集数据的在有限取值的k(对数坐标下)上的变化图示。最上方表示背景像素b，中间表示边缘像素ab，下方表示前景像素a。

图8是由圆圈表示对放置在投影仪有效深度区域中心处的一块白色，无纹理的泡沫板扫描后得到的在k(对数坐标下)的各个取值下对所有像素做平均化之后的波形图。本发明中将其作为系统传递函数的估计值以用作后续扫描时的标准化因子。

图9是由圆圈表示对放置在投影仪有效深度区域中心处的一块白色，无纹理的泡沫板扫描后得到的在k(对数坐标下)的各个取值下对所有像素做平均化之后的波形图本发明中将其作为系统传递函数的估计值以用作后续扫描时的标准化因子。

图10是沿着图6中的阶梯边缘从双峰多径传输中提取出的主要(较强)和次要(较弱)分量的相位的伪彩图。

图11是使用本发明的方法对多径干扰进行解扰之前和之后的对比重建结果。图11左边是未经解扰处理重建出的阶梯边缘的网格表面，图11右边经解扰算法处理后，从图6提取出的主相位分量重建出的阶梯边缘的网格表面。

图12是由一台普通dlp投影仪和一个灰度相机组成的结构光扫描系统。该系统与传统的结构光扫描仪一样，无需在硬件上做任何改造。

图13是实施例中透过聚酯布网以及透明塑料盒子对一个白色猫头鹰雕像进行扫描重建。

图14是在猫头鹰雕像前放置网格的场景的点云重建结果。对应的重建点云显示到正视图即图14最左边，侧视图(图14中间的图)和俯视图(图14右边的图)。其中，图14中上方的图对应使用传统pmp方法的重建结果，中间的图对应使用本方法提取出的主路径的重建结果，下方的图将上方和中间的重建点云同时显示在相同坐标系中。

图15是在透明塑料盒子里放置猫头鹰雕像的场景的点云重建结果。对应的重建点云显示到正视图(即图15左边的图)，侧视图(图15中间的图)和俯视图(图15右边的图)。其中，图15上方的图对应使用传统pmp方法的重建结果，中间的图对应使用本方法提取出的主路径的重建结果，下方的图将上方和中间的重建点云同时显示在相同坐标系中。

具体实施方式

下面结合附图及实施例对本发明做进一步说明。

本发明提供一种基于传统的相位轮廓测量术的双峰多径干扰的解扰方法来实现两条混叠光路的分离，完成两次分离的深度测量。可以运用到各类通过调制正弦信号的相位进行测量的系统中去。

信号处理领域中，通常为了简化模型，人们往往假设对原始模拟信号的采样是在极小的一段时间内进行的，但事实上，通过仪器设备采集到的信号都是在一段固定的时间间隔内的平均值。同理，在数字相机中，感光阵列上的每个像素都会在水平方向和垂直方向对应一定角度范围内采集光线。相机感光阵列上某像素在其视野范围内，可以同时观测到一部分前景和一部分背景。通过添加上标f和b来区分和上的前景和背景成分，可以进一步简化得出下面两个方程：

在这里通过添加上标f和b来区分和上的前景和背景成分。

需要注意的是，将pmp条纹图案的空间频率增加k倍会在保持正弦条纹振幅恒定的同时，相位也会随之增加相等的尺度。在多径传输的情况下，这种频率缩放化关系如图1所示。图1左边展示的是单位频率的前景和背景分量，而图1中间和图1右边展示的是当k＝8和k＝12时的前景和背景分量。图1中的虚线矢量分别表示由和以及和构成的复向量，而实线矢量表示由和叠加形成的合成矢量。

通过频率缩放因子k的引入，可以控制前景和背景矢量的方向/相位按相同的缩放比例进行变化，这一过程可以通过图1上围绕原点旋转的矢量来模拟。需要注意的是，通过分别旋转前景，背景矢量，两矢量相加后的合成向量的相位缩放程度很可能不同于之前所述的缩放比例因子，而且合成矢量会在相干和相消干涉之间来回切换。具体来说，当分立矢量方向相同产生相干干涉时，合成矢量的振幅等于各个分立矢量振幅的和值，而当分立矢量方向相反产生相消干涉时，合成矢量的振幅等于各个分立矢量振幅的差值。

在数学上，可以根据前景矢量和背景矢量来合成相机成像阵列上存在多径干扰的像素的可观测矢量的振幅和相位：

其中ya和yb是形成双峰干扰的两条光路分别对应到原始投影图案上的行坐标，表示两条光路在投影图案上的相位差。合成矢量的相位和幅度可以看成是频率k的函数，可以利用其随k的取值变化而发生变化的规律来检测扫描图像中存在的多径干扰。这里的目标是从观测矢量中分离出待求解的矢量和该任务的搜索空间由和这四个独立变量确定，计算复杂度是o(n⁴)。

为进一步减小计算复杂度，本发明提出了如算法所示的两阶段的优化算法，首先解出和以最小化下式的均方误差，

其中，dy表示两条光路在投影图案上的相位差，和dy在满足优化目标下的最优解分别表示为

然后以第一阶段解出的和dy为约束，通过最小化下式表示的均方误差来获得绝对相位和

使得且和在满足优化目标下的最优解表示为

具体来说，在第一阶段的搜索中，为了将由三个独立变量和dy确定的搜索空间进一步减少到两个变量和dy确定的搜索空间，本发明提出引入一个新的零率扫描图案，即在k＝0时获得以至于：

从而得到约束关系：

这样，可以沿着的方向在k的所有扫描值上搜索满足(11)式中的均方误差最小的位置，实现对和相位差的穷尽式搜索。通过这种方式，把第一阶段的算法复杂度从o(n³)减小到了o(n²)，与此同时，将第二阶段的算法复杂度保持在o(n)，因为已经在第一阶段中求解出最优解。总体来说，本方法提出的两阶段的优化算法将整体计算复杂度从o(n⁴)减小到了o(n²)。

综上所述，在和定义的三维空间中执行穷尽式搜索来最小化(12)式定义的误差。这意味着本发明的算法包含有三层for循环，真正意义上的穷尽式搜索是指在for循环从负无穷到正无穷的搜索，然而，投影仪只能在归一化后的0到2π的范围内投影光线，这也意味着dy的变化范围也只能在0到2π区间内，这会限制dy的搜索空间。与此同时，在和上进行的for循环只能从0到因为绝对值符号意味着不需要考虑小于0的数值。在k＝0时，多径传输的两条光路能产生最完美且最强的相干干涉。所以只需要在将简单设置为的情况下，让关于的for循环在0到的范围内搜索，这就减少了对再做一次独立for循环搜索的所需的计算量。

一旦得到了第一阶段的三个参数的最优解，接下来在上述三个最优解的约束下，对投影图案的相位和值做一次穷尽式搜索。这可以通过一层for循环实现，对在0到2的范围内搜索，同时将定义成在这层循环内部，对和在取值范围内进行搜索，并结合上一阶段求解出的最优幅度值和来计算(13)式的均方误差。

实施例

图3的仿真结果中，横轴表示频率k(对数坐标下)，纵轴表示具有双峰多径干扰的合成像素的矢量幅度其中，在投影图案中相距12个像素的(图3上方的图)前景像素，图3下方的图为背景像素，以及由55％前景和45％背景像素线性组合成的存在双峰干扰的边缘像素(图3中间的图)。横轴频率k的变化范围为1到60，以对数形式显示，对应最高频率的波长在投影图案上以8个像素为一个周期。纵轴使用将所有归一化到0和1之间，深色曲线表示的是k从1到60变化范围内利用本发明的方法解出的用来拟合观测值的最优和矢量合成的矢量幅值。

图4进一步阐释了前景和背景像素在不同取值组合比例的控制下，对合成矢量幅度的形状的影响关系。本实施例中仿真了在垂直方向具有480个像素的投影图案上，同样相距12个像素的背景像素和前景像素，在0.1到0.5范围内，每隔0.2为步长的不同组合比例参数的调控下，合成出的具有双峰干扰的边缘像素的幅值这里横轴的数量单位仍然以对数形式来表示。

图5进一步阐释了前景和背景像素之间的距离变化对合成的产生的影响。本实施例中仿真了在垂直方向上具有480个像素的投影图案上，相距不同间距的背景像素和前景像素合成的存在多径干扰的像素幅度值具体来说，前景和背景像素距离差距归一化到[0,1]之后的相位差分别为0.02，0.42，0.96。

本实施例中将两层半厘米厚，无纹理的泡沫板层叠在了一起，以构造出阶梯形的边缘。图6下方的图展示了在该场景中沿着k轴计算出的的方差，其中高亮的垂直线清晰的指出了阶跃边缘所在的位置，即存在严重的双峰多径干扰的区域。为了展示在真实数据上的形状，图7显示了按照图6所标记出的a，b和ab这三个像素在k从1到60的观测矢量的振幅其中a对应边缘右侧的前景像素，b对应边缘左侧的背景像素，ab对应边缘处包含多径干扰的像素。

通过观察图7中的曲线，可以观察到随着横轴频率数值的不断增大，纵轴表示的幅度值会持续下降。这是由投影仪中光学元件的低通特性所造成的效应模糊了投影图案中正弦光栅图案。本发明提出一种有效方案来解决这种与投影仪光学系统的传递函数相关的问题。在投影仪的有效深度区域的中心位置处放置一块白色，无纹理的泡沫板来扫描，然后针对每一个频率因子k，对所有像素的求平均值，结果如图8所示，并将该结果作为后续扫描的标准化因子。将这种标准化因子应用到图7上可以得到如图9所示的结果。该图展示了前景和背景像素a和b上的与预期相一致的平坦响应曲线，以及存在多径干扰的边缘像素ab上的明显的类正弦曲线。图10显示了解出的主光路的振幅(它被定义为或中较大的一个)以及次光路的振幅的相位值。图11展示了通过这种算法解出的主路径的相位值重建出的阶跃边缘上再无双峰多径效应的干扰。

本发明提出在结构光扫描仪校准阶段在各扫描频率下计算投影图案上各像素均值的方法，来应对结构光成像系统中受组件光学器件的低通滤波效应的影响，不同空间频率图案的衰减程度不同的问题，以利于观察双峰多径传输下观测信号的振幅随着投影图案空间频率变化形成的非平坦响应。

为了进一步在结构光系统中演示多径分离的效果，透过一层聚酯布网扫描了一个白色石膏猫头鹰小雕像，图14展示了在使用本发明所提出的多路径检测和解扰方案之前以及之后的相位和点云的对比效果图。图14最上方对应的是基于传统方法解出的相位重建的三维点云图。图14中间部分显示了使用本发明提出的多径检测和解扰方法解出的相位重建的三维点云图。图14最下方的图几通过将两种三维重建结果放置在相同的坐标系中，不难看出，本发明所提出的技术相对于没有该解扰过程的传统方法的改进非常明显。

为了展示针对透明物体带来的多径干扰的解扰效果，图15展示了一只放置在透明塑料盒内的猫头鹰雕像的重建结果。对应的重建点云分别显示到正视，侧视和俯视的角度。其中，图15最上方是使用传统pmp方法的重建结果，图15中间是使用本发明方法提取出的主路径的重建结果，图15最下方将上方和中间的重建点云显示在同一个坐标系中。在这个例子中，在基于传统方法的重建结果中，半透明塑料盒的重建位置错误地出现在和猫头鹰的脸部相近的深度位置上。而利用本发明提出的算法，塑料盒的透明平面重建在了猫头鹰前方正确的位置上。在末行图中，忽略掉透明层的点云干扰，由传统相位重构技术重建的猫头鹰点云与本发明提出的多路径检测和解扰算法重建后的点云仍不能完全重合。

本发明提供了一种针对结构光成像的多径干扰的解扰方法，具体实现该技术方案的方法和途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。