分数阶无刷直流电机系统的自适应混沌控制方法与流程

本发明涉及分数阶无刷直流电机系统，具体涉及分数阶无刷直流电机系统的自适应混沌控制方法。

背景技术：

无刷直流电机，是一种电子驱动的无极变速电机，具有调速性能好、寿命长、维护方便噪声小、功率大、动态响应好等诸多优点，因而在航天航空、机器人等领域得到了一定的应用。然而，无刷直流电机对初始条件存在指数敏感性，吸引子上的动力学表现出混沌运动，其具体表现形式为转速与转矩间歇振荡、控制性能不稳定、伴随产生不规则的噪声等。由此可知，混沌现象极大地影响无刷直流电机系统的稳定性和安全性，因此必须要从控制方法上加以抑制。

分数阶无刷直流电机系统的状态变量并不容易用物理方法量测出来的，有些根本就无法量测；甚至一些中间变量没有常规的物理意义。此种情况下要实现状态反馈，就需要构造状态观测器。即利用待观测系统的可以量测得到的输入和输出信息来估计待观测系统的状态变量，以便用此状态变量的估计值来代替待观测系统的真实状态变量进行状态反馈设计，从而实现闭环系统高性能控制。

随着对分数阶微积分理论研究和应用的不断深入，分数阶微积分理论在分形理论、电介质、储能材料等方面已经得到了很好的应用。在控制理论学科中使用分数阶微积分的优势在于，它能够更加准确的对包含记忆和遗传效应的系统建模。即在复杂动态系统中，应用分数阶微积分方程建模要比整数阶系统模型更加准确，因为分数阶系统模型可以准确描述动态系统的属性特征。分数阶控制器不仅适用于分数阶无刷直流电机系统模型，对于整数阶无刷直流电机系统模型也能充分体现其优越性。

无刷直流电机系统实际电容和实际电感具有分数阶特性，机械惯性也具有分数阶特性。那么包含电感和机械储能的电动机模型也可能实际上是分数阶的，用分数阶模型更能接近电动机的本质。受到不确定因素的影响，包括温度、噪声、测量误差、参数估计误差与器件老化等，分数阶无刷直流电机系统具有高度的不确定性，但其自适应混沌控制复杂，研究的难度大。

技术实现要素：

有鉴于此，本发明的目的是提供一种分数阶无刷直流电机系统的自适应混沌控制方法，降低不确定因素对系统稳定性与可靠性的影响，消除微分项的膨胀从而使控制器和参数设计简单，利用状态变量的估计值来代替待观测系统的真实状态变量进行状态反馈设计，降低对物理传感器的要求，从而实现系统高性能控制。

本发明的目的是通过这样的技术方案实现的，分数阶无刷直流电机系统的自适应混沌控制方法，包括以下步骤：

(1)首先建立无刷直流电机系统的分数阶数学模型，利用状态变量的估计值来代替待观测系统的真实状态变量进行分数阶高增益观测器的设计；

(2)定义误差向量，利用chebyshev神经网络以任意小的误差逼近非线性函数的特性，设计分数阶levant微分跟踪器抑制微分项的膨胀；

(3)利用分数阶李亚谱诺夫函数求解虚拟控制输入与实际控制输入并进行稳定性分析，通过连续频率分布式模型方法在backstepping的框架中构造自适应混沌控制器。

进一步，在步骤(1)中，所述无刷直流电机系统的分数阶数学模型包括两个相互关联的子系统：

其中，τ2＝lq/r，τ3＝ld/r，σ＝n²，ρ＝(1-δ)n²，tl表示负载转距；uq和ud分别表示q轴和d轴定子电压；id，iq，ω，n分别表示d轴电流，q轴电流，转子角速度和永磁极对数；vd表示d轴电压，vq表示q轴电压；j，r，ld，lq分别表示转动惯量，绕组电阻，d轴电感和q轴电感；b，ke，分别表示永磁磁通，粘性阻力系统，永磁磁通常数和附加载荷，α1表示分数阶阶次。

进一步，所述分数阶高增益观测器为：

其中，l＝diag(l,l²)，l表示增益，k3＞0，为状态变量的估计值；表示赫维茨矩阵，y表示系统的输出，表示系统输出的估计值，φ表示chebyshev神经网络的权向量。

进一步，李雅普诺夫函数其中γ1＞0，权重函数v0表示李雅普诺夫函数，ω表示频率；z1(ω,t)、分别表示α1与φ1系统实际状态；

得到

频率分布式模型表示为

定义得到

相应的连续频率分布式模型：

v1(t)的分数阶导数计算为

其中αv2(t)表示虚拟控制输入；

虚拟控制输入为：其中s1＝σ/τ1，表示s1的上界，c1表示控制器参数，q1(t)、q2(t)表示误差变量，ξ1(x)表示chebyshev多项基函数，表示chebyshev神经网络的基函数矢量，表示ζ1(x)的估计值，表示ξ1(x)的转置，k1表示观测器参数，υ1表υ示比例观测器误差，表示chebyshev神经网络的逼近误差；

与虚拟控制输入对应的分数阶自适应律为：其中γ1和m1表示控制器参数，c1＞0，m1＞0；则

进一步，实际控制输入包括q轴的实际控制输入和d轴的实际控制输入，李雅普诺夫函数

其中γ2＞0，权重函数z2(ω,t)、z2(ω,t)分别表示α2与φ2的系统实际状态；

通过计算q2(t)的分数阶导数，得到

所述的分数阶levant微分跟踪器为

其中r1和r2表示正常数，

相应的连续频率分布式模型为：

v2(t)的导数计算为

所述q轴的实际控制输入为：其中c2表示控制器参数，ζ2(x)表示chebyshev多项基函数，表示ζ2(x)的估计值，表示ζ2(x)的转置，k2表示观测器参数，υ2表示比例观测器误差，θ2表示分数阶levant微分跟踪器的实际输出，θ1表示跟踪微分器的虚拟输出；

与q轴的实际控制输入对应的分数阶自适应律为：其中γ2和m2表示控制器参数；则

定义李雅普诺夫函数其中γ3＞0，z3(ω,t)，zφ3(ω,t)分别表示α3与φ3的系统实际状态；

对误差变量q3(t)求分数阶导数

相应的连续频率分布式模型为

求解v3(t)的导数

所述d轴的实际控制输入为：其中c3表示控制器参数，q3(t)表示误差变量，ξ3(x)表示chebyshev多项基函数，表示ζ3(x)的估计值，表示ξ3(x)的转置，k3表示观测器参数，υ3表示比例观测器误差；

与d轴的实际控制输入对应的分数阶自适应律为：其中γ3和m3表示控制器参数；其中c3＞0，m3＞0；

通过变换，得到则

由于采用了上述技术方案，本发明具有如下的优点：

本发明提供的一种分数阶无刷直流电机系统的自适应混沌控制方法，以具有函数未知，虚拟控制微分项的膨胀、混沌振动和状态变量不可测等特征的分数阶无刷直流电机系统为对象，建立无刷直流电机系统的分数阶数学模型，达到准确描述动态系统属性特征的目的，利用状态变量的估计值来代替待观测系统的真实状态变量进行分数阶高增益观测器的设计，降低对物理传感器的要求，定义误差向量，利用chebyshev神经网络以任意小的误差逼近非线性函数的特性，取消了对系统精确数学模型与精准参数的要求，设计分数阶levant微分跟踪器抑制微分项的膨胀进而使控制器和参数设计简单，利用分数阶李亚谱诺夫函数求解虚拟控制输入与实际控制输入并进行稳定性分析，通过连续频率分布式模型方法在backstepping的框架中构造自适应混沌控制器。本发明实现了保证系统瞬态和稳态性能的分数阶无刷直流电机系统的自适应混沌控制，抑制了混沌振动等对分数阶无刷直流电机系统控制性能的影响。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作进一步的详细描述，其中：

图1为无刷直流电机系统；

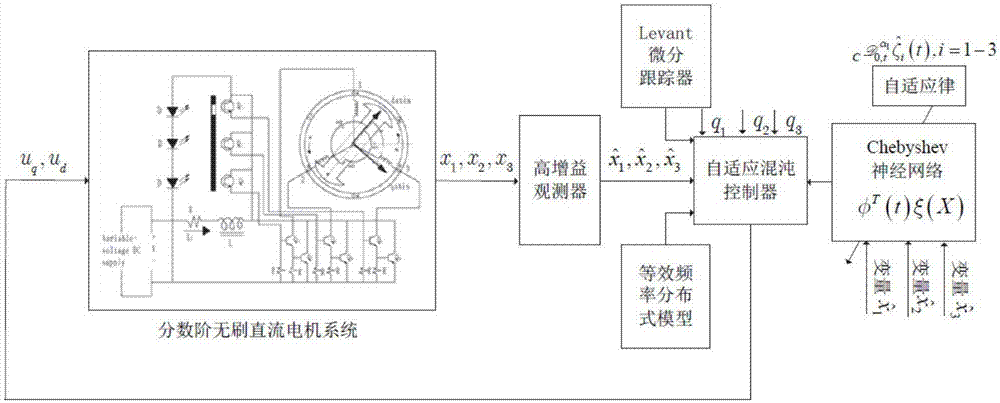
图2为分数阶无刷直流电机系统的自适应混沌控制方法的框图；

图3为无刷直流电机系统的混沌吸引子；

图4为不同分数阶阶次下的无刷直流电机系统混沌吸引子；

图5为分数阶阶次α1＝0.95且参数η扰动下的相图；

图6为在η＝1.6和α1＝0.95下的系统状态变量x1,时序图；

图7为在η＝1.6和α1＝0.95下的系统状态变量x2,时序图；

图8为在η＝1.6和α1＝0.95下的系统状态变量x3,时序图；

图9为在分数阶α1＝0.95且不同η值下的观测器误差e2；

图10为在分数阶α1＝0.95且不同η值下的控制输入uq；

图11为在η＝1.6且不同分数阶值下的变量q2。

具体实施方式

以下将结合附图，对本发明的优选实施例进行详细的描述；应当理解，优选实施例仅为了说明本发明，而不是为了限制本发明的保护范围。

一种分数阶无刷直流电机系统的自适应混沌控制方法，包括以下步骤：(1)首先建立无刷直流电机系统的分数阶数学模型，利用状态变量的估计值来代替待观测系统的真实状态变量进行分数阶高增益观测器的设计；(2)定义误差向量，利用chebyshev神经网络以任意小的误差逼近非线性函数的特性，设计分数阶levant微分跟踪器抑制微分项的膨胀；(3)利用分数阶李亚谱诺夫函数求解虚拟控制输入与实际控制输入并进行稳定性分析，通过连续频率分布式模型方法在backstepping的框架中构造自适应混沌控制器。该方法的具体方法如下：

无刷直流电机系统如图1所示，它属于机电系统，其机电耦合方程可写为

其中id,iq,ω,n分别表示d轴电流(a)，q轴电流(a)，转子角速度(rad/s)和永磁极对数，vd表示d轴电压(v)，vq表示q轴电压(v)，j,r,ld,lq分别表示转动惯量(kgm²)，绕组电阻(ω)，d轴电感(h)和q轴电感(h)，分别表示永磁磁通(wb)，粘性阻力系统(n/rad/s)，永磁磁通常数和附加载荷。

定义τ2＝lq/r，τ3＝ld/r，则公式(1)变为

其中无量纲表示为,ρ＝(1-δ)n²，tl表示负载转距，uq和ud分别表示q轴和d轴定子电压。

当系统参数设置为τ1＝1,τ2＝6.45,τ3＝7.125,uq＝4.017,ud＝-15.305,tl＝2.678,σ＝16,ρ＝1.516和η＝1.6时，无刷直流电机系统出现混沌振荡。图3展示了无刷直流电机系统的混沌吸引子。

为了更加精准的描述无刷直流电机系统的特征与特性，考虑转子角速度，q轴电流和d轴电流的分数阶α1，其分数阶耦合系统可以分解成两个相互关联的子系统：

x1表示在卡普托定义下对x1求α1次导，图4表示在相同条件下不同的无刷直流电机系统分数阶阶次α1＝0.95,0.9,0.8能够使系统的运动由混沌运动转变为规则运动。显然，分数阶无刷直流电机系统具有混沌特征。图5通过相图揭示了分数阶无刷直流电机系统的混沌运动对系统参数η的扰动非常敏感。

为了便于控制器设计，引入分数阶微积分中广泛应用的卡普托定义，其表达式如下

其中表示伽马函数，n表示整数，h⁽ⁿ⁾(t)表示函数h(t)的n阶求导。

对任意连续函数x(t)，下列等式存在

当满足h(0)＝0和0<p,q<1时，等式存在

引理1:当和时，i(t)和o(t)分别表示连续频率分布式模型的输入与输出，非线性分数阶系统可以转换成下列连续频率分布式模型

其中表示权重函数，表示系统实际状态。

chebyshev神经网络

chebyshev神经网络能够以任意精度逼近任何连续函数，chebyshev多项式可以设计为

ti+1(x)＝2xti(x)-ti-1(x),t0(x)＝1(8)

其中x∈r和t1(x)通常定义为x，2x，2x-1或2x+1。

针对x＝[x1,…,xm]^t∈r^m，chebyshev多项式的增强模式由下面构成

ξ(x)＝[1,t1(x1),…,tn(x1),…,t1(xm),…,tn(xm)](9)

其中ti(xj),i＝1,…,n,j＝1,…,m表示chebyshev多项式，n表示阶数，ξ(x)表示chebyshev多项基函数。

未知非线性函数fcnn(x)的估计值可以表示为其中φ(t)表示权向量。定义理想参数矢量φ^*：

其中ωφ和dx分别表示φ(t)和x的界限紧集。

对任意给定常数ε＞0，存在chebyshev神经网络：

定义参数估计误差和任意给定的估计误差其中表示δ(t)的上界。

分数阶高增益观测器设计

对式(3)进行矩阵变换

其中f3(x)＝x1x2/τ3-x3/τ3,ki,i＝1,2,表示赫维茨多项式的系数且有p(s)＝s²+k1s+k2,x＝(x1,x2,x3)。

a表示赫维茨矩阵。对于任意给定的矩阵q^t＝q＞0，存在正定矩阵p^t＝p＞0使得

a^tp+pa＝-2q(13)

受到物理条件的限制，变量x1，x2，x3的信息不可测，因此设计分数阶高增益观测器来在线估计状态变量信息，其表达式如下：

其中i＝diag(l，l²)，l表示增益,k3＞0，

为了便于快速求解，通过如下转换关系从而减少chebyshev神经网络的权向量数目

其中i＝1,2,3。得到

其中表示chebyshev神经网络的基函数矢量，表示chebyshev神经网络的逼近误差，e表示单位矩阵，

定义观测器误差i＝1,2,3和比例观测器误差υi＝ei/l^i-1，i＝1,2和υ3＝e3。从式(12)，(14)和(16)可以得到

表示chebyshev神经网络基函数的估计值，其中

考虑李雅普诺夫函数:

它的分数阶导数可以计算为

可以得到

其中正定常数β＞0，λmax(p)表示p的最大特征值。

从式(13)和(20)可知，(19)重写为

其中λmin(q)表示q的最小特征值。

控制器设计

步骤1:定义误差变量和分数阶李雅普诺夫稳定准则

其中γ1＞0，γ1表示正定常数，z1(ω,t)，分别表示α1与φ1的系统实际状态。

可以得到从引理1可知，连续频率分布式模型表示为

其中s1＝σ/τ1未知，但其上界已知。

在定义后，得到

进而获得等效连续频率分布式模型：

v1(t)的分数阶导数计算为

其中αv2(t)表示虚拟输入控制。

选择虚拟输入控制和相应参数分数阶自适应律

其中控制器参数c1＞0，m1＞0。c1表示控制器参数，q1(t)、q2(t)表示误差变量，ξ1(x)表示chebyshev多项基函数，表示chebyshev神经网络的基函数矢量，表示ζ1(x)的估计值，表示ξ1(x)的转置，k1表示观测器参数，v1表示比例观测器误差，表示chebyshev神经网络的逼近误差。

把式(27)代入式(26)得到

步骤2:考虑李雅普诺夫函数

其中γ2＞0，z2(ω,t)、z2(ω,t)分别表示α2与φ2的系统实际状态；

通过计算q2(t)的分数阶导数，得到

为避免对式(27)进行反复求导，利用基于super-twisting算法的levant微分器来解决这个问题。因此，跟踪微分器中的实际输出θ2可以按下面关系式进行替代

其中r1和r2表示正常数，θ1表示跟踪微分器的虚拟输出。

得到则相应连续频率分布式模型满足

从式(29)和式(32)可知，v2(t)的导数计算为

设计q轴的控制输入和相应的分数阶自适应律为

其中c2＞0，m2＞0，c2表示控制器参数，ξ2(x)表示chebyshev多项基函数，表示ζ2(x)的估计值，表示ξ2(x)的转置，k2表示观测器参数，υ2表示比例观测器误差，θ2表示分数阶levant微分跟踪器的实际输出，θ1表示跟踪微分器的虚拟输出；

把式(34)代入式(33)得到

步骤3:定义和选择李雅普诺夫函数

其中γ3＞0，z3(ω,t)、zφ3(ω,t)分别表示α3与φ3的系统实际状态。

对q3(t)求分数阶导数

从引理1可知，相应连续频率分布式模型表示为

利用式(38)，求解v3(t)的导数

d轴的控制输入和分数阶自适应律设计为

其中c3＞0，m3＞0。c3表示控制器参数，q3(t)表示误差变量，ξ3(x)表示chebyshev多项基函数，表示ζ3(x)的估计值，表示ξ3(x)的转置，k3表示观测器参数，v3表示比例观测器误差；

通过变换，得到对式(39)进行简化得到

定理1:针对分数阶无刷直流电机系统(3)具有未知项、不确定参数、不可测状态和混沌行为等特征，提出由参数分数阶自适应律(27)、(34)、(40)，分数阶levant微分跟踪器(31)和分数阶高增益观测器(14)构成的自适应混沌控制方法能够保证所有分数阶无刷直流电机系统的信号有限，同时相应的混沌行为得到彻底抑制。

证明：定义李雅普诺夫函数

对上式进行求导

其中mmin＝mi，i＝1,2,3。

定义式(43)变为

上式意味着

从式(45)可知系统信号诸如xi,qi,和υi都有界。到此，定理1的证明已经完毕。

通过仿真分析来验证所提分数阶无刷直流电机系统自适应混沌控制方法的有效性。分数阶高增益观测器参数选取为k1＝30,k2＝10,k3＝30,l＝2。跟踪微分器参数选取为r1＝3,r2＝3。自适应混沌控制器参数选取为c1＝8,c2＝8,c3＝10,γ1＝2,γ2＝2,γ3＝2,m1＝1,m2＝1,m3＝1。所有状态变量的初始值设置为零。

图6-8为在η＝1.6和α1＝0.95下的系统状态变量xi,i＝1-3时序图。在30秒钟前分数阶无刷直流电机系统的运动状态处于混沌状态，其时序图处于无规则的高频振荡状态。从30秒开始，自适应混沌控制器介入后，分数阶无刷直流电机系统的运动从混沌状态立即转变为稳定状态。不管分数阶无刷直流电机系统是混沌状态还是稳定状态，分数阶高增益观测器都能以任意小的观测误差逼近真实状态信息。

图9为在分数阶α1＝0.95且不同η值下的观测器误差e2。在自适应混沌控制器没有介入前，随着系统参数η的变化，观测器误差出现一定幅值的波动。一旦自适应混沌控制器介入后，观测器误差立即趋于零，同时不受到系统参数η变化的影响。

图10为在分数阶α1＝0.95且不同η值下的控制输入uq。在30秒前自适应混沌控制器没有介入，其控制输入为零。从30秒钟开始，控制输入经过瞬间峰值后立刻趋于零，同时系统参数η的扰动对控制输入uq的影响忽略不计。

图11为在η＝1.6且不同分数阶值下的变量q2。在30秒之前，当分数阶值发生变化时，q2出现很大的波动。当自适应混沌控制方法介入后，q2快速趋于零，同时分数阶值的变化所导致的影响基本忽略不计。

以上所述仅为本发明的优选实施例，并不用于限制本发明，显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。