量子状态滤波器及相关方法与流程

本发明涉及量子态估计技术领域，尤其涉及一种量子状态滤波器及相关方法。

背景技术

一个n量子位的量子系统的状态密度矩阵ρ是一个在希尔伯特空间里的d×d(d＝2ⁿ)矩阵，具有d×d＝2n×2n＝4n个参数，所以，所要估计的量子态参数的数量是随着n的增长呈指数增加，换句话说，一个标准的量子态估计需要o(d²)次的测量配置。实际实验中人们感兴趣的量子状态往往是纯态或者近似纯态的，此时ρ是一个秩为r低秩的厄米矩阵。利用这一先验信息，人们将由candes、donaho等人在2006年提出的压缩感知理论应用到量子态估计中：先通过一个测量矩阵a，将原始信号投影到低维空间；再通过求解一个优化问题，从少量的测量值中，精确重构出原始信号。压缩感知理论将测量次数减少为ο(rdlogd)。在基于压缩感知的量子态估计中，有两个重要问题需要解决：1)测量次数至少为多少时可以保证所选出的测量矩阵的数据中包含足够多的信息，重构出密度矩阵ρ；2)需要设计一个高效，并且鲁棒性强的重构算法，以便能够以压缩感知理论给出的最小采样率，达到高精度的优化问题的解。

对于问题1)，根据压缩感知相关理论，人们已经得到结论：当测量次数m满足压缩感知所要求的低秩测量矩阵的限制等距性质(restrictedisometryproperty，rip)条件时，就可以使观测矩阵a以很高的概率满足秩rip理论。此时人们可以将测量次数从完备测量的o(d²)减少到o(rdlogd)。

对于问题2)，基于压缩感知的量子态估计的凸优化算法，由于所涉及到的参数维数很大，一般的算法很难有效求解。例如，smith等人将量子态估计问题总结为最小方差(ls)问题，并采用凸优化工具箱求解。但是对于高维量子系统，随着所需要的存储空间的增加，计算时间也随之增加，使得重构难以实现。li首次将交替方向乘子(admm)算法用于求解基于压缩感知的量子态重构问题，获得了较快并且具备鲁棒性的算法。然而在li的算法中，大量的高阶矩阵求逆的运算导致算法花费时间很长，以量子位n＝7为例，在intelxeone5-2407cpu、2核、主频2.4ghz、内存16g的机器上，以92.43％的正确率重构出密度矩阵需要近3个小时的时间。另外，在li所定义的优化问题中，当同时考虑密度矩阵含有稀疏干扰以及测量值中含有噪声情况时，基于该问题的优化算法重构难度加大，效果变差。

技术实现要素：

本发明的目的是提供一种量子状态滤波器及相关方法，极大降低了运算复杂度，同时，在重构出量子状态的同时，估计出稀疏干扰和高斯噪声，并且算法可以更快地找到更精确的解。

本发明的目的是通过以下技术方案实现的：

一种量子状态滤波方法，包括：

获取测量矩阵a和与之对应的测量向量b；

初始化密度矩阵ρ^k、稀疏干扰s^k、高斯噪声e^k、拉格朗日乘子y^k与迭代次数k；

下一次迭代时，基于pj-admm算法将密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k转换为三个子问题并添加近邻项，且结合测量矩阵a和与之对应的测量向量b来更新密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k，进而更新拉格朗日乘子y^k；

根据当前迭代次数来判断是否满足停止条件；

若满足停止条件，则保留最终更新得到的密度矩阵、稀疏干扰、高斯噪声及拉格朗日乘子。

一种量子状态滤波器，包括：

测量矩阵与测量向量获取模块，用于获取测量矩阵a和与之对应的测量向量b；

初始化模块，用于初始化密度矩阵ρ^k、稀疏干扰s^k、高斯噪声e^k、拉格朗日乘子y^k与迭代次数k；

更新模块，用于下一次迭代时，基于pj-admm算法将密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k转换为三个子问题并添加近邻项，且结合测量矩阵a和与之对应的测量向量b来更新密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k，进而更新拉格朗日乘子y^k；

判断模块，用于根据当前迭代次数来判断是否满足停止条件；

量子状态保留模块，用于在满足停止条件时，保留最终更新得到的密度矩阵、稀疏干扰、高斯噪声及拉格朗日乘子。

由上述本发明提供的技术方案可以看出，一方面，针对带有稀疏干扰和高斯噪声的量子态重构以及滤波问题，在保证重构出的密度矩阵满足量子态约束条件下，将最接近雅可比交替方向乘子算法(proximaljacobianadmm，pj-admm)运用于基于压缩感知的高量子位状态的重构中，将问题转化为三个子问题，在重构出量子状态的同时，估计出稀疏干扰和高斯噪声，并且算法可以更快地找到更精确的解。另一方面，在每个子问题中添加近邻项以获得闭式解，避免大规模矩阵运算，极大降低了运算复杂度。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域的普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他附图。

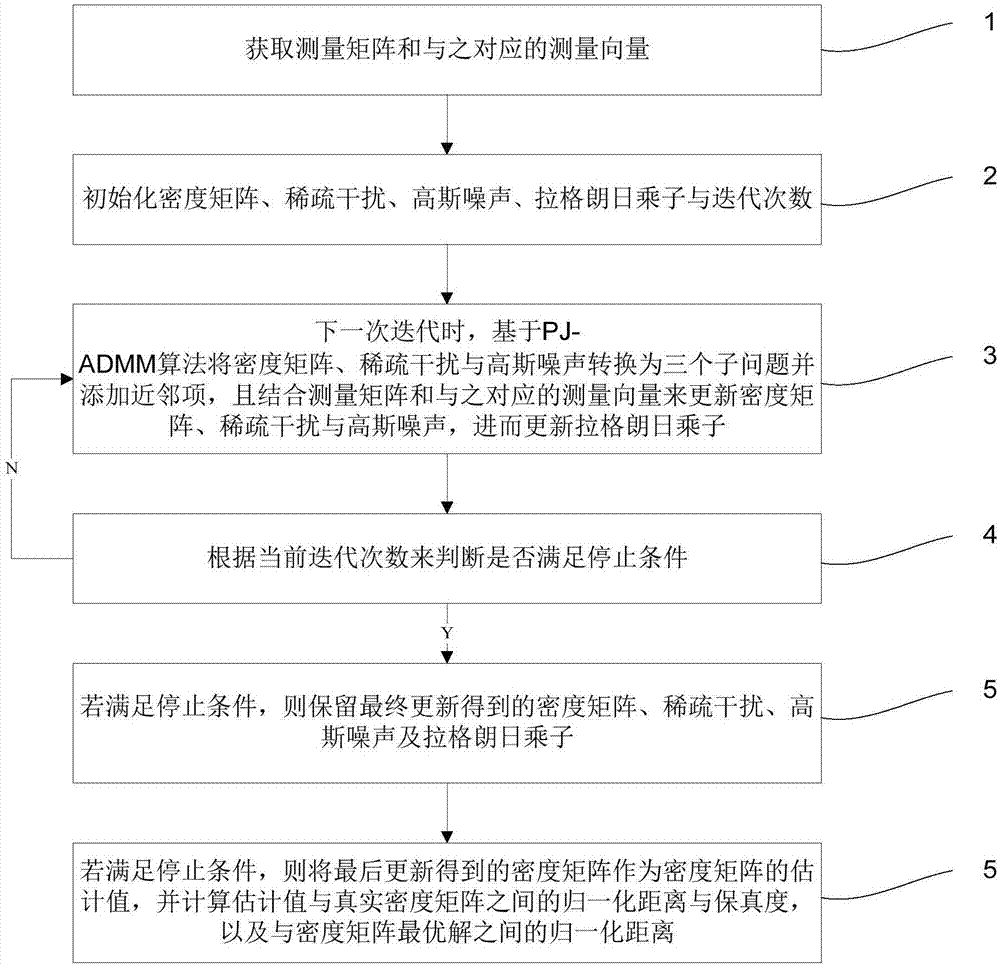
图1为本发明实施例提供的一种量子状态滤波方法的流程图；

图2为本发明实施例提供的迭代次数为1000时，本发明的pj-admm算法与admm和迭代收缩阈值(iterativeshrinkage-thresholding,ist)-admm算法重构量子态密度矩阵在不同采样率η下估计精度的对比结果；

图3为本发明实施例提供的采样率为0.4时，本发明的pj-admm与admm和ist-admm算法收敛性的对比结果；

图4为本发明实施例提供采样率为0.4时，本发明的pj-admm与admm和ist-admm算法估计精度的对比结果；

图5为本发明实施例提供的一种量子状态滤波器的示意图；

图6为本发明实施例提供的一种量子状态滤波器的工作流程图。

具体实施方式

下面结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明的保护范围。

本发明实施例提供一种量子状态滤波方法，该方法是一种带有状态稀疏干扰和测量高斯噪声的基于压缩感知的量子状态滤波方法，能够精确地求解带有稀疏干扰和高斯噪声的量子态估计问题。基于压缩感知理论，可以通过求解一个优化问题，利用少量的测量重构出低秩的密度矩阵。近邻雅可比交替方向乘子法(proximaljacobianadmm)是一种求解具有可分结构优化问题的高效算法，该算法将量子态估计问题拆分成三个子问题，其中第一个是关于密度矩阵核范数并且带有量子态约束的优化问题；第二个是关于稀疏干扰矩阵的l1范数优化问题；第三个是关于高斯噪声的l2范数优化问题，这三个子问题都不具有闭式解。本发明的方案是一种改进admm方法，其核心思想是在每个子问题中添加近邻项以获得闭式解，避免大规模矩阵运算，极大降低了运算复杂度。本发明的方案采用可调步长更新拉格朗日乘子，从而加快算法的收敛速度。本发明的方案给出保证算法收敛的条件，为参数选择提供依据。本发明的方案计算复杂度是o(md²)，相比现有的admm算法和ist-admm算法，能够通过更少的测量次数和迭代次数精确重构出量子状态。

如图1所示，本发明实施例提供的一种量子状态滤波方法的流程图，其主要包括如下步骤：

步骤1、获取测量矩阵a和与之对应的测量向量b。

本发明实施例中，测量矩阵测量向量m为测量次数，d为待估计量子态维数：d＝2ⁿ，n为量子态位数；表示复数域，表示实数域。

步骤2、初始化密度矩阵ρ^k、稀疏干扰s^k、高斯噪声e^k、拉格朗日乘子y^k与迭代次数k。

本发明实施例中，密度矩阵稀疏矩阵高斯噪声拉格朗日乘子

步骤3、下一次迭代时，基于pj-admm算法将密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k转换为三个子问题并添加近邻项，且结合测量矩阵a和与之对应的测量向量b来更新密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k，进而更新拉格朗日乘子y^k。

本发明实施例中，pj-admm算法在每个子问题中添加近邻项以获得闭式解，降低了计算复杂度，主要如下：

1)在第k+1次迭代时，结合测量矩阵a和与之对应的测量向量b，加入近邻项，并结合量子态约束条件，获得第k+1次迭代时的密度矩阵ρ^k+1的特征值，从而得到第k+1次迭代时的密度矩阵ρ^k+1；该过程的较佳实时方式如下：

对于密度矩阵的子问题，加入近邻项其中，定义二次伪范数为：p1＝τ1i-αa^ha，并结合任意的真实密度矩阵ρ必须满足的约束条件：ρ＝ρ^h、ρ≥0和tr(ρ)＝1；其中，i为单位矩阵；h为求解矩阵的共轭转置符号；tr(·)为求迹运算；zi指中的任意变量，结合所加入的近邻项zi代表ρ-ρ^k。同理在后文针对稀疏干扰子问题、高斯噪声子问题时，结合相应的近邻项，zi相应的代表s-s^k、e-e^k。

计算近邻密度矩阵其中，τ1为与密度矩阵相关的近邻步长，α为大于0的惩罚参数。

对进行特征值分解，得到特征值{ai}，进而在的条件下求解从而得到第k+1次迭代时的密度矩阵ρ^k+1的特征值{xi}；其中，d为待估计量子态维数。在求解得到第k+1次迭代时的密度矩阵ρ^k+1的特征值{xi}过程中，拉格朗日函数定义为其中，为拉格朗日乘子；根据凸优化理论，若是最优拉格朗日乘子以{xi}为变量最小化l({xi},β)即可得到原始最优解xi＝max{ai-β,0}；对于最优β，有该式等价于依次令β＝ai，i＝1,2,…d，从而确定最优β所属区间；若已知β在区间[at+1,at]内，得到且最优β由解出，即最后代入xi＝max{ai-β,0}求解出{xi}。

利用下式计算第k+1次迭代时的密度矩阵ρ^k+1：

ρ^k+1＝vdiag{xi}v^h；

其中，diag{xi}表示特征值{xi}为对角矩阵；为一个酉矩阵，表示复数域。

2)在第k+1次迭代时，结合测量矩阵a和与之对应的测量向量b，并加入近邻项，得到第k+1次迭代时的稀疏矩阵s^k+1；该过程的较佳实时方式如下：

对稀疏干扰子问题，利用近邻项其中，p2＝τ2i-αa^ha，将稀疏干扰子问题转化为：

其中，s为任意的真实稀疏矩阵，τ2为与稀疏矩阵相关的步长，||.||f表示frobenius范数，α为大于0的惩罚参数，γ＞0为正则化参数；近邻稀疏矩阵

引入软阈值收缩算符计算第k+1次迭代时的稀疏矩阵s^k+1：

其中，对于变量s，sign为正负1以及sign(0)＝0的符号函数。

3)在第k+1次迭代时，结合测量矩阵a和与之对应的测量向量b，并加入近邻项，得到第k+1次迭代时的高斯噪声e^k+1；该过程的较佳实时方式如下：

对于高斯噪声子问题，加入近邻项其中，p3＝τ3i，该问题具有闭式解，根据最优条件，第k+1次迭代时的高斯噪声的估计值e^k+1直接等于近邻高斯噪声

其中，e为任意的真实高斯噪声，τ3为与高斯噪声相关的近邻步长，θ＞0为正则化参数，α为大于0的惩罚参数。

4)结合第k+1次迭代更新的密度矩阵ρ^k+1、稀疏矩阵s^k+1与高斯噪声e^k+1计算第k+1次迭代时的拉格朗日乘子y^k+1，其公式如下：

y^k+1＝y^k-κα(a(ρ^k+1+s^k+1)+e^k+1-b)；

其中，κ＞0为调节拉格朗日乘子更新步长的参数；

本发明实施例中，调节拉格朗日乘子更新步长的参数κ，与密度矩阵相关的近邻步长τ1、稀疏矩阵相关的近邻步长τ2以及高斯噪声相关的近邻步长τ3满足如下关系：

且

步骤4、根据当前迭代次数来判断是否满足停止条件。

如果当前迭代次数大于设定的最大迭代次数，则判定满足停止条件，可以转入步骤5；否则，返回步骤3继续进行迭代。

示例性的，最大迭代次数可以为1000。

步骤5、若满足停止条件，则保留最终更新得到的密度矩阵、稀疏干扰、高斯噪声及拉格朗日乘子。

至此，完成量子状态的重构。重构的量子状态也即更新后的密度矩阵，同时还获得更新后的稀疏干扰、高斯噪声与拉格朗日乘子，正是这四个数据才形成量子状态滤波器。

步骤6、将最后更新得到的密度矩阵作为密度矩阵的估计值并计算估计值与真实密度矩阵ρ之间的归一化距离与保真度，以及与密度矩阵最优解ρ^*之间的归一化距离。

本发明实施例中，归一化距离和保真度是用来评价滤波效果的性能指标。

计算估计值与真实密度矩阵ρ之间的归一化距离(也叫归一化密度矩阵估计误差error)的公式如下：

计算估计值与密度矩阵最优解ρ^*之间的归一化距离公式如下：

计算估计值与真实密度矩阵之间的保真度的公式如下：

其中，tr(·)为求迹运算，保真度fidelity取值范围在[0,1]，当两个状态完全相同时值为1。

为了说明本发明上述方案的优越性，还与传统的admm和迭代收缩阈值(iterativeshrinkage-thresholding,ist)-admm算法进行了对比。

图2是最大迭代次数为1000时，分别采用本发明的近邻雅可比admm(pj-admm)、以及传统的admm和ist-admm算法重构5个量子位状态的密度矩阵时，与真实密度矩阵ρ之间的归一化距离随不同采样率η变化的结果，其中横坐标为采样率η，取值区间为[0.2％，0.6％]；纵坐标为密度矩阵估计值与真实值ρ(系统真实密度矩阵)之间的归一化距离(也叫归一化密度矩阵估计误差error)，其中带有方块的线条、圆圈的线条和菱形线条分别表示采用pj-admm(κ＝0.1)、admm和ist-admm算法的实验结果。实验所采用的计算机为：inteli5-3210mcpu、2核、主频2.5ghz、内存16g。从图2所示的实验结果可以看出采用本发明方案最终的归一化密度矩阵估计误差远小于传统的算法。

图3是量子位n为5，系统采样率为0.4，分别采用pj-admm、admm和ist-admm算法时，密度矩阵估计值与最优解ρ^*之间的归一化距离随迭代次数变化的实验结果。从最右侧由上至下的区分五个线条：第一个对应admm算法(即带有圆圈的线条)，第二个ist-admm算法(即带有菱形的线条)，后面三个分别对应参数κ＝1.4，0.6，0.1时的近邻雅可比admm(pj-admm)算法。从图3所示的结果也可以看出，采用本发明方案最终的归一化密度矩阵估计误差远小于传统的算法。

图4是量子位n为5，系统采样率为0.4，分别采用pj-admm、admm和ist-admm算法时，密度矩阵估计值与真实值之间的归一化距离随迭代次数变化的实验结果。从最右侧由上至下的区分五个线条：第一个对应admm算法(即带有圆圈的线条)，第二个ist-admm算法(即带有菱形的线条)，后面三个分别对应参数κ＝1.4，0.6，0.1时的近邻雅可比admm(pj-admm)算法。从图4所示的结果可以进一步看出，采用本发明方案最终的归一化密度矩阵估计误差远小于传统的算法。

本发明实施例上述方案，主要具有如下有益效果：

第一，针对带有稀疏干扰和高斯噪声的量子态估计问题，在保证重构出的密度矩阵满足量子态约束条件下，将pj-admm算法运用于基于压缩感知的高量子位状态的重构中，算法可以更快地找到更精确的解。

第二，在每个子问题后加入近邻项以获得闭式解，避免大规模矩阵运算，使运算复杂度大大降低。

第三，采用可调步长更新拉格朗日乘子，加快了收敛速度，同时给出满足算法收敛性的条件，为参数选择提供依据。

本发明另一实施例还提供量子状态滤波器，该量子状态滤波器基于上述方法来实现，如图5所示，其主要包括：

测量矩阵与测量向量获取模块，用于获取测量矩阵a和与之对应的测量向量b；

初始化模块，用于初始化密度矩阵ρ^k、稀疏干扰s^k、高斯噪声e^k、拉格朗日乘子y^k与迭代次数k；

更新模块，用于下一次迭代时，基于pj-admm算法将密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k转换为三个子问题并添加近邻项，且结合测量矩阵a和与之对应的测量向量b来更新密度矩阵ρ^k、稀疏干扰s^k与高斯噪声e^k，进而更新拉格朗日乘子y^k；

判断模块，用于根据当前迭代次数来判断是否满足停止条件；

量子状态保留模块，用于在满足停止条件时，保留最终更新得到的密度矩阵、稀疏干扰、高斯噪声及拉格朗日乘子；

估计值确定与距离及保真度计算模块，用于在满足停止条件时，将最后更新得到的密度矩阵作为密度矩阵的估计值并计算估计值与真实密度矩阵ρ之间的归一化距离与保真度，以及与密度矩阵最优解ρ^*之间的归一化距离。

需要说明的是，上述量子状态滤波器中包含的各个模块所实现的功能的具体实现方式在前面的方法实施例中已经有详细描述，可以配合图6所示的工作流程图来进行理解，故在这里不再赘述。

所属领域的技术人员可以清楚地了解到，为描述的方便和简洁，仅以上述各功能模块的划分进行举例说明，实际应用中，可以根据需要而将上述功能分配由不同的功能模块完成，即将量子状态滤波器的内部结构划分成不同的功能模块，以完成以上描述的全部或者部分功能。

通过以上的实施方式的描述，本领域的技术人员可以清楚地了解到上述实施例可以通过软件实现，也可以借助软件加必要的通用硬件平台的方式来实现。基于这样的理解，上述实施例的技术方案可以以软件产品的形式体现出来，该软件产品可以存储在一个非易失性存储介质(可以是cd-rom，u盘，移动硬盘等)中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述的方法。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明披露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应该以权利要求书的保护范围为准。