超混沌隐藏吸引子产生电路及其构建方法与流程

本发明涉及一种含有隐藏吸引子的忆阻超混沌系统，在原有的Lü系统的第一方程添加磁控忆阻项、第二方程添加线性反馈项和外部激励项。实现了一种磁控忆阻类Lü系统超混沌隐藏吸引子产生电路。

背景技术：

1971年提出了一种新的二端电路元件-忆阻器，并且从理论上预测了忆阻电荷与磁通量关系的存在性。2008年，美国惠普公司的研究人员将忆阻元件首次电路实现。2009年希捷公司的研究人员再次发明了一种基于电子磁性的自旋忆阻系统。近年来，忆阻元件因其具有非线性和记忆性，在人工神经网络、保密通信、存储器、生物模拟的研究预示存在广阔的应用前景。忆阻的出现使得延续摩尔定律成为了可能，其记忆特性、纳米级尺寸、快速开关以及耗电量低等特点为其各种应用的研究打下了坚实的基础。并且,随着材料、电子、系统、自动化等学科的发展,忆阻的研究和应用将会成为越来越热门的研究方向。

基于忆阻的非线性，越来越多的学者开始将其应用到混沌电路的产生中，从而在保密通信中有着许多应用。虽然惠普公司和希捷公司相继发明了忆阻元件的电路实现方法，但是其高昂的造价和较大的技术实现难度使得忆阻还无法达到商业化生产的水平。这使得许多研究人员还无法直接获得相关的忆阻器件进行各种科学研究，因此，利用电阻、电容、电感、运算放大器、模拟乘法器等分立元器件实现了多种忆阻模拟器，或者基于特殊拓扑形式的电路构建了若干广义忆阻模拟器，为忆阻及其应用电路的建模分析和实验观察做出了重要贡献。本文提出了一种磁控忆阻类Lü系统超混沌隐藏吸引子产生电路，进一步地拓展了忆阻模拟器的实现形式。并且，本申请提出在四维条件下获得的忆阻超混沌电路，没有平衡点，且能够产生超混沌隐藏吸引子，使得该系统具有更为复杂的动力学特性，预期该忆阻系统在保密通信密钥产生等方面的具有潜在的应用价值。新系统所生成的新颖且奇异的隐藏吸引子，不同于传统的自激吸引子，因为新系统不存在平衡点，其吸引盆与任何不稳定平衡点不相交，它是近年来新发现且新定义的一类吸引子，得到了学术界的广泛关注并取得了大量研究成果。因此，研究新忆阻系统的实现方法及其存在的隐藏吸引子有着重要的物理意义。

技术实现要素：

本发明所要解决的技术问题是构建一种用于磁控忆阻类Lü系统的超混沌隐藏吸引子产生电路及其构建方法。

为了解决上述技术问题，本发明提供了一种超混沌隐藏吸引子产生电路，包括：振荡系统和磁控忆阻对应的等效实现电路；其中所述振荡系统适于通过与等效实现电路相连以呈现相应隐藏振荡现象。

进一步，所述磁控忆阻等效实现电路包括：积分器，乘法器M_a、乘法器M_b，加法运算电路；其中所述磁控忆阻等效实现电路的输入端对应的状态变量–v_y经过积分器的积分运算后输出状态变量v_w，且该状态变量v_w经过乘法器M_a后与状态变量–v_y通过乘法器M_b完成乘法运算后，再通过加法运算电路输出–gW(v_w)v_y。

进一步，所述加法运算电路包括：与等效实现电路的输入端相连的第一电阻R/gα，与第二乘法器输出端相连的第二电阻R/gβ，且第一、第二电阻的另一端相连后作为等效实现电路的输出端；其中设置相应控制参数α＝4和β＝0.18。

进一步，所述振荡系统包括：第一、第二和第三积分通道；其中

第一积分通道内包括第一积分器，其有两个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/a后接到运算放大器U₁的反相输入端；

另一输入端适于接入状态变量–v_y，且串联另一电阻R/a后接于运算放大器U₁的反相输入端，该输入端还串联所述磁控忆阻器后接于运算放大器U₁的反相输入端，运算放大器U₁的反相输入端和输出端之间并联电容C₁，且运算放大器U₁的同相输入端接地；

所述运算放大器U₁的输出端适于输出状态变量v_x；以及

设置相应控制参数a＝36；

第二积分通道内包括第二积分器和一级反相器，其分别对应四个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/d后接于运算放大器U₂的反相输入端；

另一输入端适于接入状态变量v₁，且串联一电阻R/2后接于运算放大器U₂的反相输入端；

第三输入端适于接入状态变量–v_y，且串联一电阻R/b后接于运算放大器U₂的反相输入端；

第四输入端适于接入外部激励项–μ，且串联一电阻2R后接于运算放大器U₂的反相输入端，运算放大器U₂的反相输入端和输出端之间并联电容C₂，所述运算放大器U₂的输出端适于输出状态变量v_y；

运算放大器U₂的输出端和运算放大器U₃的反相输入端之间串联一阻值为36kΩ的电阻，运算放大器U₃的反相输入端和输出端之间并联另一阻值36kΩ的电阻，运算放大器U₂和运算放大器U₃的同相输入端均接地；

所述运算放大器U₃的输出端适于输出状态变量–v_y；以及

设置相应控制参数b＝20、d＝5、μ＝0.1和v₁＝v_xv_z；

第三积分通道内包括第三积分器，其分别对应两个输入端，即

一输入端适于接入状态变量v₂，且串联另一电阻R/2后接于运算放大器U₄的反相输入端；

另一输入端适于接入状态变量v_z，且串联一电阻R/c后接于运算放大器U₄的反相输入端，运算放大器U₄的反相输入端和输出端之间并联电容C₃，运算放大器U₄的同相输入端接地；

所述运算放大器U₄的输出端适于输出状态变量v_z；以及

设置控制参数c＝3和v₂＝–v_xv_y；并且

所述输入端v₁和v₂分别对应乘法器M₁和乘法器M₂的输出端，其中

乘法器M₁的两输入端分别对应输入端v_x和v_z；以及

乘法器M₂的两输入端分别对应输入端v_x和-v_y。

又一方面，本发明还提供了一种超混沌隐藏吸引子产生电路的构建方法，包括如下步骤

步骤S1，建立磁控忆阻对应的等效实现电路；

步骤S2，建立振荡系统；以及

步骤S3，将等效实现电路接入振荡系统内以呈现相应隐藏振荡现象。

进一步，所述磁控忆阻等效实现电路包括：积分器，乘法器M_a、乘法器M_b，加法运算电路；其中

所述磁控忆阻等效实现电路的输入端对应的状态变量–v_y经过积分器的积分运算后输出状态变量v_w，且该状态变量v_w经过乘法器M_a后与状态变量–v_y通过乘法器M_b完成乘法运算后，再通过加法运算电路输出–gW(v_w)v_y。

进一步，所述加法运算电路包括：与等效实现电路的输入端相连的第一电阻R/gα，与第二乘法器输出端相连的第二电阻R/gβ，且第一、第二电阻的另一端相连后作为等效实现电路的输出端；其中

设置相应控制参数α＝4和β＝0.18。

进一步，所述振荡系统包括：第一、第二和第三积分通道；其中

第一积分通道内包括第一积分器，其有两个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/a后接到运算放大器U₁的反相输入端；

另一输入端适于接入状态变量–v_y，且串联另一电阻R/a后接于运算放大器U₁的反相输入端，该输入端还串联所述磁控忆阻器后接于运算放大器U₁的反相输入端，运算放大器U₁的反相输入端和输出端之间并联电容C₁，且运算放大器U₁的同相输入端接地；

此时所述运算放大器U₁的输出端适于输出状态变量v_x；以及

设置相应控制参数a＝36；

第二积分通道内包括第二积分器和一级反相器，其分别对应四个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/d后接于运算放大器U₂的反相输入端；

另一输入端适于接入状态变量v₁，且串联一电阻R/2后接于运算放大器U₂的反相输入端；

第三输入端适于接入状态变量–v_y，且串联一电阻R/b后接于运算放大器U₂的反相输入端；

第四输入端适于接入外部激励项–μ，且串联一电阻2R后接于运算放大器U₂的反相输入端，运算放大器U₂的反相输入端和输出端之间并联电容C₂，所述运算放大器U₂的输出端适于输出状态变量v_y；

运算放大器U₂的输出端和运算放大器U₃的反相输入端之间串联一阻值为36kΩ的电阻，运算放大器U₃的反相输入端和输出端之间并联另一阻值36kΩ的电阻，运算放大器U₂和运算放大器U₃的同相输入端均接地；

所述运算放大器U₃的输出端适于输出状态变量–v_y；以及

设置相应控制参数b＝20、d＝5、μ＝0.1和v₁＝v_xv_z；

第三积分通道内包括第三积分器，其分别对应两个输入端，即

一输入端适于接入状态变量v₂，且串联另一电阻R/2后接于运算放大器U₄的反相输入端；

另一输入端适于接入状态变量v_z，且串联一电阻R/c后接于运算放大器U₄的反相输入端，运算放大器U₄的反相输入端和输出端之间并联电容C₃，运算放大器U₄的同相输入端接地；

所述运算放大器U₄的输出端适于输出状态变量v_z；以及

设置相应控制参数c＝3和v₂＝–v_xv_y；并且

所述输入端v₁和v₂分别对应乘法器M₁和乘法器M₂的输出端，其中

乘法器M₁的两输入端分别对应输入端v_x和v_z；以及

乘法器M₂的两输入端分别对应输入端v_x和-v_y。

本发明的有益效果是，本发明涉及磁控忆阻类Lü系统超混沌隐藏吸引子产生电路及其构建方法，其在原有的Lü系统的第一方程中添加磁控忆阻项，即第一积分通道；第二方程中添加线性反馈项和外部激励项，即第二积分通道、第三方程保持不变，实现了一种超混沌隐藏吸引子产生电路，并且该电路系统具有结构简单、易于理论分析和电路集成，可呈现出点吸引子、周期极限环、准周期极限环、混沌吸引子和超混沌吸引子等隐藏振荡现象，有较好的工程应用价值。

附图说明

下面结合附图和实施例对本发明进一步说明。

图1(a)磁控忆阻对应的等效实现电路的电路图；图1(b)振荡系统的电路图；

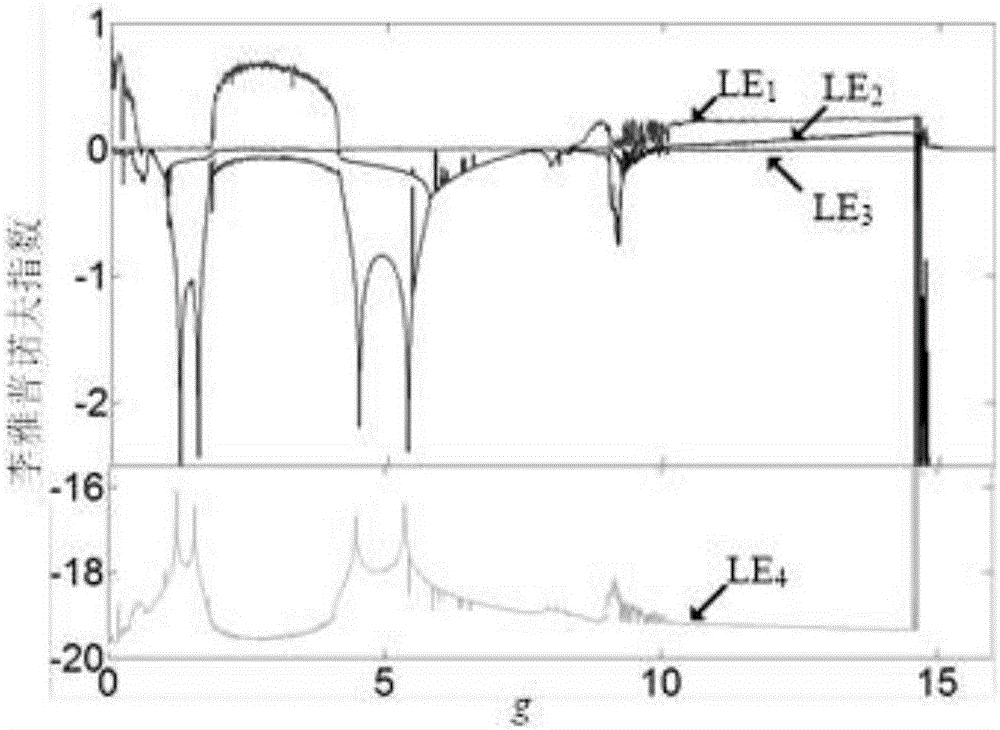
图2磁控忆阻类Lü系统超混沌隐藏吸引子产生电路模型数值仿真得到的随忆阻变化的李雅普诺夫指数图，说明该电路存在复杂的动力学特性；

图3磁控忆阻类Lü系统超混沌隐藏吸引子产生电路数值仿真得到的隐藏吸引子在x–z平面上的相轨图，其中图3(a)点吸引子；图3(b)周期2极限环轨道；图3(c)周期3极限环轨道；图3(d)准周期极限环轨道；图3(e)混沌轨道；图3(f)超混沌轨道；

图4磁控忆阻类Lü系统超混沌隐藏吸引子产生电路数值仿真得到的超混沌隐藏吸引子在4个相平面上的相轨图，其中图4(a)在x–z平面上；图4(b)在x–y平面上；图4(c)在x–w平面上；图4(d)在w–z平面上；

图5磁控忆阻类Lü系统超混沌隐藏吸引子产生电路实验测量捕捉的隐藏吸引子在x–z平面上的相轨图，其中图5(a)点吸引子；图5(b)周期2极限环轨道；图5(c)周期3极限环轨道；图5(d)准周期极限环轨道；图5(e)混沌轨道；图5(f)超混沌轨道；

图6磁控忆阻类Lü系统超混沌隐藏吸引子产生电路实验测量捕捉的超混沌隐藏吸引子在4个相平面上的相轨图，其中图6(a)在x–z平面上；图6(b)在x–y平面上；图6(c)在x–w平面上；图6(d)在w–z平面上。

具体实施方式

现在结合附图对本发明作进一步详细的说明。这些附图均为简化的示意图，仅以示意方式说明本发明的基本结构，因此其仅显示与本发明有关的构成。

实施例1

如图1(a)和图1(b)，本实施例1提供了一种超混沌隐藏吸引子产生电路，包括：振荡系统和磁控忆阻对应的等效实现电路；其中所述振荡系统适于通过与等效实现电路相连以呈现相应隐藏振荡现象。

进一步，所述磁控忆阻等效实现电路包括：积分器，乘法器M_a、乘法器M_b，加法运算电路；其中所述磁控忆阻等效实现电路的输入端对应的状态变量–v_y经过积分器运算后输出状态变量v_w，且该状态变量v_w经过乘法器M_a后与状态变量–v_y通过乘法器M_b完成乘法运算后，再通过加法运算电路输出–gW(v_w)v_y。

进一步，所述加法运算电路包括：与等效实现电路的输入端相连的第一电阻R/gα，与第二乘法器输出端相连的第二电阻R/gβ，且第一、第二电阻的另一端相连后作为等效实现电路的输出端；其中设置相应控制参数α＝4和β＝0.18。

具体的，所述等效实现电路的连接方式为：其输入端适于接入状态变量–v_y，且串联电阻R/2后接运算放大器U_a的反相输入端，运算放大器U_a的反相输入端和输出端之间并联电容C_a，此时运算放大器U_a的输出端适于输出状态变量v_w；乘法器M_a的两个输入端都适于接入状态变量v_w，乘法器M_a的输出端接乘法器M_b的一个输入端；M_b的另一个输入端适于接入状态变量–v_y，乘法器M_b的输出端与所述等效实现电路输出端之间串联电阻R/gβ，状态变量–v_y与等效实现电路输入端之间串联电阻R/gα，此时忆阻输出端输出-gW(v_w)v_x；运算放大器U_a的同相输入端接地；其中设置相应控制参数α＝4和β＝0.18。

所述磁控忆阻类Lü系统超混沌隐藏吸引子产生电路主电路如图1所示，其中x，y，z和w为系统的四个状态变量，v_x，v_y，v_z和v_w为系统对应电路的四个状态变量并有如下关系，其中根据仿真结果考虑所用运放和乘法器的电压范围，对电压状态变量进行了一定的缩放

x＝2v_x/V,y＝2v_y/V,z＝2v_z/V,w＝v_w/V。

进一步，所述振荡系统包括：第一、第二和第三积分通道；其中第一积分通道内包括第一积分器，其有两个输入端，即一输入端适于接入状态变量v_x，且串联一电阻R/a后接到运算放大器U₁的反相输入端；另一输入端适于接入状态变量–v_y，且串联另一电阻R/a后接于运算放大器U₁的反相输入端，该输入端还串联所述磁控忆阻器后接于运算放大器U₁的反相输入端，运算放大器U₁的反相输入端和输出端之间并联电容C₁，且运算放大器U₁的同相输入端接地；所述运算放大器U₁的输出端适于输出状态变量v_x；以及设置相应控制参数a＝36；第二积分通道内包括第二积分器和一级反相器，其分别对应四个输入端，即一输入端适于接入状态变量v_x，且串联一电阻R/d后接于运算放大器U₂的反相输入端；另一输入端适于接入状态变量v₁，且串联一电阻R/2后接于运算放大器U₂的反相输入端；第三输入端适于接入状态变量–v_y，且串联一电阻R/b后接于运算放大器U₂的反相输入端；第四输入端适于接入外部激励项–μ，且串联一电阻2R后接于运算放大器U₂的反相输入端，运算放大器U₂的反相输入端和输出端之间并联电容C₂，所述运算放大器U₂的输出端适于输出状态变量v_y；运算放大器U₂的输出端和运算放大器U₃的反相输入端之间串联一阻值为36kΩ的电阻，运算放大器U₃的反相输入端和输出端之间并联另一阻值36kΩ的电阻，运算放大器U₂和运算放大器U₃的同相输入端均接地；所述运算放大器U₃的输出端适于输出状态变量–v_y；以及设置相应控制参数b＝20、d＝5、μ＝0.1和v₁＝v_xv_z；第三积分通道内包括第三积分器，其分别对应两个输入端，即一输入端适于接入状态变量v₂，且串联另一电阻R/2后接于运算放大器U₄的反相输入端；另一输入端适于接入状态变量v_z，且串联一电阻R/c后接于运算放大器U₄的反相输入端，运算放大器U₄的反相输入端和输出端之间并联电容C₃，运算放大器U₄的同相输入端接地；所述运算放大器U₄的输出端适于输出状态变量v_z；以及设置控制参数c＝3和v₂＝–v_xv_y；并且所述输入端v₁和v₂分别对应乘法器M₁和乘法器M₂的输出端，其中乘法器M₁的两输入端分别对应输入端v_x和v_z；以及乘法器M₂的两输入端分别对应输入端v_x和-v_y。

三个积分通道与等效实现电路中通道所有相同标注的节点依次相连为一个四维振荡系统。与振荡系统中各积分电路各相同端口依次相连后，随忆阻增益变化，可实现输出周期极限环、准周期极限环、混沌吸引子和超混沌吸引子等隐藏振荡现象。

实施例2

在实施例1基础上，本实施例2还提供了一种超混沌隐藏吸引子产生电路的构建方法，包括如下步骤

步骤S1，建立磁控忆阻对应的等效实现电路；

步骤S2，建立振荡系统；以及

步骤S3，将等效实现电路接入振荡系统内以呈现相应隐藏振荡现象。

进一步，所述磁控忆阻等效实现电路包括：积分器，乘法器M_a、乘法器M_b，加法运算电路；其中

所述磁控忆阻等效实现电路的输入端对应的状态变量–v_y经过积分器的积分运算后输出状态变量v_w，且该状态变量v_w经过乘法器M_a后与状态变量–v_y通过乘法器M_b完成乘法运算后，再通过加法运算电路输出–gW(v_w)v_y。

进一步，所述加法运算电路包括：与等效实现电路的输入端相连的第一电阻R/gα，与第二乘法器输出端相连的第二电阻R/gβ，且第一、第二电阻的另一端相连后作为等效实现电路的输出端；其中

设置相应控制参数α＝4和β＝0.18。

进一步，所述振荡系统包括：第一、第二和第三积分通道；其中

第一积分通道内包括第一积分器，其有两个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/a后接到运算放大器U₁的反相输入端；

另一输入端适于接入状态变量–v_y，且串联另一电阻R/a后接于运算放大器U₁的反相输入端，该输入端还串联所述磁控忆阻器后接于运算放大器U₁的反相输入端，运算放大器U₁的反相输入端和输出端之间并联电容C₁，且运算放大器U₁的同相输入端接地；

此时所述运算放大器U₁的输出端适于输出状态变量v_x；以及

设置相应控制参数a＝36；

第二积分通道内包括第二积分器和一级反相器，其分别对应四个输入端，即

一输入端适于接入状态变量v_x，且串联一电阻R/d后接于运算放大器U₂的反相输入端；

另一输入端适于接入状态变量v₁，且串联一电阻R/2后接于运算放大器U₂的反相输入端；

第三输入端适于接入状态变量–v_y，且串联一电阻R/b后接于运算放大器U₂的反相输入端；

第四输入端适于接入外部激励项–μ，且串联一电阻2R后接于运算放大器U₂的反相输入端，运算放大器U₂的反相输入端和输出端之间并联电容C₂，所述运算放大器U₂的输出端适于输出状态变量v_y；

运算放大器U₂的输出端和运算放大器U₃的反相输入端之间串联一阻值为36kΩ的电阻，运算放大器U₃的反相输入端和输出端之间并联另一阻值36kΩ的电阻，运算放大器U₂和运算放大器U₃的同相输入端均接地；

所述运算放大器U₃的输出端适于输出状态变量–v_y；以及

设置相应控制参数b＝20、d＝5、μ＝0.1和v₁＝v_xv_z；

第三积分通道内包括第三积分器，其分别对应两个输入端，即

一输入端适于接入状态变量v₂，且串联另一电阻R/2后接于运算放大器U₄的反相输入端；

另一输入端适于接入状态变量v_z，且串联一电阻R/c后接于运算放大器U₄的反相输入端，运算放大器U₄的反相输入端和输出端之间并联电容C₃，运算放大器U₄的同相输入端接地；

所述运算放大器U₄的输出端适于输出状态变量v_z；以及

设置相应控制参数c＝3和v₂＝–v_xv_y；并且

所述输入端v₁和v₂分别对应乘法器M₁和乘法器M₂的输出端，其中

乘法器M₁的两输入端分别对应输入端v_x和v_z；以及

乘法器M₂的两输入端分别对应输入端v_x和-v_y。

对实施例1和实施例2的具体实现原理进行展开说明如下：

数学建模：本发明基于磁控忆阻类Lü系统的数学模型

在式(1)中，x、y、z为3个状态变量，a、b和c为3个控制参数。在式(1)基础上，第一方程添加磁控忆阻项、第二方程添加线性反馈项和外部激励项后，可建立磁控忆阻类Lü系统超混沌隐藏吸引子产生电路的无量纲方程为：

式(2)式有a、b、c、d和μ五个系统控制参数以及α和β两个忆阻内部参数。在下面的分析中，设置a＝36、b＝20、c＝3、d＝5、μ＝0.1、α＝4和β＝0.18，选择忆阻增益g为磁控忆阻系统的唯一控制参数。因外部激励项μ的存在，式(2)描述的忆阻系统不存在平衡点，因此该系统输出的相轨图均属于隐藏吸引子。

在式(2)中，w为磁控忆阻内部无量纲状态变量，且W(w)＝(α+βw²)。基于运算放大器和模拟乘法器的纯模拟电路可实现式(2)所描述的非线性动力学系统，其中，v_x、v_y、v_z、v_w分别代表4个积分电路通道的电容电压状态变量，其中根据(2)式数值仿真结果状态变量的变化范围太大，考虑到电路实现所用运放和乘法器的电压范围限制，对式(2)所描述的电压状态变量进行了一定的缩放：

x＝2v_x/V,y＝2v_y/V,z＝2v_z/V,w＝v_w/V (3)

RC为积分时间常数，且v₁＝v_xv_z和v₂＝–v_xv_y。因此，式(2)中的磁控忆阻类Lü系统超混沌隐藏吸引子产生电路原理图如图1所示，该电路状态方程表示如下：

其中，本文选用的磁控忆阻器的数学模型为：

式(5)中，α和β为2个正实常数，v_w为磁控忆阻的内部状态变量，v_y为忆阻的输入电压，i_y为忆阻的输出并用于第二积分通道中积分器的反向输入。一种基于运算放大器和模拟乘法器实现的非理想磁控忆阻W(v_w)的所述超混沌隐藏吸引子产生电路如图1(a)所示，其中积分时间常数RC与图1(b)的保持一致。至此，本发明构建了一种磁控忆阻类Lü系统超混沌隐藏吸引子产生电路的电路实现方案。

数值仿真如下：利用MATLAB仿真软件平台，可以对式(2)所描述的系统进行数值仿真分析。选择龙格-库塔(ODE45)算法对系统方程求解，可获得此忆阻系统状态变量的李雅普诺夫指数谱如图2所示和隐藏吸引子相轨图如图3、4所示。当磁控忆阻增益g＝16时，LE₁＝0、LE₂＝-2.982、LE₃＝-7.948、LE₄＝-8.077，由图3(a)可见，磁控忆阻系统呈现点隐藏吸引子；当磁控忆阻增益g＝1.7时，LE₁＝0、LE₂＝-0.06891、LE₃＝-0.594、LE₄＝-18.29，由图3(b)可见，磁控忆阻系统呈现周期二隐藏极限环；当磁控忆阻增益g＝5.96时，LE₁＝0、LE₂＝-0.2976、LE₃＝-0.299、LE₄＝-18.37，由图3(c)可见，磁控忆阻系统呈现周期三隐藏极限环。当磁控忆阻增益g＝7.95时，LE₁＝0、LE₂＝0、LE₃＝-0.1347、LE₄＝-18.83，由图3(d)可见，磁控忆阻系统呈现准周期隐藏极限环。当磁控忆阻增益g＝2.55时，LE₁＝0.6534、LE₂＝0、LE₃＝-0.06931、LE₄＝-19.53，由图3(e)可见，磁控忆阻系统呈现隐藏混沌吸引子。当磁控忆阻增益g＝13.4时，LE₁＝0.2411、LE₂＝0.1129、LE₃＝0、LE₄＝-19.32，由图3(f)可见，磁控忆阻系统呈现隐藏超混沌吸引子。磁控忆阻系统的隐藏超混沌吸引子，对应的不同平面的MATLAB数值仿真相轨图分别如图4(a)(b)(c)(d)所示。毫无疑问在四维维度下的超混沌系统大大地提高了忆阻电路动力学特性的复杂性，对于忆阻系统在保密通信等方面的具有潜在的应用价值。由此表明，该电路可以通过调节电路忆阻增益参数值g产生不同的混沌信号，得到多种具有复杂动力学特性的混沌行为，实现了一种可行的新型忆阻超混沌隐藏吸引子信号发生器。

实验验证：本设计分立元件选用金属膜电阻、精密可调电阻和独石电容，分立器件选用供电电压为±15V的OP07CP运算放大器和AD633JNZ模拟乘法器。实验过程中，由Agilent Technologies DSO7054B数字存储示波器完成实验波形捕捉。其中，参考电阻和参考电容分别选择为：R＝36kΩ、C＝100nF。此外，电阻R_e和R_f是联动可调的，其参数值分别为：R_e＝R/gα、R_e＝R/gβ。当增益g变化时，联动可调电阻的参数值分别固定为：R_e和R_f。忆阻系统(2)或是收敛到一个点的，或是周期的，或是准周期的，或是混沌的，或是超混沌的隐藏吸引子。随着增益g变化的点、周期、准周期、混沌和超混沌隐藏吸引子在xz相平面上的投影如图5所示。

对图4(a)(b)(c)(d)数值仿真中的超混沌隐藏吸引子相轨图进行了实验验证，实验结果分别如图6(a)(b)(c)(d)。

将图5和6实验测量结果与图3和4数值仿真结果作比较，可发现两者有着较好的一致性，由此验证了忆阻系统的复杂动力学行为的存在性。该结果进一步证实了该系统可呈现出稳定的点吸引子、周期极限环、准周期极限环、混沌吸引子和超混沌引子等隐藏振荡现象分析的正确性，电路实现一种磁控忆阻类Lü系统超混沌隐藏吸引子产生电路。

对比结果可以说明：实验电路中观测到的非线性现象与仿真结果具有较好的一致性，可以验证理论分析和数值仿真的正确性。因此，本发明所构建的一种磁控忆阻类Lü系统超混沌隐藏吸引子产生电路具有科学的理论依据和物理上的可实现性，可对混沌电路研究到相关领域工程应用起到积极的推动作用。

以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。