一种采用复杂曲面分层的3D混凝土打印路径规划方法与流程
一种采用复杂曲面分层的3d混凝土打印路径规划方法
技术领域
1.本发明涉及3d打印混凝土技术领域,更具体的说是涉及一种采用复杂曲面分层的3d混凝土打印路径规划方法。
背景技术:
2.3d打印混凝土实现几何成形的主要原理便是让打印头在打印过程中沿着特定的打印路径运动,与此同时,泵送系统通过管道将混合好的混凝土打印材料运输到打印头上,由打印头对混凝土打印材料进行挤出。3d打印混凝土领域最早提出的打印路径规划方法是水平逐层打印法,在此类打印过程中,设计者通过等高线式的切片逻辑将计算机中的构件模型进行等距切片,将三维的模型转变为一层一层二维的打印路径。随后,3d打印混凝土领域又衍生出了沿着曲面进行打印的路径规划方法,通过让机械臂沿着一个曲面模板(如球体)的表面运动,使挤出的混凝土打印材料附着在曲面模板上,从而产生变化更加丰富的形态效果。
3.虽然3d打印混凝土已经展现了实现复杂混凝土形态的诸多可能,但一些变化不规律,尤其是构件顶部起伏较大的形态无法用一个规则的平面或者曲面来进行切片,因此采用逐层打印或者曲面打印的方法都无法实现对应构件的打印。而且不同于球体、椭圆等规则的曲面,复杂曲面的uv坐标在空间中的变化不具有规律性。同时,当一个模型的底面与顶面不相互平行时,针对该模型切片产生的打印路径必然会出现层高的变化,若不能有效地控制每一层打印路径的高度,使其维持在适宜打印的范围内,则容易造成材料堆积或者供料不足的情况。
4.因此,如何提供一种适用于构件顶部形态不规则,且能够实现复杂曲面与规律的空间平面(或曲面)之间的过渡,并能在3d打印过程中有效控制打印高度的采用复杂曲面分层的3d混凝土打印路径规划方法是本领域技术人员亟需解决的问题。
技术实现要素:
5.有鉴于此,本发明提供了一种采用复杂曲面分层的3d混凝土打印路径规划方法,适用于顶部形态不规则构件打印,能够实现复杂曲面与规律的空间平面(或曲面)之间的过渡,并能在3d打印过程中对打印高度进行有效控制。
6.为了实现上述目的,本发明采用如下技术方案:
7.一种采用复杂曲面分层的3d混凝土打印路径规划方法,包括:
8.生成混凝土构件的三维模型,判断三维模型是否满足预设曲面分层标准;
9.在满足预设曲面分层标准的条件下,提取三维模型的顶部边缘曲线,并将其转换为nurbs曲线;
10.将nurbs曲线转化为具有uv方向的nurbs曲面;
11.确定切片参考平面,并将nurbs曲面投影至切片参考平面上,形成数组具有相同的uv坐标构成逻辑、但空间形态不相同的空间曲面;
12.根据相邻两个切片参考平面在模型范围内的最大高度差和每层打印路径的目标高度,计算相邻两个切片参考平面间的打印层数;
13.对形成的数组空间曲面进行曲面渐变计算,在各个参考平面与顶部nurbs曲面间生成对应数量的切片曲面;
14.利用切片曲面对三维模型进行切片,生成渐变曲线打印路径。
15.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,还包括:
16.根据预设打印宽度对每条渐变曲线打印路径向三维模型内部进行一定距离的偏移。
17.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,偏移的距离为预设打印宽度的1/2。
18.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,还包括:
19.采用等距离断点的方法将每条渐变曲线切分为连续的定位点;
20.以定位点在渐变曲线中对应的法线方向作为z方向,u坐标方向作为x方向,生成每个定位点的三维直角坐标,作为机械臂在每个定位点上的初始坐标位置。
21.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,还包括:
22.根据打印环境和机械臂型号,对每个定位点上的初始坐标位置进行调整。
23.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,所述预设曲面分层标准为:
24.三维模型顶部边缘曲线不处于三维空间平面或规则曲面上,且三维模型底部曲线处于三维空间平面上。
25.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,相邻两个切片参考平面间的打印层数的计算公式为:
26.n=int((h
max-h
min
)/h
27.其中,n为后相邻两个切片参考平面间的打印层数;h
max
为相邻两个切片参考平面在模型范围内的最大高度;h
min
为相邻两个切片参考平面在模型范围内的最小高度;h为每一层打印路径的目标高度,取值范围为6mm-18mm。
28.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,根据三维模型的形态变化趋势确定各个切片参考平面。
29.进一步的,在上述一种采用复杂曲面分层的3d混凝土打印路径规划方法中,各层渐变曲线打印路径的层高为均衡变化的。
30.经由上述的技术方案可知,与现有技术相比,本发明公开提供了一种采用复杂曲面分层的3d混凝土打印路径规划方法,具有以下有益效果:
31.1、本发明借助计算机辅助设计软件和可视化编程语言,通过将复杂构件的顶边缘转化为nurbs曲面,以及将nurbs曲面重投影至其他参考平面的方式,解决了复杂构件的3d打印路径规划中,底部平面与顶部曲面之间的过渡问题。
32.2、本发明通过对复杂构件顶边缘极点标高数据的提取和计算,结合曲面与平面间
渐变的方法,解决了复杂曲面切片过程中的高度控制问题,避免了因路径高度不适宜而产生材料堆积与供料不足的情况。实现了对顶部起伏变化明显的复杂混凝土形态的3d打印路径生成的目的。
33.3、本发明通过将机械臂定位点与其在曲面切片中对应的法线方向进行关联,解决了将复杂曲面切片转化为可定位坐标系的技术难点,实现了使机械臂贴合曲面切片法线方向进行移动的技术方法。
附图说明
34.为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据提供的附图获得其他的附图。
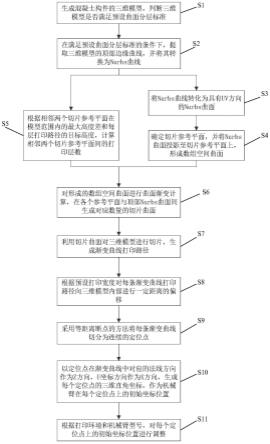
35.图1为本发明提供的采用复杂曲面分层的3d混凝土打印路径规划方法的流程图;
36.图2为本发明实施例一中,复杂曲面与一个参考平面的渐变分层示意图;
37.图3为本发明实施例二中的构件的结构示意图;
38.图4为本发明实施例二中复杂曲面与多个参考平面的渐变分层示意图。
具体实施方式
39.下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
40.如图1所示,本发明实施例公开了一种采用复杂曲面分层的3d混凝土打印路径规划方法,包括以下步骤:
41.s1、生成混凝土构件的三维模型,判断三维模型是否满足预设曲面分层标准;其中,混凝土构件的三维模型通过计算机辅助设计软件建立,且在建立之后,根据以下曲面分层标准标准判断该数字模型是否适用于本发明方法:(1)模型顶部边缘曲线不处于三维空间平面或者规则曲面上;(2)模型底部曲线处于三维空间平面上,若满足上述两个标准,则可以对三维模型信息进行进一步提取。
42.s2、在满足预设曲面分层标准的条件下,提取三维模型的顶部边缘曲线,并将其转换为nurbs曲线(非均匀有理b样条曲线)。
43.s3、将nurbs曲线转化为具有uv方向的nurbs曲面。
44.该步骤在可视化编程语言中,用s3获得的nurbs曲线生成具有uv方向的nurbs曲面,该步骤的目的在于通过nurbs曲面的uv坐标来描述和定位三维模型的顶部边缘曲线,这是空间平面和规则曲面都无法实现的。
45.s4、确定切片参考平面,并将nurbs曲面投影至切片参考平面上,形成数组具有相同的uv坐标构成逻辑、但空间形态不相同的空间曲面。
46.该步骤根据构件的几何形状,确定主要的切片参考平面,这些平面需要和三维模型的形态变化趋势相契合,并能将一个复杂的三维模型切分成多组简单的、易于切分的部
分,这是为了确保在曲面分层的步骤上生成的每个切片都能具备合理性,即不会产生无效或多余的切分。切片参考平面确定后,将nurbs曲面投影至这些参考平面上,组成数组具有相同的uv坐标构成逻辑、但空间形态并不相同的空间曲面。换言之,这些曲面在投影后呈现出来的是平面的形态,但仍然保持了原有曲面的uv特性,所以可以以uv特征作为桥梁,对平面上的曲面与模型顶部的复杂曲面进行渐变计算,实现平面与曲面之间的关联。
47.s5、根据相邻两个切片参考平面在模型范围内的最大高度差和每层打印路径的目标高度,计算相邻两个切片参考平面间的打印层数n。相邻两个切片参考平面间的打印层数n的计算公式为:
48.n=int((h
max-h
min
)/h
49.其中,n为切片后相邻两个切片参考平面间的打印层数;h
max
为相邻两个切片参考平面在模型范围内的最大高度;h
min
为相邻两个切片参考平面在模型范围内的最小高度;h为每一层打印路径的目标高度,取值范围为6mm-18mm,但根据实际打印构件的大小不同、以及不同打印设备所打印出的每层混凝度宽度不同,该取值范围会发生变化。
50.该步骤可利用基于rhino平台的可视化编程语言grasshopper对顶部边缘曲线中的最高点和最低点在三维模型中对应的净高度进行计算。
51.s6、对形成的数组空间曲面进行曲面渐变计算,在各个参考平面与顶部nurbs曲面间生成对应数量的切片曲面。
52.曲面渐变计算也可称作tween surface算法,是基于相邻两组空间曲面的uv特性,并通过可视化编程语言grasshopper中的pufferfish插件来实现的。由于s4中已经确保相邻两个切片参考平面间的空间曲面具有相同的uv特性,因此在三维空间中,可以将这两组空间曲面的各个uv网格的角点一一对应并相连,构成数组角点组。然后,在pufferfish插件中,通过输入对应的数列,便可在每组角点组之间生成等距的角点阵列(例如,若要在两组相邻切片参考平面中生成9组空间曲面,则可输入数列0,0.1,0.2,
……
,0.9,1,这表示在每两个对位角点的连线上,分别在其单位0,单位0.1,单位0.2,
……
单位0.9,单位1的位置上各确定1个空间点,其中单位0和单位1对应的点便是两个参考曲面上的uv网格点),通过这些角点生成的uv曲面便是所需生成的渐变曲面。
53.具体到本发明中,所需输入的数列与n相关,也就是说,要把一个模型中相邻两个切片参考平面间分成n层,就需要把区间[0,1]平均分成n段,生成数列0,1/n,2/n,
……
,(n-1)/n,1,然后将这组数列和对应的两个切片参考平面输入到tween curve算法中,便可在两个切片参考平面中生成(n-1)组渐变曲面,继而通过下面的步骤对模型进行切分。
[0054]
该步骤在可视化编程语言中,将s4中生成的空间曲面组合进行曲面渐变计算,以模型具有一个切片参考平面为例,以s5中计算出的打印层数n作为曲面渐变的目标数目,生成n个用以切分构件三维模型的切片曲面。得益于s5中的计算,这些切片之间的高度差将会满足3d打印每一层路径的高度要求,保证打印过程中不会因为上下层路径之间高度差过小而造成材料堆积,或高度差过大而造成供料不足。
[0055]
高度差即为生成渐变曲面后,每相邻的两个渐变曲面在模型范围内的最大高度与最小高度的差值。由于渐变曲面是通过上文描述的均分数列的方式生成,这个差值其实也约等于相邻两个切片参考平面之间的高差除以n。
[0056]
s7、利用切片曲面对三维模型进行切片,生成渐变曲线打印路径。该步骤借助布尔
运算,用s6中获得的切片曲面对三维模型进行切片,生成n个渐变曲线打印路径。
[0057]
通过上述s1-s7,可实现让3d打印过程中的每层混凝土打印材料都能顺畅地叠合,且每层渐变曲线打印路径的层高波动尽量小,或者均衡地变化,适用于顶部起伏变化较明显,无法用单一平面或规则曲面进行切片的3d打印混凝土构件。
[0058]
更有利的,在一个实施例中,还包括:
[0059]
s8、根据预设打印宽度对每条渐变曲线打印路径向三维模型内部进行一定距离的偏移。
[0060]
例如,根据3d打印混凝土构件所需的打印宽度b(根据构件大小、形态不同,适用的取值范围为30mm-60mm)对每条渐变曲线向形体内部进行偏移计算,偏移距离为b/2,偏移的参考面为每条曲线对应的切片曲面,这一步骤将在三维模型内部生成可用于定位机械臂坐标的参考曲线,以b/2为距离进行的偏移计算保证了3d打印的材料在挤出、流动、凝固后能够达到目标形态的实际边界。
[0061]
更有利的,还包括:
[0062]
s9、采用等距离断点的方法将每条渐变曲线切分为连续的定位点。
[0063]
该步骤的目的是为了保证机械臂在点与点之间移动时,其距离与速度能保持恒定。
[0064]
s10、以定位点在渐变曲线中对应的法线方向作为z方向,u坐标方向作为x方向,生成每个定位点的三维直角坐标,作为机械臂在每个定位点上的初始坐标位置。
[0065]
该步骤生成的每个直角坐标都是与对应的曲面切片相切的,也就是说,通过这个坐标来定位机械臂,将保证机械臂在运动的过程中始终贴合曲面切片的切线方向运动,这能使机械臂打印出来的肌理效果与三维模型的造型相互吻合。
[0066]
经过上述s1-s10后,还包括:
[0067]
s11、在可视化编程语言中,根据打印环境和机械臂型号的不同,对每个定位点上的初始坐标位置进行调整,使其满足机械臂运行的空间限制,然后结合机械臂的运行参数生成用以3d打印的g代码(g-code)。
[0068]
本发明经过上述步骤,通过不规则曲面与平面之间的渐变与分层,以及借助复杂渐变曲面生成机械臂定位坐标系的方法,拓展了3d打印混凝土技术可实现的形态类型,提高了复杂混凝土形态打印过程的精度与稳定性。
[0069]
下面结合具体实施例对本发明进行进一步说明。
[0070]
实施例一:复杂曲面与一个参考平面的渐变分层。
[0071]
如图2所示,该实施例是顶部由不规则曲线构成的混凝土花盆。其特点在于,除了顶部边缘为不规则曲线外,模型在平面上并无显著变化,模型构成较为简单,因此仅需要通过一个复杂曲面与一个参考平面进行渐变,即可实现路径生成。换言之,仅需将模型的底平面作为参考平面即可,其余步骤均可按照上述方法实施。在进行曲面层后,打印路径可以在花盆表面呈现出波浪形的纹理。这一实施例同样适用于其他平面变化较少,且无需额外支撑结构的三维模型。在图2中,1表示根据nurbs曲线生成nurbs曲面,2表示将nurbs曲面投影至三维模型的底平面,3表示生成渐变空间曲面,4表示切片后的几何形体。
[0072]
实施例二:复杂曲面与多个参考平面的渐变分层
[0073]
如图3所示,该实施例是顶部由不规则的曲面构成,且结构内部带有碗装结构、需
要额外支撑的混凝土雕塑,其中,图3
‑‑
1为该混凝土雕塑的整体造型,图3-2为该混凝土雕塑的剖面,内部包好碗状结构。因其构成较为复杂,所以需要多个参考平面对模型进行切分,使得每个参考平面能够与与模型造型的变化趋势相匹配。也就是说,除了模型的底平面外,还需要构建一个参考平面与碗装结构的底面相切,以及一个与雕塑顶部开口朝向比较近似的参考平面作为过渡,方能进行顶部曲面与平面之间的渐变分层。因此,在该实施例中,共包含了三个不同的参考平面,其余步骤均可按照上文描述的流程实施。这一实施例同样适用于其他平面变化丰富,或需额外支撑结构的三维模型。如图4所示,1表示根据nurbs曲线生成nurbs曲面,2表示确定几何形状的切片参考平面,3表示将nurbs曲面投影至三维模型的各个切片参考平面上,4表示生成渐变空间曲面,4表示切片后的几何形体。
[0074]
本说明书中各个实施例采用递进的方式描述,每个实施例重点说明的都是与其他实施例的不同之处,各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言,由于其与实施例公开的方法相对应,所以描述的比较简单,相关之处参见方法部分说明即可。
[0075]
对所公开的实施例的上述说明,使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的,本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下,在其它实施例中实现。因此,本发明将不会被限制于本文所示的这些实施例,而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1