考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法与流程

本发明涉及机器人稳定性领域，具体涉及一种考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法。

背景技术：

近年来，随着机器人技术日益成熟，在探险、焊接、太空、搬运、服务方面得到非常广泛的应用。多足机器人是一个复杂的机电一体化系统。作为被控对象，其本身是一个高度非线化、多变量、多参数耦合的复杂系统，使对其稳定性控制变的尤为困难。因此机器人稳定性控制问题成为近年来研究的热点问题。

机器人在野外行走，六足机器人相对二足、四足机器人而言，具有更丰富的运动步态。且六足机器人具有冗余的腿，机器人在复杂路面行走时，即使当一条腿或若干腿失效时，只要有三条腿能保持支撑状态，机器人能继续保持一定的运动能力。因此本发明以六足机器人在崎岖地面上行走作为研究对像。

目前针对六足机器人在崎岖地面上动态稳定性研究，通常采用是零力矩(ZMP)判定、压力中心法(COP)，然而其只考虑了机器人的足端反力，考虑因素过少，且不能反映机器人的抗干扰能力。传统的能量稳定边界法没有考虑到机器人的机械震荡属性。而李雅普诺夫稳定性理论难于对时变、非线性化做出瞬时响应。因此，目前需要一种机器人稳定性判定的方法能实时监测机器人的稳定性，使机器人能快速做出调整，保持稳定的行走。

技术实现要素：

针对现有的稳定性判定方法存在考虑影响因素太少或时效性差的问题，本发明提出一种考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法。该算法主要依据重心位置、虚拟弹性阻尼、合力矩得出，最终用于机器人在复杂路面行走时因外力冲击和自身惯性力矩作用，判定是否发生倾覆，以确保机器人稳定的行走。最终提出一种能适用于多种地形，且时效的稳定性计算方法。

本发明解决其技术问题所采用的技术方案是：

一种考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法，包括如下步骤：

步骤一：把机器人的翻转动作转换为包含弹簧阻尼特性的机械旋转系统，计算机器人的能量裕度表达式；

步骤二：建立机器人在笛卡尔坐标系下的D-H数学模型；

步骤三：结合步骤二解析机器人能量裕度函数所需有关参数。

进一步，所述的步骤一通过以下方式实现：

1.1)根据牛顿第二定律列出机器人的动力学微分方程：

其中，将绕边线翻转时的机器人，视为一个机械旋转系统，该系统由转动惯量为J_i、扭转刚度为K_S和粘性阻尼系数为C的阻尼器组成；

1.2)求解机器人绕边线旋转的实时重心处合力矩，即驱动力矩：

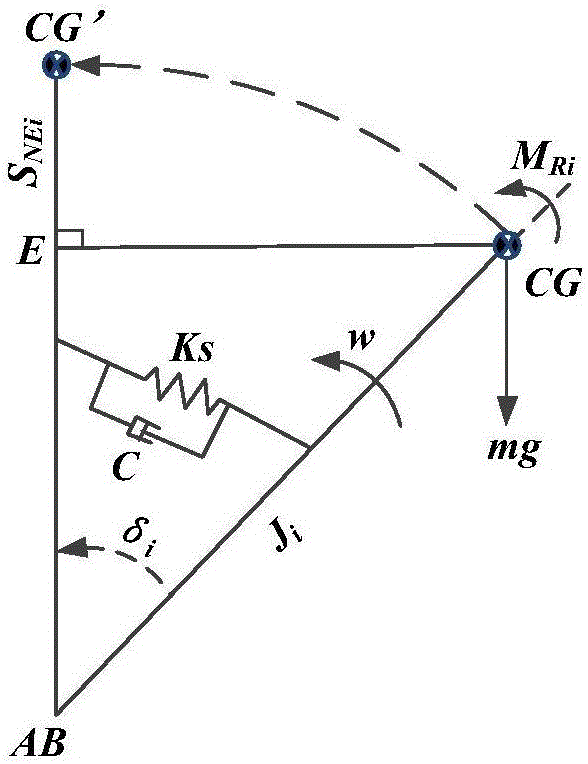
式中，M_Gi为实时重心处重力相对旋转边线产生的力矩；M_I为实时重心处的等效惯性力矩；M_ri为着地脚因支撑力产生的力矩；f_i为各足端竖直向上的力；θ_i为直线AB与水平面夹角，δ_i为重心绕边线旋转角度；θ为斜线倾角；r_i为各足端到旋转边线的距离；e_i为旋转边线的单位法向量，以支撑多边形逆时针方向为正方向；

1.3)系数K_S、C测定，根据上述的机械旋转系统整理得

两边进行拉氏变换，求得其传递函数为：

因此求得

式中，T_C、T_S分别为当机器人受到一个脉冲力时，机械旋转系统的震荡周期与稳定时间；

1.4)求解机器人考虑外力冲击干扰和阻尼的能量裕度

机器人绕边线旋转到最高点的势能变化：

机器人绕边线旋转到最高点的动能变化：

当w₀为正时：

当w₀为负时：

假设机器人绕边线旋转到最高点时w_i＝0，因此求得机器人当前位置因外界干扰不发生完全侧翻，所能抵抗的能量为：

E_i＝V_i-V₀+K_i-K₀

求得：

上述公式中，w₀、M_Ri'分别为实时重心位置绕边线旋转的角速度与合力矩，方向延旋转边线，以支撑多边形逆时针方向为正方向；

根据能量稳定裕量的概念可知，定义能量稳定裕度为SE_m，设最小稳定裕度SE，当SEm≥SE时，机器人能稳定工作。

再进一步，所述的步骤二通过以下方式实现：

在机器人的各关节处与躯体中心，建立笛卡尔坐标系，设坐标系C到坐标系O的之间的旋转变换为线性变换为^OP_C，因此求得C到O坐标系的齐次变换为：

当空间有n个坐标系时，若已知相邻坐标系之间的齐次变换矩阵，则：

M_0n＝M₀₁·M₀₂·…M_n-1n

其中M_ij为相邻坐标系的齐次变换，由此建立机器人各部分在坐标系O中的位置。

更进一步，所述的步骤三通过以下方式实现：

4.1)重心位置参数，

假设各部件均为匀质材料，因此其重心均在其几何中心处，根据步骤二中齐次变换矩阵，求各部件重心在世界坐标系的位置；

以躯体重心在世界坐标系中的位置求解为例：

式中，表示躯体重心在坐标系O_C中的位置；

同理求得各部件重心在O的位置，根据各重心位置坐标代入相关公式求得实时重心位置；

4.2)求解实时重心绕支撑边线旋转到最高位置的竖直位移；

设构成倾翻边线的两足端位置坐标：

A(x_A,y_A,z_A)，B(x_B,y_B,z_B)

首先，由几何关系式，求直线AB的表达式与重心CG到直线AB的距离H_i；

再次，求重心绕AB旋转到最高点的竖直位移；

S_NEi＝ECG'cosθ＝H_i(1-cosδ_i)cosθ_i

式中θ_i为直线AB与水平面夹角，δ_i为重心绕边线到最高点的旋转角度；

最后把解析出的相关参数代入到能量裕度函数中，求得机器人稳定裕度值，用于稳定性判定，保证机器人稳定工作。

本发明的有益效果主要表现在：

1、本发明考虑了机器人稳定行走的动态影响因素，包括角速度、力矩等。并在求解重心位置的能量裕度基础上，考虑机器人自身的弹簧阻尼特性，此方法能最大程度的计算出机器人能量稳定裕度。

2、考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法，能适用于多足机器人在复杂地形上行走时的动态稳定性分析，使机器人具有一定抵抗外力冲击的能力。

附图说明

图1是本发明的考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法，所应用的六足机器人结构示意图。

图2是六足机器人绕边线等效的机械旋转系统示意图。

图3是六足机器人在斜面行走示意图。

图4是六足机器人的单腿D-H模型。

图5是本发明的考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法的流程图。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图5，一种考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法，以六足机器人为例，包括机器人躯体和六条相互对独立的步行腿，所述计算方法包括以下步骤：

步骤一：把机器人的翻转动作转换为包含弹簧阻尼特性的机械旋转系统，计算机器人此时的能量裕度表达式；

1.1)根据牛顿第二定律可列出机器人的动力学微分方程：

其中，将绕边线翻转时的机器人，视为一个机械旋转系统，该系统由转动惯量为J_i、扭转刚度为K_S和粘性阻尼系数为C的阻尼器组成。

1.2)求解机器人绕边线旋转的实时重心处合力矩，即驱动力矩：

式中，M_Gi为实时重心处重力相对旋转边线产生的力矩；M_I为实时重心处的等效惯性力矩；M_ri为着地脚因支撑力产生的力矩；结合图3中所示，f_i为各足端竖直向上的力；θ_i为直线AB与水平面夹角，δ_i为重心绕边线旋转角度；θ为斜线倾角；r_i为各足端到旋转边线的距离；e_i为旋转边线的单位法向量，以支撑多边形逆时针方向为正方向。

1.3)系数K_S、C测定方法，根据上述的机械旋转系统整理得

两边进行拉氏变换，求得其传递函数为：

因此求得：

式中，T_C、T_S分别为当机器人受到一个脉冲力时，机械旋转系统的震荡周期与稳定时间。

1.4)求解机器人的考虑外力冲击干扰和阻尼的能量裕度

机器人绕边线旋转到最高点的动能变化：

当w₀为正时：

当w₀为负时：

假设机器人绕边线旋转到最高点时w_i＝0，因此机器人求得当前位置因外界干扰不发生完全侧翻，所能抵抗的能量为：

E_i＝V_i-V₀+K_i-K₀

求得：

上述公式中，w₀，M_Ri'分别为实时重心位置绕边线旋转的角速度与合力矩，方向延旋转边线，以支撑多边形逆时针方向为正方向；

根据能量稳定裕量的概念可知，定义能量稳定裕度为SE_m，其值越大，表示机器人越稳定。然而为了确保机器人在外力冲击作用下安全可靠的工作，设最小稳定裕度SE，当SEm≥SE时，机器人能稳定工作。

有益于机器人在行走过程中，根据实时检测的关节转角与机身角速度等有关变量，计算当前能量裕度值，判定机器人是否能稳定行走。并建立适当的自适应控制算法，根据环境情况和系统状态，优化关节驱动参数，保证机器人稳定工作。

步骤二：根据机器人的运动学，建立机器人在笛卡尔坐标系下的D-H数学模型。由于机器人的六条腿相互独立，且完全相同。因此根据机器人单腿的D-H数学模型可推导出整机的D-H模型。

如图4所示，首先分别在机器人单腿各关节处，以及机器人躯体中心，建立笛卡尔坐标系。再进行两个坐标之间的齐次变换，以躯体坐标到世界坐标系之间齐次变换为例：

上式为坐标系OC到ΣO旋转变换，其中α、β、γ分别表示机器人在世界坐标系O下的机身姿态,且cα＝cosα，sα＝sinα，cβ,sβ,cγ,sγ依次类推。上述公式中的角度，分别由陀螺仪、关节舵机直接反馈得出。

^OP_C表示坐标系O_C原点在O中相对位置。

上式为坐标系OC到O的平移变换

求得两坐标之间的齐次变换:

当空间有n个坐标系时，若已知相邻坐标系之间的齐次变换矩阵，则：

M_0n＝M₀₁·M₀₂·…M_n-1n

其中M_ij为相邻坐标系的齐次变换，因此求出机器人各部分在坐标系O中的位置；

步骤三：本发明的考虑外力冲击干扰和阻尼的多足机器人能量裕度计算方法，与机器人的实时重心相关，为了计算方便，假设各部件均为匀质材料，即重心均在其几何中心处，由此得出在其相应的笛卡尔坐标系中的位置，如图4所示；

3.1)通过步骤二中求出的齐次变换矩阵，得出各部件重心在世界坐标系位置。

式中，表示躯体重心在坐标系O_C中的位置

同理求得各部件重心在O的位置。代入以下公式求得机器人实时重心：

其中，W为机器人的总量，单位kg；n为机器人的足数，x_o,y_o,z_o为机身重心在坐标系O中位置，x_j,y_j,z_j为各部件重心在O中位置坐标

3.2)结合图4求解实时重心绕支撑边线翻转时到最高位置时的竖直位移S_NEi。

首先假设构成倾翻边界的两足端位置坐标：

A(x_A,y_A,z_A)，B(x_B,y_B,z_B)

求直线AB的表达式：

再次求重心CG到直线AB的距离为：

最后，通过直线与面的几何关系，求重心绕AB旋转到最高点的竖直位移：

S_NEi＝ECG'cosθ_i＝H_i(1-cosδ_i)cosθ_i

式中，H_i为实时重心到支撑边线的垂直距离；CG’为CG绕直线AB旋转所能达到的最高高度点，δ_i为重心绕边线的旋转角度；θ_i为直线AB与水平面的夹角。最后把解析出的相关参数代入到能量裕度函数中，求得机器人稳定裕度值，用于稳定性判定，保证机器人稳定工作。