一种对未知结构参数的光纤进行非简并模式功率分解方法与流程

本发明涉及应用光纤光学领域，尤其涉及一种对未知结构参数进行非简并模式功率分解方法。

背景技术：

在光纤技术中，光纤的本征模的功率权重的测量成为一个重要的课题，在许多应用中都有很高的要求，功率分解是通过控制单模运行的光纤激光器来提高光束质量的必要手段。在光纤通信中，采用模分复用技术可以大大提高光纤网络的容量。光纤中光场携带的信息可以用功率分解的方法进行解调。

近年来提出了许多功率分解的方法。当成像设备记录光纤场的强度分布时，可以使用数值方法(例如线搜索、单纯形搜索算法、gerchberg-saxton算法和spgd算法)来计算光纤中每种模式的振幅和相位系数。然而光强度图像易于记录，但光纤模场的相位信息易丢失。这些方法要么容易陷入局部最优，对初值敏感；要么分解效果差，收敛时间长。为了加快模式的功率分解过程，提出了光相关分析(oca)方法：通过引入计算机生成的全息图(cgh)，它包括与本征模振幅和相位相对应的透射率函数，可以在光衍射过程中实时完成模式的功率分解。虽然oca方法不需要复杂的数值计算。但是cgh的设计和制造是困难的，它只能适用于特定类型的光纤。然而，以上所讨论的所有方法都需要所用光纤的结构参数，应在功率分解过程之前获得特征模式，利用光纤的折射率分布可以计算出光纤的特征模。这限制了它们的应用。在不了解光纤折射率分布的情况下，可以使用光谱和空间(s²)成像技术直接分析光纤中的模态场。该方法通过光学光谱的空间相关的傅立叶变换，得到各模式的折射率和相对功率。经过nguyen等人的改进，s²成像技术变得更加高效。然而，在傅立叶变换中也可以识别出杂散模式，从而导致用复杂的步骤来消除杂散模式。对于高分辨率的测量，s²方法会大幅降低计算速度。

技术实现要素：

针对现有技术中存在的问题，受s²方法的启发，提出了一种新的光纤的模式功率分解的方法。通过主成分分析算法(pca)，从频率相关波前(即光纤中的复场分布)中提取光纤中的光场特征。通过分析得到一套完整的伪模式，光纤场作为这些伪模式的线性组合。基于酉变换的性质，在不知道光纤的结构参数的情况下分析光纤的本征性质。确定非简并模式的数目，以及每种非简并模式的有效折射率。与s²方法类似，本发明不需要事先了解光纤的结构参数。利用简单的优化算法，有效地计算出非简并模式(而非伪模式)的功率权重。该方法为分析光纤中的光场提供了另一种观点。作为一种通用的方法，它可以应用于各种光纤，如少模光纤和微结构光纤。

本发明采用的技术手段如下：

一种对于未知结构参数的光纤进行非简并模式功率分解的方法，包括步骤如下：

步骤1，将需要计算的光纤非简并模式的有效折射率的光纤嵌入数字全息系统中，通过改变光源频率获得多幅干涉图像，并重建成波前样本，通过主成分分析算法提取波前样本的共性特征，并用伪模式的线性组合表示光纤场的波前样本；

步骤2，以两频率对应波前的伪模式的模态系数之间的内积，行傅里叶变换，识别出真实光纤模式的有效折射率；

步骤3，采用梯度下降算法，建立功率权重、本征模的有效折射率和频率差之间的函数关系，进而获得光纤中非简并模式的功率权重。

进一步地，上述步骤1，利用主成分分析算法得到伪模式的波前样本，具体方法为：

s101：获得光纤场的波前样本；

光源为频率可调激光器，改变光源频率通过数字全息系统获得干涉图像，在m个光源频率下，即光源频率为f＝f⁽¹⁾,f⁽²⁾,…f^(k),…f^(m)的条件下：

将获得的干涉图像重建为波前样本，每个波前样本都是一个l×l大小的二维复矩阵，光源频率f^(k)时，对应的波前样本能够表示如下形式：

写成列向量尺寸为l²×1，并能够表示成如下形式：

ψ^(k)表示的是在光源频率为f^(k)条件下，获得的波前样本对应的一维列向量；

s102：将m幅对应不同光源频率的干涉图像按s101中的方法重新排列成m个一维列向量，分别表示为ψ⁽¹⁾,ψ⁽²⁾,…ψ^(m)，通过以下公式计算m个一维列向量的平均向量

通过如下公式计算数据矩阵φ：

s103：计算s102中所述数据矩阵的协方差矩阵并计算该协方差矩阵的特征值和协方差矩阵的特征向量；

s104：在所述协方差矩阵的特征值中有n个非零特征值，这些特征值与特征向量分别表示为；

特征值表示为λ＝[λ1,λ2,…λn]，对应的特征向量为v＝[v1,v2,…vn]；

s105：通过s104中求得的特征向量，定义伪模式波前样本为：

s106：根据主成分分析算法的原理，当光纤的本征模未知时，伪模式的波前样本用一组基函数表示：

伪模式的波前样本表示为：

其中，是伪模式的模态系数，

进一步地，上述步骤2，计算光纤场的非简并模式的有效折射率：

s201：根据光的波导理论，波前样本由本征模表示为：

其中，分别是本征模和伪模式的模态系数，分别是本征模和伪模式；

同步骤1：

本征模和伪模式的模态系数之间的关系表示为：

b^(k)＝a^(k)t；

其中，b^(k),a^(k)可表示为：

t为转换矩阵；

s202：本征模的模态系数表示为：

其中，an是振幅系数，是相位系数；

s203：定义频率为f^(k)和f⁽¹⁾的波前的模态系数内积为：

其中，

s204：令δf^(k)＝f^(k)-f⁽¹⁾，其中δf^(k)和的关系表示为

其中，c是光速，l是测量光纤的长度，neff，n是n阶本征模的有效折射率；

s205：模态系数内积x^(k)为关于δf^(k)的函数，即：

s206：对模态系数内积x^(k)进行傅里叶变换获得功率非零的光纤模式的有效折射率。

进一步地，上述步骤3，计算光纤场的功率权重，包括以下步骤：

s301：利用模态系数内积x^(k)，梯度下降算法对波前样本计算功率权重的系数；其中令：

其中，

pn是功率权重的系数，将频率差为δf的两个测量波前样本作为训练样本。

s302：对于梯度下降算法,定义的代价函数表示为：

分配pn＝1/n作为最初的初始值，然后，按照算法更新规则重复执行迭代计算；所述算法的更新规则为：

其中，

α是学习率，当pn的参数收敛到使代价函数j(p)最小化的值时，优化过程终止，此时pn的值就是所求的功率权重。

本发明具有以下优点：

1、本发明应用主成分分析算法，从光纤中的波前样本中提取光纤中的光场的共性特征，得到一套完整的伪模式，光纤的波前样本可以通过这些伪模式的线性组合表示，可以在不知道结构参数的情况下得到光纤的本征性质。同时由于主成分分析算法本身降维的特性，可以提高计算效率。

2、本发明对于未知结构参数的光纤，可以通过以伪模式表示的光纤的波前样本，确定非简并模式的数目和通过傅里叶变换得出每种模式的有效折射率，通过简单的优化算法，可以有效地计算出非简并模式(而非伪模式)的功率权重。

附图说明

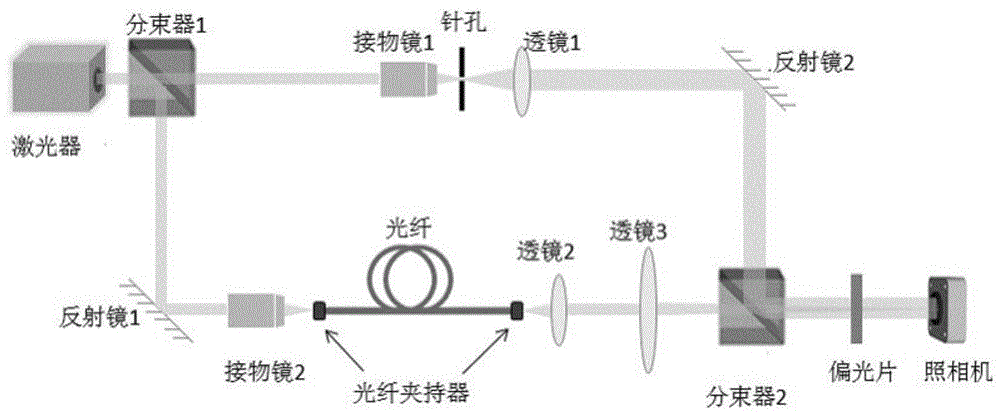
图1为数字全息系统记录被测光纤中的频率相关波前。bs1和bs2是分束器。l1、l2和l3是焦距透镜。

图2为当λ＝633nm时，smf-28光纤中支持的10个本征模的强度分布。(a)lp01，(b)lp02，(c)lp11e，(d)lp11o，(e)lp12e，(f)lp12o，(g)lp21e，(h)lp21o，(i)lp31e，(j)lp31o。

图3为(a)λ＝633nm的光纤模式的振幅系数，(b)λ＝633nm的光纤模式的相位系数，(c)波前样本的强度分布，(d)波前样本的相位分布。

图4为(a)通过主成分分析算法分析的伪模式的贡献率，从大到小排列，前六个贡献率的总和几乎达到100％，图(b)～图(g)分别为通过对应于(a)中的前六个主成分的分析获得的伪模式。

图5为(a)x^(k)在不同频率差下的内积，(b)x^(k)的傅立叶分析，以计算本征模的有效折射率。可以识别六个峰值(由点标记)，对应于六个非简并模式。

图6.理论值(左边色条)和测量值(右边色条)之间的模态功率权重的比较。

图7为本算法的算法流程图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例1

如图1所示，将长度为l的光纤嵌入在数字全息系统中，该系统的光源是频率可调激光器。利用分束器1将频率可调激光器的入射光分成两束。一个光束作为参考臂在自由空间中传播。另一束光以l的长度耦合到被测光纤中，在光纤的输出端，通过4f成像配置(透镜2和透镜3)将光纤中的光场成像到ccd相机的像面上。通过分析两光束之间的干涉图样，可以重建光纤场的波前样本。

在本例中，分析了标准smf-28通信光纤中的光场。光纤芯层直径为8.2μm，数值孔径为na＝0.14。当入射波长为633nm时，光纤的归一化频率为v＝k0ana＝5.698。通过求解本征方程，模拟光纤中有10种模式，由lp01，lp02，lp11e，lp11o，lp12e，lp12o，lp21e，lp21o，lp31e和lp31o表示，其中e和o在模式表示的下标中。用于区分相同的模式顺序的偶数和奇数模式。每对偶数和奇数模式彼此简并。因此，此光纤中支持6种非简并lp模式，这些模式的强度分布如图2所示。

波前样本可以通过图1所示的数字全息成像系统重建。在该模拟中，光纤的模态系数的幅度和相位的系数的选择如图3所示，当光源波长为633nm时。通过这些模式与特定模态系数的线性组合可以获得总场的波前样本。

当光源频率(或波长)发生变化时，模态系数的振幅系数不变，相位系数在通过长度为l的测量光纤后发生偏移变化。频移与相移之间的关系为：

在这项工作中，频移的步长是1.5ghz。波前样本在200个频率点处生成，并且频率范围的对应宽度是300ghz(即，波长范围是从633nm到632.6nm)。在此范围内，我们假设光纤模式的有效折射率是频率无关的。

通过数字全息系统，生成了200幅干涉图像，。

获取光纤伪模式的波前分布包括以下步骤：

s101：获得光纤场的波前样本；

光源为频率可调激光器，改变光源频率通过数字全息系统获得干涉图像，在m＝200个光源频率下，即光源频率为f＝f⁽¹⁾,f⁽²⁾,…f^(k),…f⁽²⁰⁰⁾的条件下，获取200幅干涉图像：

将获得的干涉图像重建为波前样本，每个波前样本都是一个l×l大小的二维复矩阵，光源频率f^(k)时，对应的波前样本能够表示如下形式：

写成列向量尺寸为l²×1，并能够表示成如下形式：

ψ^(k)表示的是在光源频率为f^(k)条件下，获得的波前样本对应的一维列向量；

s102：将m＝200幅对应不同光源频率的干涉图像按s101中的方法重新排列成200个一维列向量，分别表示为ψ⁽²⁾,ψ⁽²⁾,…ψ^(m)，通过以下公式计算m＝200个一维列向量的平均向量

通过如下公式计算数据矩阵φ：

s103：计算s102中所述数据矩阵的协方差矩阵并计算该协方差矩阵的特征值和协方差矩阵的特征向量；

s104：在所述协方差矩阵的特征值中有n个非零特征值，这些特征值与特征向量分别表示为；

特征值表示为λ＝[λ1,λ2,…λn]，对应的特征向量为v＝[v1,v2,…vn]；

s105：通过s104中求得的特征向量，定义伪模式波前样本为：

s106：根据主成分分析算法的原理，当光纤的本征模未知时，伪模式的波前样本用一组基函数表示：

伪模式的波前样本表示为：

其中，是伪模式的模态系数，

通过带入数据计算得知：

采用主成分分析算法对样本进行处理，得到伪模式。前10个主要成分(从大到小排列)的贡献率如图4(a)所示。前6个值占主导地位，其贡献率之和接近100％。并可以得到六种伪模式。因此，伪模式和非简并模式的数目是相等的。然而，在这种情况下，具有相同有效指数和不同场分布(如lp11o和lp11e)的简并模式是无法区分的。伪模式的强度和相位分布如图4所示：

进一步的，计算光纤场的非简并模式的有效折射率包括以下步骤：

s201：根据光的波导理论，波前样本由本征模表示为：

其中，分别是本征模和伪模式的模态系数，分别是本征模和伪模式；

同步骤1：

本征模和伪模式的模态系数之间的关系表示为：

b^(k)＝a^(k)t；

其中，b^(k),a^(k)可表示为：

t为转换矩阵；

s202：本征模的模态系数表示为：

其中，an是振幅系数，是相位系数；

s203：定义频率为f^(k)和f⁽¹⁾的波前的模态系数内积为：

其中，

s204：令δf^(k)＝f^(k)-f⁽¹⁾，其中δf^(k)和的关系表示为

其中，c是光速，l是测量光纤的长度，neff，n是n阶本征模的有效折射率；

s205：模态系数内积x^(k)为关于δf^(k)的函数，即：

s206：对模态系数内积x^(k)进行傅里叶变换获得功率非零的光纤模式的有效折射率。

通过带入数据计算得知：

模态系数内积x^(k)如图5(a)所示：模态系数内积x^(k)的傅里叶变换如图5(b)所示：有效折射率可由峰值位置确定，峰值位置用图5(b)中的点标记。与s²技术相比，模态系数内积x^(k)的傅里叶谱中没有杂散模式。因此，可以简化功率分解过程。

通过求解本征方程得到的理论有效指标值与采用该方法得到的实测值的最大偏差为1×10^-5。这种偏差可以通过进一步增加记录的频率点的数量来减小。

进一步的，计算光纤场的功率权重包括以下步骤：

s301：利用模态系数内积x^(k)，梯度下降算法对波前样本计算功率权重的系数；其中令：

其中，

pn是功率权重的系数，将频率差为δf的两个测量波前样本作为训练样本。

s302：对于梯度下降算法,定义的代价函数表示为：

分配pn＝1/n.作为最初的初始值，然后，按照算法更新规则重复执行迭代计算；所述算法的更新规则为：

其中，α是学习率，当pn的参数收敛到使代价函数j(p)最小化的值时，优化过程终止，此时pn的值就是所求的功率权重。

通过带入数据计算得知：

对于有效指标的测量，需要大量的波前样本来减小误差。为了确定功率权重，可以大大减少波前样本的数目。本实施例选取x^(k)的前15个内积作为样本集。功率权重由梯度下降算法求得，结果如图6所示：左边色条代表各模式的功率权重，右边色条代表所提出算法的实测值。从光纤场的波前样本可以很好地反演出功率权重。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围。