基于以高斯模型为实例整合重建的磁共振扩散成像方法与流程
本发明涉及磁共振成像技术领域,尤其涉及一种基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法。
背景技术:
磁共振扩散张量成像能够无创检测人体水分子的微观布朗运动,提供人体纤维连接的结构信息、以及组织的功能信息,是一种重要的神经影像技术,在临床与研究中都得到广泛的应用。目前,磁共振扩散张量成像是唯一能够无创检测人体神经纤维束的成像技术。
磁共振扩散成像的对比度机制可以采用高斯扩散模型,该高斯扩散模型中的扩散张量参数反映了组织的扩散性质。通过扩散张量,可以直接计算得到扩散系统、各向异性扩散参数等重要图像指标,例如,各向异性分数(fractionalanisotropy,英文简称fa)、平均扩散系数(meandiffusivity,英文简称md)、扩散张量特征方向。这些图像参数指标被应用于人体大脑、脊髓、骨骼肌组织连接的诊断。
相关技术中,传统的磁共振扩散张量成像通过施加不少于6个方向的扩散梯度编码,通过高斯扩散模型计算得到扩散张量。为了获得更准确的扩散张量,通常需要更多的扩散编码梯度方向,例如32个扩散编码方向,大大增加了信号采集时间。在分辨率方面,多次激发平面回波序列采集能够达到高于传统单次激发技术分辨率的扩散图像,但是多次激发采集也会导致更长的采集时间。因此,尽管高分辨率、多扩散梯度采集能够实现更准确的高质量扩散成像,但所需的图像扫描时间远长于目前临床使用的传统方法,限制了神经影像诊断技术在临床的应用和发展。
目前,加速磁共振扩散张量成像的技术主要分为两类:1)并行成像技术,并行成像技术通过多通道线圈采集具有空间敏感度编码的信号,经过解混叠算法,能够将欠采样的信号恢复得到完整的图像;然而,目前并行成像技术受到了通道线圈数目和信噪比的影响,加速倍数通常在2~3倍,并且图像的信噪比偏低。(2)压缩感知技术,压缩感知技术利用扩散图像数据的稀疏性,通过施加稀疏性约束,减少采集信号数量,加速采集;然而,过度依赖压缩感知技术往往会导致图像平滑、细节丢失等问题,并且通常需要随机性采样,难以应用于临床。
技术实现要素:
本发明的目的旨在至少在一定程度上解决上述的技术问题之一。
为此,本发明的目的在于提出一种基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法。该方法能够实现磁共振扩散张量成像的高倍加速采集,有效减少采集时间,并能够准确地估计扩散张量参数,得到高信噪比、高分辨率的扩散图像,满足了临床使用需求。
为达到上述目的,本发明实施例提出的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法,包括:基于多层同时激发预设序列对被测目标进行信号采集;通过并行成像技术对采集到的欠采样信号进行相位估计;通过估计的相位、所述采集到的欠采样信号、以及无扩散加权的参考图像,建立高斯扩散模型;根据所述高斯扩散模型整合所有方向的欠采样信号,建立用于估计扩散张量参数的目标方程;采用非线性共轭梯度算法迭代求解所述目标方程,得到扩散张量参数;根据所述扩散张量参数计算得到扩散系数和扩散加权图像。
根据本发明实施例的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法,基于多层同时激发预设序列对被测目标进行信号采集,并通过并行成像技术对采集到的欠采样信号进行相位估计,之后,通过估计的相位、采集到的欠采样信号、以及无扩散加权的参考图像,建立高斯扩散模型,然后,根据高斯扩散模型整合所有方向的欠采样信号,建立用于估计扩散张量参数的目标方程,并采用非线性共轭梯度算法迭代求解目标方程,得到扩散张量参数,最后,根据扩散张量参数计算得到扩散系数和扩散加权图像,至少具有以下优点:1)基于多层同时激发序列的高倍加速采集,能够实现磁共振扩散张量成像的高倍加速采集,有效减少采集时间;2)在高倍加速下,能够准确地估计扩散张量参数,得到高信噪比、高分辨率的扩散图像,满足了临床使用需求;3)适用于多扩散方向采集的扩散张量成像,能够为更多方向的扩散张量成像序列提供更高的加速;4)通过高斯扩散模型建立采集信号与扩散张量参数的关系,能够直接求解得到扩散张量参数,直接有效,减少了多步处理引起的误差;5)具有良好的灵活性和鲁棒性,适用于多种磁共振序列。
本发明只是以高斯模型为实例,实际上所提出的方法为一个基本方法,可以扩展到非高斯模型的整合重建,例如扩散峰度成像(diffusionkurtosisimaging,dki),伽马分布模型(gammadistributionmodel),截断高斯模型(truncatedgaussianmodel),拉伸指数模型(stretched-exponentialmodel),多高斯模型(multi-gaussianmodel),q空间成像(q-spaceimaging)等等,从而满足不同扩散成像技术的需求。
本发明附加的方面和优点将在下面的描述中部分给出,部分将从下面的描述中变得明显,或通过本发明的实践了解到。
附图说明
本发明上述的和/或附加的方面和优点从下面结合附图对实施例的描述中将变得明显和容易理解,其中:
图1是根据本发明一个实施例的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法的流程图;
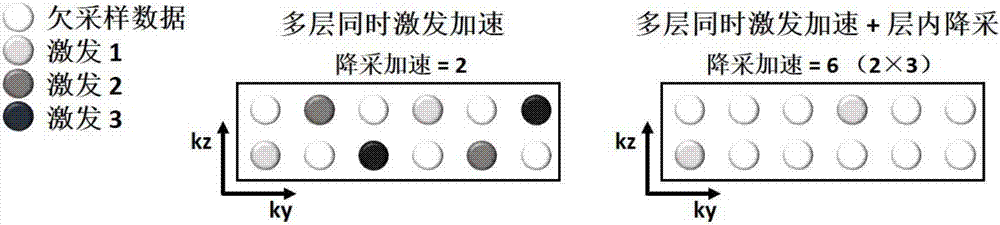
图2是本发明实施例的多层同时激发采集加速以及层内降采加速的示例图;
图3是本发明实施例的基于以高斯扩散模型为实例的整合重建流程的示例图;
图4是通过传统并行成像与本发明实施例的高斯扩散模型整合重建技术估计得到的各向异性系数对比图。
具体实施方式
下面详细描述本发明的实施例,所述实施例的示例在附图中示出,其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的,旨在用于解释本发明,而不能理解为对本发明的限制。
下面参考附图描述本发明实施例的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法。
图1是根据本发明一个实施例的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法的流程图。
如图1所示,该基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法可以包括:
s110,基于多层同时激发预设序列对被测目标进行信号采集。
需要说明的是,该预设序列可以是根据实际需求预先设定的,例如,该预设序列可以是平面回波序列等。本发明实施例并不局限于特定序列,能够灵活应用于多种磁共振扫描序列。在本发明实施例中,以多次激发平面回波序列为例进行阐述。
可以理解,多层同时激发技术是近年来开发的新型磁共振加速采集技术,技术原理是通过同时激发多层数据并同时进行数据采集来减少扫描时间。经过多层同时激发序列采集的数据,实际上是在选层方向欠采样的数据,而数据的信噪比不会有明显的下降。为此,在本步骤中,可基于多层同时激发预设序列对被测目标进行信号采集。
为了进一步加速采集,在本发明的一个实施例中,在通过并行成像技术对采集到的欠采样信号进行相位估计之前,本发明实施例的磁共振扩散成像方法还可包括:基于多次激发预设序列在相位编码方向进行欠采样采集。
举例而言,以预设序列为多次激发平面回波序列为例,在基于多层同时激发平面回波序列对被测目标进行信号采集时,还可在相位编码方向进行欠采样采集。由此,通过这两种技术结合,多次激发平面回波序列的采集能够实现高倍加速,加速倍数等于两种方法降采倍数的乘积。例如,如图2中,以一个三次激发的平面回波序列采集为例,若多层同时激发技术加速倍数为2,层内加速倍数为3,则最终数据的欠采样倍数为多层同时激发技术加速倍数与层内加速倍数的乘积,即最终数据的欠采样倍数为6,由此可见,等效于达到了6倍的采集加速。
在磁共振扩散张量成像中,每个方向都会采集到如图2所示的降采k空间数据,并且通过多通道线圈的采集会得到多通道的信号。因此,最终的采集数据是多通道,多扩散方向的欠采样三维数据。
需要说明的是,现有技术中的传统方法是通过在选层和相位编码方向使用并行成像技术进行解混叠,但对于这种高倍降采的数据,传统方法无法得到准确的图像和参数。而为了解决这个技术问题,在本发明实施例中,使用基于高斯扩散模型的整合重建方法,以得到准确的扩散张量参数,从而得到高信噪比高分辨率的扩散图像,具体实现过程可在后续实施例进行详细描述。
进一步地,在本发明的一个实施例中,在基于多层同时激发预设序列对被测目标进行信号采集之前,本发明实施例的磁共振扩散成像方法还包括:对被测目标施加预设时间的强梯度磁场,以在每次激发中进行扩散梯度编码,其中,强梯度磁场的梯度方向为扩散梯度编码方向。
具体地,在磁共振扩散成像中,可在每次激发中进行扩散梯度编码。该编码可在信号采集之前施加一段时间的强梯度磁场,该梯度方向即为扩散梯度编码方向。若在施加扩散编码梯度的同时被测目标产生了生理运动(例如,脑脊液的搏动),则会造成图像产生剧烈的相位变化。为了避免最终图像产生严重的混叠伪影,本发明实施例需对采集到的欠采样信号进行相位估计,即执行步骤s120。
s120,通过并行成像技术对采集到的欠采样信号进行相位估计。
在本步骤中,对相位误差的校正具体实现方式可为:通过线圈敏感度编码的并行成像技术,直接对采集到的欠采样信号进行重建,得到每次激发对应图像的相位。
在本发明的实施例中,可通过以下重建公式来对采集到的欠采样信号进行重建:
其中,di为需要插值的第i个线圈的k空间数据;(m,n)为对应的k空间坐标;(m',n')为在卷积核中的k空间数据的坐标;i,i'∈[1,nc];nc为通道数;g为并行成像的插值算子,可以通过预扫描得到;di'为插值使用的k空间数据。通过上述式(1),所有的k空间降采位置数据都可通过插值而得到。
为了能够得到高质量的图像,进一步地,在本发明的实施例中,在得到估计的相位之后,还可对该估计的相位进行低通图像滤波。这样,图像的相位在经过低通图像滤波之后,可以满足相位校正的需求。这是因为,扩散图像中的相位误差通常满足一个平滑的低阶多项式分布。
作为一种示例,本发明实施例可采取tukey窗在k空间进行低通滤波,然后提取对应图像域的相位,为后续的模型重建算法提供相位估计。其中,tukey窗是矩形窗和两个余弦窗的叠加,特点是采样后信号主旁瓣比高,旁瓣快速收敛。
s130,通过估计的相位、采集到的欠采样信号、以及无扩散加权的参考图像,建立高斯扩散模型。
具体地,磁共振扩散成像的信号可通过高斯扩散模型来描述,该高斯扩散模型可通过之前的估计的相位、采集到的欠采样信号、以及无扩散加权的参考图像建立而成。
在本发明的实施例中,结合本发明实施例中的采集策略,可通过以下公式建立高斯扩散模型:
上述式(2)中,ki,m可表示第m个扩散编码方向、位于i位置的k空间信号。其中,np为像素个数;
s140,根据高斯扩散模型整合所有方向的欠采样信号,建立用于估计扩散张量参数的目标方程。
在本发明的实施例中,每个扩散梯度方向的扩散图像的相位可以通过并行成像技术估计得到,无扩散加权的参考图像b0可以通过满采样得到。因此,上述式(2)中“相位”及“无扩散加权的参考图像b0”这两个变量是已知的。假设能够得到足够的k空间信号,上述式(2)中唯一的未知量只有扩散张量参数d。为了能够得到该扩散张量参数d,可通过基于高斯扩散模型的扩散张量估计得到,即可通过高斯扩散模型整合所有方向的欠采样信号,以建立用于估计扩散张量参数的目标方程。其中,可通过以下公式建立目标方程:
其中,第一项
s150,采用非线性共轭梯度算法迭代求解目标方程,得到扩散张量参数。
在得到用于估计扩散张量参数的目标方程之后,可采用非线性共轭梯度算法迭代求解该目标方程,以得到扩散张量参数。
例如,在建立高斯扩散模型之后,可通过如图3所示的流程估计扩散张量参数。在本发明实施例中,整个过程可分为两部分:1)模型重建预处理,通过并行成像以及低通滤波估计出每个扩散梯度方向的图像相位,并通过满采样得到无扩散加权的参考图像b0;2)利用非线性共轭梯度算法迭代求解目标方程,以得到扩散张量参数:基于建立的目标方程,迭代求解扩散张量参数d。每次估计的扩散张量参数d通过目标方程可以得到代价大小,若代价已经收敛(如变化小于0.1%),则停止迭代并输出该当前估计的扩散张量参数d;否则,计算目标方程的梯度,沿负梯度方向,通过设置的步长搜索使得代价最小的扩散张量参数d,并更新该扩散张量参数d,通过更新后的扩散张量参数d再次重复上述步骤,直到该代价收敛。其中,收敛时所对应的d,即为待求解的扩散张量参数。
s160,根据扩散张量参数计算得到扩散系数和扩散加权图像。
在得到扩散张量参数之后,通过该扩散张量参数可以得到需要的扩散加权图像、各向异性分数、平均扩散系数以及扩散张量特征方向参数等重要图像指标。
综上,在提出的基于以高斯扩散模型为实例整合重建的过程中,所有扩散编码方向的欠采样数据都会在迭代重建中同时使用,隐性地利用了扩散成像中不同方向数据的相关性。传统的扩散张量成像需要首先重建每个方向的数据,然后通过高斯扩散模型通过多参数回归算法得到扩散张量。而本发明实施例中跳过了重建单独图像的过程,通过整合重建直接估计扩散张量参数,减少了未知量个数,提高了扩散张量参数估计的准确性。例如,图4是通过传统并行成像与本发明实施例的高斯扩散模型整合重建技术估计得到的各向异性系数对比图。如图4所示,以对32个扩散梯度方向的8倍加速采集数据为例(其中,多层激发加速倍数为2,层内降采加速倍数为4),本发明实施例提出的基于以高斯扩散模型为实例整合重建的扩散成像方法大大提高了在高倍加速下扩散张量参数估计的准确性与信噪比。
根据本发明实施例的基于以高斯扩散模型为实例整合重建的磁共振扩散成像方法,基于多层同时激发预设序列对被测目标进行信号采集,并通过并行成像技术对采集到的欠采样信号进行相位估计,之后,通过估计的相位、采集到的欠采样信号、以及无扩散加权的参考图像,建立高斯扩散模型,然后,根据高斯扩散模型整合所有方向的欠采样信号,建立用于估计扩散张量参数的目标方程,并采用非线性共轭梯度算法迭代求解目标方程,得到扩散张量参数,最后,根据扩散张量参数计算得到扩散系数和扩散加权图像,至少具有以下优点:1)基于多层同时激发序列的高倍加速采集,能够实现磁共振扩散张量成像的高倍加速采集,有效减少采集时间;2)在高倍加速下,能够准确地估计扩散张量参数,得到高信噪比、高分辨率的扩散图像,满足了临床使用需求;3)适用于多扩散方向采集的扩散张量成像,能够为更多方向的扩散张量成像序列提供更高的加速;4)通过高斯扩散模型建立采集信号与扩散张量参数的关系,能够直接求解得到扩散张量参数,直接有效,减少了多步处理引起的误差;5)具有良好的灵活性和鲁棒性,适用于多种磁共振序列。
在本发明的描述中,需要理解的是,术语“第一”、“第二”仅用于描述目的,而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此,限定有“第一”、“第二”的特征可以明示或者隐含地包括至少一个该特征。在本发明的描述中,“多个”的含义是至少两个,例如两个,三个等,除非另有明确具体的限定。
在本说明书的描述中,参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中,对上述术语的示意性表述不必须针对的是相同的实施例或示例。而且,描述的具体特征、结构、材料或者特点可以在任一个或多个实施例或示例中以合适的方式结合。此外,在不相互矛盾的情况下,本领域的技术人员可以将本说明书中描述的不同实施例或示例以及不同实施例或示例的特征进行结合和组合。
尽管上面已经示出和描述了本发明的实施例,可以理解的是,上述实施例是示例性的,不能理解为对本发明的限制,本领域的普通技术人员在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。
- 还没有人留言评论。精彩留言会获得点赞!