基于牛顿下山法的多层悬臂梁材料的薄膜杨氏模量提取方法与流程

本发明公开了基于牛顿下山法的多层悬臂梁材料的薄膜杨氏模量提取方法，借助于多层悬臂梁材料的物理性质并通过计算机辅助设计的算法来测试或分析材料，属于测量、测试以及计算、推算、计数的技术领域。

背景技术：

微电子机械系统(mems，micro-electro-mechanicalsystems)是指在微电子技术基础上发展起来的结合了电、力、热、光、电磁和流体等技术的尖端科技。近年来，cmosmems技术被广泛应用于mems加工中，制造出了多种多样的微器件和微系统。众所周知，诸如杨氏模量、残余应力等材料力学参数对mems器件的结构和功能有很大的影响。然而，对于cmosmems工艺薄膜材料而言，在不同的加工工艺条件下，即使相同的材料也往往会表现出明显不同的材料特性，因此，需要准确地测量出这些力学参数。但是，一方面由于尺寸相对较小，薄膜材料的材料参数难以利用经典的宏观表征技术进行实验测量；另一方面，cmosmems器件往往使用多层薄膜结构，将已有的测试单层薄膜材料力学参数方法应用到多层薄膜材料参数测量上却并不容易。因此，建立工艺兼容的多层薄膜材料力学参数在线测试结构和测试方法对于监测mems薄膜材料力学特性、预测和优化产品性能进而保证产品性能可靠、均匀一致并且长期稳定具有非常重要的意义。对于特定的在线测试结构和方法，所要求的标准如下：测试结构的加工工艺必须与被监测工艺相兼容，测试结构几何简单、占用面积小、坚固可重复使用、测量方法简单直接。

传统的杨氏模量提取方法为牛顿法，但是牛顿法对初值的选取具有严格的要求，而且牛顿法只有局部的收敛性。本申请旨在应用改进的牛顿下山法提取不等宽多层悬梁臂材料的薄膜杨氏模量，通过扩大初值选取范围改进传统牛顿算法的收敛性并提升迭代精度。

技术实现要素：

本发明的发明目的是针对上述背景技术的不足，提供了基于牛顿下山法的多层悬臂梁材料的薄膜杨氏模量提取方法，扩大了初值选取的范围且尽可能保留了牛顿法的收敛速度，解决了当前牛顿法提取各层杨氏模量值不收敛或者只在部分区域收敛的技术问题，克服了牛顿法对初值要求严格导致实际应用中难以给出确保的收敛初值这一缺陷。

本发明为实现上述发明目的采用如下技术方案：

本发明使用多层悬臂梁作为测试结构，利用多层微机械梁谐振模型对多层薄膜材料杨氏模量进行提取，包括如下6个基本步骤。

1)使用多层悬臂梁作为测试结构并利用多层微机械梁谐振模型对多层薄膜材料杨氏模量进行提取需要推导出悬臂梁一阶谐振频率与尺寸以及力学参数之间的函数关系：

式(1)中，频率值的下标j表示第j层材料，1表示第一阶谐振频率，cf表示边界条件为悬臂梁，fj1cf为悬臂梁一阶谐振频率，ej为第j层薄膜材料的杨氏模量，ij为第j层薄膜材料在横截面上的面积aj关于中性轴的转动惯量，ρj为第j层薄膜材料的材料密度。

2)本算法提取的对象是不等宽多晶硅-金(polysilicon-au)双层悬臂梁模型，该结构采用memscap公司的polymumps标准表面微加工工艺，通过多普勒激光谐振器测量其谐振频率，本发明规定了所有的多层悬臂梁结构第一层都具有相同的宽度，因此，这里只要保证第2层至最顶层的宽度组合不完全相同即可，若需提取n层悬臂梁的杨氏模量，需要求解至少n个n层悬臂梁模型的杨氏模量，需测出每一个n层悬臂梁模型的一阶谐振频率的值。

3)本发明首先通过牛顿法迭代尝试将式(1)中杨氏模量与其它各参数的关系反解出来，通过等式变换将其化简成牛顿迭代法通用形式的方程，将测出的n组一阶谐振频率带入方程中便可得到牛顿迭代的最初形式，即，n维的多元函数非线性方程组：

式(2)中，f1cf(e1,e2,...,en,b12,b13,...,b1n,lm)表示长度为lm而宽度组合为b12,b13,...,b1n的n层悬臂梁模型的一阶谐振频率与各层薄膜材料杨氏模量的关系，f1cf(e1,e2,...,en,b22,b23,...,b1n,lm)表示长度为lm而宽度组合为b22,b23,...,b1n的n层悬臂梁模型的一阶谐振频率与各层薄膜材料杨氏模量的关系，f1cf(e1,e2,…,en,bn2,bn3,…,bnn,lm)表示长度为lm而宽度组合为bn2,bn3,…,bnn的n层悬臂梁模型的一阶谐振频率与各层薄膜材料杨氏模量的关系，ftm1、ftm2、ftmn分别为第1个、第2个、第n个n层悬臂梁模型一阶谐振频率的测量值。

4)牛顿迭代法需选取合适的迭代初值，通过memscap公布的数据以及其它文献中给出的相应参数值确定迭代初值的范围，然后在此量级下确定初值，利用迭代公式(3)得到迭代结果。通过该方法得到的结果虽然在单根附近的收敛速度较快但是计算复杂且全局收敛性很差，

x^(k+1)＝x^(k)-f′(x^(k))^-1f(x^(k))(k＝0,1,…)(3)。

5)对上述牛顿迭代法的迭代公式进行优化，采用牛顿下山法迭代，迭代公式修改为式(4)，首先，通过改变下山因子使得其获得不同的迭代次数；其次，通过改变残量精度以及根的误差限使下山法获得更高的迭代精度；最后，为了验证下山法的收敛性能，可以选择不同域的迭代初值从多个方向迭代，通过放宽初值，验证几次迭代后是否将原本收敛域外的初值拉入收敛域内，

x^(k)、x^(k+1)为第k次、第k+1次的迭代值，f(x^(k))为根据第k次迭代值求得的由式(2)简化得到的符合牛顿迭代法通用形式的方程组的解，f′(x^(k))为f(x^(k))的一阶导数，λ为下山因子。

6)最后，取不同尺寸的双层悬臂梁，检验该算法的鲁棒性，验证在同一量级下其它尺寸的收敛情况，验证是否有不收敛的跳跃间断点，将获得的结果与memscap公布的数据以及其它文献中给出的相应参数值对比，然后比较牛顿迭代和牛顿下山法运算精度偏差的大小。

本发明采用上述技术方案，具有以下有益效果：

(1)本发明中提出采用牛顿下山法优化经典牛顿迭代公式，在收敛速度和收敛结果不变的约束下设定残量精确度进而截取迭代值有效位数，在牛顿下山法的迭代值满足残量精确度所受约束时采用经典牛顿法逼近满足根误差限的收敛解，该方法扬长避短，尽可能保留了牛顿法的收敛速度但又改进了牛顿法的收敛性，通过改进牛顿下山法的迭代精度获得更快的迭代速度，减小算法的时间复杂度，对得到高收敛性的力学参数具有实用的意义。

(2)通过多个方向迭代将收敛域外的初值拉入收敛域，扩大了初值选取的范围，改善了经典牛顿法因初值选择太过苛刻而局部收敛的缺陷，因此，本申请公开的方法更具适用性。

附图说明

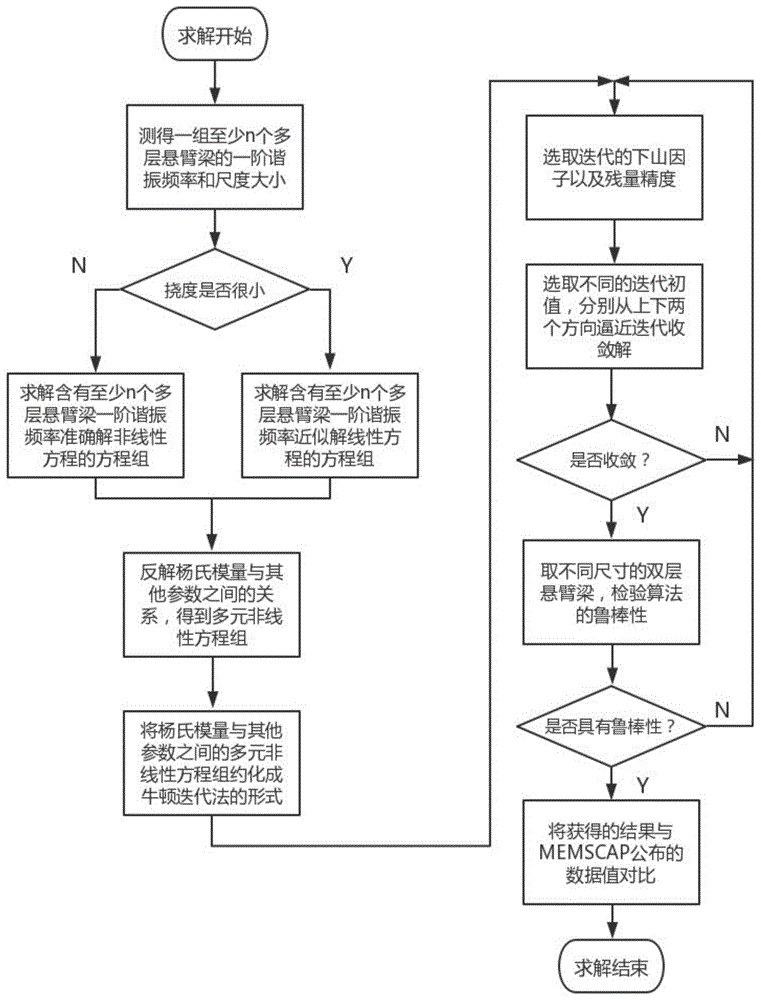
图1为基于牛顿下山法的多层悬臂梁薄膜杨氏模量提取的流程图。

图2为牛顿下山法具体实现的流程图。

具体实施方式

下面结合附图对发明的技术方案进行详细说明。

(一)悬臂梁的物理量介绍

当薄膜宽度与其厚度满足bi＜5hi即窄梁时，等效杨氏模量就是杨氏模量ei其本身；当薄膜宽度与其厚度满足bi≥5hi即宽梁时，等效杨氏模量是一个关于杨氏模量和泊松比vi的关系式，即则等效杨氏模量关于薄膜厚度及其宽度之间的关系为：

等效残余应力为经历释放工艺之前(即未发生形变时)，梁的长度为l。第i层薄膜材料的宽度为wi，厚度为hi，材料密度为ρi，杨氏模量为ei。多层梁的底面(即衬底的顶面)在z轴上位置为z0，z0＝0，从下至上第i层薄膜材料的顶面在z轴上的位置为zi，则：

中性面高度zc为：

第i层薄膜材料在横截面上的面积关于中性轴的转动惯量ii为：

定义微机械薄膜梁的弯曲刚度为线性密度为轴向载荷为即：

其中，ai为第i层薄膜材料在横截面上的面积。

(二)双层悬臂梁一阶谐振频率与材料参数的关系

对于释放后保持平直状态的双层微机械悬臂梁，其各阶谐振频率的近似解析公式为：

式(12)中，kil满足关系式cos(kil)cosh(kil)＝-1，k1l＝1.875，k2l＝4.694，k3l＝7.855，...，当i≥2时，有近似关系kil≈(i-1/2)。将该情况下第一阶谐振频率的近似解析公式单独列出来，为：

式(13)中，频率值的下标1表示第一阶谐振频率，cf表示边界条件为悬臂梁。

对于由n层薄膜材料构成的多层悬臂梁，有n个需要求解的材料力学特性参数，这时需要至少n个多层悬臂梁，其长度在理论上没有限制要求(为了计算方便本发明采取统一长度设计多层悬臂梁)，并且这一组多层悬臂梁的n层薄膜材料的宽度至少具有n种不同类型的组合：假设第j根多层梁从下至上各层的宽度分别为bj1，bj2，...，bjn，...(1≤j≤n)，另一根梁即第k根多层梁从下至上各层的宽度分别为bk1，bk2，...，bkn，...(1≤k≤n，k≠j)，那么，向量(bj1，bj2，...，bjn，...)和向量(bk1，bk2，...，bkn，...)必须线性无关。由于本发明规定了所有的多层悬臂梁结构第一层都具有相同的宽度，因此，这里只要保证第2层至最顶层的宽度组合不完全相同即可。通过上述至少n个多层悬臂梁可以得到至少n个一阶谐振频率，可以得到一个由至少n个线性方程构成的方程组：

(三)牛顿下山法迭代过程

欲使用牛顿法需将式(14)中杨氏模量与其它各参数的关系反解出来，通过等式变换将其化简成牛顿迭代法通用的形式：

式(15)中，f1,…,fn均为(x1,x2,…xn)的多元函数。

若用向量记号记为：

x＝(x1,x2,…,xn)^t∈rⁿ，f＝(f1,f2,…fn)^t(16)，

式(16)所示向量标记的方程组有可能有一个解或者多个解，也可能有无穷解或者无解，除特殊方程外，一般不能采用直接法求得精确解，目前，只能采用迭代近似求解，根据不同思想构造迭代收敛于x^*的迭代序列x^k，(k＝0,1,…)。

给出方程的一个近似根将函数f(x)的分量fi(x)(i＝1,…n)在x^(k)处用多元函数泰勒展开并取其线性部分，可以将函数f(x)表示为f(x)≈f(x^(k))+f′(x^(k))(x-x^(k))，然后，令上式右端等于零可得线性方程组：

f′(x^(k))(x-x^(k))＝-f(x^(k))(17)，

其中，

称f′(x)为雅可比矩阵，求解式(17)，将解记为x^(k+1)。牛顿法的迭代公式为：

x^(k+1)＝x^(k)-f′(x^(k))^-1d(x^(k))(k＝0,1,…)(19)，

牛顿下山法是将牛顿法中的迭代公式修改为：

其中，λ被称为下山因子，下山因子的选取应满足|f(x^(k+1))|<|f(x^(k))|这一不等式的成立，当|f(x^(k))|<ε1或者|x^(k+1)-x^(k)|<ε2就停止迭代，且取x^*≈x^(k)，其中，ε1、ε2为事先设定的精度，ε1为残量精确度，ε2为根误差限；否则，再减λ后继续迭代，按上述的迭代过程计算得到一个以零为下界的严格单调下降的函数值序列，这个方法称为牛顿下山法。

(四)应用改进的牛顿下山法提取多层悬梁臂材料的薄膜杨氏模量

本申请公开的基于牛顿下山法的多层悬臂梁材料的薄膜杨氏模量提取方法如图1所示，包括以下5大步骤。

步骤1、对于n层薄膜材料构成的多层悬臂梁而言，为提取其各层薄膜杨氏模量，需要测量一组至少n个n层悬臂梁的一阶谐振频率，n个n层悬臂梁的长度以及第一层薄膜的宽度相同但第2层至最顶层薄膜的宽度组合不同，记录n个n层悬臂梁一阶谐振频率的测量值以及薄膜的尺寸参数。

步骤2、对于挠度很小的多层悬臂梁，建立求解至少n个n层悬臂梁一阶谐振频率近似解线性方程的方程组，对于挠度较大的多层悬臂梁，建立求解至少n个n层悬臂梁一阶谐振频率准确解非线性方程的方程组，反演杨氏模量与一阶谐振频率的关系得到多元非线性方程组，将多元非线性方程组化简为牛顿迭代形式的方程组f(x)。

步骤3、引入了满足|f(x^(k+1))|<|f(x^(k))|这一约束(f(x^(k))中的每个f(x^(k))都满足这一约束)的下山因子λ、残量精确度ε1、根误差限ε2，对于步骤2获取的牛顿迭代形式的方程组进行如图2所示的迭代求解过程：

根据第k次迭代解x^(k)求得牛顿迭代形式的方程组f(x)在当前迭代解处的一阶导数f′(x^(k))，再根据引入了下山因子的迭代公式求解第k+1次迭代解x^(k+1)；

|f(x^(k+1))|<|f(x^(k))|时，以第k次迭代解为第k+1次迭代解，否则，减小下山因子的取值后依据引入了下山因子的迭代公式求解第k+1次迭代解x^(k+1)，将第k+1次迭代解赋值给第k次迭代解，在|f(x^(k))|<ε1时结束迭代，而在|f(x^(k))|≥ε1时调整残量精确度ε1的取值进而对迭代解的有效位数进行截取，重新判断第k+1次迭代解、第k次迭代解是否满足|f(x^(k+1))|<|f(x^(k))|这一约束；

在第k+1次迭代解、第k次迭代解满足|f(x^(k+1))|<|f(x^(k))|这一约束时，采用经典牛顿迭代公式继续迭代求解直至|x^(k+1)-x^(k)|<ε2时停止迭代。

步骤4，选取不同域的迭代初值后分别从上下两个方向逼近收敛解，若上下两个方向都收敛在满足根误差限的固定值，将收敛域外的初值拉入收敛域内，若上下两个方向的迭代解波动或者跳跃，重新设定残量精确度。

步骤5，取不同尺寸的双层悬臂梁，检验该算法的鲁棒性，验证在同一量级下其它尺寸双层悬臂梁薄膜杨氏模量提取值的收敛情况，验证是否有不收敛的跳跃间断点，有不收敛的跳跃间断点时重新设定残量精确度，没有不收敛的跳跃间断点时对比获得的结果与memscap公布的数据以及其它文献中给出的相应参数值，然后比较牛顿迭代和牛顿下山法运算精度偏差的大小。

牛顿下山法优化原始的方法，该方法扬长避短，扩大了初值选取的范围，同时尽可能保留了牛顿法的收敛的速度。申请人已经成功使用matlab完成利用多层微机械梁谐振模型对多层薄膜材料杨氏模量进行提取的编程，仿真结果表明：与经典牛顿法相比，本申请明显改善了经典牛顿法的收敛性问题，大大提高了杨氏模量的提取精度，算法有着更低的时间复杂度和空间复杂度，该优化算法对于得到高收敛性的力学参数具有实用意义。

需要说明的是，上述实施例仅仅是本发明的较佳实施例，并没有用来限定本发明的保护范围，在上述技术方案的基础上做出的等同替换或者替代均属于本发明的保护范围。