一种谐波发射水平评估方法及装置与流程

1.本发明涉及电能质量数据估计领域，具体是一种谐波发射水平评估方法及装置。


背景技术：

2.随着新能源、直流输电和大量含有电力电子设备的非线性负荷接入电网，使得电网呈现多源、非线性特征，从源-网-荷三个方面日趋电力电子化，从而导致谐波问题更加复杂化、影响范围更广。对用户侧和系统侧谐波发射水平的精确估计，是如今急需解决的问题，对用户和系统的谐波责任划分有重要的意义。
3.当前国内外谐波发射水平的评估的关键在于系统谐波阻抗的准确估计。系统谐波阻抗指在某一谐波频率下从电力接入点值电源侧的谐波阻抗，数值上等于系统侧谐波电压与系统侧谐波电流的比值。系统谐波阻抗主要取决于发电机、变压器、导体的横截面积和长度。
4.计算谐波阻抗的方法主要有两类，即侵入式和非侵入式方法。前者测量由注入电网的谐波电流产生的谐波电压，然而这种方法可能会降低系统的运行；后者利用共同耦合点(pcc)上可测量的谐波电流和谐波电压来估计谐波阻抗，对电力系统没有任何不利影响。因此，非侵入式方法引起了极大的关注。
5.近些年来，国内外的非侵入式方法主要有以下类别：波动量法是最早提出的计算系统谐波阻抗的方法，但是却受到背景谐波的影响；线性回归法依赖pcc处谐波电压和谐波电流符合线性关系，难以在实际工程中实现；随机独立矢量法要求用户侧谐波阻抗远大于系统侧，当用户侧谐波阻抗较低时方法失效；独立分量法是近些年来新兴的方法，但是当pcc两侧谐波阻抗幅值相近时可能会出现数据分离失效的情况。


技术实现要素：

6.针对现有技术存在的不足，本发明提出的一种谐波发射水平评估方法及装置，可以改进谐波发射水平的估计效果，降低估计误差。
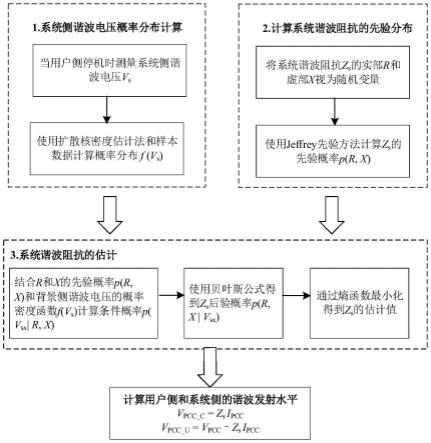
7.一种谐波发射水平评估方法，包括如下步骤：
8.测量用户侧停机时系统侧谐波电压vs，使用扩散核密度估计算法计算系统侧谐波电压的概率密度函数f(vs)，将系统谐波阻抗zs的实部r和虚部x视为随机变量，利用jeffrey先验算法估计r和x的先验概率p(r，x)，结合r和x的先验概率p(r，x)和系统侧谐波电压的概率密度函数f(vs)计算条件概率p(v
sx
|r，x)；
9.根据先验概率p(r，x)、概率密度函数f(vs)和条件概率p(v
sx
|r，x)计算得到r和x的后验概率p(r，x|v
sx
)，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值；
10.根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平。
11.进一步的，使用扩散核密度估计算法，计算系统侧谐波电压的概率密度函数f(vs)，具体包括：以如下核密度估计表达式计算vs的概率密度函数：
[0012][0013]
式中，v
sxi
为测得的系统侧谐波电压实部的样本值，n为样本容量，h为带宽，k为核函数。
[0014]
进一步的，带宽h的最优带宽为h*，采用如下公式计算：
[0015][0016]
式中，kd(
·
)为扩散核函数，n代表高斯核密度估计的初始条件系数，x和t为kd(
·
)中的随机变量，a(x)、b(x)为在定义域中具有二阶导数的任何正函数。
[0017]
进一步的，利用jeffrey先验算法估计r和x的先验概率p(r，x)，具体包括：将zs的先验分布视为正态分布，参数为(μ，σ2)，利用jeffrey先验方法估计参数(μ，σ2)，(μ，σ2)的分布如下：
[0018][0019]
根据贝叶斯公式，(μ，σ2)的联合后验分布由如下公式获得
[0020][0021]
式中，种分别是μ和σ2的数学期望，根据标准化熵损失函数的定义，参数μ和σ2的估计取数学期望值，得到μ和σ2的估计值如下：
[0022][0023]
式中，e1代表后验概率的数学期望，和分别为μ和σ2的估计值，zs的先验分布为对先验分布函数求导得到r和x的先验概率p(r，x)。
[0024]
进一步的，结合r和x的先验概率p(r，x)和系统侧谐波电压的概率密度函数f(vs)计算条件概率p(v
sx
|r，x)，具体包括：将随机变量r，x的先验分布记为：
[0025][0026]
通过下式计算条件概率：
[0027][0028]
式中，n为用于计算条件概率样本数据的长度，p(v
sx
(t|r，x))代表v
sx
(r，x)中第t
个元素的概率值。
[0029]
进一步的，根据先验概率p(r，x)、概率密度函数f(vs)和条件概率p(v
sx
|r，x)，使用贝叶斯公式计算r和x的后验概率p(r，x|v
sx
)：
[0030][0031]
计算r，x的后验概率值，f(v
sx
)视为常数，上式写为：
[0032]
p(r，x|v
sx
)＝λp(v
sx
|r，x)p(r，x)
[0033]
式中，λ表示任一非零实数。
[0034]
进一步的，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值具体包括：
[0035]
根据r和x的后验概率p(r，x|v
sx
)得到r和x的联合概率密度函数π(r，x|v
sx
)，根据r和x的联合概率密度函数得到边缘概率密度函数π(r|v
sx
)和π(x|v
sx
)：
[0036][0037]
式中，π(r，x|v
sx
)为r和x的联合概率密度函数，π(r|v
sx
)和π(x|v
sx
)分别为r和x的边缘概率密度函数；
[0038]
通过计算边缘概率密度函数的数学期望得到系统谐波阻抗实部和虚部的估计值：
[0039][0040]
式中，z
sx
和z
sy
分别为系统谐波阻抗实部和虚部的估计值，根据z
sx
和z
sy
计算系统谐波阻抗zs的估计值，即zs＝z
sx
+jz
sy
。
[0041]
进一步的，根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平，具体包括：根据如下公式计算用户侧和系统侧谐波发射水平：
[0042]vpcc_c
＝z
sipcc
[0043]vpcc_u
＝v
pcc-z
sipcc
[0044]
其中v
pcc_c
为用户侧的谐波发射水平，v
pcc_u
为系统侧的谐波发射水平，i
pcc
为共同耦合点处的谐波电流，v
pcc
为共同耦合点处的谐波电压。
[0045]
一种谐波发射水平评估装置，包括
[0046]
条件概率计算模块，用于测量用户侧停机时系统侧谐波电压vs，使用扩散核密度估计算法计算系统侧谐波电压的概率密度函数f(vs)，将系统谐波阻抗zs的实部r和虚部x视为随机变量，利用jeffrey先验算法估计r和x的先验概率p(r，x)，结合r和x的先验概率p(r，x)和系统侧谐波电压的概率密度函数f(vs)计算条件概率p(v
sx
|r，x)；
[0047]
系统谐波阻抗估计值计算模块，用于根据先验概率p(r，x)、概率密度函数f(vs)和条件概率p(v
sx
|r，x)计算得到r和x的后验概率p(r，x|v
sx
)，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值；
[0048]
系统谐波阻抗计算模块，用于根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平。
[0049]
进一步的，所述系统谐波阻抗估计值计算模块根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平，具体包括：根据如下公式计算用户侧和系统侧谐波发射水平：
[0050]vpcc_c
＝z
sipcc
[0051]vpcc_u
＝v
pcc-z
sipcc
[0052]
其中v
pcc_c
为用户侧的谐波发射水平，v
pcc_u
为系统侧的谐波发射水平，i
pcc
为共同耦合点处的谐波电流，v
pcc
为共同耦合点处的谐波电压。
[0053]
一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，处理器执行计算机程序时实现如上所述的谐波发射水平评估方法。
[0054]
一种非暂态计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现如上所述的谐波发射水平评估方法。
[0055]
相比现有技术，本发明只需要背景谐波的概率密度函数，使用实测数据修正先验概率，因此受背景谐波的影响较小；并且本发明使用贝叶斯模型，和pcc处谐波电压和谐波电流的关系无关。仿真分析和场地实测数据都表明，无论用户侧谐波阻抗远大于系统侧，或是pcc两侧谐波阻抗幅值相近，本发明的方法都具有较好的结果。综上所述，本发明能够改进现有技术存在的问题，降低估计结果的误差，准确估计用户侧和系统侧的谐波发射水平。
附图说明
[0056]
图1为本发明谐波发射水平评估方法其中一个实施例的流程示意图；
[0057]
图2为本发明谐波责任划分系统模型图。
具体实施方式
[0058]
为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0059]
如图1所示，本发明实施例提供的一种谐波发射水平评估方法，图2为谐波责任划分系统模型图，所述方法包括以下步骤：
[0060]
s1：用户侧停机，测量系统侧谐波电压vs；先将用户侧停机，断开系统侧和用户侧的连接，之后在电网公共耦合点测量谐波电压，此时的谐波电压只包含系统侧谐波vs，保证了测量的准确性。
[0061]
s2：使用扩散核密度估计算法，计算系统侧谐波电压的概率密度函数f(vs)，具体的，以如下核密度估计表达式计算vs的概率密度函数：
[0062][0063]
式中，v
sxi
为测得的系统侧谐波电压实部的样本值，n为样本容量，h为带宽，k为核函数。为了得到最优带宽h*，引入线性扩散参数其中a(x)，b(x)为任意在定义域内具有二阶导数的正函数。最优带宽h*可以用如下公式计算：
[0064][0065]
式中，其中kd(
·
)为扩散核函数，n代表高斯核密度估计的初始条件系数，x和t为kd(
·
)中的随机变量，a(x)、b(x)为在定义域中具有二阶导数的任何正函数。
[0066]
s3：将系统谐波阻抗zs的实部r和虚部x视为随机变量，利用jeffrey先验算法估计r和x的先验概率p(r，x)。
[0067]
具体的，将系统谐波阻抗zs的实部r和虚部x视为随机变量，根据中心极限定理，大量zs可以认为符合正态分布，因此本发明实施例将zs的先验分布视为正态分布，参数为(μ，σ2)，利用jeffrey先验方法估计参数(μ，σ2)。首先认为(μ，σ2)的分布如下：
[0068][0069]
根据贝叶斯公式，(μ，σ2)的联合后验分布可以由如下公式获得
[0070][0071]
式中，种分别是μ和σ2的数学期望，之后根据标准化熵损失函数的定义，参数μ和σ2的估计取数学期望值，因此得到μ和σ2的估计值如下
[0072][0073]
式中，e1代表后验概率的数学期望，和分别为μ和σ2的估计值。因此，zs的先验分布为对先验分布函数求导得到r和x的概率密度函数(即先验概率)p(r，x)。
[0074]
s4：结合r和x的先验概率p(r，x)和系统侧谐波电压的概率密度函数f(vs)计算条件概率p(v
sx
|r，x)。
[0075]
具体的，将随机变量r，x的先验分布记为
[0076][0077]
根据上式得到r，x的先验分布π(r，x)，之后通过下式计算条件概率：
[0078][0079]
式中，n为用于计算条件概率样本数据的长度，p(v
sx
(t|r，x))代表v
sx
(r，x)中第t个元素的概率值，可以从f(vs)中获得。
[0080]
s5：根据先验概率p(r，x)、概率密度函数f(vs)和条件概率p(v
sx
|r，x)计算得到r和
x的后验概率p(r，x|v
sx
)，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值。
[0081]
具体的，根据先验概率p(r，x)、概率密度函数f(vs)和条件概率p(v
sx
|r，x)，使用贝叶斯公式计算r和x的后验概率p(r，x|v
sx
)：
[0082][0083]
计算r，x的后验概率值，f(v
sx
)可以视为常数，因此上式可以写为：
[0084]
p(r，x|v
sx
)＝λp(v
sx
|r，x)p(r，x)
[0085]
式中，λ表示任一非零实数。
[0086]
根据统一化熵损失函数的定义，当参数的估计值等于其数学期望时，熵函数的损失最小，参数值的估计最准确。因此，系统谐波阻抗的估计值应为其后验概率p(r，x|v
sx
)的数学期望，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值，具体包括：
[0087]
根据r和x的后验概率p(r，x|v
sx
)得到r和x的联合概率密度函数π(r，x|v
sx
)，之后根据r和x的联合概率密度函数得到边缘概率密度函数π(r|v
sx
)和π(x|v
sx
)：
[0088][0089]
式中，π(r，x|v
sx
)为r和x的联合概率密度函数，π(r|v
sx
)和π(x|v
sx
)分别为r和x的边缘概率密度函数；
[0090]
之后通过计算边缘概率密度函数的数学期望得到系统谐波阻抗实部和虚部的估计值：
[0091][0092]
式中，z
sx
和z
sy
分别为系统谐波阻抗实部和虚部的估计值，根据z
sx
和z
sy
计算系统谐波阻抗zs的估计值，即zs＝z
sx
+jz
sy
。
[0093]
s6、根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平。
[0094]
得到系统谐波阻抗zs的估计值后，根据如下公式计算用户侧和系统侧谐波发射水平：
[0095]vpcc_c
＝z
sipcc
[0096]vpcc_u
＝v
pcc-z
sipcc
[0097]
其中v
pcc_c
为用户侧的谐波发射水平，v
pcc_u
为系统侧的谐波发射水平。i
pcc
为pcc处的谐波电流，v
pcc
为pcc处的谐波电压。
[0098]
本发明实施例还提供一种谐波发射水平评估装置，包括：
[0099]
条件概率计算模块，用于测量用户侧停机时系统侧谐波电压vs，使用扩散核密度估计算法计算系统侧谐波电压的概率密度函数f(vs)，将系统谐波阻抗zs的实部r和虚部x视为随机变量，利用jeffrey先验算法估计r和x的先验概率p(r，x)，结合r和x的先验概率p(r，x)和系统侧谐波电压的概率密度函数f(vs)计算条件概率p(v
sx
|r，x)；
[0100]
系统谐波阻抗估计值计算模块，用于根据先验概率p(r，x)、概率密度函数f(vs)和
条件概率p(v
sx
|r，x)计算得到r和x的后验概率p(r，x|v
sx
)，根据r和x的后验概率p(r，x|v
sx
)计算得到系统谐波阻抗zs的估计值；
[0101]
系统谐波阻抗计算模块，用于根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平。
[0102]
所述系统谐波阻抗计算模块根据系统谐波阻抗zs的估计值计算用户侧和系统侧的谐波发射水平，具体包括：根据如下公式计算用户侧和系统侧谐波发射水平：
[0103]vpcc_c
＝z
sipcc
[0104]vpcc_u
＝v
pcc-z
sipcc
[0105]
其中v
pcc_c
为用户侧的谐波发射水平，v
pcc_u
为系统侧的谐波发射水平，i
pcc
为共同耦合点处的谐波电流，v
pcc
为共同耦合点处的谐波电压。
[0106]
实验数据验证
[0107]
为了说明本发明的技术效果，采用仿真实验数据计算本发明和其他发明的谐波发射水平估计误差。使用诺顿等效电路模型，用户侧谐波电流源幅值设置为50a，相角设置为30
°
。系统侧谐波电流源幅值设置为50q a，q为变量，相角设置为10
°
。系统侧谐波阻抗和用户侧谐波阻抗设置为5∠30
°
ω。表1和表2给出了本发明和其他发明方法的用户侧和系统侧谐波发射水平估计误差。其中，方法1为波动量法，方法2为线性回归发，方法3为随机独立矢量法，方法4为独立分量法，方法5为本发明提出的方法。
[0108]
表1用户侧谐波发射水平估计误差
[0109][0110]
表2系统侧谐波发射水平估计误差
[0111][0112]
从表1和表2可以看出，本发明提出的方法对谐波发射水平的估计误差显著低于其他发明方法，这是由于本发明首先测量系统侧谐波电压vs，使用扩散核密度估计算法得到vs的概率密度函数f(vs)；之后使用jeffrey算法得到系统谐波阻抗zs的先验分布，这期间不需要任何zs的先验信息；最后使用贝叶斯公式得到zs的后验分布，进而得到pcc两侧的谐波发射水平。本发明只需要背景谐波的概率密度函数，使用实测数据修正先验概率，因此受背景谐波的影响较小。并且本发明使用贝叶斯模型，和pcc处谐波电压和谐波电流的关系无关。
[0113]
本发明提出的方法、线性回归法和随机独立矢量法，在谐波责任划分系统模型图上对用户侧谐波发射水平的估计效果误差对比如表3所示：
[0114]
表3用户侧谐波发射水平的估计效果
[0115][0116]
从表3可以看出，本发明提出的方法对用户侧谐波发射水平的估计效果误差要显著优于现有的线性回归法和随机独立矢量法。
[0117]
本领域内的技术人员应明白，本技术的实施例可提供为方法、系统、或计算机程序产品。因此，本技术可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本技术可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。
[0118]
本技术是参照根据本技术实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产
生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0119]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0120]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0121]
最后应当说明的是：以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员应当理解：依然可以对本发明的具体实施方式进行修改或者等同替换，而未脱离本发明精神和范围的任何修改或者等同替换，其均应涵盖在本发明的权利要求保护范围之内。