基于ELM的自动驾驶列车车速跟随的控制方法与流程

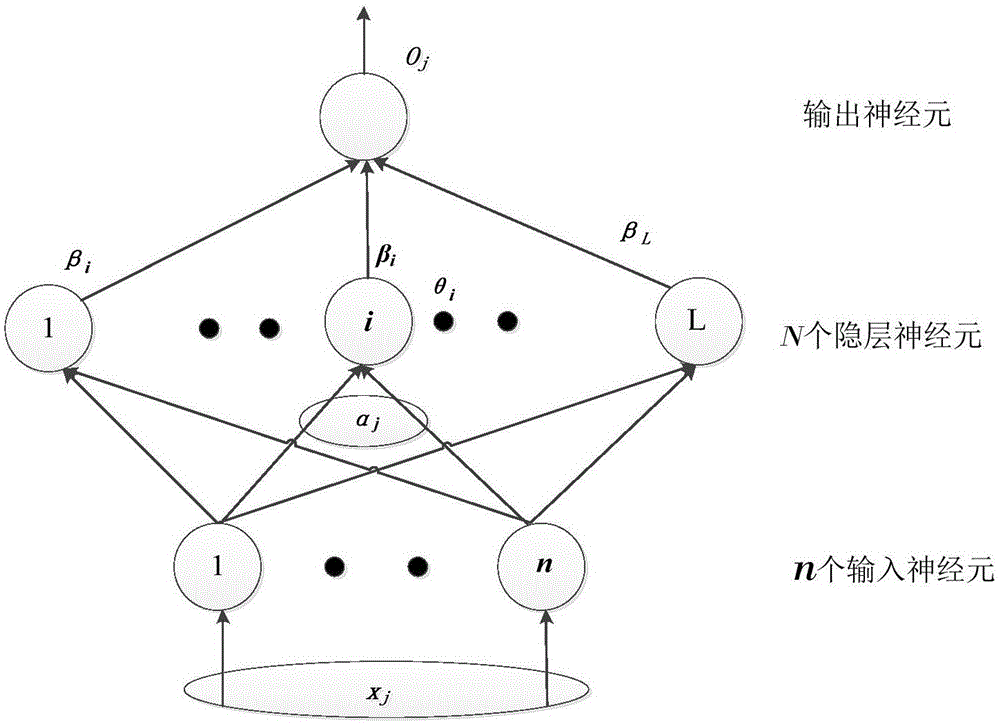
本发明属于列车自动驾驶技术领域，具体涉及一种基于elm(极限学习机)的自动驾驶列车车速跟随的控制方法。

背景技术：

近十多年来，我国高速列车技术发展迅猛，不仅服务于国内市场，更走向了世界。列车运营路线长而复杂，乘客上下车频繁，且列车提速是必然的趋势。因此，列车具备自动驾驶功能意义非常，研究列车自动驾驶控制技术具有明显的现实要求。

中国专利201110328206.3提供了一种列车自动驾驶系统实现站间运行自动驾驶曲线生成的方法，该方法通过实时获取列车自动监控系统的运营信息、列车参数信息、线路数据库的线路信息等，实时自适应计算列车站间各运行阶段的驾驶曲线信息，从而生成最优的列车站间运行自动驾驶曲线；该方法可有效保证列车的舒适性、安全性和节能等，但涉及实时采集大量信息，需要自动驾驶系统作大量的计算，当需要采集的信息过于密集时，实时性有待商榷。中国专利201310689453.5提供了一种自动驾驶的控制系统及方法，该方法设计了一个优化单元对多目标数据进行判断，结合反馈单元决策出优化的控制指令，实现列车的自适应自动驾驶控制；该控制系统可有效保证控制系统适应性、精确性，抑制列车性能的时间慢性漂移，但涉及使用模糊算法选用不同的控制器，从而得到不同的控制输出，这需要人为地作大量的规划从而得到模糊逻辑，一旦模糊逻辑选择不当，控制系统有失效的风险。

技术实现要素：

为解决上述问题，本发明提供一种基于elm的自动驾驶列车车速跟随的二阶变结构控制方法，通过以列车大量的任意站点区间历史运行数据为输入，利用elm算法进行神经网络训练获得列车自动驾驶模型，从而规划出任意站点间列车实时理想车速；利用astsm算法对列车车速进行控制，控制精度高、可有效抑制系统抖振，从而有效保证列车的安全性、舒适性和实时运行。

本发明提供一种基于elm的自动驾驶列车车速跟随的控制方法，包括以下步骤：

s1，以列车运行数据为输入，基于神经网络算法elm训练生成理想的列车自动驾驶模型，所述列车自动驾驶模型输出为列车车速；

s2，以所述s1生成的列车自动驾驶模型为理想模型，根据所述列车自动驾驶模型设计列车车速跟随控制器；

s3，对所述s2设计的列车车速跟随控制器进行稳定性分析，给出稳定条件；

s4，根据所述稳定条件设计列车牵引/制动力控制器。

较佳地，所述s1的具体过程为包括：

s1.1，采集某两站点之间人为驾驶列车的运行数据-实时加速度和距下一站点的距离数据，作为列车自动驾驶模型的训练输入；

s1.2，基于elm算法训练列车自动驾驶模型，包括确定训练集、激活函数和隐含节点个数，以及分配输入权重和阈值，具体为：

利用单隐含层反馈的elm算法训练获得列车自动驾驶模型；对于自动驾驭列车模型指定训练集：a为列车加速度，m/s²；；s为列车跟下一站点的距离，m；v为列车车速，km/h；激活函数为隐含节点数目选取为

单隐含层反馈的elm算法训练获得列车自动驾驶模型如下：

式中，wi＝[wi1,wi2]^t连接第i个隐含节点与输入节点的权重向量，即输入权重；βi连接第i个隐含节点与输出节点的权重向量，即输出权重；θi第i个隐含节点的阈值；wi·xj表示wi与xj的内积；输出节点选取为线性的；wi和θi均为随机分配；

若存在βi、wi和θi使下式成立：

那么，所述elm算法可使n个样本的训练集输入生成的列车自动驾驶模型接近零误差，即

s1.3，基于所述s1.2，计算隐含层输出矩阵h，具体为：

上式可写成下式的形式：

ηβ＝t

其中：

其中，h为神经网络隐含层输出矩阵，h的第i列对应输入x1,x2,...,xn的第i个隐含节点输出。

s1.4，基于所述s1.2和s1.3，计算输出权重并得到列车自动驾驶模型，具体为：

因隐含节点数与样本数存在关系：因此h不是方阵，为使模型训练有效，须使下式成立：

elm算法算计线性系统式的输出权重的最小范数最小二乘解如下式：

式中，是h的moore-penrose广义逆矩阵。

模型训练完成后，可得列车自动驾驶模型：

式中，为列车自动驾驶模型的输出-列车车速，km/h。

较佳地，所述s2的具体过程为：

s2.1，因elm算法训练生成的列车自动驾驶模型没有具体的动力学表达形式，故建立设计列车动力学模型如下：

式中，m为列车整备质量，kg；f为目标牵引力，n；d为行驶阻力与干扰的集总，n。；

s2.2，以所述s1训练获得的根据所述列车自动驾驶模型为理想模型，并基于stsm算法设计列车车速跟随控制器，具体如下：

定义滑模变量：

控制器输出为：

式中，α为控制增益；

假设：

式中，d1、d均为正常数；

s2.3，设计所述s2.2控制器增益的自适应律如下：

式中，ω、θ、υ、λ及αt均为正常数；

较佳地，所述s3的具体过程为：

s3.1，构造lyapunov函数：

其中：

v0(s)＝ζ^tpζ

式中，ε、α*均为正常数；

s3.2，证明v0(s)在有限时间内收敛：

由所述s3.1可知，矩阵p为正定矩阵，即有：v0(s)≥0；

对ζ求导可得：

其中：

对v0(s)求导：

当满足：

矩阵q为正定矩阵，

s3.3，证明v(s,α)在有限时间内收敛：

由所述s3.1和s3.2可知，v(s,α)≥0；

对v(s,α)求导并进行变形，如下：

利用不等式(a²+b²)/2≤|a|+|b|，得：

式中，

采用自适应律的控制增益α是有界的，这是因为，当0≤t≤tc时，有：

式中，tc为有限收敛时间，故控制增益α是有界的；而当时，增益α递减，直到重新满足；

由以上有界性分析可知，必存在一正数α^*，使得α-α^*＜0恒成立，因此有：

故系统目标函数可在有限时间内收敛到零点附近；因此，当满足：

所设计的控制器是稳定的。

较佳地，所述s4的具体过程为：

假设牵引力操纵杆的工作区间为：[0,ht]，设计牵引力操纵杆控制输出为：

式中，ft为列车可提供的最大牵引力；

假设制动力操纵杆的工作区间为：[0,hb]，设计制动力操纵杆控制输出为：

式中，fb为列车可提供的最大制动力，n。

本发明的积极进步效果在于：利用elm算法进行神经网络训练获得列车自动驾驶模型，从而规划出某站点间列车实时理想车速；在此基础上，基于astsm(二阶变结构算法-自适应超螺旋滑模)算法设计列车车速跟随控制器对列车车速进行控制。通过elm算法训练获得的列车自动驾驶模型可以高度模拟良好的列车驾驶行为，基于astsm算法设计的列车车速控制器，控制精度高、可有效抑制系统抖振，从而有效保证列车的安全性、舒适性和实时运行。

附图说明

图1是本发明一较佳实施例的基于elm的自动驾驶列车车速跟随的控制方法的列车自动驾驶模型的原理图；

图2是本发明一较佳实施例的基于elm的自动驾驶列车车速跟随的控制方法的列车牵引/制动力操纵杆控制器关系图；

图3是控制系统原理图。

具体实施方式

下面通过实施例的方式进一步说明本发明，但并不因此将本发明限制在所述的实施例范围之中。

基于elm的自动驾驶列车车速跟随的二阶变结构控制方法，如图1所示，包括以下步骤：

s1，以列车运行数据为输入，基于神经网络算法elm训练生成理想的列车自动驾驶模型，模型输出为列车车速；

s2，以所述s1生成的列车自动驾驶模型为理想模型，设计列车车速跟随控制器；

s3，对所述s2设计的列车车速跟随控制器进行稳定性分析，给出稳定条件；

s4，设计列车牵引/制动力控制器。

进一步，所述s1的具体过程为：

s1.1，采集某两站点之间人为驾驶列车的运行数据-实时加速度和距下一站点的距离数据，作为列车自动驾驶模型的训练输入；

s1.2，所述s1.1的elm算法，首先是确定训练集、激活函数和隐含节点个数，以及分配输入权重和阈值，具体为：

利用单隐含层反馈的elm算法训练获得列车自动驾驶模型。对于自动驾驭列车模型指定训练集：a为列车加速度，m/s²；s为列车跟下一站点的距离，m；v为列车车速，km/h；激活函数为隐含节点数目选取为n～。

式中，wi＝[wi1,wi2]^t连接第i个隐含节点与输入节点的权重向量，即输入权重；βi连接第i个隐含节点与输出节点的权重向量，即输出权重；θi第i个隐含节点的阈值；wi·xj表示wi与xj的内积；输出节点选取为线性的；wi和θi均为随机分配的。

若存在βi、wi和θi使式(2)成立：

那么，所述elm算法可使n个样本的训练集输入生成的列车自动驾驶模型接近零误差，即

s1.3，基于所述s1.2，计算隐含层输出矩阵h，具体为：

式(2)可写成式(3)的形式：

ηβ＝t(3)

其中：

其中，h为神经网络隐含层输出矩阵，h的第i列对应输入x1,x2,...,xn的第i个隐含节点输出。

s1.4，基于所述s1.2和s1.3，计算输出权重并得到列车自动驾驶模型，具体为：

因隐含节点数与样本数存在关系：因此h不是方阵，为使模型训练有效，须使式(6)成立：

elm算法算计线性系统式(3)的输出权重的最小范数最小二乘解如式(7)：

式中，是h的moore-penrose广义逆矩阵。

模型训练完成后，可得列车自动驾驶模型：

式中，为列车自动驾驶模型的输出-列车车速，km/h。

更进一步，所述s2的具体过程为：

s2.1，因elm算法训练生成的列车自动驾驶模型没有具体的动力学表达形式，故设计列车动力学模型如下：

式中，m为列车整备质量，kg；f为目标牵引力，n；d为行驶阻力与干扰的集总，n。

s2.2，以所述s1训练获得的列车自动驾驶模型为理想模型，基于stsm算法设计列车车速跟随控制器，具体如下：

定义滑模变量：

控制器输出为：

式中，α为控制增益。

假设：

式中，d1、d均为正常数。

滑模变量的一阶导及二阶导分别为：

s2.3，设计所述s2.2控制器增益的自适应律如下：

式中，ω、θ、υ、λ及αt均为正常数。

进一步，所述s3的具体过程为：

s3.1，构造lyapunov函数：

其中：

v0(s)＝ζ^tpζ(15)

式中，ε、α*均为正常数；

s3.2，首先证明v0(s)在有限时间内收敛：

由所述s3.1可知，矩阵p为正定矩阵，即有：v0(s)≥0；

对ζ求导可得：

其中：

对v0(s)求导：

当满足：

矩阵q为正定矩阵，

s3.3，再证明v(s,α)在有限时间内收敛：

由所述s3.1和s3.2可知，v(s,α)≥0。

对v(s,α)求导并进行变形，如下：

利用不等式(a²+b²)/2≤|a|+|b|，得：

式中，

采用自适应律的控制增益α是有界的，这是因为，当0≤t≤tc时，有：

式中，tc为有限收敛时间，故控制增益α是有界的；而当时，增益α递减，直到重新满足；

由以上有界性分析可知，必存在一正数α^*，使得α-α^*＜0恒成立，因此有：

故系统目标函数可在有限时间内收敛到零点附近；因此，当满足：

所设计的控制器是稳定的。证毕。所述基于astsm算法的列车车速跟随控制器与列车牵引/制动力操纵杆控制器关系如图2所示。

最后，所述s4的具体过程为：

假设牵引力操纵杆的工作区间为：[0,ht]，设计牵引力操纵杆控制输出为：

式中，ft为列车可提供的最大牵引力，n。

假设制动力操纵杆的工作区间为：[0,hb]，设计制动力操纵杆控制输出为：

式中，fb为列车可提供的最大制动力，n。

所述基于elm的自动驾驶列车车速跟随的二阶变结构控制方法设计的控制系统原理如图3所示。

虽然以上描述了本发明的具体实施方式，但是本领域的技术人员应当理解，这仅是举例说明，本发明的保护范围是由所附权利要求书限定的。本领域的技术人员在不背离本发明的原理和实质的前提下，可以对这些实施方式做出多种变更或修改，但这些变更和修改均落入本发明的保护范围。