一种倒立摆自适应迭代学习反演控制方法与流程

本发明涉及一种倒立摆自适应迭代学习反演控制方法，特别是带有未知输入饱和的倒立摆控制方法。

背景技术：

倒立摆系统的控制问题就是控制摆杆快速达到一个平衡位置，使其没有明显的振荡和过大的角度和速度。倒立摆系统具有自然不稳定性，强耦合，强非线性，存在外界干扰等特点，对倒立摆系统的研究可以有效反映非线性控制的典型问题，如非线性问题，鲁棒性问题等。因此研究存在输入饱和的情况下倒立摆系统的控制问题具有十分重要的意义。

迭代学习控制方法是一种具有强学习能力的控制方法，尤其是在解决重复作业的控制问题上展现了它的优越性。基于李雅普诺夫函数的自适应迭代学习控制充分利用上一次迭代后的系统信息，对系统的不确定参数和控制器中未知控制增益进行自适应迭代学习，不断提高系统的跟踪性能。针对系统参数或是结构存在非线性不确定性的情况下，自适应迭代学习控制能有效保证系统的稳定性，在有限时间区间内达到很高的跟踪精度。当系统模型不确定甚至是未知时，自适应迭代学习控制方法也可以达到完美的跟踪效果。

神经网络可以在任意精度内逼近一个未知函数，补偿不确定项，能有效地处理系统模型不确定性，参数不确定性等问题，因此被广泛用于解决系统动态模型中存在的不确定性。而径向基神经网络结构具有三层前馈网络，结构简单，收敛快速，不仅优化了算法的学习速度又避免了局部极小问题。

在研究非线性系统控制问题时，大多数的增益函数都是未知的，在李雅普诺夫稳定性分析中会有可能会出现由于对系统未知增益函数的求导而引起的奇异值问题等控制问题，因此构造一个简单有效的李雅普诺夫函数十分重要。因此，研究在存在输入饱和情况下，利用神经网络和反演控制方法，结合自适应迭代学习，实现倒立摆系统的高精度跟踪控制具有很高的理论和实际意义。

技术实现要素：

为了克服现有倒立摆存在的未知输入饱和问题，本发明提供一种倒立摆自适应迭代学习反演控制方法，在系统存在输入饱和的情况下，估计和补偿系统未知不确定性，解决由未知增益函数求导引起的控制问题，实现在有限迭代次数内系统跟踪误差二范数收敛到零附近的控制方法。

为了解决上述技术问题提出的技术方案如下：

一种倒立摆自适应迭代学习反演控制方法，所述控制方法包括以下步骤：

步骤1，建立倒立摆的动态模型，初始化系统状态、采样时间以及控制参数，过程如下：

1.1倒立摆的动态模型表达形式为：

其中x1,k，x2,k分别是角度位置和角速度，k是迭代次数；分别是角度位置和角速度的一阶导数；g是重力加速度；mc，m是分别是小车和倒立摆的质量；l是倒立摆长度的一半；uk表示控制输入，sat(uk)表示受饱和限制的控制输入，其表达形式为：

其中um是uk的最大值，|uk|表示uk的绝对值，sgn(uk)表示uk的符号函数；

1.2定义未知函数f(xk)和b(xk)，将式(1)写成以下形式：

其中是未知的光滑函数；xk＝[x1,k,x2,k]^t；从b(xk)的表达式中得到b(xk)＞0；

步骤2，逼近和估计输入饱和项，其过程如下：

采用以下的双曲正切函数逼近输入饱和函数：

其中tanh(·)表示双曲正切函数；

由此得

sat(uk)＝g(uk)+d(uk)(5)

其中d(uk)是一个有界函数，满足

|d(uk)|＝|sat(uk)-g(uk)|≤um(1-tanh(1))＝d(6)

其中d是一个未知正数，|d(uk)|表示d(uk)的绝对值；

通过微分中值定理计算，得出

其中uξ＝ξuk+(1-ξ)u0，u0∈[0,uk]；0＜ξ＜1是一个常数；是uk＝uξ时对g(uk)的偏导，取u0＝0，g(u0)＝0；则公式(7)写为：

将公式(8)代入到公式(5)中，得

步骤3，计算系统跟踪误差，其过程如下：

定义系统跟踪误差z1,k如下：

z1,k＝x1,k-xd(10)

其中xd是给定的光滑有界的参考轨迹；

对公式(10)求导得到：

其中是系统跟踪误差的一阶导数，是参考轨迹的一阶导数；

步骤4，定义误差变量，设计虚拟控制器，其过程如下：

4.1定义误差变量z2,k为：

z2,k＝x2,k-α1,k(12)

其中，α1,k是设计控制器过程中的虚拟控制器；系统初始条件为：z1,k(0)＝0，z2,k(0)＝0；

对式(12)进行求导，得到：

其中是误差变量的一阶导数，是设计控制器过程中虚拟控制器的一阶导数；

将式(3)，式(9)代入式(11)和式(13)中，得到：

由此，计算：

其中

由于0＜guξ≤1，则必定存在一个正的常数gn使得成立；然后，得出是有界的，并且

其中表示的绝对值，ρd是一个大于零的常数；

4.2为逼近函数设计以下神经网络：

定义w^*为神经网络理想权重矩阵，则写成以下形式：

其中w^*t＝w^*，是神经网络的输入向量，是参考轨迹的二次导数，εk是神经网络的逼近误差且满足|εk|≤σn，|εk|表示εk的绝对值，σn是|εk|的上界，是一个正的常数，φ(xk)＝[φ1(xk),φ2(xk),…,φm(xk)]^t是神经网络的基函数，m为神经元的个数，φi(xk)的形式如下所示：

其中ιi和υi分别是高斯函数的中心和宽度，i＝1,…,m，其中exp(·)是指数函数；

4.3设计神经网络权值和估计误差更新律：

其中γ1，γ2，β1，β2都是合适的参数，分别表示在第k和k-1次迭代时对w^*和σn的估计，是和的一阶导数，δ是一个正的常数；给定

4.4设计虚拟控制器和实际控制器，如下：

其中c1，c2是正常数，

4.5把式(18)，式(22)和式(23)代入到式(15)和式(16)中，得：

其中

步骤5，构造李雅普诺夫函数vk(t)与类李雅普诺夫函数ek(t)，分析系统性能，其过程如下所示：

其中

对vk(t)求导，并将式(24)，(25)代入，得到：

其中和分别是和的一阶导数；

将(17)代入(28)，得到：

其中|z2,k|表示z2,k的绝对值；

然后，写为：

其中

将(20)，(21)代入(30)，得：

采用双曲正切函数的以下性质：

0≤|z2,k|-z2,ktanh(z2,k/δ)≤0.2785δ；(32)

将式(32)代入(31)，得到：

对式(27)求导，得到：

在初始迭代k＝0时，和则由此得到：

对式(35)两侧同时进行积分运算，得到：

可以看出在[0,t]中是有界的；在初始条件的选择下，v0(0)也是有界的；得出e0(t)是有界的，即

ek(t)在第k次迭代的差分形式为：

其中vk-1(t)和ek-1(t)分别是第k-1次的李雅普诺夫函数和类李雅普诺夫函数；

将式(33)代入(38)中，得到

结合得到：

其中t表示倒立摆系统的迭代周期；cm＝min{c1,c2}表示取c1，c2的最小值；表示一个正的常数；zr,k，r＝1,2表示误差变量；

对δek(t)有限迭代次数的累加得到：

其中ek(t)表示第k次迭代，t＝t时的类李雅普诺夫函数；e0(t)表示k-1，t＝t时的类李雅普诺夫函数；

将(40)代入到(41)，写成：

从(42)得出：

其中表示zr,k，r＝1,2的二范数形式；

则判定对于任意给定常数都存在一个正的有限迭代次数k0，对于k＞k0，使得成立；也就是说，系统跟踪误差z1,k在二范数的意义上在有限迭代次数内收敛到零附近的领域内。

本发明基于含有未知输入饱和问题的倒立摆系统模型，结合反演控制算法，神经网络，自适应迭代学习控制方法，设计了倒立摆自适应迭代学习反演控制方法，解决了系统中输入饱和问题，解决由未知增益函数求导引起的控制问题，实现在有限迭代次数内系统跟踪误差二范数收敛到零附近的。

本发明的技术构思为：针对含有未知输入饱和的倒立摆，设计自适应迭代学习控制，基于微分中值定理，通过光滑的双曲正切函数拟合饱和函数，然后，利用神经网络逼近系统中的不确定项，设计一种倒立摆自适应迭代学习反演控制方法。本发明提供了一种能补偿系统未知不确定项，解决由未知增益函数求导引起的控制问题，实现在有限迭代次数内系统跟踪误差二范数收敛到零附近的控制方法。

本发明的有益效果为：补偿系统未知不确定项，解决了由未知增益函数求导引起的控制问题，实现在有限迭代次数内系统跟踪误差二范数收敛到零附近。

附图说明

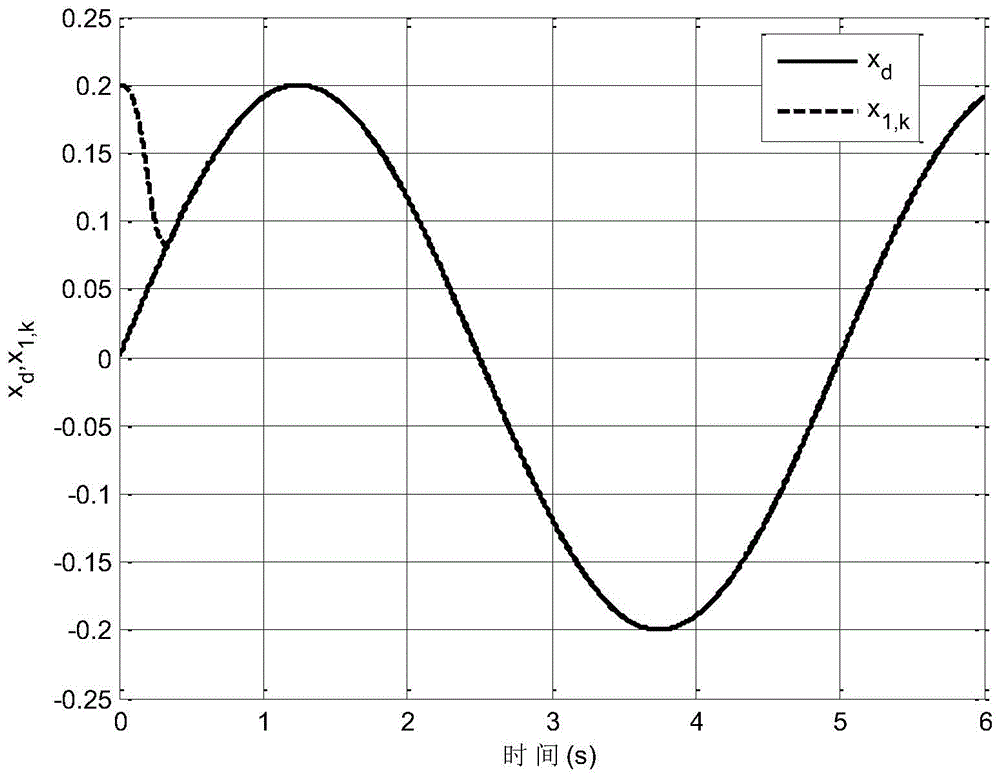
图1为本发明的跟踪效果图；

图2为本发明的跟踪误差图；

图3为本发明的控制输入图；

图4为本发明的系统性能指标图；

图5为本发明的控制流程示意图。

具体实施方式

下面结合附图对本发明做进一步说明。

参照图1-图5，一种倒立摆自适应迭代学习反演控制方法，其特征在于：所述控制方法包括以下步骤：

步骤1，建立倒立摆的动态模型，初始化系统状态、采样时间以及控制参数，过程如下：

1.1倒立摆的动态模型表达形式为：

其中x1,k，x2,k分别是角度位置和角速度，k是迭代次数；分别是角度位置和角速度的一阶导数；g是重力加速度；mc，m是分别是小车和倒立摆的质量；l是倒立摆长度的一半；uk表示控制输入，sat(uk)表示受饱和限制的控制输入，其表达形式为：

其中um是uk的最大值，|uk|表示uk的绝对值，sgn(uk)表示uk的符号函数；

1.2定义未知函数f(xk)和b(xk)，将式(1)写成以下形式：

其中是未知的光滑函数；xk＝[x1,k,x2,k]^t；从b(xk)的表达式中得到b(xk)＞0；

步骤2，逼近和估计输入饱和项，其过程如下：

采用以下的双曲正切函数逼近输入饱和函数：

其中tanh(·)表示双曲正切函数；

由此得

sat(uk)＝g(uk)+d(uk)(5)

其中d(uk)是一个有界函数，满足

|d(uk)|＝|sat(uk)-g(uk)|≤um(1-tanh(1))＝d(6)

其中d是一个未知正数，|d(uk)|表示d(uk)的绝对值；

通过微分中值定理计算，得出

其中uξ＝ξuk+(1-ξ)u0，u0∈[0,uk]；0＜ξ＜1是一个常数；是uk＝uξ时对g(uk)的偏导，取u0＝0，g(u0)＝0；则公式(7)写为：

将公式(8)代入到公式(5)中，得

步骤3，计算系统跟踪误差，其过程如下：

定义系统跟踪误差z1,k如下：

z1,k＝x1,k-xd(10)

其中xd是给定的光滑有界的参考轨迹；

对公式(10)求导得到：

其中是系统跟踪误差的一阶导数，是参考轨迹的一阶导数；

步骤4，定义误差变量，设计虚拟控制器，其过程如下：

4.1定义误差变量z2,k为：

z2,k＝x2,k-α1,k(12)

其中，α1,k是设计控制器过程中的虚拟控制器；系统初始条件为：z1,k(0)＝0，z2,k(0)＝0；

对式(12)进行求导，得到：

其中是误差变量的一阶导数，是设计控制器过程中虚拟控制器的一阶导数；

将式(3)，式(9)代入式(11)和式(13)中，得到：

由此，计算：

其中

由于0＜guξ≤1，则必定存在一个正的常数gn使得成立；然后，得出是有界的，并且

其中表示的绝对值，ρd是一个大于零的常数；

4.2为逼近函数设计以下神经网络：

定义w^*为神经网络理想权重矩阵，则写成以下形式：

其中w^*t＝w^*，是神经网络的输入向量，是参考轨迹的二次导数，εk是神经网络的逼近误差且满足|εk|≤σn，|εk|表示εk的绝对值，σn是|εk|的上界，是一个正的常数，φ(xk)＝[φ1(xk),φ2(xk),…,φm(xk)]^t是神经网络的基函数，m为神经元的个数，φi(xk)的形式如下所示：

其中ιi和υi分别是高斯函数的中心和宽度，i＝1,…,m，其中exp(·)是指数函数；

4.3设计神经网络权值和估计误差更新律：

其中γ1，γ2，β1，β2都是合适的参数，分别表示在第k和k-1次迭代时对w^*和σn的估计，是和的一阶导数，δ是一个正的常数；给定

4.4设计虚拟控制器和实际控制器，如下所示：

其中c1，c2是正常数，

4.5把式(18)，式(22)和式(23)代入到式(15)和式(16)中，得：

其中

步骤5，构造李雅普诺夫函数vk(t)与类李雅普诺夫函数ek(t)，分析系统性能，其过程如下所示：

其中

对vk(t)求导，并将式(24)，(25)代入，得到：

其中和分别是和的一阶导数；

将(17)代入(28)，得到：

其中|z2,k|表示z2,k的绝对值；

然后，写为：

其中

将(20)，(21)代入(30)，得：

采用双曲正切函数的以下性质：

0≤|z2,k|-z2,ktanh(z2,k/δ)≤0.2785δ；(32)

将式(32)代入(31)，得到：

对式(27)求导，得到：

在初始迭代k＝0时，和则由此得到：

对式(35)两侧同时进行积分运算，得到：

可以看出在[0,t]中是有界的；在初始条件的选择下，v0(0)也是有界的；得出e0(t)是有界的，即

ek(t)在第k次迭代的差分形式为：

其中vk-1(t)和ek-1(t)分别是第k-1次的李雅普诺夫函数和类李雅普诺夫函数；

将式(33)代入(38)中，得到

结合得到：

其中t表示倒立摆系统的迭代周期；cm＝min{c1,c2}表示取c1，c2的最小值；表示一个正的常数；zr,k，r＝1,2表示误差变量；

对δek(t)有限迭代次数的累加得到：

其中ek(t)表示第k次迭代，t＝t时的类李雅普诺夫函数；e0(t)表示k-1，t＝t时的类李雅普诺夫函数；

将(40)代入到(41)，写成：

从(42)得出：

其中表示zr,k，r＝1,2的二范数形式；

则判定对于任意给定常数都存在一个正的有限迭代次数k0，对于k＞k0，使得成立；也就是说，系统跟踪误差z1,k在二范数的意义上在有限迭代次数内收敛到零附近的领域内。

为了验证所提方法的有效性，本方法针对倒立摆模型进行仿真验证。倒立摆系统参数设置如下：mc＝1kg，m＝0.1kg，l＝0.5m，g＝9.8m/s²，um＝5.5n·m；系统初始化参数设置如下：神经网络的神经元个数如下：n＝150，对高斯函数的宽度设定如下：υj＝3，j＝1,…,n，其中心ιj，j＝1,…,n均匀分布在[-0.5,0.5]×[-0.5,0.5]×[-0.5,0.5]×[-0.5,0.5]×[-0.5,0.5]中，神经网络权值以及误差估计的更新律参数如下：γ1＝0.7，γ2＝0.8，β1＝2，β2＝2，虚拟控制器和实际控制器的系数如下：c1＝6，c2＝25，δ＝0.5，系统初始值给定：x1,k(0)＝0.2，x2,k(0)＝0，参考轨迹方程为：xd(t)＝0.2sin(0.4πt)，修正后的参考轨迹方程如下：

其中设定时间δ＝0.4s，周期时间t＝6s，xr(t)＝a5t⁵+a4t⁴+a3t³+a2t²+a1t+a0，

a0＝x1,k(0)

其中xd(δ)，是在设定时间上的期望轨迹的值和它的一阶导数和二阶导数；x1,k(0)，是在初始时刻倒立摆系统的角度位置的值和它的一阶导数和二阶导数；

图1和图2表示的分别是系统角度位置跟踪效果和对应的跟踪误差，可以看出系统的角度位置x1,k可以很好地跟踪参考轨迹xd，并且保证跟踪误差收敛在一个邻域内；图3表示了系统的控制输入；图4表示系统的性能指标。

因此，本发明能提供一种可以补偿系统未知不确定项，并解决由未知增益函数求导引起的控制问题的自适应迭代学习控制方法，实现了在有限迭代次数内系统跟踪误差二范数收敛到零附近。

以上阐述的是本发明给出的一个实施例表现出的优良优化效果，显然本发明不只是限于上述实施例，在不偏离本发明基本精神及不超出本发明实质内容所涉及范围的前提下对其可作种种变形加以实施。