一种6-3-PUS并联机构的轨迹跟踪控制方法及装置

一种6-3-pus并联机构的轨迹跟踪控制方法及装置
技术领域
1.本技术涉及运动控制和机器人学技术领域，尤其涉及一种6-3-pus并联机构的轨迹跟踪控制方法及装置。


背景技术：

2.6-3-pus并联机构是一种六自由度的并联机器人，由静平台、动平台和六条支链组成。不同于常见的六自由度并联机构，如stewart平台，6-3-pus并联机构的分支驱动器安装在静平台，减少了对支链运动的限制，具有更大的工作空间和更强的动态性能，使其在生产加工和运动测试等方面有着广阔的应用前景。轨迹跟踪控制的目标是改变驱动力矩，使得并联机构按照期望轨迹运动，常用的基于运动学模型的反馈控制算法，虽然计算简单，但其迭代修正误差的策略，导致了控制的滞后性。此外，控制反馈所需的并联机构动平台的实际位姿，往往需要精确的测量系统获得，这无疑给反馈运动控制增加了限制。


技术实现要素：

3.本技术实施例的目的是提供一种6-3-pus并联机构的轨迹跟踪控制方法及装置，以解决相关技术中存在的6-3-pus并联机构轨迹跟踪的控制精度不足，且控制过程不受位姿测量系统的限制的技术问题。
4.根据本技术实施例的第一方面，提供一种6-3-pus并联机构的轨迹跟踪控制方法，包括：
5.建立6-3-pus并联机构的运动学模型和动力学模型；
6.选取状态变量，将所述动力学模型转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力；
7.将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，其中ρ和用作lqr控制器的反馈。
8.进一步地，建立6-3-pus并联机构的运动学模型，包括：
9.建立6-3-pus并联机构的反向运动学模型；
10.根据所述反向运动学模型，运用牛顿迭代法，根据输入的关节坐标q计算出动平台的位姿t；
11.设计6-3-pus并联机构的正向运动学的解析方法，建立关节坐标的时间微分和运动坐标的时间微分的解析关系。
12.进一步地，建立6-3-pus并联机构的动力学模型，包括：
13.在6-3-pus并联机构的运动空间中，建立运动坐标ρ及其微分与运动空间的力f之
间的等效关系，即6-3-pus并联机构的动力学模型。
14.进一步地，选取状态变量，将所述动力学方程转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力，包括：
15.以运动坐标ρ为控制变量，选取状态变量观测变量y＝x，所述lqr控制器的状态空间方程为：
[0016][0017]
y＝x
[0018]
其中所述控制器的输入为e＝y
d-y，其中yd为期望值y为实际值；所述控制器的输出为运动空间的力f＝u+g
ρ
，与控制器的控制率u有关，通过求解最小化线性二次型性能指标问题：获得控制率u。
[0019]
进一步地，将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，包括：
[0020]
获取运动空间的力f和关节的驱动力矩τ的映射关系τ＝j
t
f，其中j为关节速度和运动坐标之间的解析雅可比矩阵；
[0021]
根据6-3-pus并联机构输出的关节的实际坐标q和实际速度通过约束方程求解，求得实际的运动坐标ρ，通过正向运动学的解析方法，求得实际的运动坐标的时间微分ρ和作为控制反馈，计算误差。
[0022]
根据本技术实施例的第二方面，提供一种6-3-pus并联机构的轨迹跟踪控制装置，包括：
[0023]
建模模块，用于建立6-3-pus并联机构的运动学模型和动力学模型；
[0024]
设计控制器模块，用于选取状态变量，将所述动力学模型转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力；
[0025]
求解模块，将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，其中ρ和用作lqr控制器的反馈。
[0026]
根据本技术实施例的第三方面，提供一种电子设备，包括：
[0027]
一个或多个处理器；
[0028]
存储器，用于存储一个或多个程序；
[0029]
当所述一个或多个程序被所述一个或多个处理器执行，使得所述一个或多个处理器实现如第一方面所述的方法。
[0030]
根据本技术实施例的第四方面，提供一种计算机可读存储介质，其上存储有计算机指令，该指令被处理器执行时实现如第一方面所述方法的步骤。
[0031]
本技术的实施例提供的技术方案可以包括以下有益效果：
[0032]
由上述实施例可知，本技术因为进行了6-3-pus并联机构的动力学分析，控制考虑了动平台和关节的动态力矩情况，相比基于运动学分析的控制方法，提高了控制精度；因为能及时输入合适的驱动力矩，降低了系统能耗；因为采用了lqr控制器，降低了对控制增益参数的依赖。
[0033]
应当理解的是，以上的一般描述和后文的细节描述仅是示例性和解释性的，并不能限制本技术。
附图说明
[0034]
此处的附图被并入说明书中并构成本说明书的一部分，示出了符合本技术的实施例，并与说明书一起用于解释本技术的原理。
[0035]
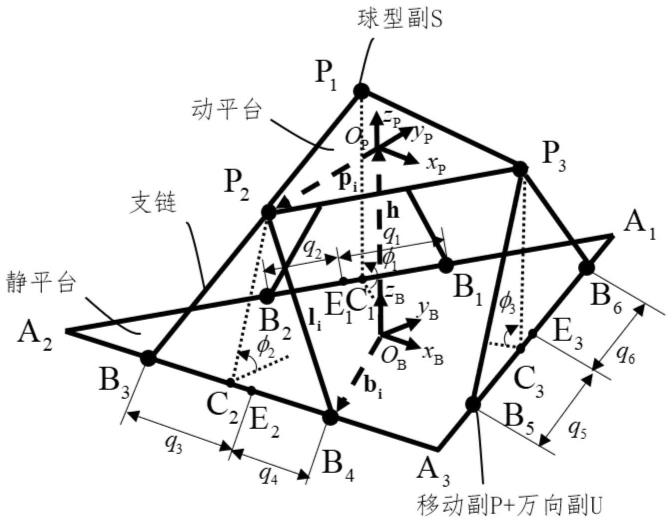
图1是根据一示例性实施例示出的6-3-pus并联机构的结构简图。
[0036]
图2是根据一示例性实施例示出的一种6-3-pus并联机构的轨迹跟踪控制方法的流程图。
[0037]
图3是根据一示例性实施例示出的6-3-pus并联机构的正向运动学数值解法的流程图。
[0038]
图4是根据一示例性实施例示出的基于lqr控制的6-3-pus并联机构的控制结构图。
[0039]
图5是根据一示例性实施例示出的一种6-3-pus并联机构的轨迹跟踪控制装置的框图。
具体实施方式
[0040]
这里将详细地对示例性实施例进行说明，其示例表示在附图中。下面的描述涉及附图时，除非另有表示，不同附图中的相同数字表示相同或相似的要素。以下示例性实施例中所描述的实施方式并不代表与本技术相一致的所有实施方式。相反，它们仅是与如所附权利要求书中所详述的、本技术的一些方面相一致的装置和方法的例子。
[0041]
在本技术使用的术语是仅仅出于描述特定实施例的目的，而非旨在限制本技术。在本技术和所附权利要求书中所使用的单数形式的“一种”、“所述”和“该”也旨在包括多数形式，除非上下文清楚地表示其他含义。还应当理解，本文中使用的术语“和/或”是指并包含一个或多个相关联的列出项目的任何或所有可能组合。
[0042]
6-3-pus并联机构是一种六自由度的并联机器人，其命名中的6和3分别表示支链在静平台和动平台上的连接点数，p、u、s分别表示三种运动副(连接两个机械构件并约束其相对运动的元件)：移动副、万向副、球型副，整体结构的连接顺序从下到上依次为：静平台-移动副p-万向副u-球型副s-动平台。不同于常见的六自由度并联机构，pus并联机构是通过改变支链与静平台铰点的位置来实现动平台的运动，而支链长度保持不变。这种结构设计
使得驱动器不再安装在支链上，减少对支链运动的阻碍，提高动态性能，便于增大工作空间；且驱动器执行需要克服的阻力减小，对电机的驱动力矩要求降低，有利于提高驱动力矩有效利用率。
[0043]
为了使后续的方法描述更加清晰，这里对方法描述中涉及的变量和符号作如下解释。图1是根据一示例性实施例示出的6-3-pus并联机构的结构简图，如图1所示，6-3-pus并联机构由静平台(正δa1a2a3)、动平台(正δp1p2p3)和三对支链b
2k-1
pk、b
2k
pk(k＝1,2,3)组成，δa1a2a3和δp1p2p3的边长分别为la和lp，lp＝la/2，支链长度为固定值l。{o
p
}、{ob}分别为动平台和静平台上的坐标系，坐标系原点都位于各自正三角形的中心位置。pk为支链与动平台的上铰点，静平台一侧的两条支链的上铰点重合，pk相对动平台坐标系{o
p
}的位置不变，b
2k-1
和b
2k
是一侧的两条支链与静平台的下铰点，下铰点可以沿着静平台δa1a2a3的边缘移动。δa1a2a3三条边的中点为ek(k＝1,2,3)，ek到b
2k-1
和b
2k
的距离分别为q
2k-1
和q
2k
，这是控制并联机构运动的输入变量，也是关节空间坐标，q＝[q1,q2,q3,q4,q5,q6]
t
。φi表示等腰δb
2k-1
p
kb2k
(k＝1,2,3)所在平面与静平台所在平面的夹角，φ＝[φ1,φ2,φ3]
t
，φ与q有关。定义运动空间坐标在实际控制中，还需要将q转化为驱动器的控制变量，即驱动电机的输入力矩τ。
[0044]
轨迹跟踪控制的目标是输入最合适的驱动变量，使得并联机构按照预定轨迹执行运动。常见的控制方法是基于运动学模型，输入目标位移或速度进行反馈控制，但这种方法因为缺少对动态驱动力矩的观测，只能通过反馈调节来使实际输出逼近目标值，所以存在明显的控制延时，且控制性能非常依赖于增益参数，这对系统设计造成不便。对于并联机构这样的非线性系统，更精准快速的控制还需要建立动力学模型，能及时根据系统的状态需要调整控制输入，减小控制响应时间，提高控制精度。
[0045]
图2是根据一示例性实施例示出的一种6-3-pus并联机构的轨迹跟踪控制方法的流程图，如图2所示，该方法应用于6-3-pus并联机构中，可以包括以下步骤：
[0046]
步骤s11：建立6-3-pus并联机构的运动学模型和动力学模型；
[0047]
步骤s12：选取状态变量，将所述动力学模型转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力；
[0048]
步骤s13：将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，其中ρ和用作lqr控制器的反馈。
[0049]
由上述实施例可知，本技术因为进行了6-3-pus并联机构的动力学分析，控制考虑了动平台和关节的动态力矩情况，相比基于运动学分析的控制方法，提高了控制精度；因为能及时输入合适的驱动力矩，降低了系统能耗；因为采用了lqr控制器，降低了对控制增益参数的依赖。
[0050]
在步骤s11的具体实施中，建立6-3-pus并联机构的运动学模型和动力学模型；
[0051]
具体地，通过运用了正运动学求解方法(数值方法和解析方法)，将方便观测的关
节坐标和速度转化为动平台的位姿和速度，不需要精确位姿测量系统，就能获得实际的动平台位姿和速度，克服了位姿测量的限制，建立6-3-pus并联机构的运动学模型的过程可以包括：
[0052]
步骤s21：建立6-3-pus并联机构的反向运动学模型；
[0053]
具体地，对于已知的某个动平台位姿，又称运动空间坐标，用于描述动平台的位置和姿态，定义为t＝[t
x
,ty,tz,α,β,γ]
t
。t在静平台坐标系{ob}中可以通过平移向量h和旋转矩阵r表示，其中平移向量h用x,y,z三个轴的平移量t
x
,ty,tz表示：h＝[t
x
,ty,tz]
t
，旋转矩阵r用绕x,y,z三个轴旋转的欧拉角α,β,γ表示：
[0054][0055]
如图1所示，在静平台坐标系{ob}中存在如下的空间向量关系：
[0056]
rpi+h-bi＝l
i (i＝1,...,6)
ꢀꢀꢀ
(1)
[0057]
pi为上铰点在坐标系{o
p
}中的位置向量，bi为下铰点bi在坐标系{ob}中的位置向量，li为支链在坐标系{ob}中的位置向量。由于bi沿着δa1a2a3的边移动，因此向量bi的x坐标和y坐标存在线性约束，向量bi可以表示为：
[0058]bi
＝[x
i μixi+v
i 0]
t
ꢀꢀꢀ
(2)
[0059]
其中xi为下铰点bi的x坐标，μi和vi为下铰点bi的x坐标与y坐标之间的线性约束系数，在pus并联机构中，支链li长度保持不变，为l，因此可以将公式(2)代入公式(1)，并同时对公式(1)等号两边平方，获得关于xi的一元二次方程，共得到三个方程，对其进行求解，在方程有实根的情况下，每个方程的两个实根均是有效的，分别表示静平台一侧的两个下铰点的x坐标。由xi进一步根据正三角形的几何关系获得关节坐标变量qi的值，由此计算出关节坐标q。进一步地，由并联机构存在的几何关系，可以得到关节坐标输入q和角度φ的几何约束方程r(q,φ)＝0，其中包含三个方程，对于已知的q，求解φ，并根据实际的并联机构状态，获得符合的唯一解，由此获得运动坐标ρ，并进一步微分得到完成反向运动学模型的搭建。建立基本的反向运动学模型，明确平台位姿到运动坐标的计算过程，为后续的正向运动学分析、动力学分析和轨迹跟踪控制奠定理论基础。
[0060]
步骤s22：设计6-3-pus并联机构的正向运动学的数值方法，根据所述反向运动学模型，运用牛顿迭代法，根据输入的关节坐标q计算出动平台的位姿t；
[0061]
具体地，将步骤s21描述的反向运动学过程定义为qi＝gi(t
x
,ty,tz,α,β,γ)，已知关节坐标变量动平台位姿参数和关节坐标变量之间的约束方程为
[0062][0063]
记误差f＝[f1,f2,f3,f4,f5,f6]
t
，正向运动学的目标是根据给定的关节坐标变量q0，计算动平台位姿t＝[t
x
,ty,tz,α,β,γ]
t
，使得f＝0，本发明采用牛顿迭代法进行求解，求解过程如图3所示，由以下步骤构成：
[0064]
s31：选取初始位姿k表示迭代周期，设定极小正值ε1和ε2，用于判断迭代是否终止；
[0065]
s32：代入位姿约束方程(3)，计算误差f(t
(k)
)；
[0066]
s33：如果‖f(t
(k)
)‖＜ε1，迭代结束，t
(k)
即为所求的动平台位姿，否则，进行下一步；
[0067]
s34：计算f关于位姿t
(k)
的偏导数
[0068]
s35：由j(t
(k)
)δt＝-f(t
(k)
)计算位姿修正值δt；
[0069]
s36：如果‖δt‖＜ε2，迭代结束，t
(k)
即为所求的动平台位姿，否则，更新位姿t
(k+1)
＝t
(k)
+δt，更新迭代次数k＝k+1，回到步骤s32。
[0070]
由上述过程，选定一个合适的初值，在缺少精密的位姿测量仪器时，可以根据驱动电机的编码器反馈值得到实际的关节坐标变量，再通过正向运动学的数值方法，获得动平台的实际位姿。通过牛顿迭代法求解正向运动学，能够简单快捷地获得实际位姿，方便对动平台运动状态的观测。
[0071]
步骤s23：设计6-3-pus并联机构的正向运动学的解析方法，建立关节坐标的时间微分和运动坐标的时间微分的解析关系。
[0072]
具体地，由并联机构存在的几何关系，可以得到关节坐标输入q和角度φ的几何约束方程r(q,φ)＝0，包含三个方程，对于已知的q，求解φ，并根据实际的并联机构状态，获得符合的唯一解。对运动约束r(q,φ)＝0，进行时间微分，得到：
[0073][0074]
可得为：
[0075][0076]
将公式(5)代入可得
[0077][0078]
即关节坐标的时间微分和运动坐标的时间微分存在如下解析关系：
[0079][0080]
其中j为解析雅可比矩阵：
[0081][0082]
由此完成了正向运动学的解析方法的描述，对于关节坐标的时间微分可以通过公式(7)求得运动坐标的时间微分通过以上的正向运动学的解析方法，可以从几何上确
定关节坐标和运动坐标在时间微分上的转换关系，便于在运动控制中进行反馈计算。
[0083]
具体地，建立6-3-pus并联机构的动力学模型的过程可以包括：
[0084]
在6-3-pus并联机构的运动空间中，建立运动坐标ρ及其微分与运动空间的力f之间的等效关系，即6-3-pus并联机构的动力学模型。
[0085]
具体地，6-3-pus并联机构的动力学模型主要由运动关节的动力学模型和动平台的动力学模型组成，可以通过拉格朗日方程推导。在运动空间中，6-3-pus并联机构关于运动坐标ρ的整体动力学方程如下：
[0086][0087]
其中，m
ρ
为并联机构整体的惯性矩阵，c
ρ
为科里奥利力和离心力矩阵，g
ρ
为重力向量，f为运动空间的力。通过动力学模型能够获得并联机构在运动过程中所需的驱动力，从而在运动过程中输入更合适的力矩，降低控制功耗，减少机械设备损伤。
[0088]
在步骤s12的具体实施中，选取状态变量，将所述动力学模型转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力；
[0089]
具体地，以运动坐标ρ为控制变量，为了应用lqr(linear quadratic regulator，线性二次型调节器)控制方法，需要将6-3-pus并联机构的动力学方程转换为线性的状态空间方程。考虑如下的线性系统的状态空间方程：
[0090][0091]
选取状态变量观测变量y＝x，结合公式(10)，状态空间方程转化为：
[0092][0093]
由公式(10)和(11)对照可见：
[0094][0095]
在轨迹跟踪任务中，lqr控制器的控制目标不是使状态变量x趋向于零，而是使得观测误差e＝y
d-y趋向于零，其中yd为期望变量包括动平台的期望位姿和期望速度。因此，控制目标是寻找一个控制率u，使得线性二次型性能指标j最小，j的计算公式为：
[0096][0097]
其中，q是状态约束矩阵，r是控制约束矩阵，都是对角矩阵，用最优化的思想选择q
和r的值，以达到响应速度和系统能耗之间的平衡。
[0098]
控制率u＝kcx+kgyd中，kc＝-r-1bt
p，其中，p为代数riccati方程pa+a
t
p-pbr-1bt
p+c
t
qc＝0的解，kg＝r-1bt
(pbr-1bt-a
t
)c
t
q，
[0099]
转化为控制器的输出，即运动空间的力为：
[0100]
f＝u+g
ρ
＝kcx+kgyd+g
ρ
ꢀꢀꢀ
(14)
[0101]
利用lqr原理和动力学模型建立控制器，既有效利用了动力学分析的优点，也降低了控制增益参数的约束影响，从而提高6-3-pus并联机构的运动控制精度。
[0102]
在步骤s13的具体实施中，将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，其中ρ和用作lqr控制器的反馈；
[0103]
具体地，此步骤可以包括以下子步骤：
[0104]
步骤s41：获取运动空间的力f和关节的驱动力矩τ的映射关系τ＝j
t
f，其中j为关节速度和运动坐标之间的解析雅可比矩阵；
[0105]
具体地，在实际控制中，6-3-pus并联机构的控制力矩不是运动空间的力f，而是关节空间的控制力矩τ，因此需要实现力分布，将运动空间的力矩f映射到各个关节上。
[0106]
由虚功定理可以得知，所有驱动器和外力做的虚功δw为零，即：
[0107]
δw＝τ
t
δq-f
t
δρ＝0
ꢀꢀꢀ
(15)
[0108]
虚位移δq可以等效为q关于时间的微分δρ可以等效为ρ关于时间的微分因此虚位移δq和δρ能通过公式(7)定义的解析雅可比矩阵关联：δρ＝jδq，代入公式(15)，得(τ
tjt-f
t
)δρ＝0，这对任意虚拟位移δρ成立，因此τ
tjt-f
t
＝0，可得：
[0109]
τ＝j
tfꢀꢀꢀ
(16)
[0110]
这一步骤将力矩信息从运动空间转化到关节空间，从而控制并联机构执行有效的运动。
[0111]
步骤s42：根据6-3-pus并联机构输出的关节的实际坐标q和实际速度通过约束方程求解，求得实际的运动坐标ρ，通过正向运动学的解析方法，求得实际的运动坐标的时间微分ρ和作为控制反馈，计算误差。
[0112]
具体地，由运动空间的力f和关节的驱动力矩τ的映射关系可以将运动空间的力f转化为关节的驱动力矩τ。图4是根据一示例性实施例示出的6-3-pus并联机构的轨迹跟踪控制结构图，对于动平台的期望位姿td，进行反向运动学求解，获得期望的运动坐标ρd及其时间微分设计步骤s13所述的lqr控制器，控制器输入为运动坐标误差和运动坐标时间微分的误差，控制器输出为运动空间的力f，也就是动平台受到的力；经过步骤s41所述的映射关系(15)，将运动空间的力f映射到关节空间的力矩τ，驱动6-3-pus并联机构执行运动；并联机构的输出变量为关节空间的坐标q和速度通过步骤s11所述的约束方程求解方法和正向运动学解析关系，分别求得运动空间实际的坐标ρ及其时间微分两者作为控制反馈，计算误差。通过步骤s11所述的正向运动学数值求解方法，求得动平台实际的位姿t。将
所设计的lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，过程中有效利用了前述的运动学模型和动力学模型，从而获得运动的反馈信息和实际的位姿信息，通过轨迹跟踪的控制效果验证6-3-pus并联机构的运动学模型和动力学模型的正确性，以及lqr控制器的有效性。
[0113]
与前述的6-3-pus并联机构的轨迹跟踪控制方法的实施例相对应，本技术还提供了6-3-pus并联机构的轨迹跟踪控制装置的实施例。
[0114]
图5是根据一示例性实施例示出的一种6-3-pus并联机构的轨迹跟踪控制装置框图。参照图5，该装置应用于6-3-pus并联机构中，可以包括：
[0115]
建模模块21，用于建立6-3-pus并联机构的运动学模型和动力学模型；
[0116]
设计控制器模块22，用于选取状态变量，将所述动力学模型转化到线性状态空间，设计lqr控制器，其中所述控制器的输入为运动坐标误差和运动坐标时间微分的误差，输出为运动空间的力；
[0117]
求解模块23，用于将所述lqr控制器用于6-3-pus并联机构的轨迹跟踪控制，跟踪控制的输入为期望位姿td，跟踪控制的输出为实际位姿t，所述lqr控制器结合6-3-pus并联机构实际输出关节坐标q和关节速度通过所述运动学模型得到实际位姿t、实际的运动坐标ρ和实际的运动坐标时间微分将lqr控制器输出的运动空间的力f映射为关节的驱动力矩τ，控制6-3-pus并联机构执行运动，其中ρ和用作lqr控制器的反馈。
[0118]
关于上述实施例中的装置，其中各个模块执行操作的具体方式已经在有关该方法的实施例中进行了详细描述，此处将不做详细阐述说明。
[0119]
对于装置实施例而言，由于其基本对应于方法实施例，所以相关之处参见方法实施例的部分说明即可。以上所描述的装置实施例仅仅是示意性的，其中所述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物理单元，即可以位于一个地方，或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部模块来实现本技术方案的目的。本领域普通技术人员在不付出创造性劳动的情况下，即可以理解并实施。
[0120]
相应的，本技术还提供一种电子设备，包括：一个或多个处理器；存储器，用于存储一个或多个程序；当所述一个或多个程序被所述一个或多个处理器执行，使得所述一个或多个处理器实现如上述的6-3-pus并联机构的轨迹跟踪控制方法。
[0121]
相应的，本技术还提供一种计算机可读存储介质，其上存储有计算机指令，其特征在于，该指令被处理器执行时实现如上述的6-3-pus并联机构的轨迹跟踪控制方法。
[0122]
本领域技术人员在考虑说明书及实践这里公开的内容后，将容易想到本技术的其它实施方案。本技术旨在涵盖本技术的任何变型、用途或者适应性变化，这些变型、用途或者适应性变化遵循本技术的一般性原理并包括本技术未公开的本技术领域中的公知常识或惯用技术手段。说明书和实施例仅被视为示例性的，本技术的真正范围和精神由下面的权利要求指出。
[0123]
应当理解的是，本技术并不局限于上面已经描述并在附图中示出的精确结构，并且可以在不脱离其范围进行各种修改和改变。本技术的范围仅由所附的权利要求来限制。