地下结构的位移计算方法及装置与流程

本公开涉及地下结构抗震领域，特别涉及一种地下结构的位移计算方法。

背景技术：

地下结构在生活中随处可见，比如地下室、地下停车场或隧道等，这些地下结构的设计直接关系着人们的财产和生命安全，而在地下结构的设计过程中，地下结构的位移是主要考虑因素之一。

现有技术中，通过如下方法计算地下结构的位移：首先，计算地下结构周围土体的位移，将该地下结构周围土体的位移假定为是该地下结构的位移。

在实现上述功能的过程中，发明人发现现有技术至少存在如下缺陷：使用地下结构周围土体的位移代替地下结构的位移，只适应于周围土体刚度大于或者等于地下结构刚度的情况；然而，目前多数情况下周围土体刚度小于地下结构刚度，因此现有技术会过高地估计该地下结构的位移。导致计算得到的地下结构的位移有可能与真实的位移相去甚远。

技术实现要素：

为了解决相关技术中存在的问题，本公开提供一种地下结构的位移计算方法。所述技术方案如下：

根据本公开实施例的第一方面，提供一种地下结构的位移计算方法，该方法包括:

获取第一快速推算方程，所述第一快速推算方程用于指示地下结构的位移与预设范围内土体的土体位移参数的变化关系，所述土体位移参数用于指示所述土体的位移；

获取所述土体位移参数；

根据所述土体位移参数和所述第一快速推算方程计算所述地下结构的位移。

可选的，所述第一快速推算方程包括第二快速推算方程，所述第二快速推算方程用于指示在频域内所述地下结构的位移与所述土体位移参数的变化关系；所述土体位移参数包括所述土体位移的傅里叶幅值；

在获取第一快速推算方程之前还包括：

获取第三快速推算方程：[K_t]{u_t}＝[K₁]{u_b-u_t}，所述第三快速推算方程用于指示在时域内所述地下结构的位移与所述土体位移参数的变化关系，

其中，所述[K_t]为所述地下结构的刚度矩阵，所述{u_t}为所述地下结构的位移，所述[K₁]为所述土体的刚度矩阵，所述{u_b}为所述土体位移；

对所述第三快速推算方程进行傅里叶变换，得到所述第二快速推算方程：[K_t]{U_t(ω)}＝[K₁]{U_b(ω)-U_t(ω)}，

其中，所述U_t(ω)为所述地下结构的位移{u_t}的傅里叶幅值，所述U_b(ω)为所述土体位移{u_b}的傅里叶幅值。

可选的，在获取所述土体位移参数之前还包括：

获取质点-弹簧模型的第四快速推算方程：所述第四快速推算方程用于指示在时域内土质点位移与基岩入射加速度的变化关系，

其中，所述质点-弹簧模型包括n个所述土质点和n个与所述土质点对应的弹簧，所述质点-弹簧模型的形成方法包括：将所述土体沿所述地下结构的水平纵轴方向划分为n个土切片，每个所述土切片用一个土质点和一个弹簧组成的体系来等效，并通过所述弹簧将相邻的所述土质点连接，形成所述质点-弹簧模型，

其中，所述[M_s]为所述n个土质点的质量矩阵，{u_s}为所述土质点的位移，[C]为所述质点-弹簧模型在的时域内的阻尼矩阵，[K]为所述质点-弹簧模型的刚度矩阵，{ü_g}为所述基岩入射加速度；

对所述第四快速推算方程进行傅里叶变换，得到第五快速推算方程：

ω²i²[M_s]{U_s(ω)}e^iωt+ωi[C]{U_s(ω)}e^iωt+[K]{U_s(ω)}e^iωt＝-ω²i²[M_s]{U_g(ω)}e^iωt

其中，所述第五快速推算方程用于指示在频域内所述土质点与所述基岩入射加速度的变化关系，所述U_s(ω)为所述土质点的位移{u_s}的傅里叶幅值；

求解所述第五快速推算方程，得到所述土质点的位移{u_s}的傅里叶幅值U_s(ω)；

获取所述质点-弹簧模型的位移换算方程：{U_b(ω)}＝[α]{U_s(ω)}，所述位移换算方程用于指示所述土体位移{u_b}的傅里叶幅值U_b(ω)与所述土质点的位移{u_s}的傅里叶幅值U_b(ω)的变化关系，所述[α]为所述地下结构的振型与所述土质点的振型之比；

求解所述位移换算方程，得到所述土体位移{u_b}的傅里叶幅值U_b(ω)。

可选的，所述根据所述土体位移参数和所述第一快速推算方程计算所述地下结构的位移包括：

将所述土体位移的傅里叶幅值代入所述第一快速推算方程；

求解所述第一快速推算方程，得到所述地下结构的位移的傅里叶幅值；

对所述地下结构的位移的傅里叶幅值进行傅里叶逆变换得到所述地下结构的位移。

可选的，所述第五快速推算方程包括第六快速推算方程：-ω²[M_s]{U_s(ω)}+(1+2iξ)[K]{U_s(ω)}＝ω²[M_s]{U_g(ω)}，所述第六快速推算方程为所述质点-弹簧模型的阻尼模型为滞变阻尼模型时的动力平衡方程，当所述质点-弹簧模型的阻尼模型为滞变阻尼模型时，则有ωi[C]+[K]＝[K](1+2iξ)，将所述ωi[C]+[K]＝[K](1+2iξ)代入所述第五快速推算方程，得到所述第六快速推算方程。

根据本公开实施例的第二方面，提供一种地下结构的位移计算的装置，该装置包括：

第一获取模块，用于获取第一快速推算方程，所述第一快速推算方程用于指示地下结构的位移与预设范围内土体的土体位移参数的变化关系，所述土体位移参数用于指示所述土体的位移；

第二获取模块，用于获取所述土体位移参数；

计算模块，用于根据所述第二获取模块获取的所述土体位移参数和所述第一获取模块获取的所述第一快速推算方程所述计算所述地下结构的位移。

可选的，所述第一快速推算方程包括第二快速推算方程，所述第二快速推算方程用于指示在频域内所述地下结构的位移与所述土体位移参数的变化关系；所述土体位移参数包括所述土体位移的傅里叶幅值；

所述装置还包括：

第三获取模块，用于获取第三快速推算方程：[K_t]{u_t}＝[K₁]{u_b-u_t}，所述第三快速推算方程用于指示在时域内所述地下结构的位移与所述土体位移参数的变化关系，

其中，所述[K_t]为所述地下结构的刚度矩阵，所述{u_t}为所述地下结构的位移，所述[K₁]为所述土体的刚度矩阵，所述{u_b}为所述土体位移；

第一变换模块，用于对所述第三快速推算方程进行傅里叶变换，得到所述第二快速推算方程：[K_t]{U_t(ω)}＝[K₁]{U_b(ω)-U_t(ω)}，

其中，所述U_t(ω)为所述地下结构的位移{u_t}的傅里叶幅值，所述U_b(ω)为所述土体位移{u_b}的傅里叶幅值。

可选的，所述装置还包括：

第四获取模块，用于获取质点-弹簧模型的第四快速推算方程：所述第四快速推算方程用于指示在时域内土质点位移与基岩入射加速度的变化关系，

其中，所述质点-弹簧模型包括n个所述土质点和n个与所述土质点对应的弹簧，所述质点-弹簧模型的形成装置包括：将所述土体沿所述地下结构的水平纵轴方向划分为n个土切片，每个所述土切片用一个土质点和一个弹簧组成的体系来等效，并通过所述弹簧将相邻的所述土质点连接，形成所述质点-弹簧模型，

其中，所述[M_s]为所述n个土质点的质量矩阵，{u_s}为所述土质点的位移，[C]为所述质点-弹簧模型在的时域内的阻尼矩阵，[K]为所述质点-弹簧模型的刚度矩阵，{ü_g}为所述基岩入射加速度；

第二变换模块，用于对所述第四快速推算方程进行傅里叶变换，得到第五快速推算方程：

ω²i²[M_s]{U_s(ω)}e^iωt+ωi[C]{U_s(ω)}e^iωt+[K]{U_s(ω)}e^iωt＝-ω²i²[M_s]{U_g(ω)}e^iωt

其中，所述第五快速推算方程用于指示在频域内所述土质点与所述基岩入射加速度的变化关系，所述U_s(ω)为所述土质点的位移{u_s}的傅里叶幅值；

第一求解模块，用于求解所述第五快速推算方程，得到所述土质点的位移{u_s}的傅里叶幅值U_s(ω)；

获取所述质点-弹簧模型的位移换算方程：{U_b(ω)}＝[α]{U_s(ω)}，所述位移换算方程用于指示所述土体位移{u_b}的傅里叶幅值U_b(ω)与所述土质点的位移{u_s}的傅里叶幅值U_b(ω)的变化关系，所述[α]为所述地下结构的振型与所述土质点的振型之比；

第二求解模块，用于求解所述位移换算方程，得到所述土体位移{u_b}的傅里叶幅值U_b(ω)。

可选的，所述计算模块包括：

代入子模块，用于将所述土体位移的傅里叶幅值代入所述第一快速推算方程；

求解子模块，用于求解所述第一快速推算方程，得到所述地下结构的位移的傅里叶幅值；

变换子模块，用于对所述地下结构的位移的傅里叶幅值进行傅里叶逆变换得到所述地下结构的位移。

可选的，所述第五快速推算方程包括第六快速推算方程：-ω²[M_s]{U_s(ω)}+(1+2iξ)[K]{U_s(ω)}＝ω²[M_s]{U_g(ω)}，所述第六快速推算方程为所述质点-弹簧模型的阻尼模型为滞变阻尼模型时的动力平衡方程，当所述质点-弹簧模型的阻尼模型为滞变阻尼模型时，则有ωi[C]+[K]＝[K](1+2iξ)，将所述ωi[C]+[K]＝[K](1+2iξ)代入所述第五快速推算方程，得到所述第六快速推算方程。

本公开的实施例提供的技术方案可以包括以下有益效果：

通过获取第一快速推算方程和土体位移参数，根据该第一快速推算方程和该土体位移参数计算该地下结构的位移；由于该第一快速推算方程用于指示该地下结构的位移与预设范围内土体的土体位移参数的变化关系，所以通过该第一快速推算方程计算该地下结构的位移时，将该地下结构的刚度作为影响该地下结构位移的因素之一，从而提高了计算地下结构位移的广泛适用性和准确性。此外，在频域内进行求解可进一步实现该位移计算模型的快速推算。

应当理解的是，以上的一般描述和后文的细节描述仅是示例性的，并不能限制本公开。

附图说明

此处的附图被并入说明书中并构成本说明书的一部分，示出了符合本公开的实施例，并与说明书一起用于解释本公开的原理。

图1是根据一示例性实施例示出的一种地下结构的位移计算方法的流程图；

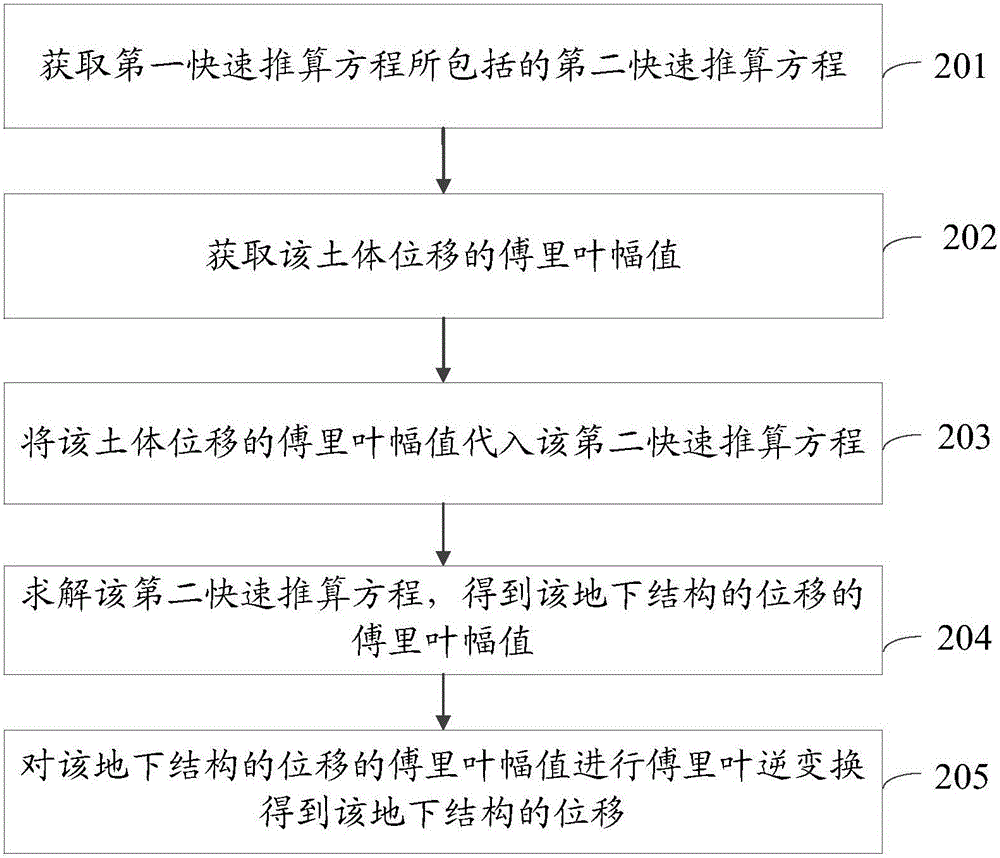
图2A是根据另一示例性实施例示出的一种地下结构的位移计算方法的流程图；

图2B是根据一示例性实施例示出的一种当地下结构受到沿该地下结构水平纵轴方向作用力时，将该地下结构简化为离散地下结构弹性地基梁的示意图；

图2C是根据另一示例性实施例示出的一种当地下结构受到沿该地下结构水平横轴方向(垂直该水平纵轴方向)作用力时，将该地下结构简化为离散地下结构弹性地基梁的示意图；

图2D是根据一示例性实施例示出的一种当地下结构受到沿该地下结构水平纵轴方向作用力时，该离散地下结构与该土体相互作用时的示意图；

图2E是根据另一示例性实施例示出的一种当地下结构受到沿该地下结构水平横轴方向(垂直水平纵轴方向)作用力时，该离散地下结构与该土体相互作用时的示意图；

图2F是根据一示例性实施例示出的一种质点-弹簧模型；

图2G是根据另一示例性实施例示出的一种质点-弹簧模型；

图2H是根据另一示例性实施例示出的一种确定弹簧刚度的示意图；

图2I是根据再一示例性实施例示出的一种确定弹簧刚度的示意图；

图3A是根据一示例性实施例示出的一种地下结构的位移计算装置的框图；

图3B是根据另一示例性实施例示出的一种地下结构的位移计算装置的框图；

图3C是根据一示例性实施例示出的一种计算地下结构的位移装置的框图。

具体实施方式

这里将详细地对示例性实施例进行说明，其示例表示在附图中。下面的描述涉及附图时，除非另有表示，不同附图中的相同数字表示相同或相似的要素。以下示例性实施例中所描述的实施方式并不代表与本公开相一致的所有实施方式。相反，它们仅是与如所附权利要求书中所详述的、本公开的一些方面相一致的例子。

图1是根据一示例性实施例示出的一种地下结构的位移计算方法的流程图，如图1所示，该地下结构的位移计算方法包括以下步骤：

在步骤101中，获取第一快速推算方程，该第一快速推算方程用于指示地下结构的位移与预设范围内土体的土体位移参数的变化关系，该土体位移参数用于指示该土体的位移。

在步骤102中，获取该土体位移参数。

在步骤103中，根据该土体位移参数和该第一快速推算方程计算该地下结构的位移。

综上所述，本公开实施例中提供的地下结构的位移计算方法，通过获取第一快速推算方程和土体位移参数，根据该第一快速推算方程和该土体位移参数计算该地下结构的位移；由于该第一快速推算方程用于指示该地下结构的位移与预设范围内土体的土体位移参数的变化关系，所以通过该第一快速推算方程计算该地下结构的位移时，将该地下结构的刚度作为影响该地下结构位移的因素之一，从而提高了计算地下结构的位移的准确性。

图2A是根据另一示例性实施例示出的一种地下结构的位移计算方法的流程图，如图2A所示，该地下结构的位移计算方法包括以下步骤：

在步骤201中，获取第一快速推算方程所包括的第二快速推算方程。

该第一快速推算方程用于指示地下结构的位移与预设范围内土体的土体位移参数的变化关系，该土体位移参数用于指示该土体的位移。该预设范围可以根据地下结构的实际情况进行确定，比如，如果该地下结构占用的空间较大时，可以确定一个较大的预设范围，当该地下结构占用的空间较小时，可以确定一个较小的预设范围。另外，该预设范围可以为距该地下结构预设距离所指示的范围。

该第二快速推算方程为该第一快速推算方程的一种，该第二快速推算方程用于指示在频域内该地下结构的位移与该土体位移参数的变化关系，则该土体位移参数包括该土体位移的傅里叶幅值。

为了在每次需要获取该第二快速推算方程时，可以直接从终端内获取到该第二快速推算方程，可预先确定该第二快速推算方程，并将确定的该动力平衡方程保存在该终端内。可选的，可通过如下方法确定该第二快速推算方程：

首先，获取第三快速推算方程：[K_t]{u_t}＝[K₁]{u_b-u_t}。然后，对获取到的该第三快速推算方程进行傅里叶变换，得到该第二快速推算方程：[K_t]{U_t(ω)}＝[K₁]{U_b(ω)-U_t(ω)}。

其中，该第三快速推算方程用于指示在时域内该地下结构的位移与该土体位移参数的变化关系。

其中，该[K_t]为该地下结构的刚度矩阵，该{u_t}为该地下结构的位移，该[K₁]为该土体的刚度矩阵，该{u_b}为该土体位移，该U_t(ω)为该地下结构的位移{u_t}的傅里叶幅值，该U_b(ω)为该土体位移{u_b}的傅里叶幅值。

可选的，该第三快速推算方程和该第二快速推算方程可以是基于如图2B或图2C所示的模型得到。参见图2B和图2C，图2B是根据一示例性实施例示出的一种当地下结构受到沿该地下结构水平纵轴方向作用力时，将该地下结构可以简化为离散地下结构弹性地基梁(图中21)的示意图。图2C是根据另一示例性实施例示出的一种当地下结构受到沿该地下结构水平横轴方向(垂直该水平纵轴方向)作用力时，将该地下结构可以简化为离散地下结构弹性地基梁的示意图。如图2B和图2C所示，将该地下结构简化为n个离散地下结构，该n个离散地下结构弹性地基梁通过离散地下结构接头(此处以弹簧为例)连接。另外，当该地下结构承受的力为沿该地下结构水平纵轴方向时，该离散地下结构弹性地基梁通过拉压弹簧(图中22)连接，当该地下结构承受的力为水平横轴方向(垂直该水平纵轴方向)时，将该离散地下结构弹性地基梁通过剪切或弯曲弹簧(图中23)连接。

另外，参见图2D和图2E，图2D是根据一示例性实施例示出的一种当地下结构受到沿该地下结构水平纵轴方向作用力时，该离散地下结构与该土体相互作用时的示意图。图2E是根据另一示例性实施例示出的一种当地下结构受到沿该地下结构水平横轴方向(垂直水平纵轴方向)作用力时，该离散地下结构与该土体相互作用时的示意图。图中l_k为该离散地下结构段中某一段的长度，k为离散地下结构段的序数，即k表示第k段离散地下结构。

其中，k₁为该土体与该离散地下结构相互作用时的弹簧刚度，n为离散地下结构的段数，k₁等于该地下结构对该土体的反作用力P与由该反作用力P所引起的该土体的位移δ的比值，即：

$k_1=\frac{P}{\mathrm{\δ}}$

此外，该土体的刚度矩阵[K₁]可以为与外部作用力无关的静刚度。

另外，该第三快速推算方程可以根据反应位移法原理得到，反应位移法原理为现在技术，在此不做详细说明。

在步骤202中，获取该土体位移的傅里叶幅值。

可选的，可通过如下方法获取该土体位移的傅里叶幅值：

第一，获取质点-弹簧模型的第四快速推算方程。

该质点-弹簧模型的第四快速推算方程为该第四快速推算方程用于指示在时域内土质点位移与基岩入射加速度的变化关系，其中，该[M_s]为n个土质点的质量矩阵，{u_s}为该土质点的位移，[C]为该质点-弹簧模型在的时域内的阻尼矩阵，[K]为该质点-弹簧模型的刚度矩阵，{ü_g}为基岩入射加速度。

具体的，为第i个该土质点的等效质量，n为该土质点的总个数；为三对角对称刚度矩阵，由质点-基岩模型中的质点-基岩弹簧刚度k₃与土质点之间的弹簧刚度k₂组成。

可选的，参见图2F，图2F是根据一示例性实施例示出的一种质点-弹簧模型。如图2F所示，该质点-弹簧模型包括n个该土质点和n个与该土质点对应的弹簧(图2F中以5个该土质点为例)，该质点-弹簧模型的形成方法包括：将该土体沿该地下结构的水平纵轴方向划分为n个土切片，每个该土切片用一个土质点和一个弹簧组成的体系来等效，并通过该弹簧将相邻的土质点进行连接，形成该质点-弹簧模型。

此外，参见图2G，图2G是根据另一示例性实施例示出的一种质点-弹簧模型。如图2G所示，该质点-弹簧模型还可以沿该地下结构水平横轴方向(垂直于该水平纵轴方向)划分为n个土切片(图2G中以5个土切片为例)，此时，该质点-弹簧模型的形成方法与图2F所示的质点-弹簧模型的形成方法相类似，在此不做详细描述。

另外，在得到该质点-弹簧模型时，可以通过如下方法确定该三对角对称刚度矩阵[K]：

[K]中三对角线上各元素的具体表达式为：

k₁₁＝k₃(1)+k₂(1)

k_i,i＝k₃(i)+k₂(i)+k₂(i-1)(i＝2,3,…,n-1)

k_n,n＝k₃(n)+k₂(n-1)

k_i,i-1＝-k₂(i-1)(i＝2,3,…,n)

式中，i为该土质点的编号；n为该土质点的总个数。

此外，可通过如下方法确定该土质点的等效质量m_i、质点-基岩弹簧刚度k₃和土质点之间的弹簧刚度k₂：

可以通过如下方法确定单位长度土切片等效质量m_e：

$m_e=\frac{{\left(\underset{i=1}{\overset{n}{\mathrm{\Σ}}}{m}_i{\mathrm{\φ}}_{i1}\right)}^2}{\underset{i=1}{\overset{n}{\Σ}}{m}_i{{\mathrm{\φ}}_{i1}}^2}$

式中，m_i为沿水平纵轴方向单位长度土切片沿深度第i层土的质量；n为单位长度土切片沿该土体深度的总层数；φ_i1为第i层土切片的第一阶振型。

则第k个土切片的等效质量m_k等于该单位长度土切片等效质量m_e与该第k个土切片长度l_k的乘积，即：

m_k＝m_el_k

质点-基岩弹簧刚度k₃为：

$k_3=m_k{\mathrm{\ω}}_1^2$

式中，ω₁为第k个土切片的第一阶固有频率。

此外，可以通过如下方法确定该质点-弹簧模型中土质点之间的弹簧刚度k₂：

参见图2H，图2H是根据另一示例性实施例示出的一种确定该弹簧刚度k₂的示意图。如图2H所示，当该质点-弹簧模型为如图2H所示的质点-弹簧模型时，该弹簧刚度k₂等于使相邻土质点产生单位相对位移需要的作用力。由振型分析可求出土体的第一阶振型位移δ_i，再由下式计算出产生单位相对位移所需的力，即：

$k_2=\frac{1}{l_k}\underset{i=1}{\overset{m}{\Σ}}{E}_i{A}_i{\mathrm{\δ}}_i$

式中，E_i、A_i分别为第i层土体的弹性模量和截面面积。

当该质点-弹簧模型为如图2I所示的质点-弹簧模型时，该弹簧刚度k₂的计算方法与当该质点-弹簧模型为如图2H所示的质点-弹簧模型时该弹簧刚度k₂计算方法相同，具体计算公式如下：

$k_2=\frac{1}{l_k}\underset{i=1}{\overset{m}{\Σ}}{G}_i{A}_i{\mathrm{\δ}}_i$

式中，G_i、A_i分别为第i层土体的剪切模量和截面面积。

另外，该质点-弹簧模型的第四快速推算方程是根据达朗贝原理建立的，通过达朗贝原理建立该质点-弹簧模型的第四快速推算方程为现在技术在此不做详细描述。

第二，对该第四快速推算方程进行傅里叶变换，得到第五快速推算方程。

对该第四快速推算方程进行傅里叶变换后，得到的第五快速推算方程为：ω²i²[M_s]{U_s(ω)}e^iωt+ωi[C]{U_s(ω)}e^iωt+[K]{U_s(ω)}e^iωt＝-ω²i²[M_s]{U_g(ω)}e^iωt。该第五快速推算方程用于指示在频域内该土质点与该基岩入射加速度的变化关系，该U_s(ω)为该土质点的位移{u_s}的傅里叶幅值。

可选的，该第五快速推算方程包括第六快速推算方程：-ω²[M_s]{U_s(ω)}+(1+2iξ)[K]{U_s(ω)}＝ω²[M_s]{U_g(ω)}，该第六快速推算方程为该质点-弹簧模型的阻尼模型为滞变阻尼模型时的动力平衡方程，当该质点-弹簧模型的阻尼模型为滞变阻尼模型时，则有ωi[C]+[K]＝[K](1+2iξ)，将该ωi[C]+[K]＝[K](1+2iξ)代入该第五快速推算方程，得到该第六快速推算方程。

通过将该质点-弹簧模型的阻尼模型为滞变阻尼模型，可以简化该第五快速推算方程，从而提高终端计算该地下结构的位移的效率。

第三，求解该第五快速推算方程，得到该土质点的位移{u_s}的傅里叶幅值U_s(ω)。

第四，获取该质点-弹簧模型的第一位移换算方程。

该质点-弹簧模型的第一位移换算方程为：{U_b(ω)}＝[α]{U_s(ω)}，该第一位移换算方程用于指示该土体位移{u_b}的傅里叶幅值U_b(ω)与该土质点的位移{u_s}的傅里叶幅值U_b(ω)的变化关系，该[α]为该地下结构的振型与该土质点的振型之比，具体的，其中，α_i为该地下结构的振型与第i个土质点的振型之比。

另外，该质点-弹簧模型的位移换算方程为现有公式在此不做详细描述。

在步骤2025中，求解该位移换算方程，得到该土体位移{u_b}的傅里叶幅值U_b(ω)。

可选的，为了提高终端计算该地下结构的位移的效率，可将该第五快速推算方程存储在该终端内，以使得在每次需要该第五快速推算方程时，可以直接从终端内获取到该第五快速推算方程，从而提高终端计算该地下结构的位移的效率。

在步骤203中，将该土体位移的傅里叶幅值代入该第二快速推算方程。

在步骤204中，求解该第二快速推算方程，得到该地下结构的位移的傅里叶幅值。

在步骤205中，对该地下结构的位移的傅里叶幅值进行傅里叶逆变换得到该地下结构的位移。

另外，需要说明的是，该地下结构的位移计算方法，也可在时域内进行，即，首先，获取该第三快速推算方程：[K_t]{u_t}＝[K₁]{u_b-u_t}；然后，获取该质点-弹簧模型的第四快速推算方程：求解该第四快速推算方程得到该土质点的位移{u_s}；然后，获取该质点-弹簧模型的第二位移换算方程：{u_b}＝[α]{u_s}，将该土质点的位移{u_s}代入该第二位移换算方程{u_b}＝[α]{u_s}中，求解该第二位移换算方程，得到该土体位移{u_b}；最后，将该土体位移代入该第三快速推算方程[K_t]{u_t}＝[K₁]{u_b-u_t}中，求解该第三快速推算方程[K_t]{u_t}＝[K₁]{u_b-u_t}得到该地下结构位移{u_t}。

此外，当得到该地下结构位移{u_t}后，可以根据该地下结构位移{u_t}求得该离散地下结构之间相互作用的内力和变形。有关如何根据该地下结构位移{u_t}求得该离散地下结构之间相互作用的内力和变形为现有技术，在此不做详细描述。

综上所述，本公开实施例中提供的地下结构的位移计算方法，通过获取第一快速推算方程和土体位移参数，根据该第一快速推算方程和该土体位移参数计算该地下结构的位移；由于该第一快速推算方程用于指示该地下结构的位移与预设范围内土体的土体位移参数的变化关系，所以通过该第一快速推算方程计算该地下结构的位移时，将该地下结构的刚度作为影响该地下结构位移的因素之一，从而提高了计算地下结构的位移的精度。

另外，本公开实施例中提供的地下结构的位移计算方法是在频域内进行的，与在时域内相比，提高了计算地下结构的位移的效率。

下述为本公开装置实施例，可以用于执行本公开方法实施例。对于本公开装置实施例中未披露的细节，请参照本公开方法实施例。

图3A是根据一示例性实施例示出的一种地下结构的位移计算装置的框图，如图3A所示，该地下结构的位移计算包括：第一获取模块301、第二获取模块302和计算模块303。

该第一获取模块301，用于获取第一快速推算方程，该第一快速推算方程用于指示地下结构的位移与预设范围内土体的土体位移参数的变化关系，该土体位移参数用于指示该土体的位移。

该第二获取模块302，用于获取该土体位移参数。

该计算模块303，用于根据该第二获取模块302获取的该土体位移参数和该第一获取模块301获取的该第一快速推算方程计算该地下结构的位移。

可选的，该第一快速推算方程包括第二快速推算方程，该第二快速推算方程用于指示在频域内该地下结构的位移与该土体位移参数的变化关系；该土体位移参数包括该土体位移的傅里叶幅值。

参见图3B，图3B是根据一示例性实施例示出的一种地下结构的位移计算装置的框图。如图3B所示，该装置还包括：第三获取模块304和第一变换模块305。

该第三获取模块304，用于获取第三快速推算方程：[K_t]{u_t}＝[K₁]{u_b-u_t}，该第三快速推算方程用于指示在时域内该地下结构的位移与该土体位移参数的变化关系。

其中，该[K_t]为该地下结构的刚度矩阵，该{u_t}为该地下结构的位移，该[K₁]为该土体的刚度矩阵，该{u_b}为该土体位移。

该第一变换模块305，用于对该第三快速推算方程进行傅里叶变换，得到该第二快速推算方程：[K_t]{U_t(ω)}＝[K₁]{U_b(ω)-U_t(ω)}。

其中，该U_t(ω)为该地下结构的位移{u_t}的傅里叶幅值，该U_b(ω)为该土体位移{u_b}的傅里叶幅值。

可选的，参见图3B，该装置还包括：第四获取模块306、第二变换模块307、第一求解模块308和第二求解模块309。

该第四获取模块306，用于获取质点-弹簧模型的第四快速推算方程：该第四快速推算方程用于指示在时域内土质点位移与基岩入射加速度的变化关系。

其中，该质点-弹簧模型包括n个该土质点和n个与该土质点对应的弹簧，该质点-弹簧模型的形成装置包括：将该土体沿该地下结构的水平纵轴方向划分为n个土切片，每个土切片用一个土质点和一个弹簧组成的体系来等效，并通过该弹簧将相邻的该土质点连接，形成该质点-弹簧模型。

其中，该[M_s]为该n个土质点的质量矩阵，{u_s}为该土质点的位移，[C]为该质点-弹簧模型在时域内的阻尼矩阵，[K]为该质点-弹簧模型的刚度矩阵，{ü_g}为该基岩入射加速度。

该第二变换模块307，用于对该第四快速推算方程进行傅里叶变换，得到第五快速推算方程：

ω²i²[M_s]{U_s(ω)}e^iωt+ωi[C]{U_s(ω)}e^iωt+[K]{U_s(ω)}e^iωt＝-ω²i²[M_s]{U_g(ω)}e^iωt

其中，该第五快速推算方程用于指示在频域内该土质点与该基岩入射加速度的变化关系，该U_s(ω)为该土质点的位移{u_s}的傅里叶幅值。

第一求解模块308，用于求解该第五快速推算方程，得到该土质点的位移{u_s}的傅里叶幅值U_s(ω)。

获取该质点-弹簧模型的位移换算方程：{U_b(ω)}＝[α]{U_s(ω)}，该位移换算方程用于指示该土体位移{u_b}的傅里叶幅值U_b(ω)与该土质点的位移{u_s}的傅里叶幅值U_b(ω)的变化关系，该[α]为该地下结构的振型与该土质点的振型之比。

该第二求解模块309，用于求解该位移换算方程，得到该土体位移{u_b}的傅里叶幅值U_b(ω)。

可选的，参见图3C，图3C是根据一示例性实施例示出的一种计算地下结构的位移装置的框图。如图3C所示，该计算模块303包括：代入子模块3031、求解子模块3032和变换子模块3033。

该代入子模块3031，用于将该土体位移的傅里叶幅值代入该第一快速推算方程。

该求解子模块3032，用于求解该第一快速推算方程，得到该地下结构的位移的傅里叶幅值。

该变换子模块3033，用于对该地下结构的位移的傅里叶幅值进行傅里叶逆变换得到该地下结构的位移。

可选的，该第五快速推算方程包括第六快速推算方程：-ω²[M_s]{U_s(ω)}+(1+2iξ)[K]{U_s(ω)}＝ω²[M_s]{U_g(ω)}，该第六快速推算方程为该质点-弹簧模型的阻尼模型为滞变阻尼模型时的动力平衡方程，当该质点-弹簧模型的阻尼模型为滞变阻尼模型时，则有ωi[C]+[K]＝[K](1+2iξ)，将该ωi[C]+[K]＝[K](1+2iξ)代入该第五快速推算方程，得到该第六快速推算方程。

综上所述，本公开实施例中提供的地下结构的位移计算装置，通过获取第一快速推算方程和土体位移参数，根据该第一快速推算方程和该土体位移参数计算该地下结构的位移；由于该第一快速推算方程用于指示该地下结构的位移与预设范围内土体的土体位移参数的变化关系，所以通过该第一快速推算方程计算该地下结构的位移时，将该地下结构的刚度作为影响该地下结构位移的因素之一，从而提高了计算地下结构的位移的精度。

另外，本公开实施例中提供的地下结构的位移计算装置，在频域内计算该地下结构的位移，与在时域内相比，提高了计算地下结构的位移的效率。

关于上述实施例中的装置，其中各个模块执行操作的具体方式已经在有关该方法的实施例中进行了详细描述，此处将不做详细阐述说明。

本领域技术人员在考虑说明书及实践这里公开的发明后，将容易想到本公开的其它实施方案。本申请旨在涵盖本公开的任何变型、用途或者适应性变化，这些变型、用途或者适应性变化遵循本公开的一般性原理并包括本公开未公开的本技术领域中的公知常识或惯用技术手段。说明书和实施例仅被视为示例性的，本公开的真正范围和精神由下面的权利要求指出。

应当理解的是，本公开并不局限于上面已经描述并在附图中示出的精确结构，并且可以在不脱离其范围进行各种修改和改变。本公开的范围仅由所附的权利要求来限制。