一种针灸力反馈形变模型的建模方法与流程

本发明涉及针灸模拟，尤其涉及一种针灸力反馈形变模型的建模方法。

背景技术：

针灸是传统中国养生治病的神奇医术，在现代养生医学中也有很广泛的应用。然而人体穴位比较难找，对于刚接触针灸的新手来说是一个很大的挑战，几乎无法实战练习，而扎错穴位也会对人体产生或大或小的影响，因此训练至关重要。传统的针灸培训成本高、风险高，虚拟针灸模拟系统可以帮助中医新手练习针灸，有效地解决这一问题。

柔性体表面形变是虚拟触觉交互过程的关键。常用的物理模型中，弹簧-质点模型具有建模简单、计算灵活、速度快的优点，但该模型精度有限，稳定性差。有限元模型精度高，但计算相对复杂。因此，具有良好的交互功能和形变效果的柔体模型对于虚拟手术系统来说至关重要。

技术实现要素：

本发明所要解决的技术问题是针对背景技术的不足，提供了一种针灸力反馈形变模型的建模方法。

本发明为解决上述技术问题采用以下技术方案：

一种针灸力反馈形变模型的建模方法，包含以下步骤：

步骤1)，重建软组织模型：采用体元模型重建软组织内部，采用网格模型重建软组织表皮；所述体元模型包含用于表示软组织内部的内部体元和用于表示模型针头的针体元；进行针灸模拟时，将模型针头在软组织内部所经过路径上的内部体元替换成针体元；

步骤2)，根据以下公式计算用于记录软组织模型的全局形变信息的的全局形变矩阵A：

其中，n是软组织模型的网格质点数，m_i是软组织模型中质点i的质量，i为大于等于1小于等于n的自然数，p_i是软组织模型中质点i的坐标，p_cm是形变后软组织模型的质心坐标，是质点i的初始坐标，是初始状态下软组织模型的质心坐标；

步骤3)，计算针刺点形变前的初始坐标和针刺点坐标p_c之间的距离

当且针尖坐标x与针刺点坐标p_c重合时，判定皮肤表层为未被刺破的状态，执行步骤4)，其中，d_max为预设的皮肤最大形变量；

当且针尖坐标x与针刺点坐标p_c不重合时，判定皮肤表层为被刺破的状态，执行步骤5)；

步骤4)，根据以下公式实时产生虚拟弹簧计算皮肤表层的力反馈F_out：

其中，σ(i)为软组织模型中受形变影响的网格质点集合,k为预设的虚拟弹簧系数，为软组织模型中质点i的初始坐标和当前坐标p_i之间的距离，N_out为以针尖为顶点沿针方向的单位向量；

步骤5)，根据针刺深度计算软组织模型的内部力反馈，同时对针刺后的皮肤进行复原控制：

步骤5.1)，根据针刺点坐标p_c和针尖坐标x的距离d_in计算软组织模型的内部力反馈F_in：

F_in＝ρ·d_in·N_in

其中，ρ是预设的的皮下组织密度，d_in是针刺点坐标p_c和针尖坐标x的距离，N_in是从针尖坐标x到针刺点坐标p_c的单位向量；

步骤5.2)，根据以下公式计算软组织模型中各个质点目标位置的坐标：

其中，为质点i目标位置的坐标，R是旋转矩阵，S是对称系数，矩阵A^T是矩阵A的转置矩阵；

步骤5.3)，根据以下公式优化软组织模型中各质点目标位置的坐标：

其中，η_i为预设的恢复系数，η_i∈[0,1]；

步骤5.4)，对于软组织模型中的各个质点i，控制其在预设的速率R_r下以η_i＝η_i-R_r的速度向其目标位置移动。

本发明可以在保证较好地表现针刺形变和恢复效果的前提下实现快速、逼真、实时的力反馈计算，与现有技术相比，具有以下技术效果：

1.使用体元和网格模型建模从而保证模型的稳定性，并且方便力反馈和形变的计算。

2.计算全局形变矩阵A以保证模型的全局稳定性，防止模型走样，并未之后的恢复算法做准备。

3.计算目标位置g_i实现皮肤被针刺破后的恢复，使针灸模型更为逼真。

4.插入恢复系数η_i以控制表面的恢复速率，进一步模拟真实情景下的针灸形变，保证形变恢复的稳定性和真实性。

5.由针头x和针刺点p_c之间的位置以及针刺点p_c和针刺点初始位置的距离为根据进行刺破判定，可以快速找到针头刺破皮肤的时间点，并以此为分割线进行表面形变的模拟和力反馈的模拟，逼真地展现在两种不同状态下的针灸模型。

6.未刺破前使用虚拟弹簧计算外部力反馈，使用虚拟弹簧计算力反馈方便快捷，计算时通过形变位置各顶点与其初始位置间的距离的改变，保证了力反馈的刷新。

7.刺破后考虑皮下组织密度，进行内部力反馈的计算，让模型的力反馈更为逼真，力反馈随针刺入的深度实时刷新，满足了系统的实时性。

附图说明

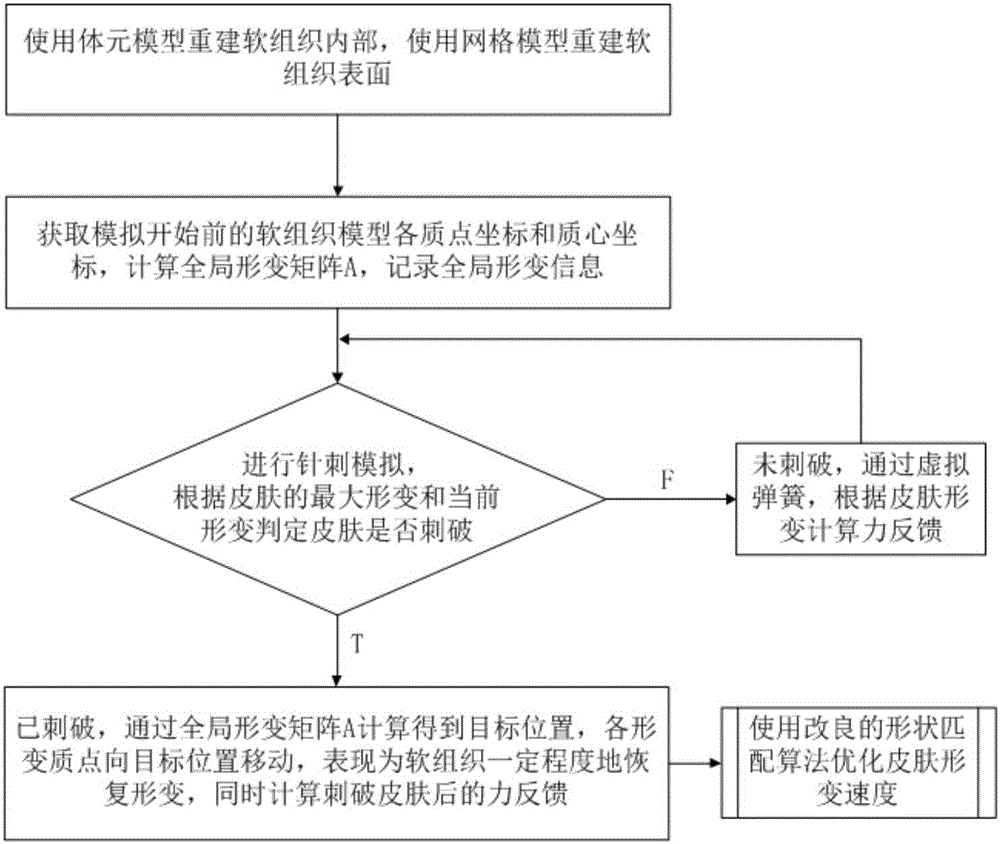
图1是针灸力反馈形变模型的仿真流程图；

图2是改良的形状匹配算法示例图；

图3是刺破前手臂横截面示例图；

图4是刺破后手臂横截面示例图。

具体实施方式

下面结合附图对本发明的技术方案做进一步的详细说明：

如图1所示，本发明公开了一种针灸力反馈形变模型的建模方法，包含以下步骤：

步骤1)，采用体元模型重建软组织内部，采用网格模型重建软组织表皮；所述体元模型包含用于表示软组织内部的内部体元和用于表示模型针头的针体元；进行针灸模拟时，将模型针头在软组织内部所经过路径上的内部体元替换成针体元。

步骤2)，计算全局形变矩阵A，全局形变矩阵A记录软组织的全局形变信息，也是形变恢复算法的基础，全局形变矩阵A需要获取软组织模型初始状态下的各质点坐标及质心坐标，在整个针灸模拟的过程中实时计算更新，根据以下公式计算软组织内部的全局形变矩阵A：

其中，n是软组织模型的网格质点数，m_i是软组织模型中质点i的质量，i为大于等于1小于等于n的自然数,p_i是软组织模型中质点i的坐标，p_cm是形变后软组织模型的质心坐标，是质点i的初始坐标，是初始状态下软组织模型的质心坐标。

步骤3)，进行刺破判定，计算针刺点形变前的初始坐标和针刺点坐标p_c之间的距离其中，d_max为预设的皮肤最大形变量；

当且针尖坐标x与针刺点坐标p_c重合时，视为皮肤表层未被刺破的状态，执行步骤4)；

当且针尖坐标x与针刺点坐标p_c不重合时，视为皮肤表层被刺破的状态，执行步骤5)。

步骤4)，皮肤未刺破，根据皮肤形变实时产生虚拟弹簧计算皮肤表层的力反馈，如图3所示，皮肤表层的力反馈F_out计算如下：

其中,σ(i)为软组织模型受形变影响的网格质点集合,k为预设的虚拟弹簧系数，为软组织模型中质点i初始坐标和当前坐标p_i之间的距离，N_out为以针尖为顶点沿针方向的单位向量。

步骤5)，皮肤已刺破，根据针刺深度计算软组织模型的内部力反馈，同时对针刺后的皮肤形变进行优化，使皮肤在刺破后一定程度地恢复原状，如图4所示。

步骤5.1)，计算软组织模型的内部接触力，通过针刺点坐标p_c和针尖坐标x的距离d_in的改变生成持续且变化的力反馈，内部力反馈F_in计算如下：

F_in＝ρ·d_in·N_in

其中，ρ是预设的皮下组织密度，d_in是针刺点坐标p_c和针尖坐标x的距离，N_in是从针尖坐标x到针刺点坐标p_c的单位向量。

计算刺破后的皮肤形变，当皮肤组织被刺破后，皮肤会一定程度地恢复形变，表现为各质点i向其对应的目标位置g_i移动，从而恢复初始形状，如图2所示。

步骤5.2)，目标位置g_i是皮肤形变恢复的关键，通过全局形变矩阵A求解目标位置g_i的坐标根据以下公式计算各质点的目标位置g_i的坐标

其中R是旋转矩阵，S是对称系数，R和S都是求解目标位置g_i的坐标所需要的重要参数，矩阵A^T是矩阵A的转置矩阵；

在实际操作时各质点对应的目标位置g_i位置固定，各质点i会快速回复形变，造成模拟的失真，为了防止软组织表面过快恢复，得到逼真的针灸形变效果，插入恢复系数η_i，η_i∈[0,1]，如图4所示，通过控制目标位置g_i随皮肤形变而移动，以控制各质点i恢复形变的速率，从而控制表面软组织的恢复速率。

步骤5.3)，根据以下公式优化软组织模型中各质点目标位置的坐标：

步骤5.4)，对于软组织模型中的各个质点i，控制其在预设的速率R_r下以η_i＝η_i-R_r的速度向其目标位置移动。

当η_i＝0时，质点i会直接移向目标位置g_i；当η_i＝1时，代表质点i不会立刻移动，i将在用户定义的速率R_r下逐渐以η_i＝η_i-R_r的速度向目标位置g_i移动。

本技术领域技术人员可以理解的是，除非另外定义，这里使用的所有术语(包括技术术语和科学术语)具有与本发明所属领域中的普通技术人员的一般理解相同的意义。还应该理解的是，诸如通用字典中定义的那些术语应该被理解为具有与现有技术的上下文中的意义一致的意义，并且除非像这里一样定义，不会用理想化或过于正式的含义来解释。

以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。