一种基于图论的车辆轨迹聚类方法与流程

本发明涉及车联网和计算领域，特别是一种基于图论的车辆轨迹聚类方法。

背景技术

随着车辆行业应用系统规模的迅速扩大，车载应用所产生的数据呈爆炸性增长，智能交通系统在数据的采集、处理、分析、利用等方面面临着巨大的挑战。在信息技术和云计算快速发展的背景下，车联网的概念逐渐被人们熟悉。车联网作为物联网的一个典型应用，使精细化采集道路网上运行车辆的时空信息成为可能，从而实现了对交通的更加智能化的管理。

数据分析技术中的聚类分析方法是研究和分析交通热点数据的有效方法。聚类分析是指将物理或抽象对象的集合分组由类似的对象组成的多个类的分析过程，在基于聚类分析得到的交通规律的基础上，再对其进行相应的分析，就可预测出该城市的交通规律。

传统聚类方法如dbscan、gmm算法在样本量较大时，要获得聚类结论有一定困难。由于相对系数是根据数据集的内在结构反映来建立反映数据间的内在联系的指标，而实践中尽管所得出的数据中发现他们之间有紧密的关系，但事物之间却无任何内在联系，此时，如果根据相似系数得出聚类分析的结果，显然是不适当的，但是，传统聚类分析模型本身却无法识别这类错误。

技术实现要素：

有鉴于此，本发明的目的是提出一种基于图论的车辆轨迹聚类方法，能够有效提高数据处理的速度与质量。

本发明采用以下方案实现：一种基于图论的车辆轨迹聚类方法，包括以下步骤：

步骤s1：获取车联网数据，利用spark平台将海量车辆轨迹数据进行数据清洗；

步骤s2：将坐标点投射到地图上，通过坐标点的位置相对距离关系根据所设定的k值以及相对近似性形成连通图，再利用互连性，将聚簇之间的连接性强度大于预设值的聚簇进行合并；

步骤s3：采用真实出租车轨迹数据进行分析，得到不同时间段、不同区域的车流量，即给出最优打车方案。

进一步地，步骤s1中，车联网数据中的车辆轨迹数据是指时空环境下，通过对一个或多个移动对象运动过程的采样所获得的数据信息，包括数据点的地理位置、运动时间、速度等，反映了移动对象某一时间段的行动状况。获取的车联网数据为真实城市出租车数据，数据类型包括车牌、消息来源、上车时间、下车时间、上车经度和纬度、下车经度和纬度。

进一步地，步骤s1中，所述数据清洗具体包括：

去除经纬度超出预设范围数据：本发明研究受经纬度数据限制，剔除所研究城市坐标位置外的数据；

去除重复数据：若行车过程出现堵车，司机重复打表或者车辆某一时刻静止，则会导致数据重复，对此类数据进行判断并去除；

去除时间异常数据：打车数据采集间隔错误，若车载数据收集装置出现故障，建筑物体遮挡导致接受延迟等，致使乘客上车时间与下车时间不符合实际，这类数据也要进行清除；

清除格式异常数据：由于处理的数据量相对比较庞大，不可避免会出现各种各样的错误，例如，车辆坐标缺失，车辆时间缺失，对出现的这类型错误的数据要直接剔除。

进一步地，步骤s2具体包括以下步骤：

k邻近算法能够将样本集按邻近关系分解成组，对于海量的数据，k邻近算法能够有效的对数据集进行分类，当数据量变多时，欧式距离的区分能力较差，本发明提出k邻近连通图，利用余弦距离来进行判定来解决该问题。k近邻有向图利用knn算法构造有向图knn＝(q，p)，假设q＝{q1，q2，...，qn}，p＝{p1，p2，...，pm}，其中q，p是两个对象项，各自具有n个长度的特征值，在这里，定义x和y的相似度为：f(x，y)。

步骤s21：设定k值，在二维空间中，利用数据之间的相对近似性，通过对象a(q1，p1)与对象b(q2，p2)的夹角余弦来判断结点之间的相近关系；

步骤s22：利用聚簇之间的互连性，将部分聚簇进行合并，得到新的分类结果。

进一步地，步骤s22具体包括以下步骤：

步骤s221：计算对象a(q1，p1)与对象b(q2，p2)的夹角余弦：

夹角余弦值越接近1说明对象a(q1，p1)与对象b(q2，p2)之间的相似性越高，由此形成连通图；其中，最终的余弦距离在[-1,1]之间，当两个对象越相似时，说明余弦角越小越接近1值，当两个对象的相似度越低时，余弦的角越大，值越接近-1。k近邻有向图描述了结点之间的相近关系。接着，考虑聚簇的近似性与互连性来合并聚簇；

步骤s222：采用下式计算相对近似性rc：

式中，是连接簇ci与簇cj平均权值；是簇ci边的平均权值，是簇cj边的平均权值；

步骤s223：采用下式计算相对互连性ri：

式中，ec(ci,cj)是连接簇ci与cj(k-邻近图)的边之和，ec(ci)表示ci聚簇内的边的权重和，ec(cj)表示cj聚簇内的边的权重和；

进一步包括步骤s223：基于图论的聚类算法兼具互连性和近似性，通过一个度量函数来表示两个簇之间的相似度：

function＝ri(ci,cj)×rc(ci,cj)α；

式中，在算法中定义了相对互连性ri，相对近似性rc，ci、cj表示的是第i个、第j个聚簇内的数据点的个数。α是指定参数，通常大于1。通过该步骤利用相似性与互连性对聚簇进行进一步的划分，得到更为精确的分类结果。

基于点的起点-目的地的方法依据每个点都是高度精确的gps位置，每个轨迹都是从一个位置移动到另外一个位置，即起点指向目的地点，真实的数据集可能有数百万个点，并且是移动点。首先，每个位置是空间中独立的采样点，通常不与其他点重叠。例如车辆到达相同地点会采取不同的gps点。其次，从大规模运动中提取结构是具有一定困难的，即点对点流量，数百万的点数和流量，致使数据通过直接映射点和轨迹是不切实际的，分析应该是能够合成大量流动点数，提取主要结构模式。聚合位置(例如数百万个gps点)具有足够大小的空间集群(区域)，通过点与点之间的互连性对它们进行k邻近聚类，结果可能代表有意义的地方。再利用簇与簇的近似性对聚簇结果进行合并，将空间和时间上的测量结果可视化，可以清晰的观察具有位置特征的时空模式。

进一步地，步骤s3具体包括以下步骤：

步骤s31：采用数据为不同时刻的车流量图，分析每小时车辆运行数量，通过每小时打车数量的波动来直观的反应出城市打车的高峰期；

步骤s32：采用热力图来展现市区各个地段车流量的密集程度，直观的观察出交通流热点区域。

与现有技术相比，本发明有以下有益效果：本发明提出了一种分析基于点的起点-终点轨迹的新方法，利用该方法，可以发现车流量分布的时空模式，如位置特征和时空中的运动趋势，根据本发明图论聚类结果与真实城市道路分布进行比较，实际结果基本符合实际城市路况，并给出辅助城市建设方案。

附图说明

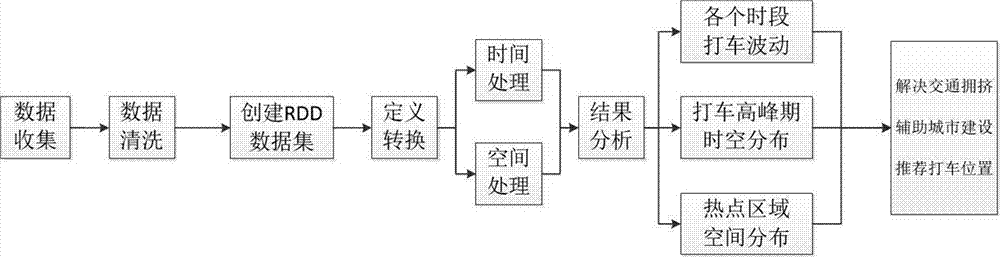
图1为本发明实施例的方法流程示意图。

图2为本发明实施例的不同时刻打车数量示意图。

图3为本发明实施例的图论聚类实验结果示意图。

具体实施方式

下面结合附图及实施例对本发明做进一步说明。

应该指出，以下详细说明都是例示性的，旨在对本申请提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

如图1所示，本实施例提供了一种基于图论的车辆轨迹聚类方法，包括以下步骤：

步骤s1：获取车联网数据，利用spark平台将海量车辆轨迹数据进行数据清洗；在本实例中，采用spark分布式框架搭建分布式集群，部署了一个master节点和多个worker节点构成集群进行分布式计算，以解决海量数据计算问题。

步骤s2：将坐标点投射到地图上，通过坐标点的位置相对距离关系根据所设定的k值以及相对近似性形成连通图，再利用互连性，将聚簇之间的连接性强度大于预设值的聚簇进行合并；

步骤s3：采用真实出租车轨迹数据进行分析，得到不同时间段、不同区域的车流量，即给出最优打车方案。

在本实施例中，步骤s1中，车联网数据中的车辆轨迹数据是指时空环境下，通过对一个或多个移动对象运动过程的采样所获得的数据信息，包括数据点的地理位置、运动时间、速度等，反映了移动对象某一时间段的行动状况。获取的车联网数据为真实城市出租车数据，数据类型包括车牌、消息来源、上车时间、下车时间、上车经度和纬度、下车经度和纬度。

在本实施例中，步骤s1中，所述数据清洗具体包括：

去除经纬度超出预设范围数据：本发明研究受经纬度数据限制，剔除所研究城市坐标位置外的数据；

去除重复数据：若行车过程出现堵车，司机重复打表或者车辆某一时刻静止，则会导致数据重复，对此类数据进行判断并去除；

去除时间异常数据：打车数据采集间隔错误，若车载数据收集装置出现故障，建筑物体遮挡导致接受延迟等，致使乘客上车时间与下车时间不符合实际，这类数据也要进行清除；

清除格式异常数据：由于处理的数据量相对比较庞大，不可避免会出现各种各样的错误，例如，车辆坐标缺失，车辆时间缺失，对出现的这类型错误的数据要直接剔除。

在本实施例中，步骤s2具体包括以下步骤：

k邻近算法能够将样本集按邻近关系分解成组，对于海量的数据，k邻近算法能够有效的对数据集进行分类，当数据量变多时，欧式距离的区分能力较差，本发明提出k邻近连通图，利用余弦距离来进行判定来解决该问题。k近邻有向图利用knn算法构造有向图knn＝(q，p)，假设q＝{q1，q2，...，qn}，p＝{p1，p2，...，pm}，其中q，p是两个对象项，各自具有n个长度的特征值，在这里，定义x和y的相似度为：f(x，y)。

步骤s21：设定k值，在二维空间中，利用数据之间的相对近似性，通过对象a(q1，p1)与对象b(q2，p2)的夹角余弦来判断结点之间的相近关系；

步骤s22：利用聚簇之间的互连性，将部分聚簇进行合并，得到新的分类结果。

在本实施例中，步骤s22具体包括以下步骤：

步骤s221：计算对象a(q1，p1)与对象b(q2，p2)的夹角余弦：

夹角余弦值越接近1说明对象a(q1，p1)与对象b(q2，p2)之间的相似性越高，由此形成连通图；其中，最终的余弦距离在[-1,1]之间，当两个对象越相似时，说明余弦角越小越接近1值，当两个对象的相似度越低时，余弦的角越大，值越接近-1。k近邻有向图描述了结点之间的相近关系。接着，考虑聚簇的近似性与互连性来合并聚簇；

步骤s222：采用下式计算相对近似性rc：

式中，是连接簇ci与簇cj平均权值；是簇ci边的平均权值，是簇cj边的平均权值；

步骤s223：采用下式计算相对互连性ri：

式中，ec(ci,cj)是连接簇ci与cj(k-邻近图)的边之和，ec(ci)表示ci聚簇内的边的权重和，ec(cj)表示cj聚簇内的边的权重和；

在本实施例中，进一步包括步骤s223：基于图论的聚类算法兼具互连性和近似性，通过一个度量函数来表示两个簇之间的相似度：

function＝ri(ci,cj)×rc(ci,cj)α；

式中，在算法中定义了相对互连性ri，相对近似性rc，ci、cj表示的是第i个、第j个聚簇内的数据点的个数。α是指定参数，通常大于1。

基于点的起点-目的地的方法依据每个点都是高度精确的gps位置，每个轨迹都是从一个位置移动到另外一个位置，即起点指向目的地点，真实的数据集可能有数百万个点，并且是移动点。首先，每个位置是空间中独立的采样点，通常不与其他点重叠。例如车辆到达相同地点会采取不同的gps点。其次，从大规模运动中提取结构是具有一定困难的，即点对点流量，数百万的点数和流量，致使数据通过直接映射点和轨迹是不切实际的，分析应该是能够合成大量流动点数，提取主要结构模式。聚合位置(例如数百万个gps点)具有足够大小的空间集群(区域)，通过点与点之间的互连性对它们进行k邻近聚类，结果可能代表有意义的地方。再利用簇与簇的近似性对聚簇结果进行合并，将空间和时间上的测量结果可视化，可以清晰的观察具有位置特征的时空模式。

在本实施例中，步骤s3具体包括以下步骤：

步骤s31：采用数据为不同时刻的车流量图，分析每小时车辆运行数量，通过每小时打车数量的波动来直观的反应出城市打车的高峰期；

步骤s32：采用热力图来展现市区各个地段车流量的密集程度，直观的观察出交通流热点区域。

具体的，在本实施例中，采用不同时刻的车辆数量来反应打车波动程度，如图2所示，可以通过每小时车辆的数量清晰的观察到各个时刻的打车波动。本实例采用热力图来展现成都市各个地段车流量的密集程度，在地图上可以明显区分哪个地段车辆密集程度较高，直观的观察出交通流热点区域。最后，利用spark大数据处理平台实现图论聚类算法，在考虑gps偏移等条件下，聚类的效果还是比较合理的，可以发现大致将成都市出租车运营地区划分为几个区域。如图3所示。

以上所述仅为本发明的较佳实施例，凡依本发明申请专利范围所做的均等变化与修饰，皆应属本发明的涵盖范围。